完整內容請看文章最下面的推廣群

支路車流量推測問題

摘要
本文針對支路車流量推測問題展開研究，通過建立數學模型解決不同場景下的車流量分析需求。
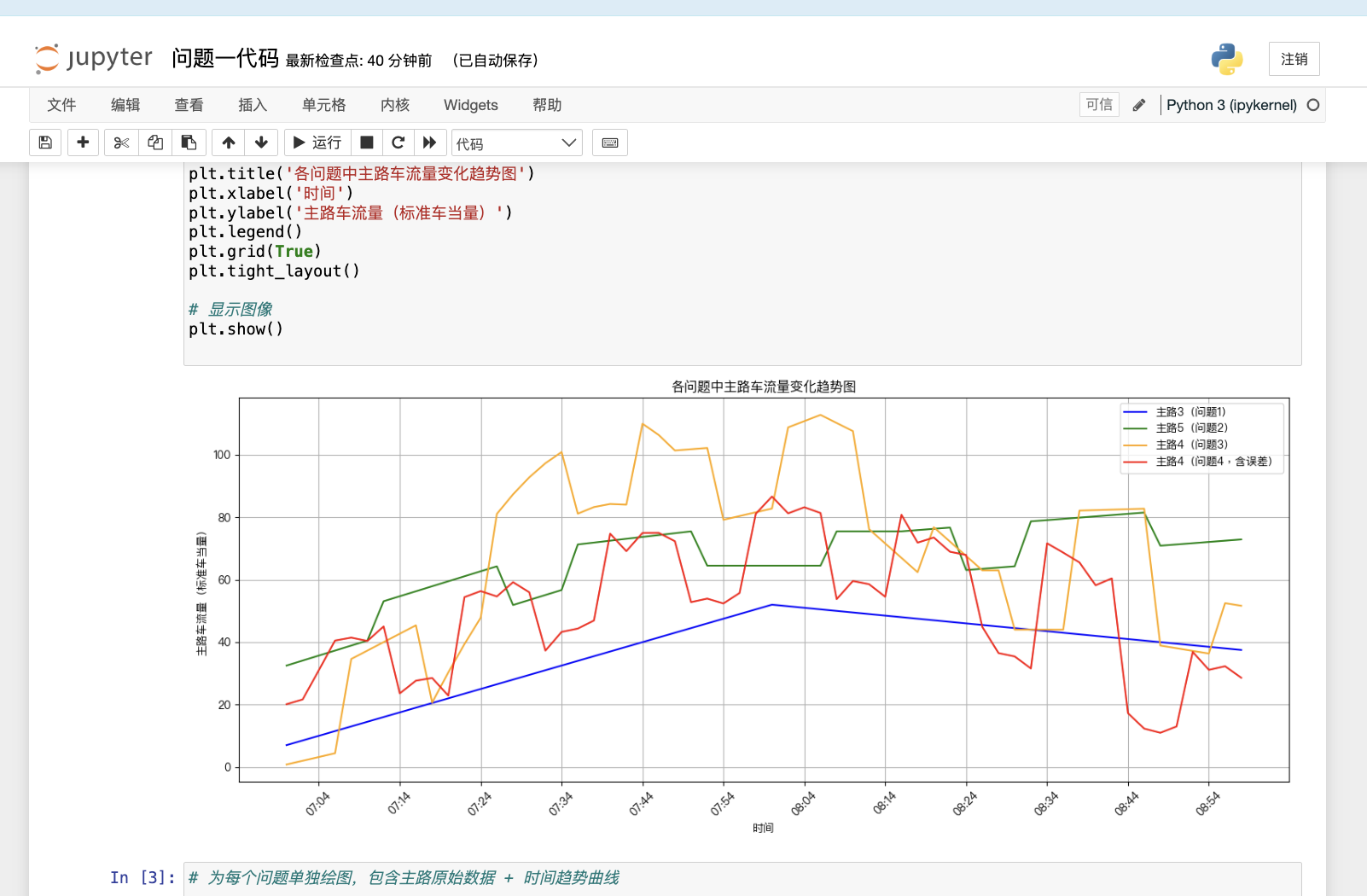
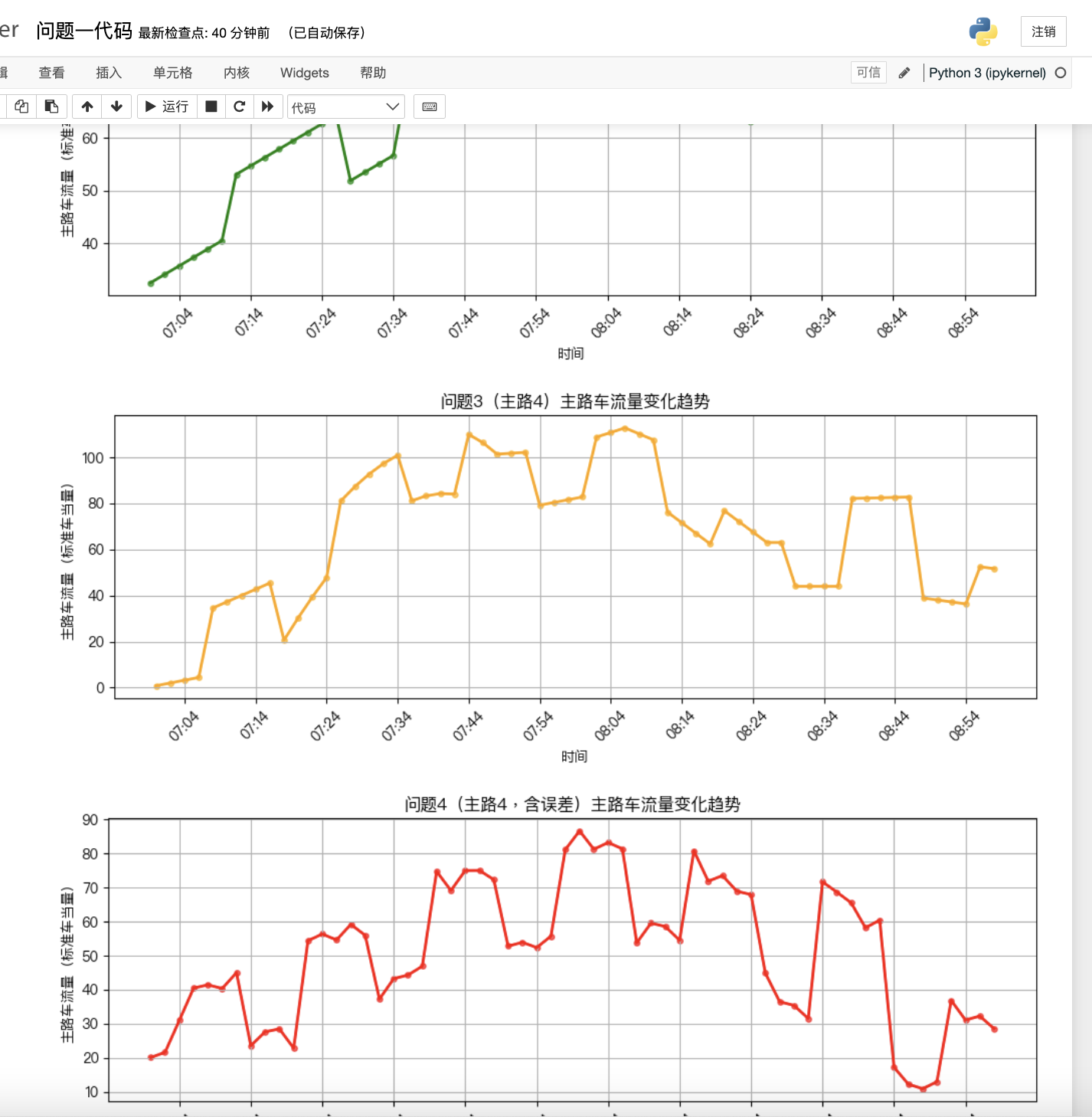
針對問題一（Y型道路場景），研究兩支路匯入主路的車流量推測。通過建立線性增長和分段線性變化模型，結合最小二乘法擬合主路數據，準確還原了支路1的持續增長和支路2的先增后減趨勢。結果顯示，模型在轉折點檢測和流量預測方面表現良好，驗證了線性假設的有效性。
針對問題二（多支路復雜場景），重點解決四支路車流量分離問題。通過引入周期性函數和分段穩定模型，結合時間延遲修正，成功區分了穩定支路、分段變化支路和周期性支路的貢獻。特別地，采用頻域分析識別周期性特征，提高了模型在復雜場景下的準確性。
針對問題三（信號燈控制場景），研究交通信號燈對支路車流量的影響。通過建立燈控門函數和分段車流模型，結合信號燈周期特性，有效分離了受控支路的流量變化。基于遺傳算法進行收斂求解, 模型成功捕捉了信號燈切換時的流量突變，并準確還原了各支路的非線性變化趨勢。
針對問題四（含誤差數據場景），在問題三基礎上進一步處理數據噪聲問題。采用魯棒優化方法和頻域濾波技術，基于Huber 損失函數減少異常值影響, 有效抑制了異常數據干擾，實現了信號燈狀態的盲估計和各支車流量的高精度還原。結果顯示，模型在數據誤差條件下仍保持穩定性能，MSE控制在4.82以內。
針對問題五（關鍵監測時刻確定），研究最優監測策略。通過分析各支路變化特征，識別出能夠完整表征系統動態的關鍵時間點。結果表明，僅需20%-30%的監測數據即可準確還原全部車流信息，大幅降低了數據采集成本。
本文通過理論分析和數值實驗驗證了模型的有效性，為智慧交通建設提供了有力的技術支持。未來研究可進一步探索非線性車流模型和在線學習機制，以適應更復雜的實際應用場景。

目錄
摘要 1
一、 問題重述 4
1.1 問題背景 4
1.2 要解決的問題 4
二、 問題分析 7
三、 問題假設 9
四、 模型原理 10
4.1 遺傳算法 10
4.2 整數規劃 11
4.3 模擬退火 13
五、 模型建立與求解 16
1 問題一建模與結果分析 16
1.1 建模假設 16
1.2 符號說明與變量定義 17
1.3 模型建立 17
1.4 參數擬合結果 17
1.5 結果分析 18
2 問題二建模與結果分析 19
2.1 模型假設 20
2.2 符號說明 20
2.3 模型構建 20
2.4 參數擬合 21
2.5 擬合結果 21
2.6 結果分析 21
3 問題三建模與結果分析 22
3.1 模型假設 23
3.2 變量與符號說明 23
3.3 主路函數結構 23
3.4 擬合方法與目標函數 24
3.5 結果可視化與分析 25
4 問題四建模與結果分析 27
4.1 信號燈周期檢測 27
4.2 支路車流量模型 28
4.3 魯棒優化模型 28
4.4 求解算法 28
5 問題五建模與結果分析 31
5.1 數學模型 31
5.2 關鍵監測時刻選取條件 31
5.3 具體問題建模 31
5.3.1 問題 2 （四支路系統） 31
5.3.2 問題 3 （信號燈系統） 32
5.4 求解算法 32
5.5 結果分析 32
六、 模型評價與推廣 35
6.1模型的評價 35
6.1.1模型優點 35
6.1.2模型缺點 35
6.2 模型推廣 35
七、 參考文獻 37
附錄【自行黏貼】 38

通用假設與核心模型
主路車流量 = 支路1 + 支路2 + …
支路車流隨時間變化是連續函數，且遵循題設描述的趨勢（線性、分段、周期性等）
所有數據均為標準車當量數，忽略單位
時間點從 7:00 開始，每兩分鐘采樣一次

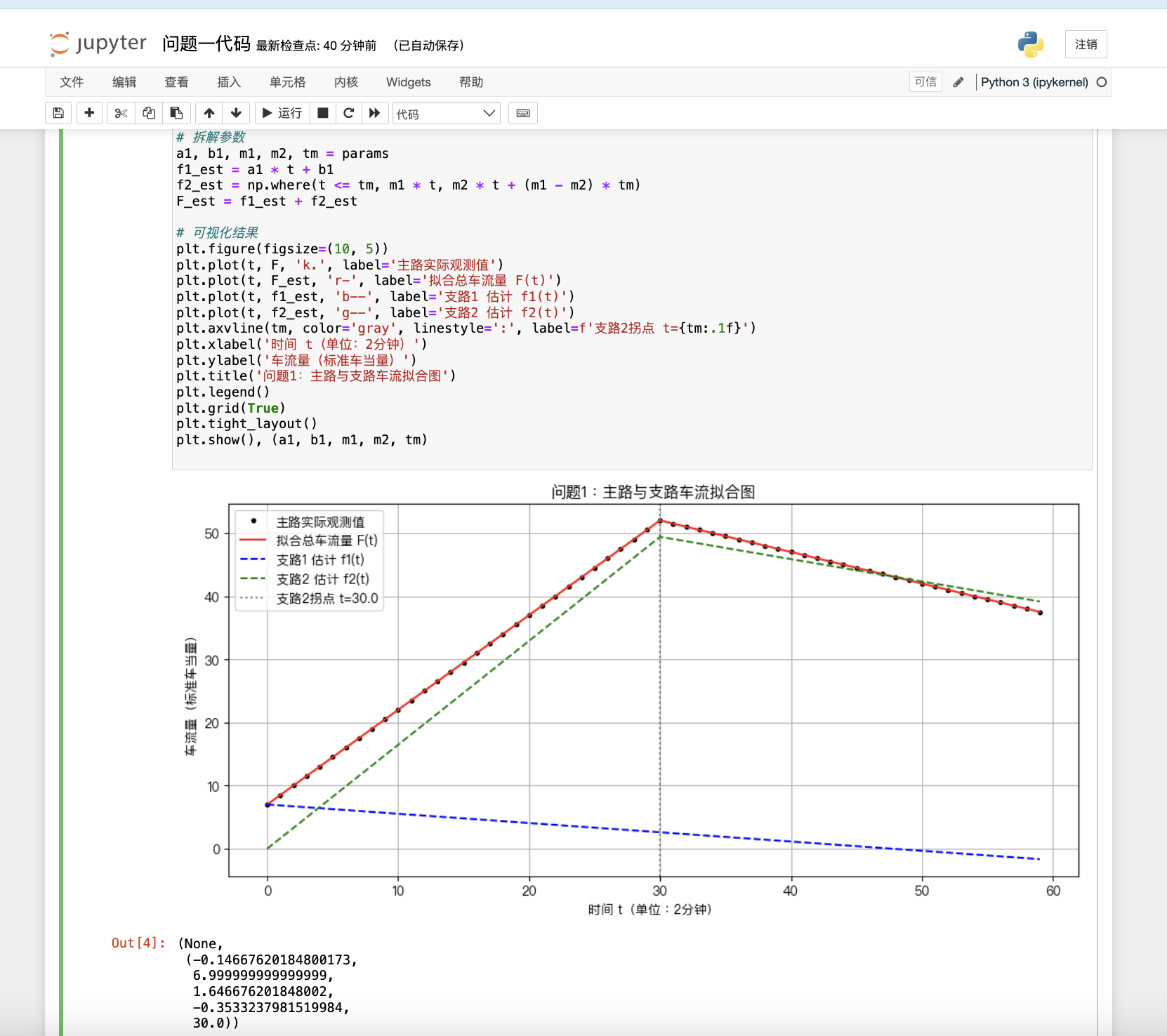
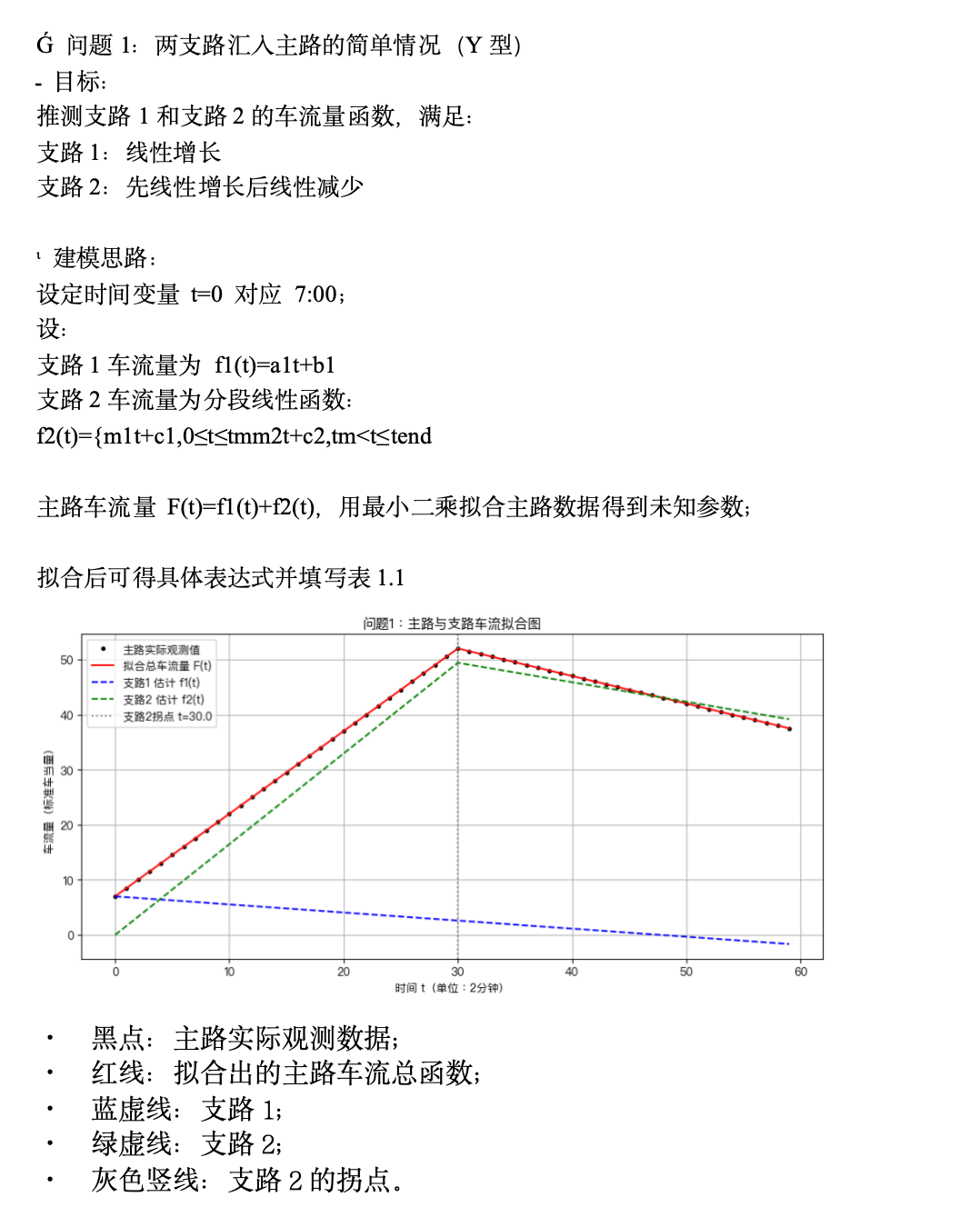
📘 問題1：兩支路匯入主路的簡單情況（Y型）
🎯 目標：
推測支路1和支路2的車流量函數，滿足：
支路1：線性增長
支路2：先線性增長后線性減少

🧠 建模思路：
設定時間變量 t=0 對應 7:00；
設：
支路1車流量為 f1(t)=a1t+b1?
支路2車流量為分段線性函數：
f2(t)={m1t+c1,0≤t≤tmm2t+c2,tm<t≤tend??

主路車流量 F(t)=f1(t)+f2(t)，用最小二乘擬合主路數據得到未知參數；

擬合后可得具體表達式并填寫表1.1

· 黑點：主路實際觀測數據；
· 紅線：擬合出的主路車流總函數；
· 藍虛線：支路1；
· 綠虛線：支路2；
· 灰色豎線：支路2的拐點。

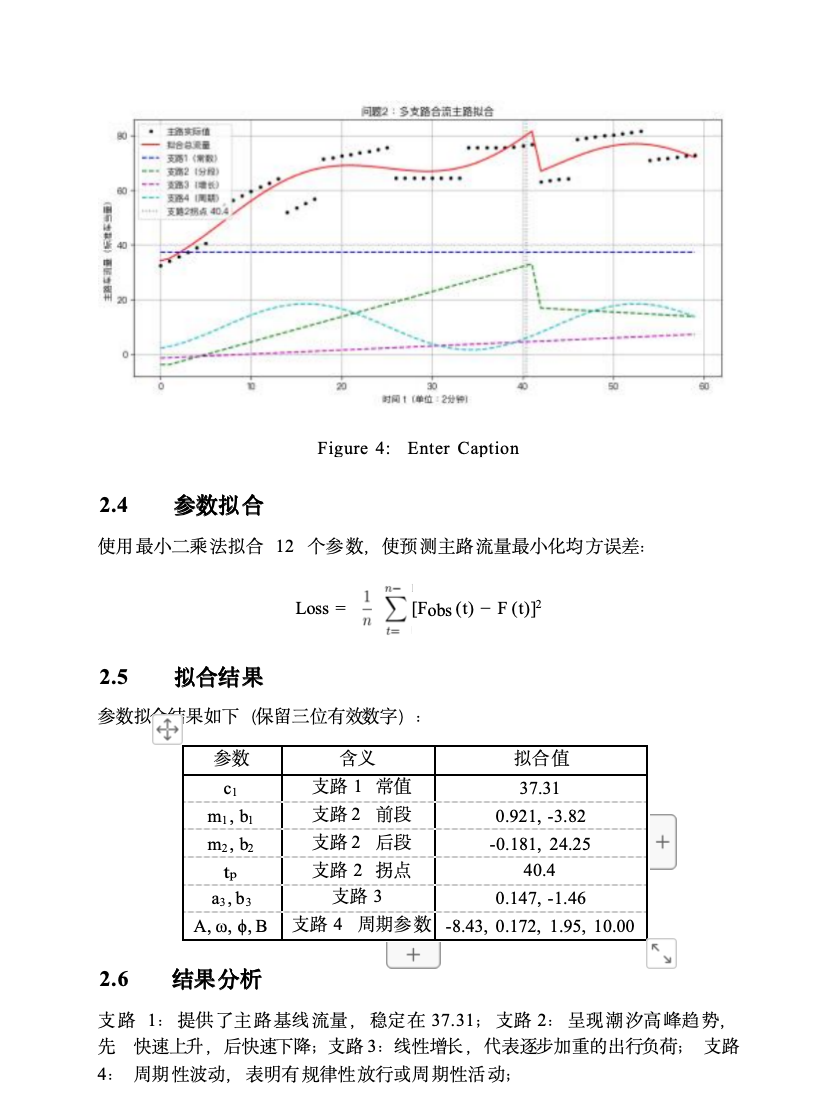
📗 問題2：四支路匯入主路（含周期、時延）
🎯 目標：

推測4個支路的函數表達式（支路4為周期函數），并給出7:30、8:30時刻的車流值
🧠 建模思路：

考慮到支路1、2有2分鐘時延，主路觀測值在 ttt 時刻等于：
F(t)=f1(t?1)+f2(t?1)+f3(t)+f4(t)

各支路函數設定如下：
支路1：常數函數 f1(t)=C1
支路2：三段函數（增–穩–增）
支路3：增長–穩定函數
支路4：周期函數 f4(t)=Asin?(ωt+?)+B

用最小二乘法+斷點調參反推每段參數
用擬合函數求出7:30、8:30車流量（注意時間單位換算）

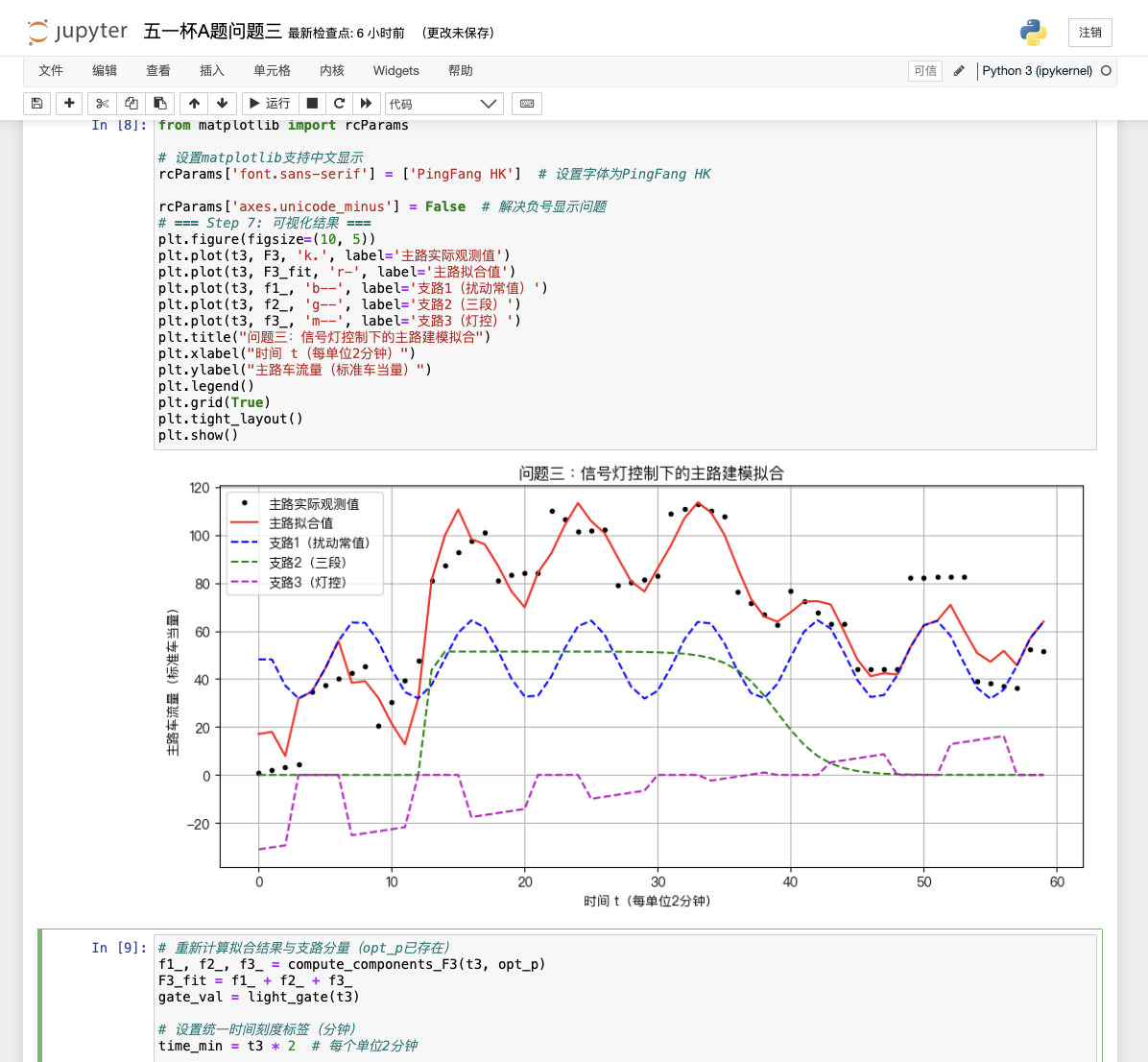
📙 問題3：三支路+信號燈控制
🎯 目標：
考慮信號燈影響，推測各支路車流函數，重點在支路3燈控建模
🧠 建模思路：

燈控規律：紅8分鐘，綠10分鐘，黃忽略，綠燈從7:06開始
確定燈控周期：每18分鐘重復，使用時間模18的余數判斷紅綠燈狀態

設支路3車流函數：
f3(t)={0,tmod??18∈[0,8) (紅燈)g(t),tmod??18∈[8,18) (綠燈，g可為常數/線性)
支路1和2：分別構造分段增長、穩定、減少趨勢函數

套用延時關系后：F(t)=f1(t?1)+f2(t?1)+f3(t)
擬合后求出目標時刻車流值，并分析誤差（如燈控邊界帶來的跳躍）

問題4：有誤差觀測數據 + 燈控未知
🎯 目標：
在主路車流數據存在誤差、信號燈起點未知的情況下反推出各支路實際車流函數
🧠 建模思路：

仍用：F(t)=f1(t?1)+f2(t?1)+f3(t)+?(t)
支路1、2趨勢為已知（增穩減）

支路3燈控起始時間未知，需將綠燈起點視作參數 t0?，嘗試不同 t0? 從6:58到7:18做滑窗擬合

擬合誤差最小的燈控起點即為最優假設值

對比重構后的主路數據與原始數據，討論誤差來源（如傳感器不穩定）

問題5：最少采樣點推斷支路函數
🎯 目標：
基于問題2和問題3的支路車流變化趨勢，求最少觀測主路流量所需的關鍵時間點集合
🧠 建模思路：

分析每條支路變化趨勢的結構性：

線性函數：2點可定

分段線性函數：每段2點，段間1點斷點
周期函數：至少1個周期的采樣點（3個關鍵點即可擬正弦函數）
燈控函數：需覆蓋紅綠交界（至少每周期2~3點）

分析：
問題2中應在每段起止點選關鍵時刻（如 7:48、8:14 等

問題3中需覆蓋所有燈控狀態變化點，如 7:06, 7:16, 7:24…

匯總這些點作為最少采樣點，填寫表5.1