一、數量積運算
例題1

解析
首先,為了化簡運算過程,我們把OA、OB、OC向量記作a、b、c向量。
其次,充分利用已知條件,進行消元,兩邊平方,可以消除一個向量。
a → \mathop{a}\limits ^{\rightarrow} a→ * a → \mathop{a}\limits ^{\rightarrow} a→ =| a → \mathop{a}\limits ^{\rightarrow} a→ |*| a → \mathop{a}\limits ^{\rightarrow} a→ |
最后,把待求式向已知條件轉化。
最終得出答案

例題2

解析
由題知道,D點為BC中點。
從而,PA向量可以用AD和PD向量表示。
AD向量可以由AB和AC向量表示
得出最終結論
答案選D
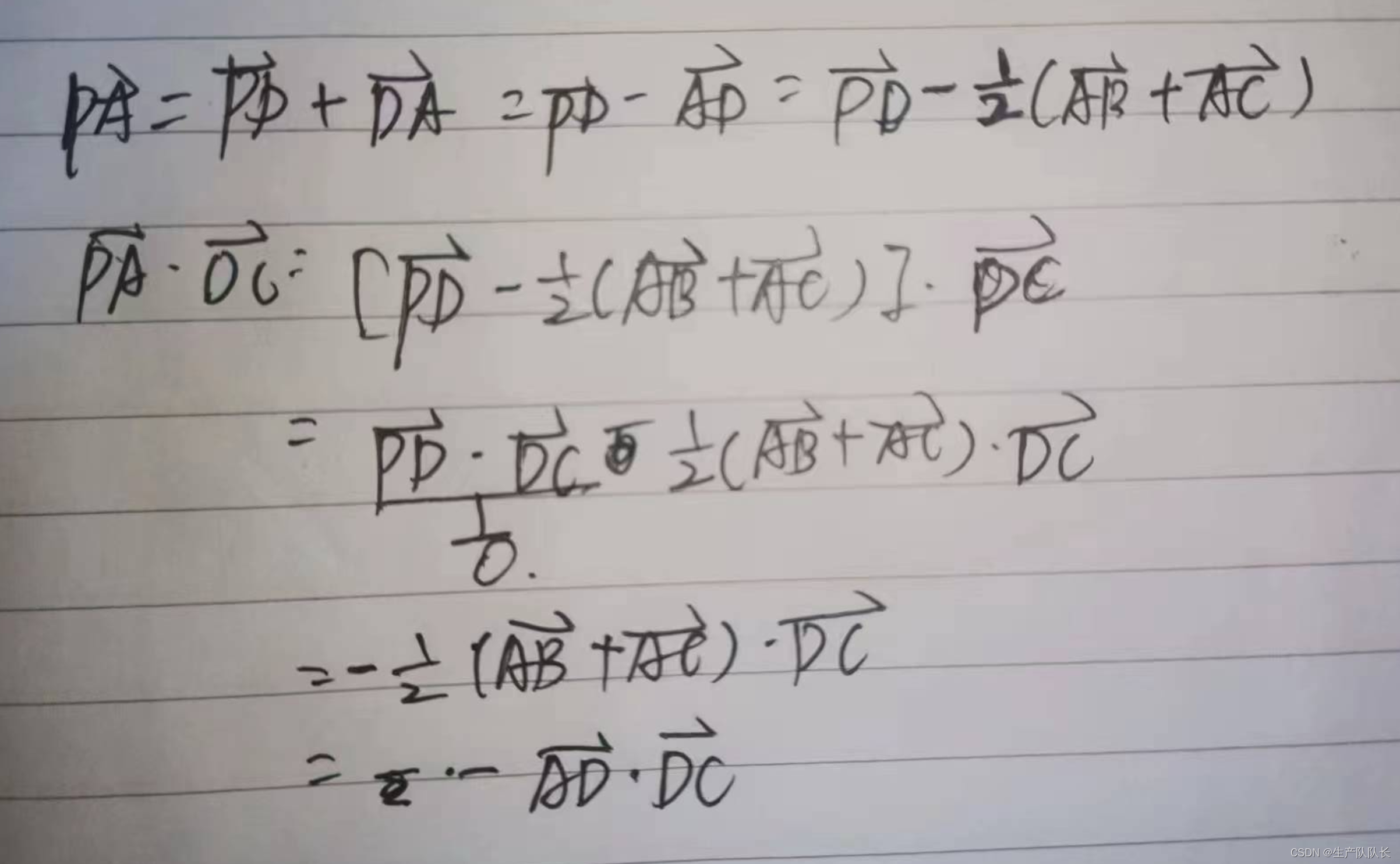
二、坐標運算
例題1

解析
這里有個默認規則,就是,四邊形ABCD的四個頂點是順時針或者逆時針的。不會出現交叉情況。
那么第一小問,就一種情況的四邊形。
很輕松就求出答案。
第二小問,難點在求最值這個地方。
a,b出現2次項,所以,我們可以用配方法,求最值。
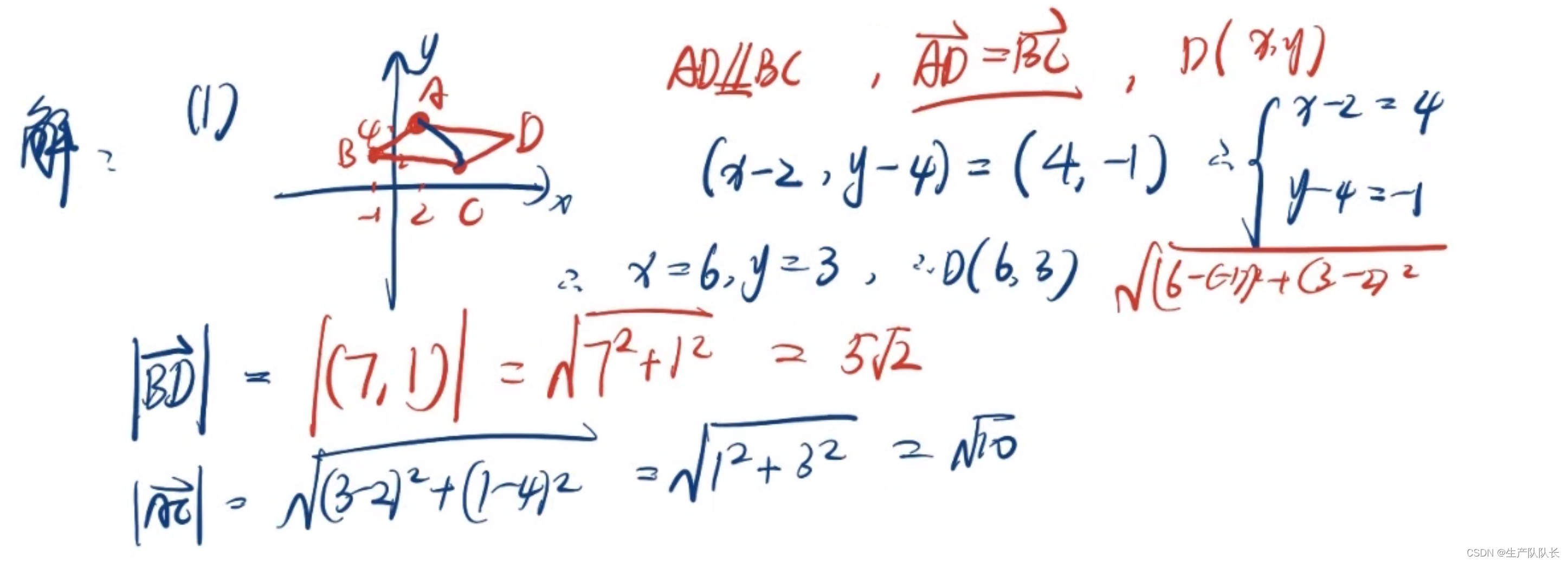

三、建坐標系法
通過該方法,把向量的數量積問題,轉化成向量的坐標運算問題
1、垂直向量可以建系
例題1
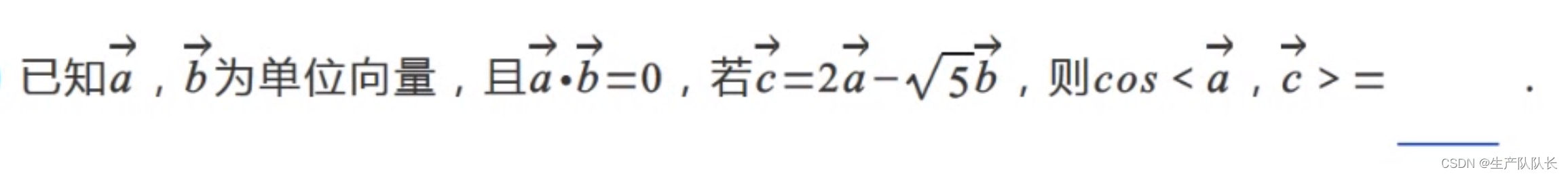
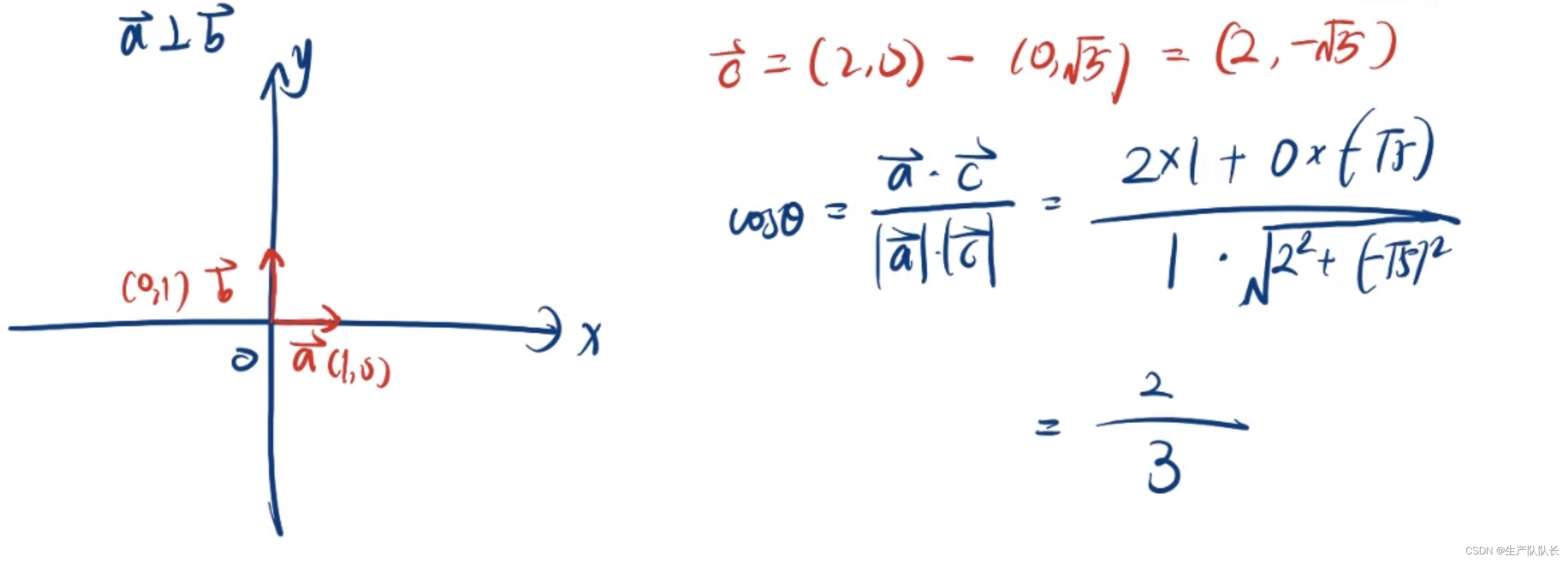
2、三角形中線可以建系
例題2
由于這一題沒有說明三角形是什么三角形,所以,我們可以找個特殊的等腰直角三角形來建系求解


3、等邊三角形可以建系
例題3


4、各種特殊圖像的建系方法
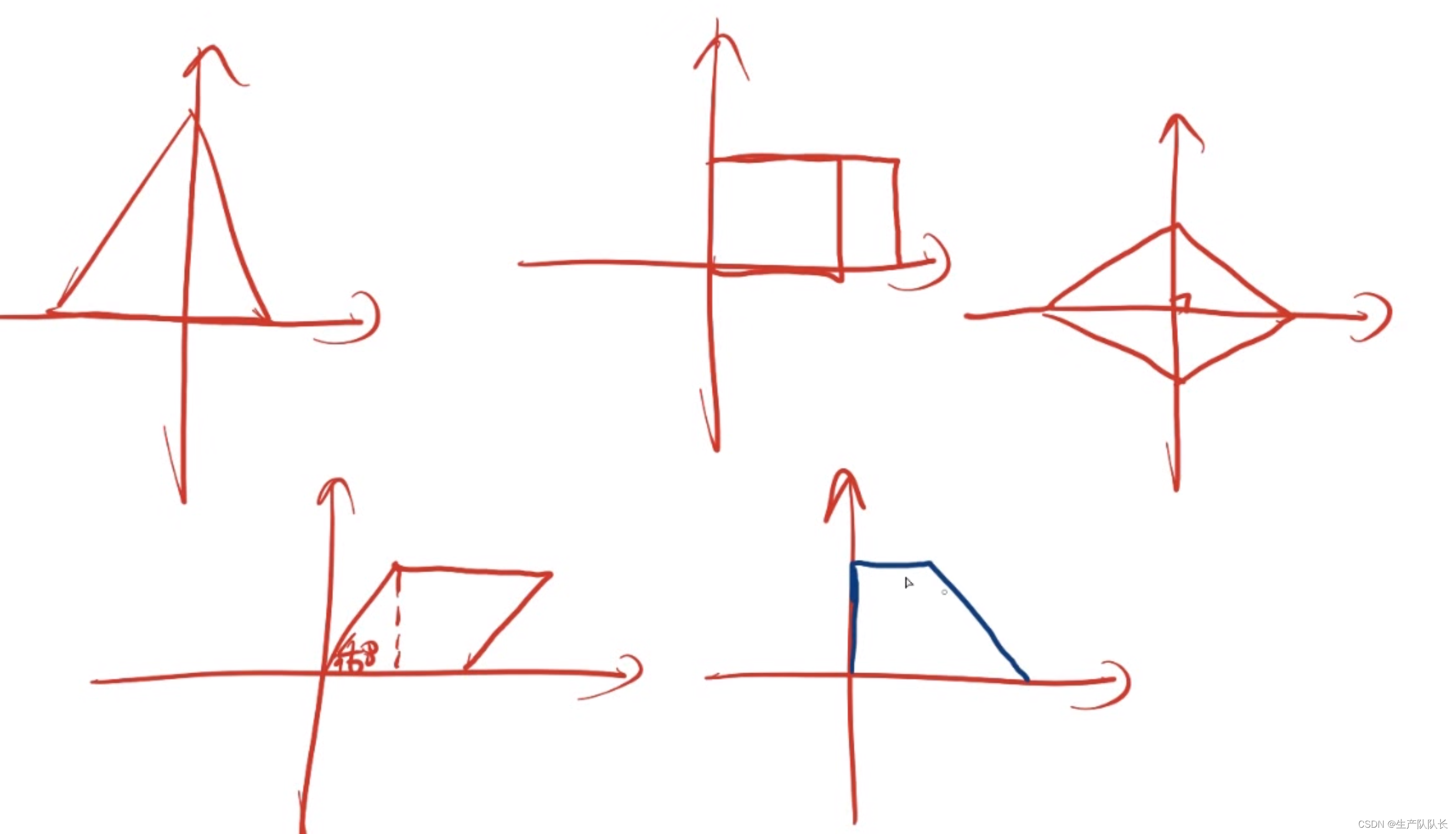
四、求兩向量和與差的模
例題1
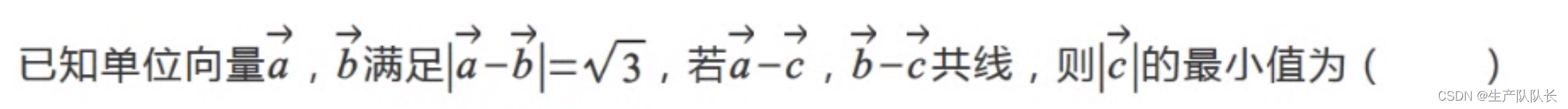
解析
此題有3種解法
都需要結合二元一次函數的最值求解
根據|a-b|=√3,可以求出向量a和向量b的夾角。
方法1,根據向量共線的定義,構建方程求解
方法2,根據這個夾角建立坐標系,在根據向量共線的坐標運算,構建方程求解
方法3,特殊三角形的幾何方法求解,適合做選擇題和填空題
方法1
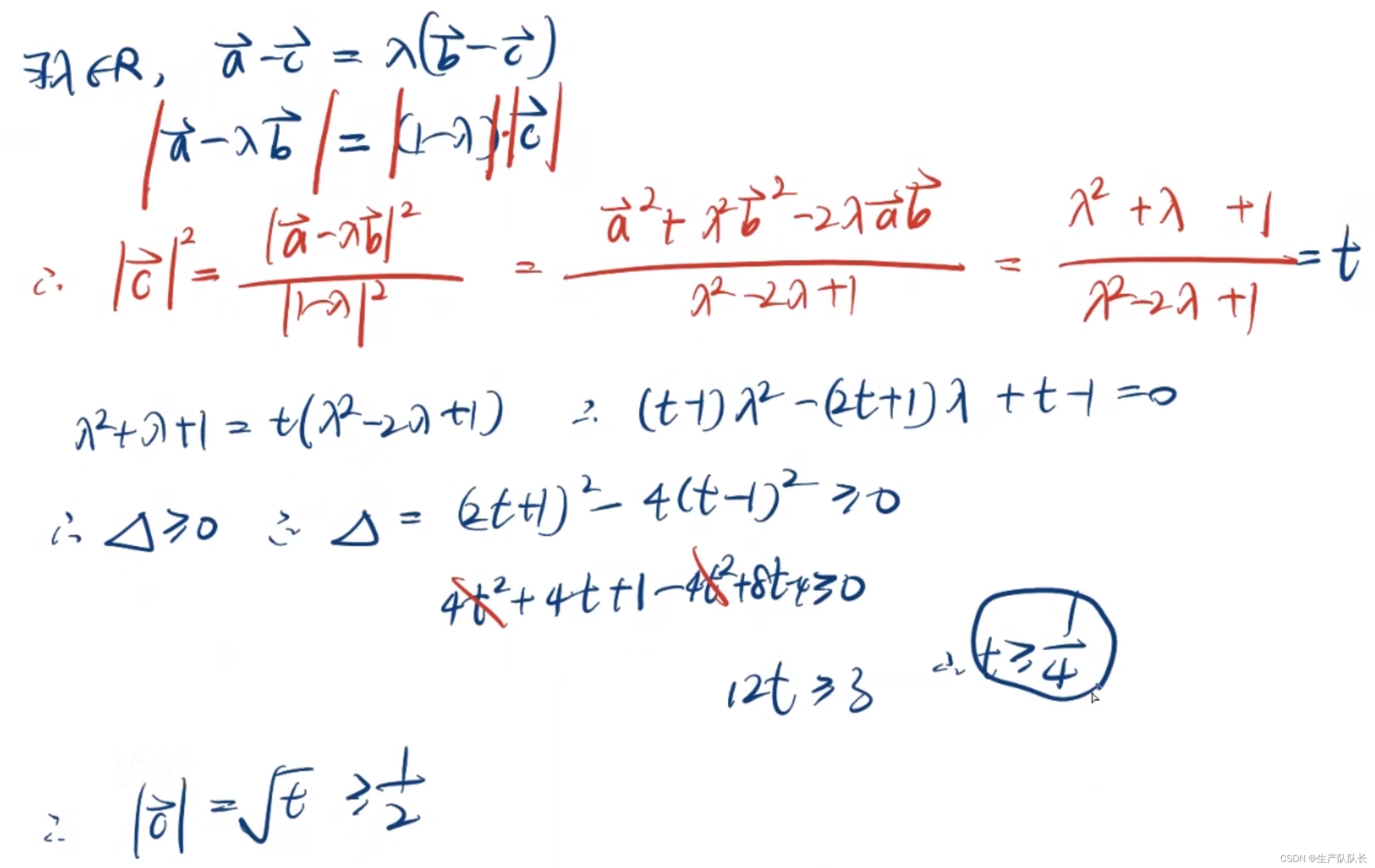
方法2

方法3


 Object Pascal 學習筆記---第14章泛型第2節(Object Pascal中的泛型))








)

)
)
(A~F2))




