1、背景介紹

? ? ? 實際中，很多人工構造物是由平面結構構造而成，如下圖所示，為一典型的由多個平面組成的人工構筑物。因此，根據離散點擬合成平面，獲取擬合平面方程，是點云數據處理中非常常見的數據處理操作。

2、平面擬合參數推導

? ? ? 基于若離散點，估算平面方程過程如下：

3、程序設計

? ? ? 基于上述理論，使用C++、PCL編寫的程序，下載鏈接如下：https://download.csdn.net/download/qq_32867925/89381863。

3.1 已知平面方程擬合測試

? ? ? 本次首先給定平面方程為x+2y+3z+4=0 （x+4y+5z+6=0）的平面，在平面上隨機生成50個點，利用這50個點擬合平面方程。部分結果與代碼如下：

int main()
{//a*x+b*y+c*z+d=0  平面方程形式double a, b, c, d;a = 1;b = 4;c = 5;d = 6;//隨機生成50個點// 初始化隨機數生成器srand(static_cast<unsigned int>(time(nullptr)));vector<pcl::PointXYZ> pts;for (int i = 0; i < 50; i++){pcl::PointXYZ pt;pt.x= static_cast<double>(rand()) / RAND_MAX;pt.y = static_cast<double>(rand()) / RAND_MAX;pt.z = (-d - a * pt.x - b * pt.y) / c;pts.push_back(pt);}NormalEigenvalueCurvature planeparam = EstimateNormalEigenvalue(pts);cout << "在平面方程為" << a << "x+" << b << "y+" << c << "z+" << d << "=0" << "平面上產生的點,經過擬合后得到的平面參數如下：" << endl;cout << "擬合參數 a b c d 分別如下：" << endl << "a=" << planeparam.normal_x << "  b=" << planeparam.normal_y << "  c=" << planeparam.normal_z << "  d=" << planeparam.d << endl;system("pause");return 0;
}

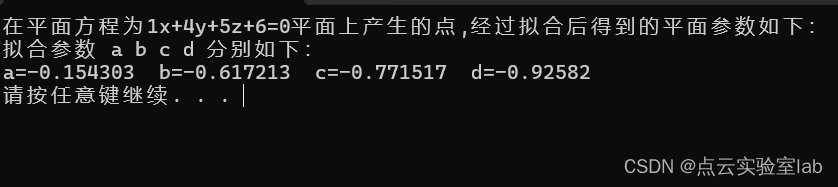
? ? ? 根據擬合可知，擬合得到的平面參數，與實現給定平面方程，幾乎一致，只是參數a、b、c進行了單位歸一化。證明了本方法的正確性。

3.2 法向量估算

? ? ? 根據推導過程可知，平面方程ax+by+cz+d=0中參數a、b、c為平面法向量。使用kdtree搜索點云近鄰點，利用近鄰點擬合得到局部平面，將局部平面的法向量進行可視化，可以進一步驗證估算法向量是否正確。部分代碼與結果如下：

將估算的參數a、b、c作為法向量，并進行可視化代碼示意：

vector<NormalEigenvalueCurvature> ptsNormal = PtsEstimateNormalEigenvalue(pts, 15);//估算每個點平面方程//增加點云法向量pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);normals->width = pts.size();normals->height = 1;normals->resize(normals->width * normals->height);for (int i = 0; i < ptsNormal.size(); i++){double normal_x = ptsNormal[i].normal_x;double normal_y = ptsNormal[i].normal_y;double normal_z = ptsNormal[i].normal_z;double length = sqrt(normal_x * normal_x + normal_y * normal_y + normal_z * normal_z);normal_x = normal_x / length;normal_y = normal_y / length;normal_z = normal_z / length;normals->points[i].normal_x = normal_x;normals->points[i].normal_y = normal_y;//將法向量調整都朝向if (normal_z >= 0){normals->points[i].normal_z = normal_z;}else{normals->points[i].normal_z = -normal_z;}}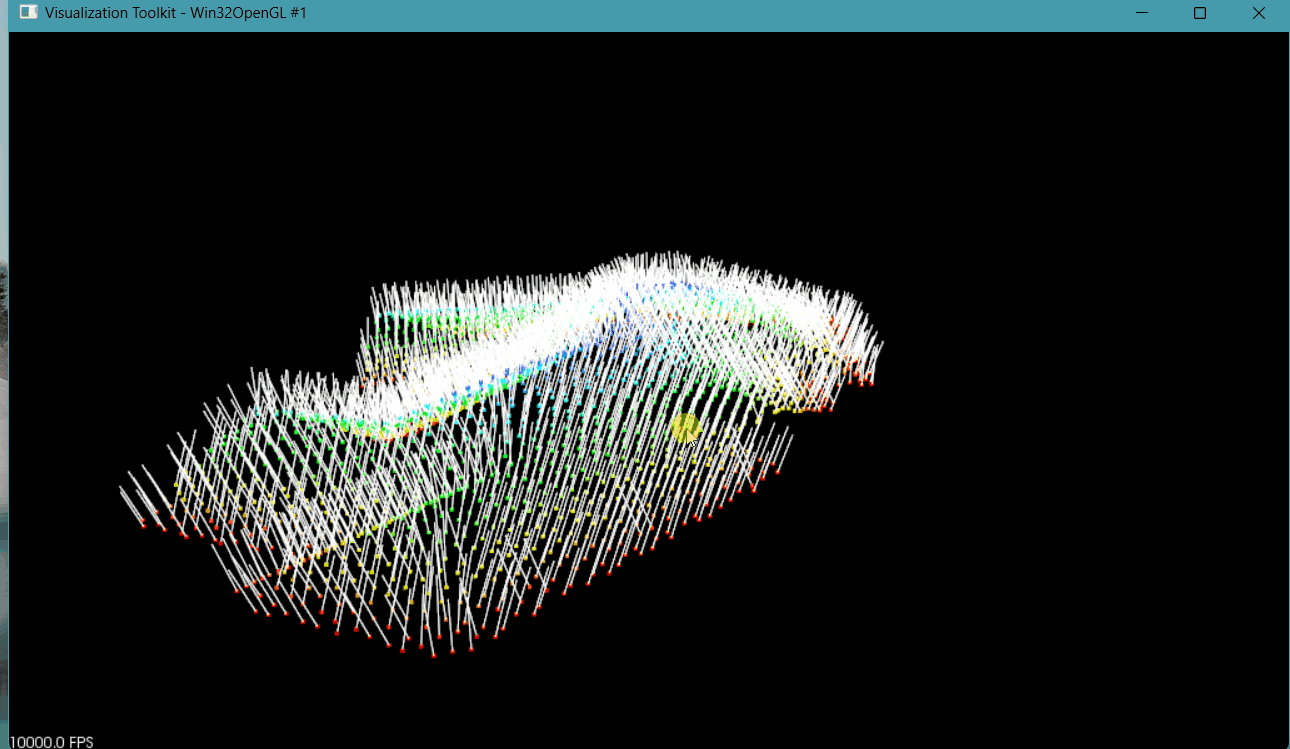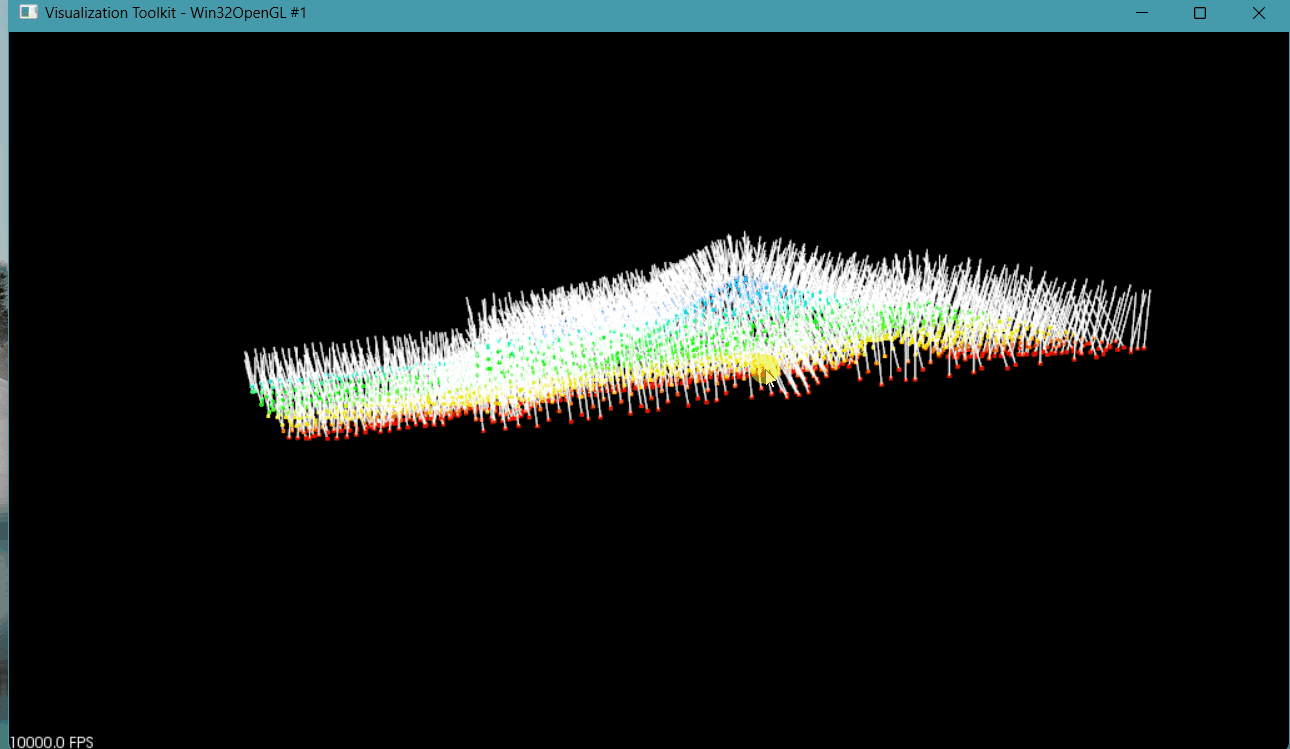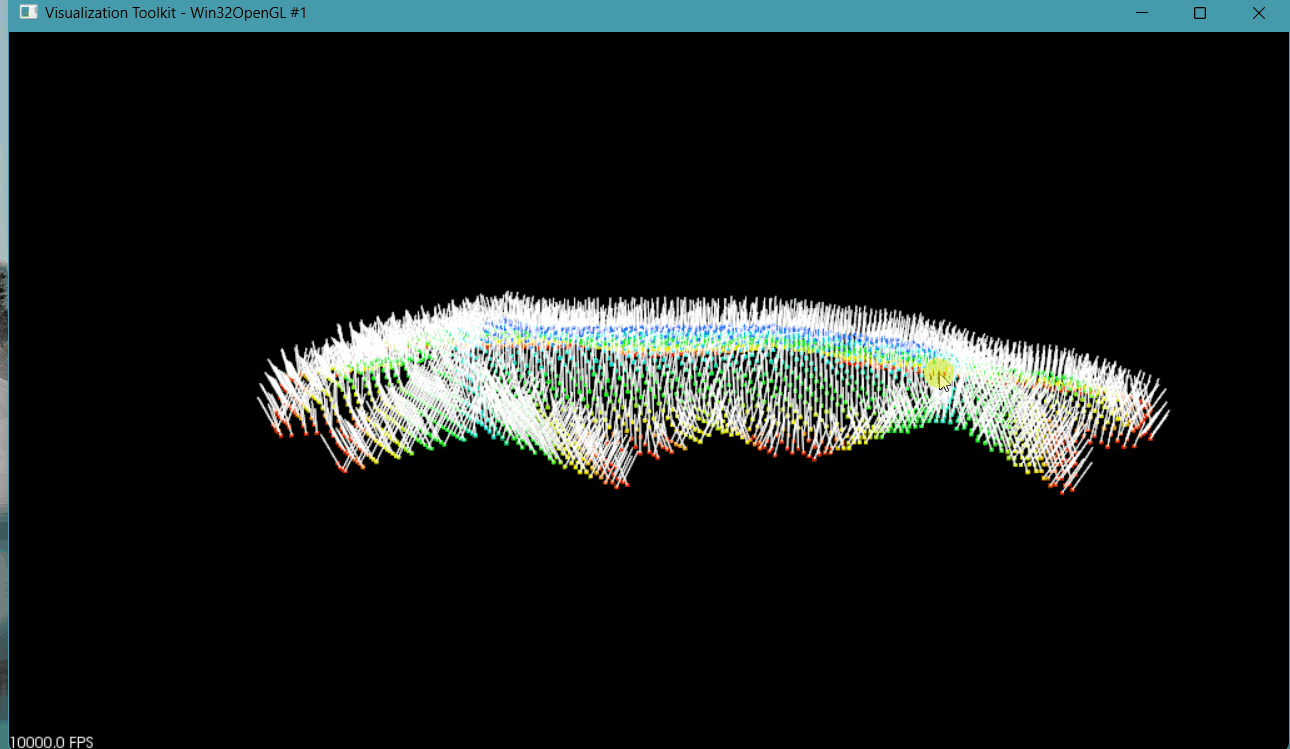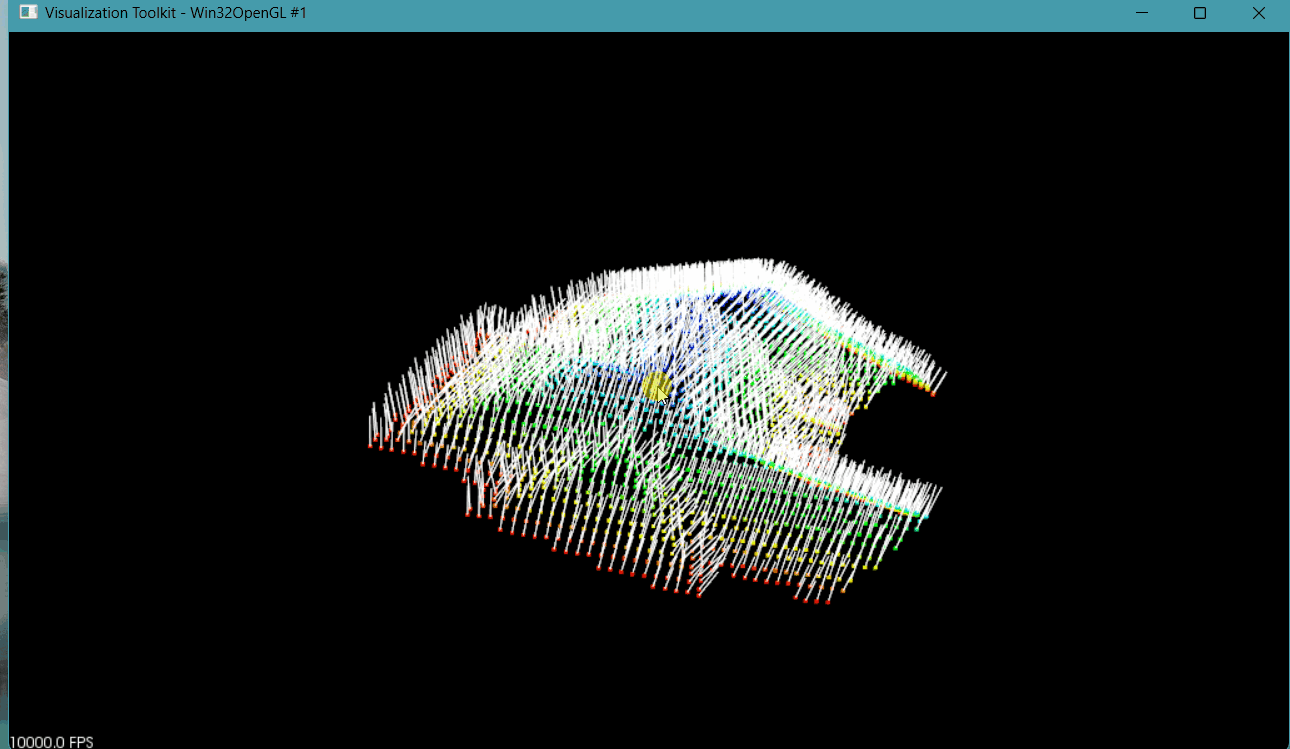

所有點法向量估算示意圖

? ? ? 由上圖可知，位于一個面上法向量是垂直于該平面的，證明估算法向量正確。

4、小結

? ? ?介紹了基于最小二乘估算平面方程的推導過程，以及測試結果。

基于PCL、C++編寫的代碼鏈接：https://download.csdn.net/download/qq_32867925/89381863