每日一題——Python實現PAT甲級1046 Shortest Distance（舉一反三+思想解讀+逐步優化）

一個認為一切根源都是“自己不夠強”的INTJ

個人主頁：用哲學編程-CSDN博客
專欄：每日一題——舉一反三
Python編程學習
Python內置函數

Python-3.12.0文檔解讀

我的寫法

專業點評

優點

改進建議

時間復雜度分析

空間復雜度分析

總結

我要更強

方法一：優化空間復雜度（保留前綴和）

方法二：直接使用距離數組進行查詢

代碼優化解釋

時間和空間復雜度分析

總結

哲學和編程思想

編程思想和哲學

總結

舉一反三

1. 空間換時間

2. 時間換空間

3. 貪心思想

4. 分治思想

5. 動態規劃

舉一反三的技巧

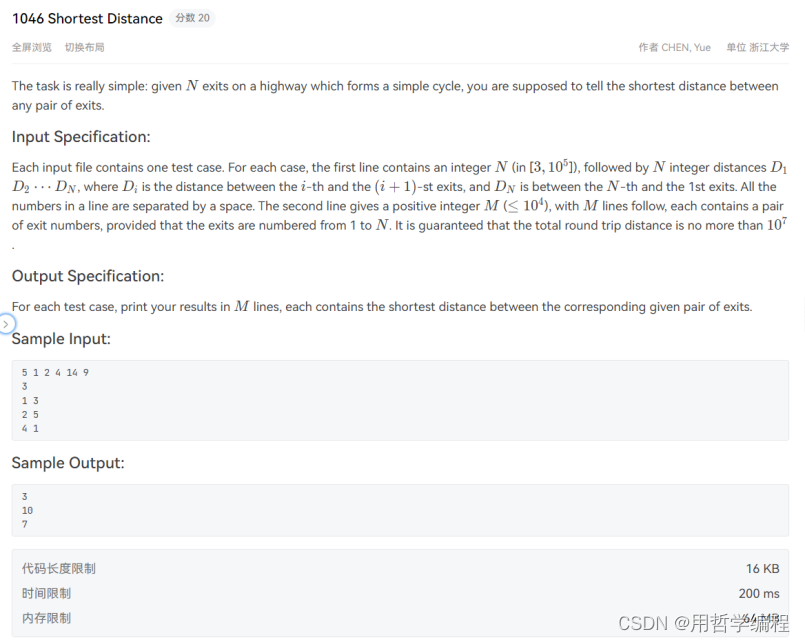
https://pintia.cn/problem-sets/994805342720868352/exam/problems/type/7?problemSetProblemId=994805435700199424&page=0

我的寫法

# 從輸入中讀取一行，將其拆分為整數，并存儲在 distances 列表中
distances = list(map(int, input().split()))# 第一個元素是 N，表示接下來行程的數目
N = distances[0]# 剩下的元素是各段行程的距離
distances = distances[1:]# 從輸入中讀取 M，表示要處理的查詢次數
M = int(input())# 創建一個前綴和數組，用于存儲從起點到各位置的累計距離
prefix_sum = [0] * (N + 1)# 計算前綴和數組
for i in range(1, N + 1):# prefix_sum[i] 表示從起點到第 i 段行程結束的累計距離prefix_sum[i] = prefix_sum[i - 1] + distances[i - 1]# 總的環形路徑的距離
total_distance = prefix_sum[N]# 處理每個查詢
for i in range(M):# 讀取查詢的兩個點 a 和 ba, b = map(int, input().split())# 確保 a 小于 b，如果不是則交換 a 和 bif a > b:a, b = b, a# 計算從 a 到 b 的路徑距離distance1 = prefix_sum[b - 1] - prefix_sum[a - 1]# 計算從 b 到 a（繞過環的另一邊）的路徑距離distance2 = total_distance - distance1# 輸出較短的路徑距離print(min(distance1, distance2))

這段代碼的功能是處理一個環形路徑的查詢問題，計算兩個節點之間的最短距離。以下是對這段代碼的點評，以及時間復雜度和空間復雜度的分析。

專業點評

優點

前綴和的使用：
- 通過前綴和數組?prefix_sum，可以在常數時間內計算任意兩點之間的路徑距離。這種方法有效地將路徑長度查詢的時間復雜度從線性降到常數。
處理環形路徑：
- 計算兩種可能的路徑（順時針和逆時針）并取最小值的方式，確保了找到兩點間的最短路徑。
輸入處理：

代碼通過?map?和?split?組合高效地讀取并轉換輸入，符合常見的Python代碼風格。

改進建議

輸入驗證：
- 沒有對輸入進行驗證假設輸入是正確的。可以增加對輸入數據的合法性檢查，確保輸入值在合理范圍內。
變量命名：

可以通過更具描述性的變量名（如?distance_clockwise?和?distance_counterclockwise）來提高代碼的可讀性。

時間復雜度分析

前綴和計算：
- 構建前綴和數組的時間復雜度為?O(N)，因為需要遍歷距離數組一次。
查詢處理：
- 每次查詢的時間復雜度為?O(1)，因為計算路徑距離和比較最小值的操作都是常數時間內完成的。
總體時間復雜度：

總體時間復雜度為?O(N+M)，其中?N?是距離數組的大小，M?是查詢次數。

空間復雜度分析

前綴和數組：
- 需要一個大小為?N+1?的前綴和數組?prefix_sum，空間復雜度為?O(N)。
輸入存儲：
- distances?數組存儲每段行程的距離，空間復雜度為?O(N)。
總體空間復雜度：

總的空間復雜度為?O(N)，因為額外使用的主要是?distances?和?prefix_sum?數組。

總結

這段代碼使用前綴和技巧有效地解決了環形路徑的最短距離查詢問題，時間復雜度為 O(N+M)，空間復雜度為O(N)。整體實現高效、簡潔，但可以通過增加輸入驗證和更清晰的變量命名進一步提高代碼質量。

我要更強

在這個問題中，由于我們需要進行多次查詢，而每次查詢都需要計算兩點之間的最短距離，前綴和的使用已經是一種非常高效的方案。進一步優化時間復雜度已經較為困難，因為查詢已經是 O(1) 的時間復雜度。

然而，我們可以考慮優化空間復雜度，特別是當 N 非常大時。以下是幾種可能的優化方法：

方法一：優化空間復雜度（保留前綴和）

盡管前綴和數組的空間復雜度是 O(N)，但它已經是當前任務的較優解。如果我們希望進一步減少空間消耗，可以考慮在查詢中實時計算部分前綴和，而不是存儲整個前綴和數組。然而，由于查詢次數 M 通常大于路徑段數 N，這種方法可能并不會帶來實際的性能提升。

方法二：直接使用距離數組進行查詢

如果我們不使用前綴和數組，而是直接從距離數組中計算路徑長度，雖然會增加每次查詢的時間復雜度，但可以節省空間。

下面是直接使用距離數組進行查詢的代碼示例：

# 讀取輸入
distances = list(map(int, input().split()))
N = distances[0]
distances = distances[1:]
M = int(input())# 計算總距離
total_distance = sum(distances)# 處理每個查詢
for _ in range(M):a, b = map(int, input().split())if a > b:a, b = b, a# 計算從 a 到 b 的路徑距離distance1 = sum(distances[a-1:b-1])# 計算從 b 到 a（繞過環的另一邊）的路徑距離distance2 = total_distance - distance1# 輸出較短的路徑距離print(min(distance1, distance2))

代碼優化解釋

輸入讀取和初始化：
- 讀取并解析輸入，distances?包含各段行程的距離。
總距離計算：
- 計算環形路徑的總距離。
查詢處理：

對每個查詢，計算從?a?到?b?的兩種路徑距離，輸出較小的值。