本篇會加入個人的所謂魚式瘋言

??????魚式瘋言:??????此瘋言非彼瘋言

而是理解過并總結出來通俗易懂的大白話,

小編會盡可能的在每個概念后插入魚式瘋言,幫助大家理解的.

🤭🤭🤭可能說的不是那么嚴謹.但小編初心是能讓更多人能接受我們這個概念 ！！！

前言

在上篇中我們學習了 二叉樹的基本概念 以及他們的特性結論，并運用到了 具體的題目 中去解決問題 。

而在本篇中，小編講繼續學習 二叉樹 的基本操作, 主要圍繞著我們 遍歷二叉樹 來講解 ， 人狠話不多，下面讓我們切入主題吧 💥 💥 💥

目錄

1. 二叉樹的遍歷初識

2. 前序遍歷

3. 中序遍歷

4.后序遍歷

5. 層序遍歷

6. 二叉樹遍歷的應用

一. 二叉樹的遍歷初識

學習二叉樹的結構，最簡單的方式就是遍歷，所謂遍歷 是指 沿著某條搜索路線，依次樹中的某個節點均做一次訪問， 訪問節點所做的操作 依賴于要解決的各種實際問題。

遍歷是二叉樹是最重要的操作之一，是 二叉樹上進行其他運算 的基礎

1. 二叉樹的遍歷簡介

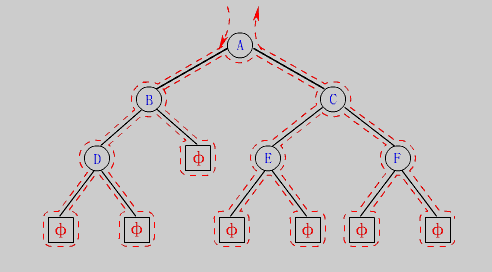
在遍歷二叉樹時， 如果沒有進行某種約定，每個人都按照自己的方式來遍歷， 得到的結果就比較亂， 如果我們按照某個規則 來遍歷， 則每個人對于遍歷結果都是相同的 ， 如果 N 代表 根節點，L 代表左節點， R 代表 右節點， 那根據遍歷的的節點有以下的遍歷方式。

• NLR： 前序遍歷 (先序遍歷) 根據 根——》 左 ——》 右 的順序對二叉樹進行遍歷

• LNR : ==中序遍歷 ==： 根據 左——》 根——》 右 的順序 對二叉樹進行遍歷

• LRN 后序遍歷 : 根據 左——》 右 ——》 根 的順序對二叉樹進行遍歷

詳細的遍歷方式， 小編下面細講哦 💖 💖 💖 💖

在遍歷二叉樹之前， 我們先用一下代碼簡單的 構建一顆二叉樹

public class MyBinaryTree {public static class TreeNode {public TreeNode left;public TreeNode right;public  char val;public TreeNode(char val) {this.val = val;}}private TreeNode  root;// 構造二叉樹public TreeNode createBinaryTree() {root=new TreeNode('A');TreeNode B=new TreeNode('B');TreeNode D=new TreeNode('D');TreeNode E=new TreeNode('E');TreeNode H=new TreeNode('H');TreeNode C=new TreeNode('C');TreeNode F=new TreeNode('F');TreeNode G=new TreeNode('G');root.left=B;B.left=D;B.right=E;E.right=H;root.right=C;C.left=F;C.right=G;return root;}// 前序遍歷
void preOrder(Node root);
// 中序遍歷
void inOrder(Node root);
// 后序遍歷
void postOrder(Node root);}

二. 前序遍歷

1. 前序遍歷的特點

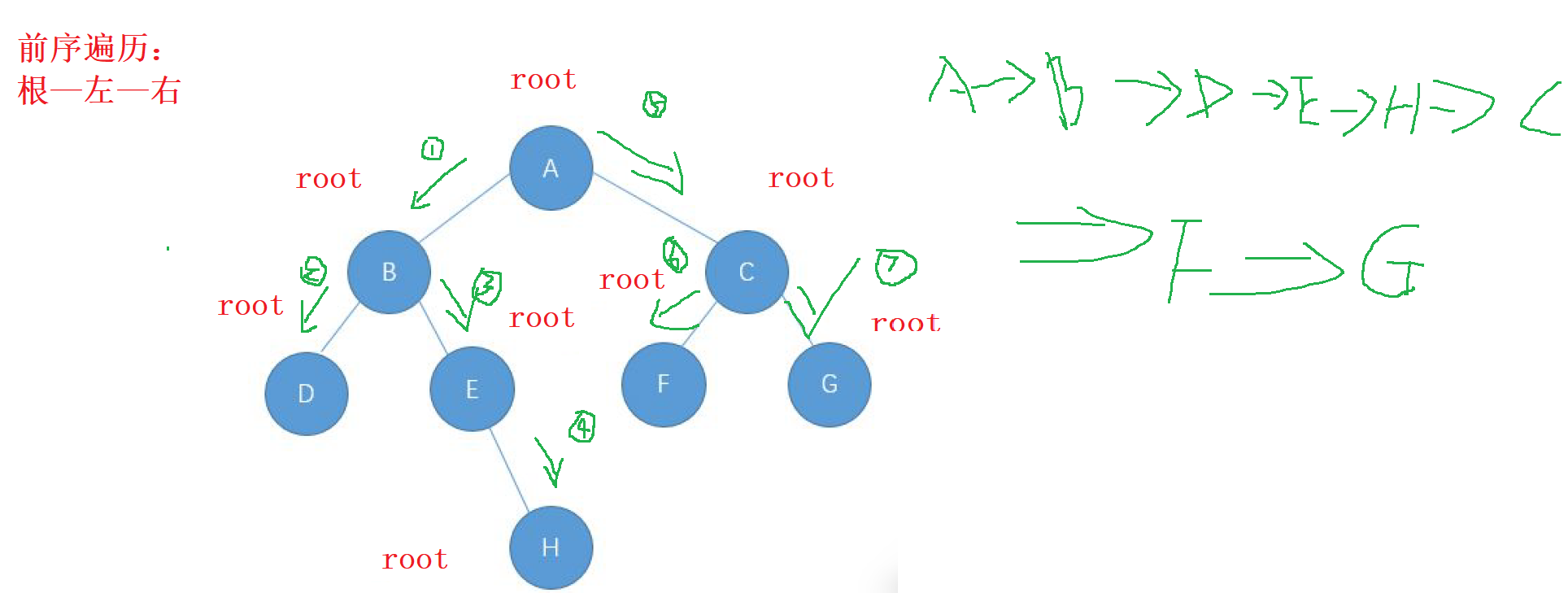
按照從左子樹開始走，一直 往下遞歸，每一步所走的路徑成為我們的根，先遍歷完根之后。

按照根左右的順序， 當我們走完每個根節點的左子樹 時， 先往下遞， 再往回歸 , 左節點成為新的根， 會到最初的根節點之后，再向右子樹進行 先遞后歸 的操作,

動畫演示

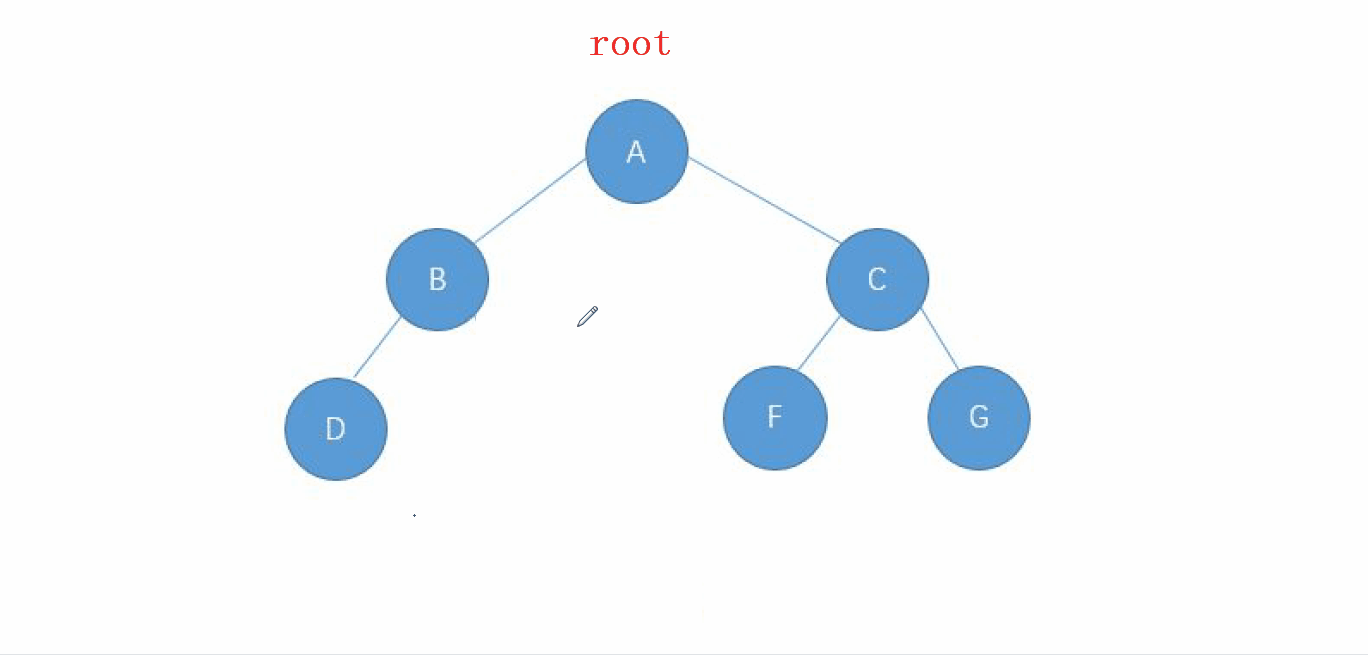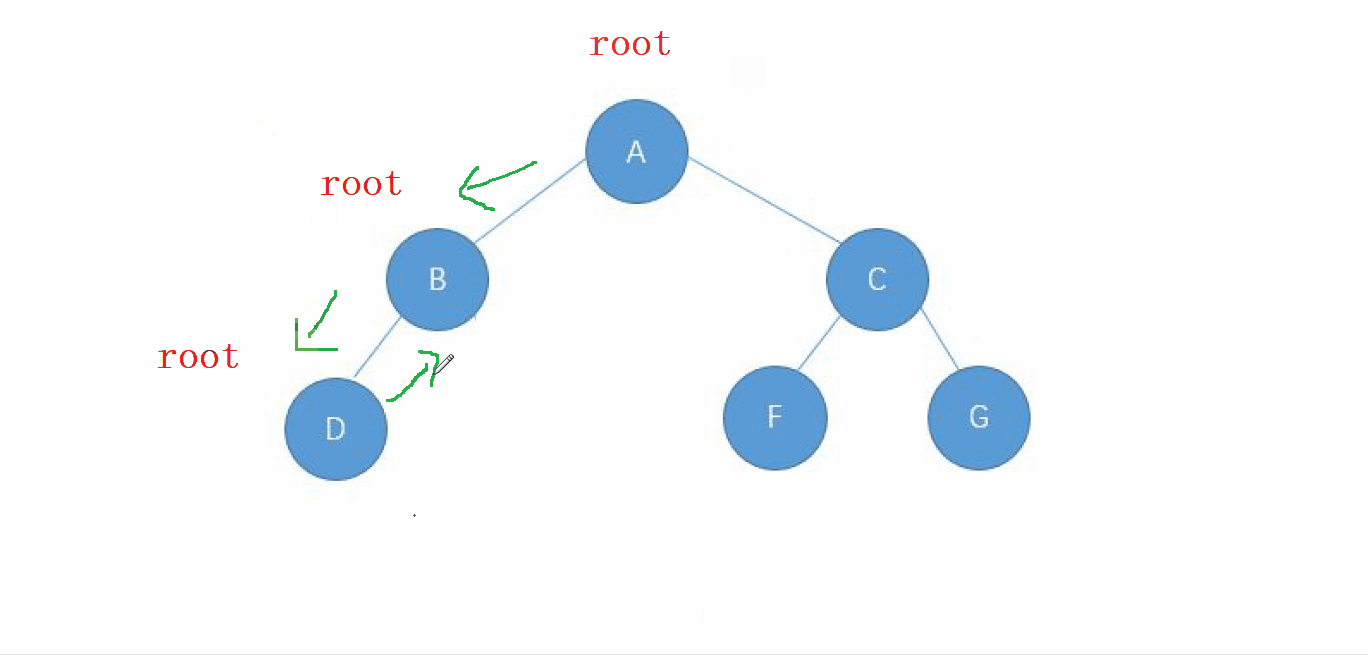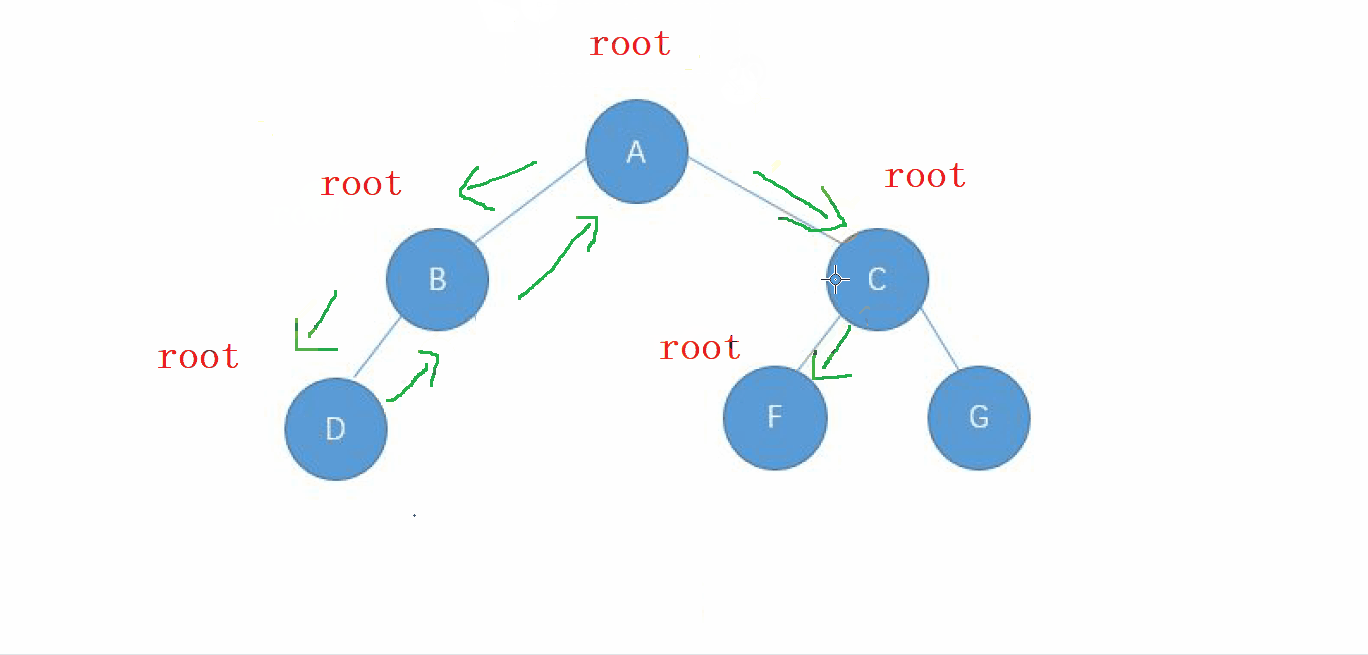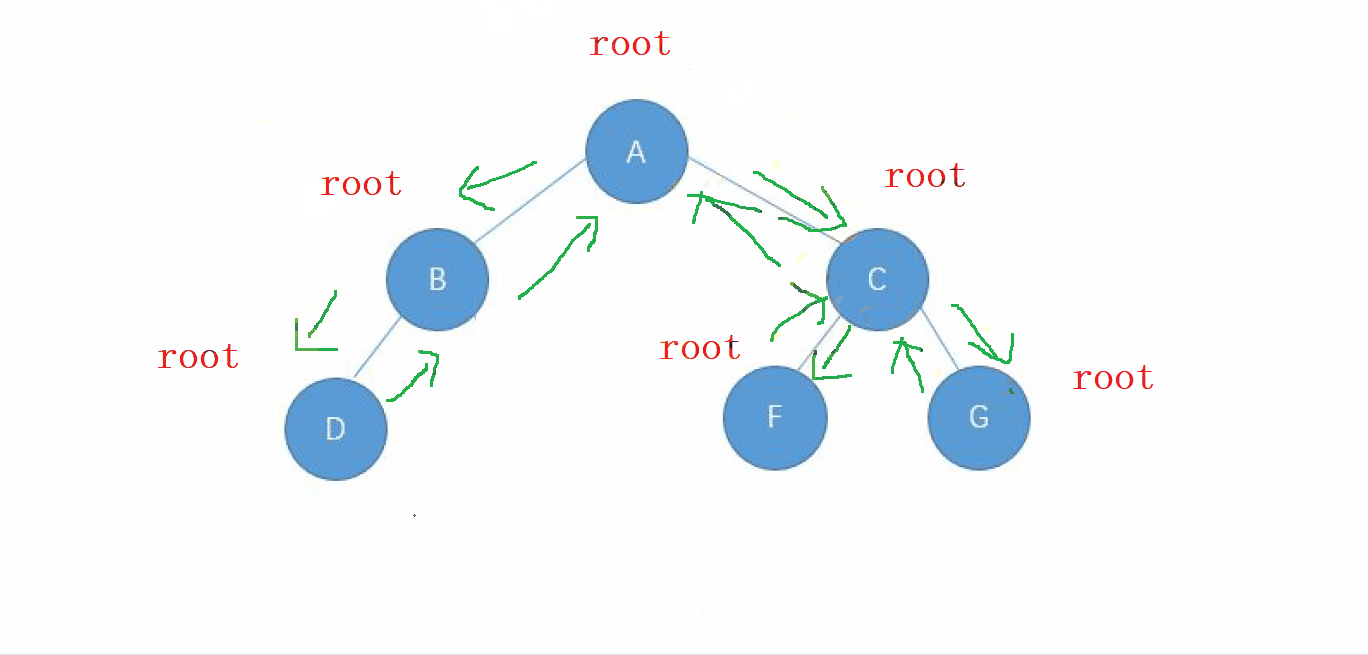
2. 前序遍歷的實現

因為前序遍歷有 遞歸 和 非遞歸 的兩種方式， 但 遍歷的原理和方向都是一致的

在本篇文章中，。小編都會帶著小伙伴們 一 一 實現 💥 💥 💥 💥

<1>. 前序遍歷的遞歸實現

   // 前序遍歷public void FirstDisplay(TreeNode root) {if (root==null) {return;}System.out.print(root.val+" ");FirstDisplay(root.left);FirstDisplay(root.right);}

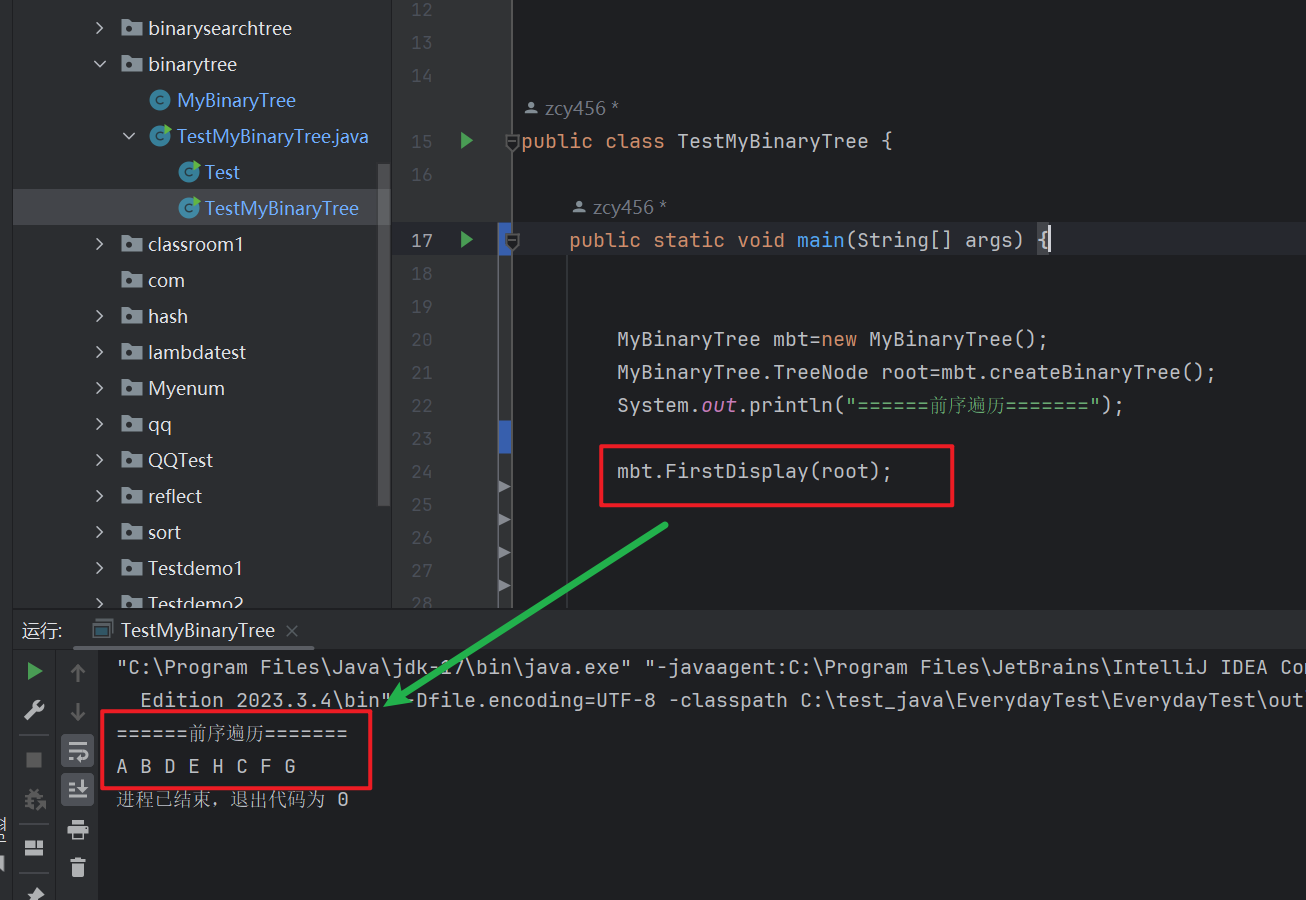
這里的代碼的遞歸思路就是完美的按照我們遍歷方向來的， 先訪問，后遞歸

<2>. 前序遍歷的非遞歸實現

// 非遞歸的前序遍歷public  void  FirstDisplayNo(TreeNode root) {// 先創建一個棧來存放樹的每個節點Stack<TreeNode> stack=new Stack<>();// 先把艮節點創建一遍TreeNode cur=root;/*** 外循環主要遍歷 右邊的節點* 用于出棧的數據* 并讓節點向右移動*/while (cur != null || !stack.empty()) {/*** 在這個內循環中* 當往左走就添加數據，一直到為 null 結束*  并進行打印*/while (cur != null) {// 先打印System.out.print(cur.val+" ");// 打印完就入棧stack.add(cur);// 節點向左移動cur=cur.left;}// 出棧存放數據cur=stack.pop();// 并向右走cur=cur.right;// 當再次循環時，如果左邊還有節點就會繼續存放}System.out.println();}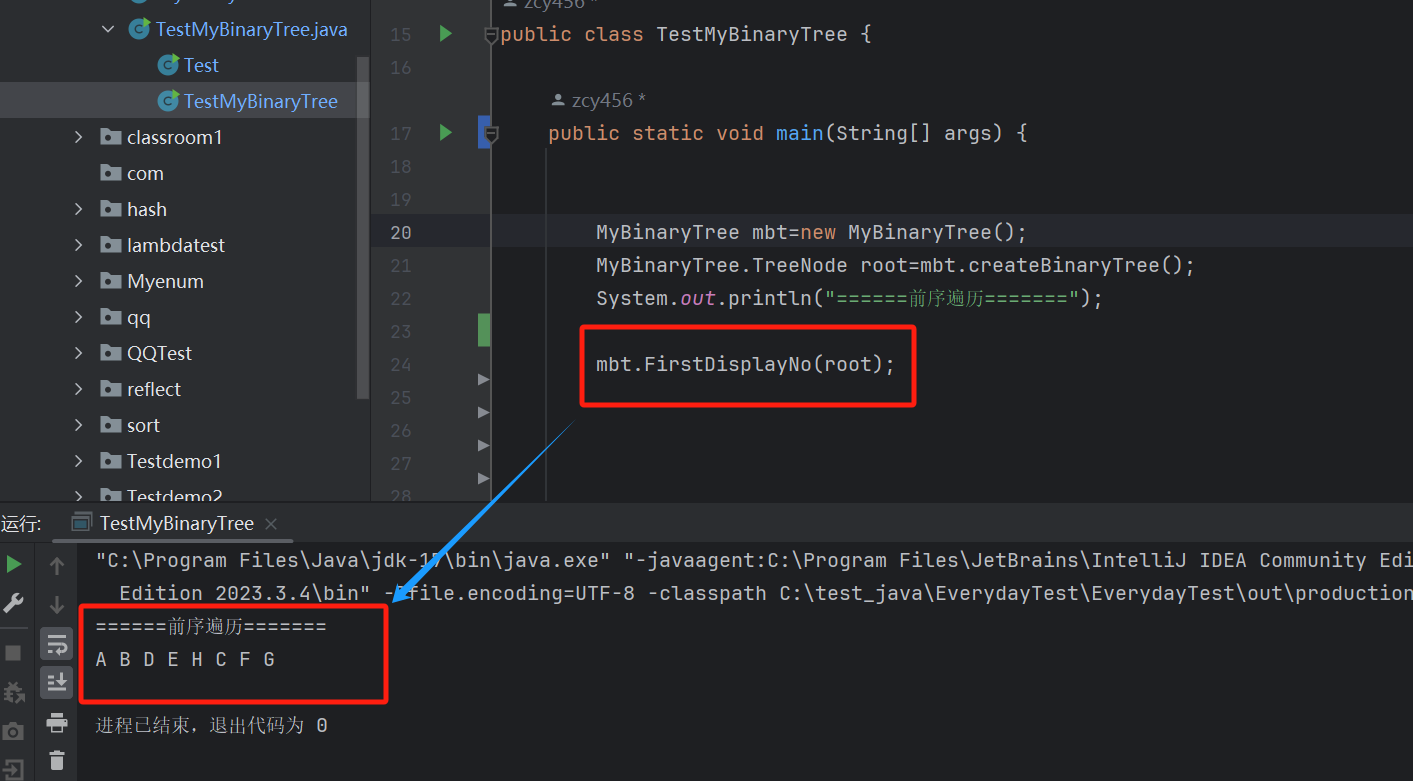

非遞歸的 實現步驟

1. 先定義一個棧 ， 來記錄我們每次遍歷過的 根節點

2. 先讓根節點一直 向左走 ，當遍歷完我們的 左子樹 （也就是我們的 root = null 時候）， 并且入棧， 記錄下來以便后面我們遍歷 右子樹

3. 然后出棧， 開始 向右走 ， 遍歷我們的 右子樹

4. 當整個棧為 null 并且到達的這個節點 cur 也為 null ， 就意味著遍歷完整個 二叉樹所有的節點

魚式瘋言

無論是 遞歸還是非遞歸的 前序遍歷 , 我們的 前序遍歷思路就是

先走根 ， 根走完走左 ， 左走完回到根， 再走右 ，一層一層的走， 一步一步的回 。

細節處理：

在代碼上我們要注意的就是這個當節點為 null ，也就意味著我們要開始 回退 到 上一個節點

二. 中序遍歷

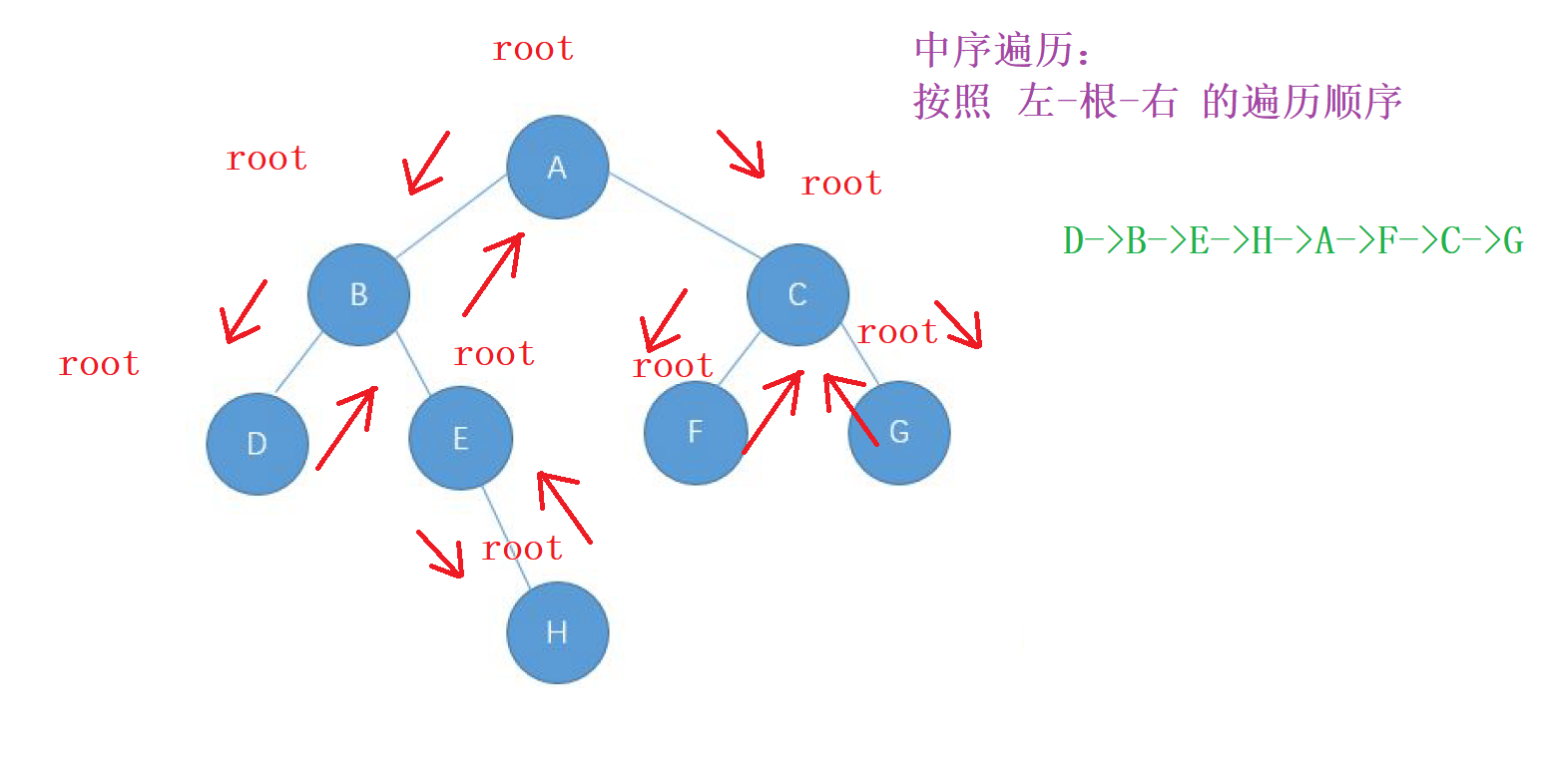
1. 中序遍歷的特點

我們知道 中序遍歷 ， 是以 左- 根-右的順序 進行遍歷

我們先從 走左邊， 還是讓每個左節點先成為新的根， 當這個新的根的 左子樹 都走完之后， 才能真正訪問我們當前 新的節點。

以此類推，我們新的節點訪問結束后，就會進行回退到前一個舊的節點，繼續訪問，最終當整個 左子樹走完 ， 并且 訪問完我們的根 ， 就遍歷我們的右子樹 ，最終回到我們整顆樹的 根節點

動畫演示

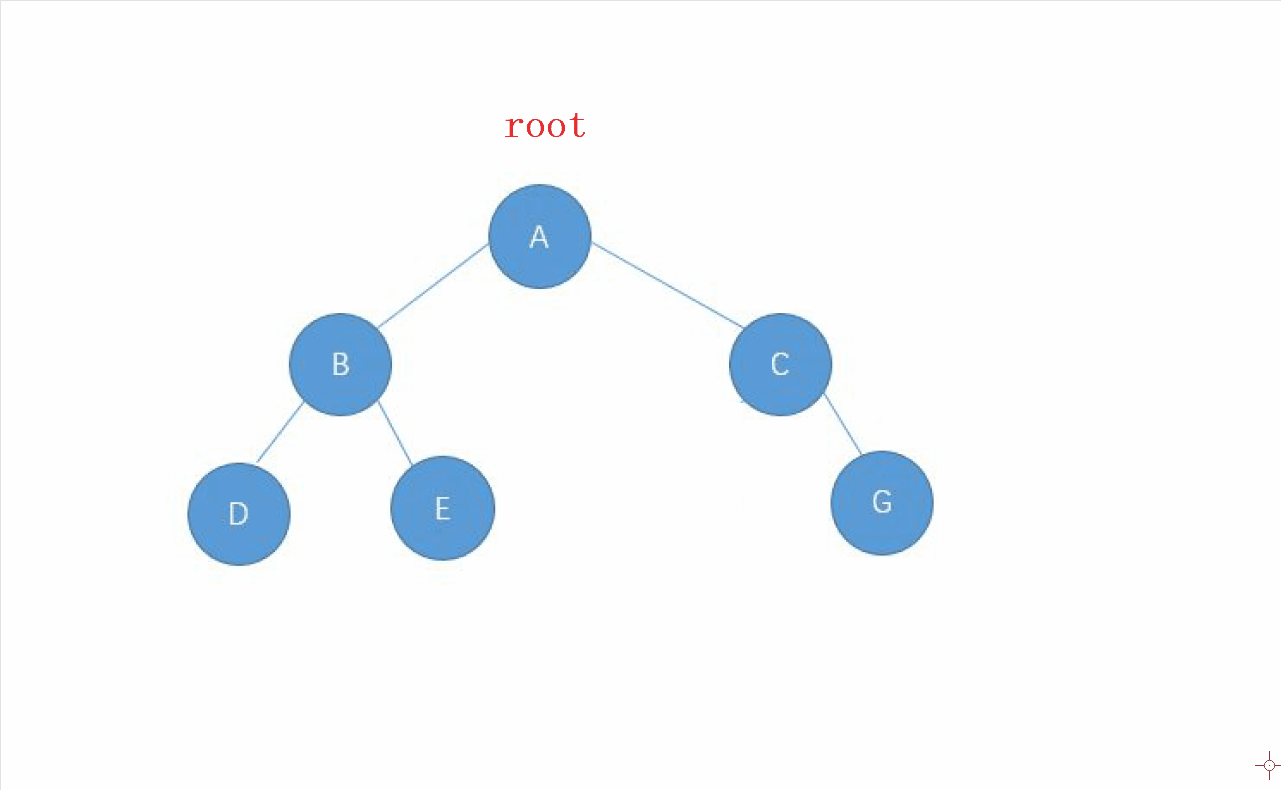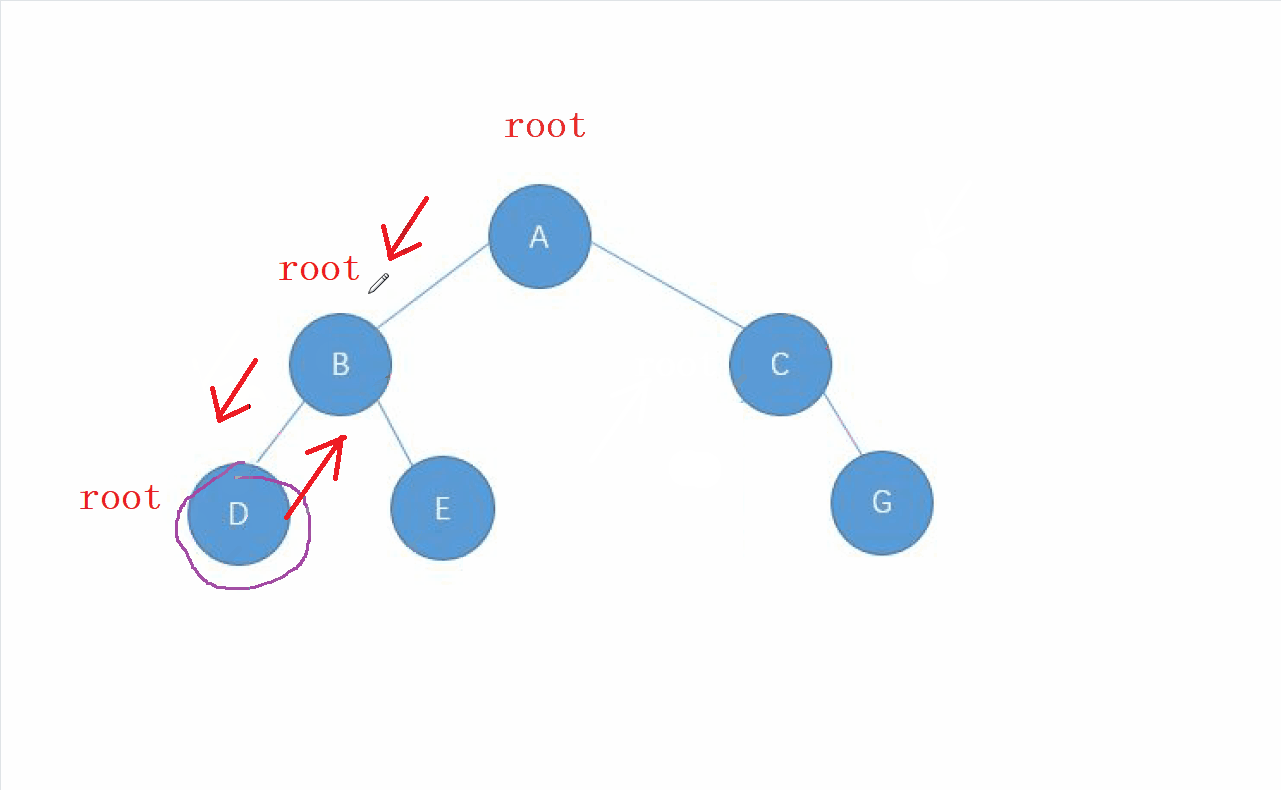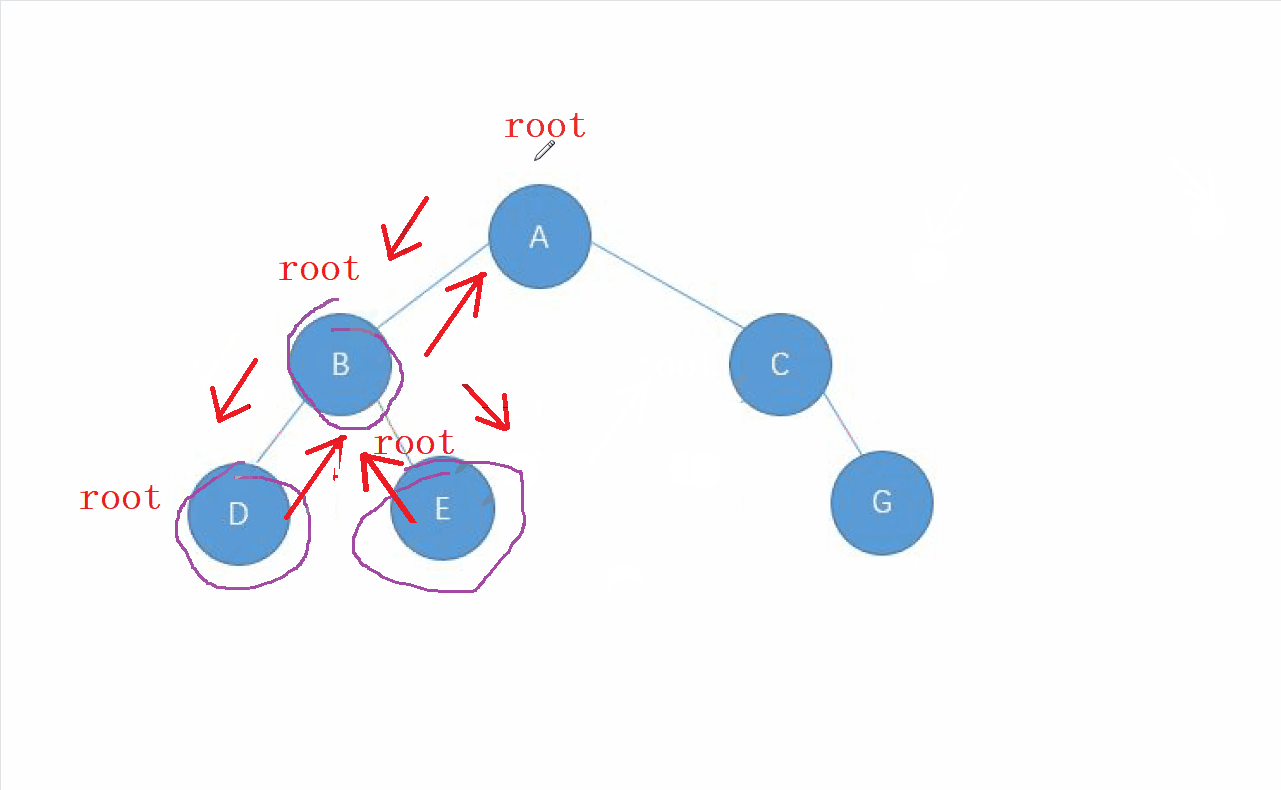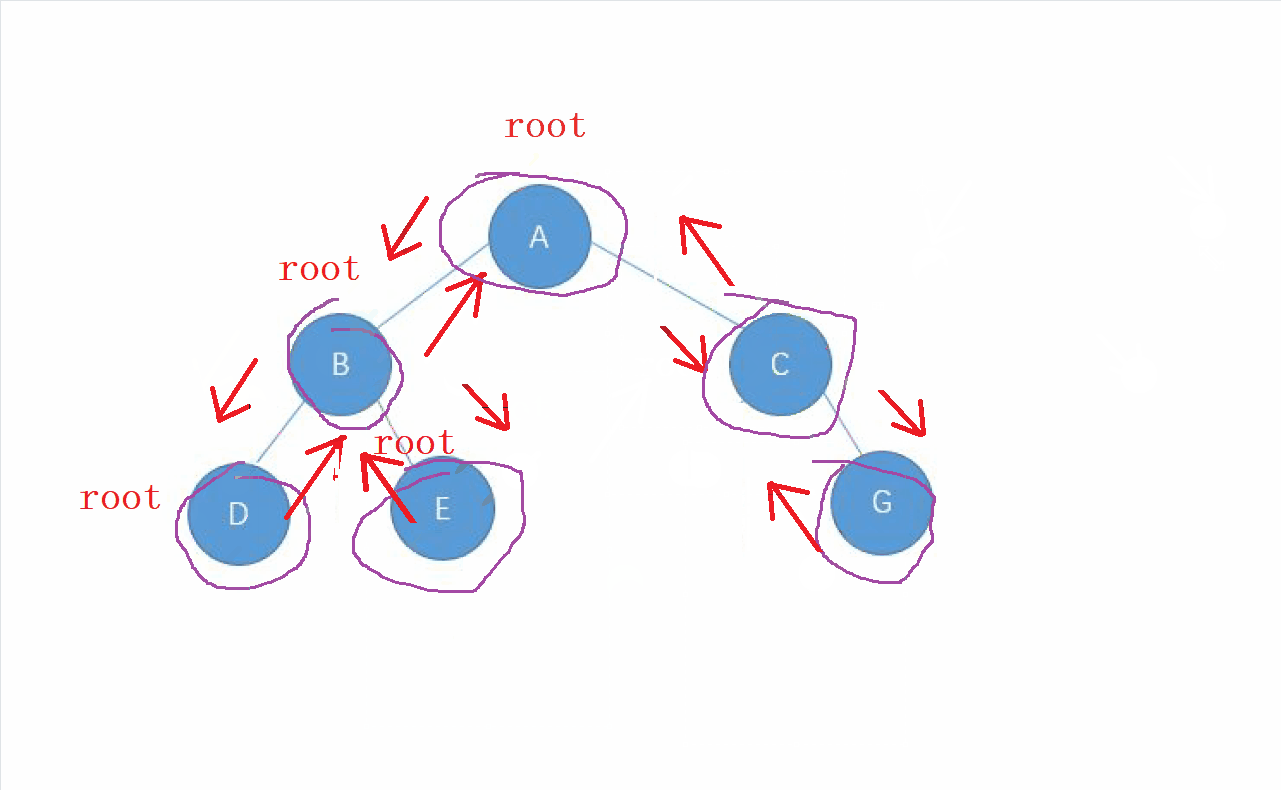
2.中序遍歷的實現

<1>.中序遍歷的遞歸實現

// 中序遍歷
public void middleDisplay(TreeNode root) {if (root==null) {return;}middleDisplay(root.left);System.out.print(root.val+" ");middleDisplay(root.right);
}

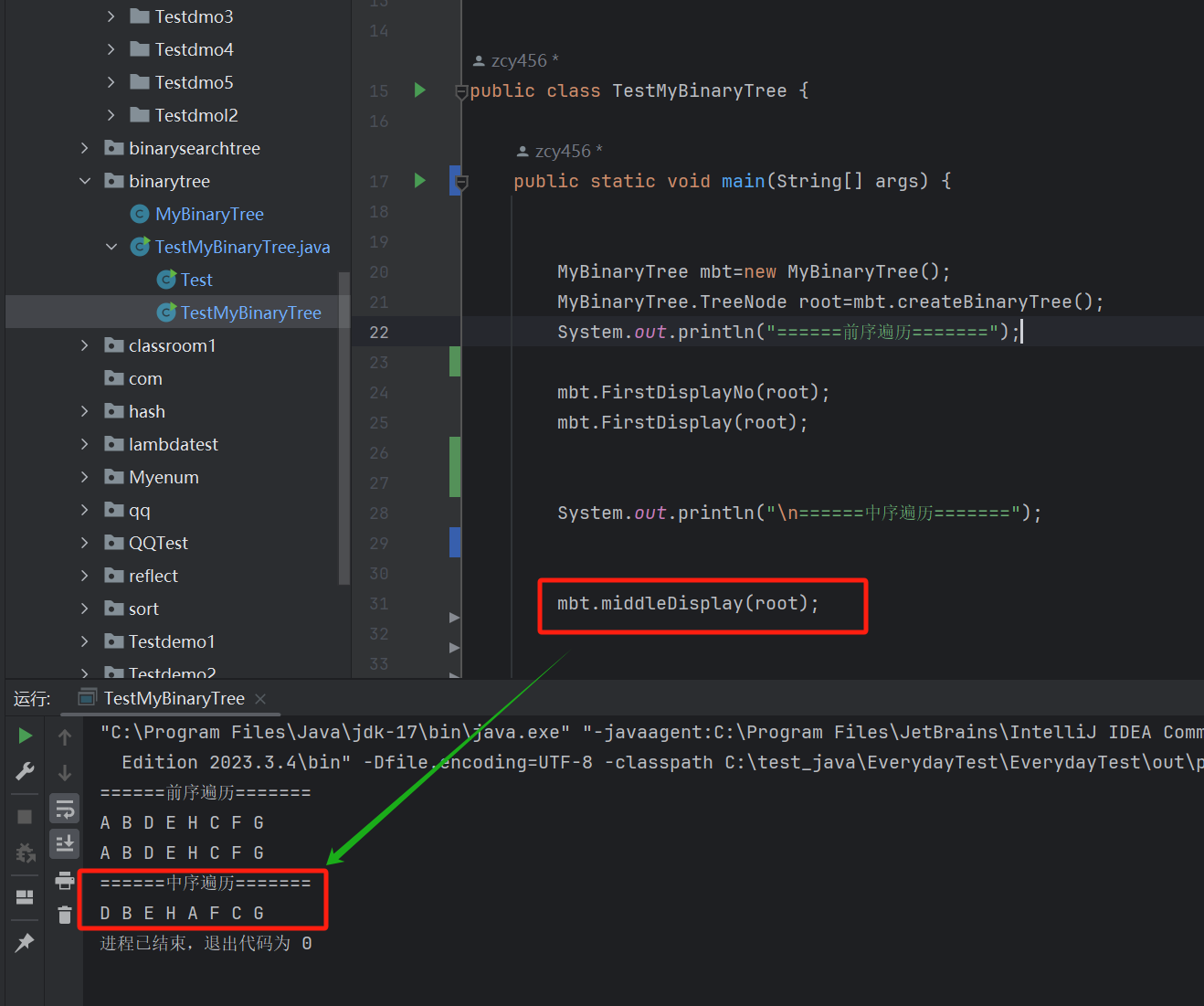
這里的代碼的遞歸思路就是完美的按照我們遍歷方向來的， 先遞歸，后訪問 ，小編在這里就 不贅述 了

<2>. 中序遍歷的非遞歸實現

// 非遞歸的中序遍歷public  void  middleDisplayNo (TreeNode root) {// 創建一個棧用于回退節點Stack<TreeNode> stack=new Stack<>();// 先放根節點TreeNode cur=root;/*** 外循環主要用于遍歷 右邊* 更是用于出棧的回退*/while (cur != null || !stack.empty()) {/*** 內循環先遍歷下去* 邊遍歷邊存放*/while (cur != null) {stack.add(cur);cur=cur.left;}// 出棧最后一個無左節點的左子樹cur=stack.pop();// 打印該節點System.out.print(cur.val+" ");// 再往右走cur=cur.right;}System.out.println();}

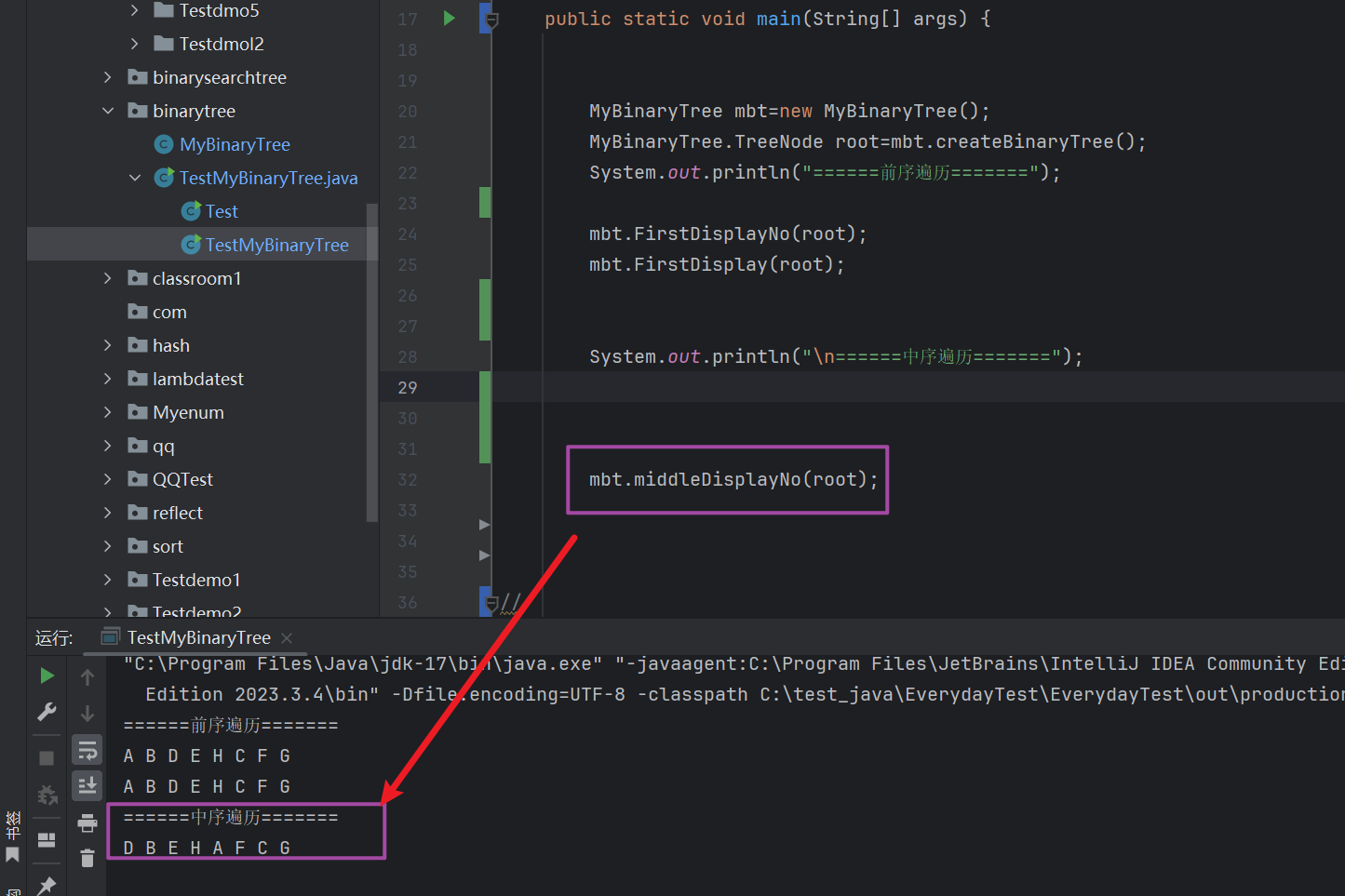
非遞歸的實現步驟：

我們先定義一個 棧 ，用來存儲走過的每個 左子樹的節點

1. 先 往左邊 的節點走，先整個左子樹 的每個節點都入棧， 當 這個節點 為 null 就 停止入棧

2. 然后進行出棧， 出棧的時候，我們就可以對該節點進行打印（訪問） ， 并且向 右子樹節點 開始走

3. 當整個棧為 null 并且 該節點也為 null ， 也就意味著遍歷完二叉樹 所有的節點

魚式瘋言

中序遍歷的最核心的要點就是

無論是 遞歸 還是 非遞歸 的 中序遍歷：

一定要先走完每個左子樹， 當我們進行 回退 的時候。 才輪的到該 根節點去遍歷， 最后才走 右子樹的一種 順序.

三. 后序遍歷

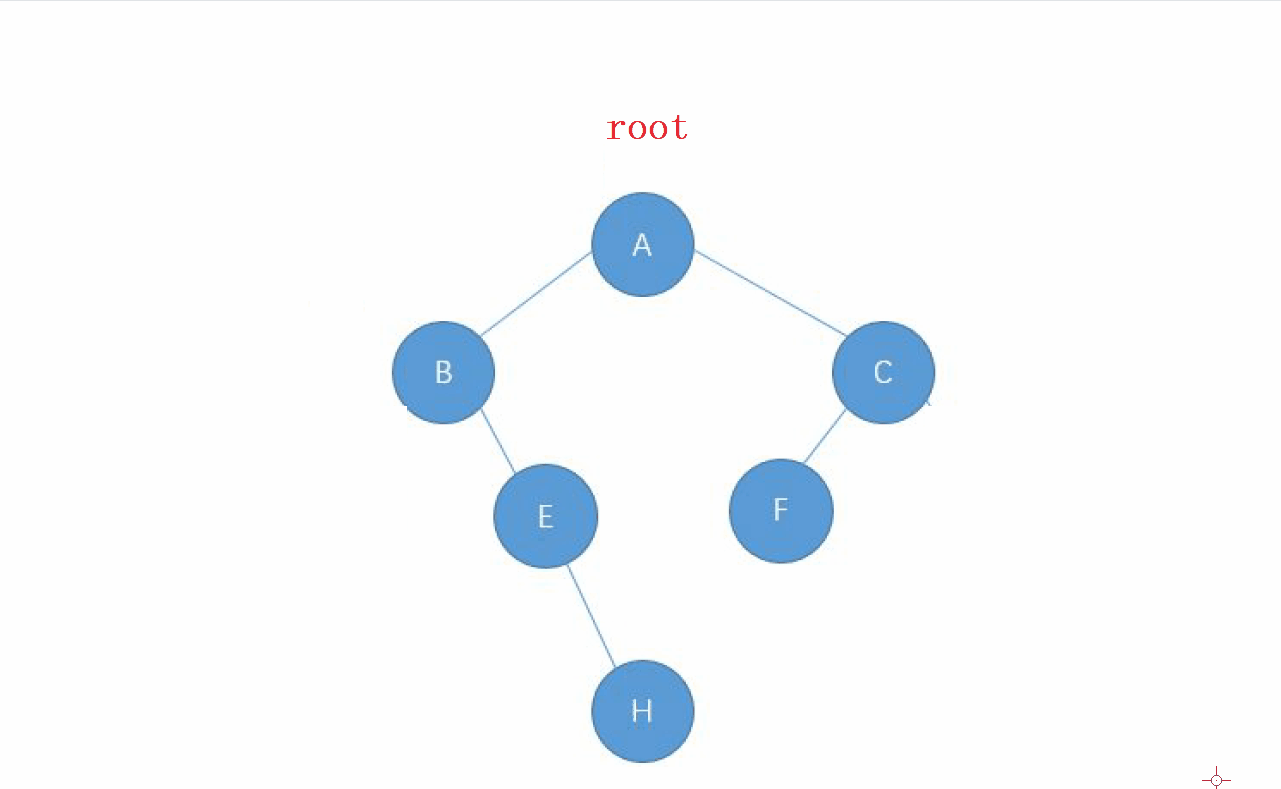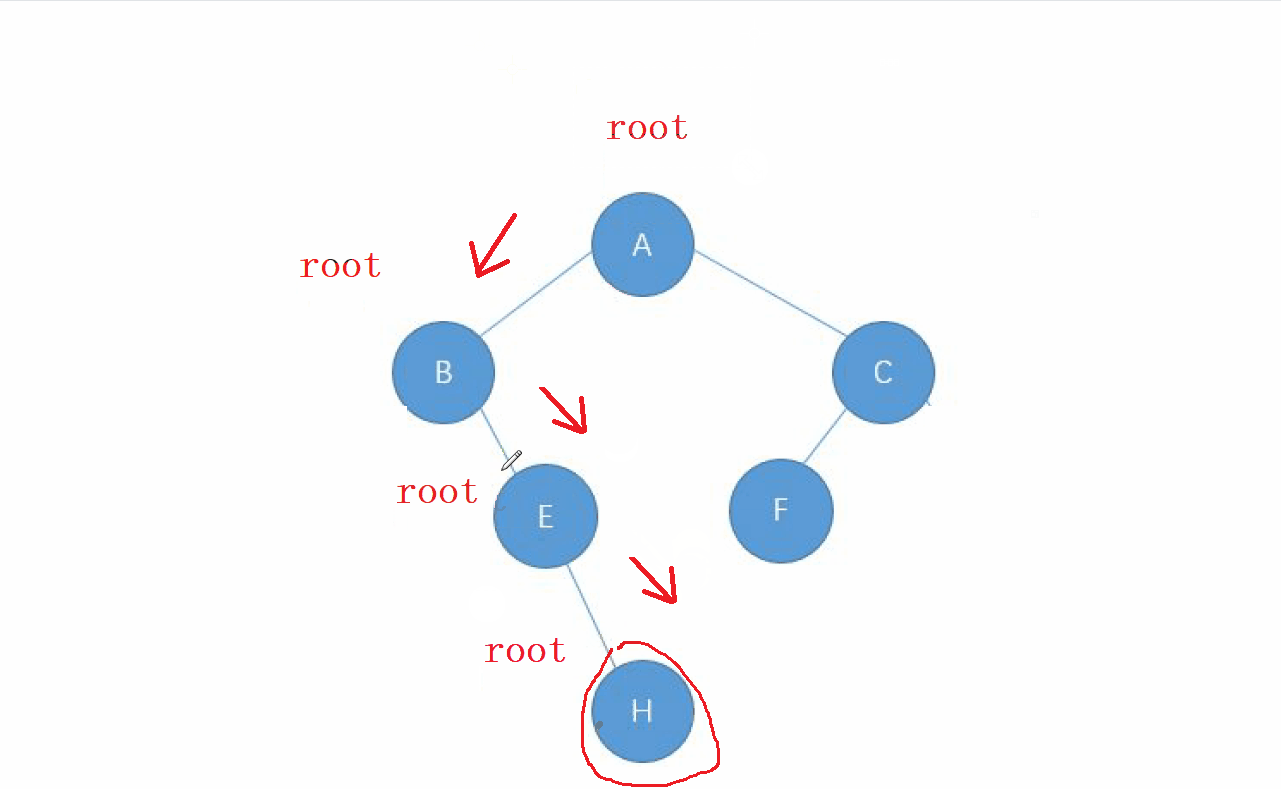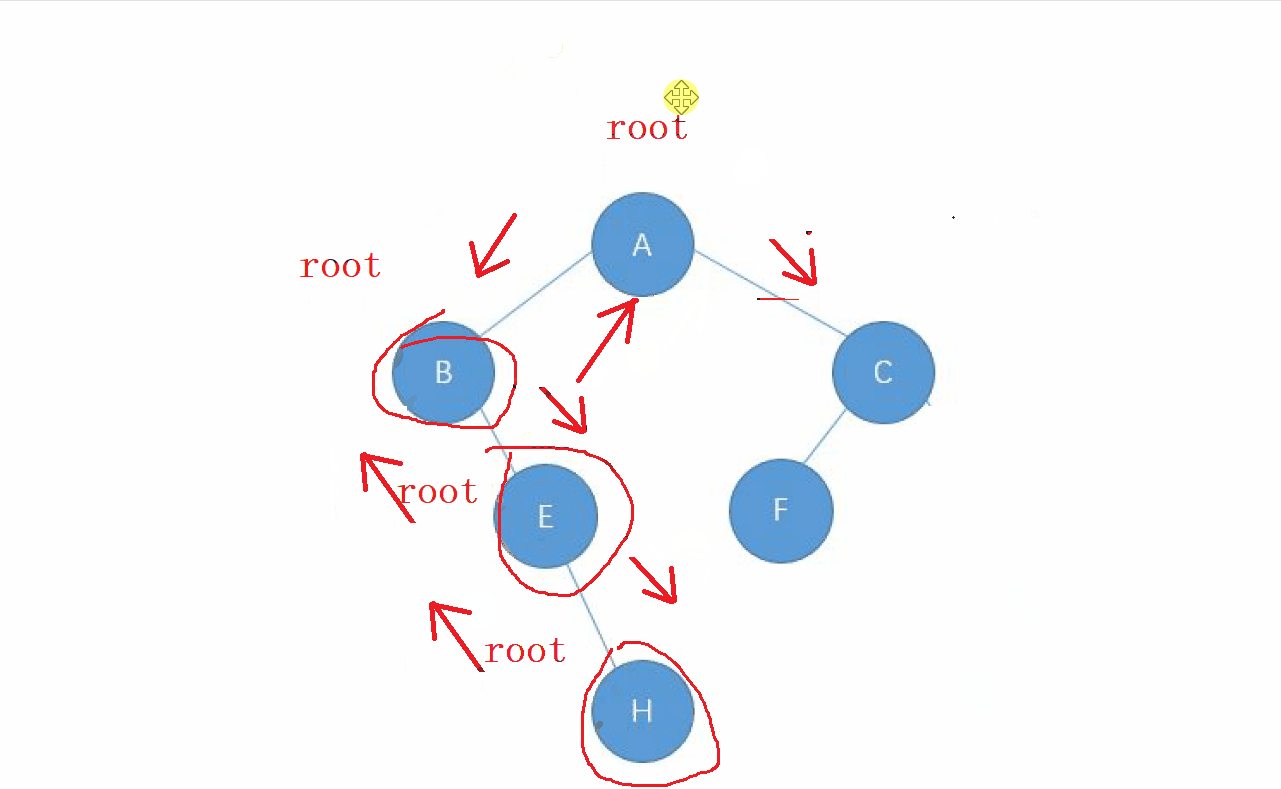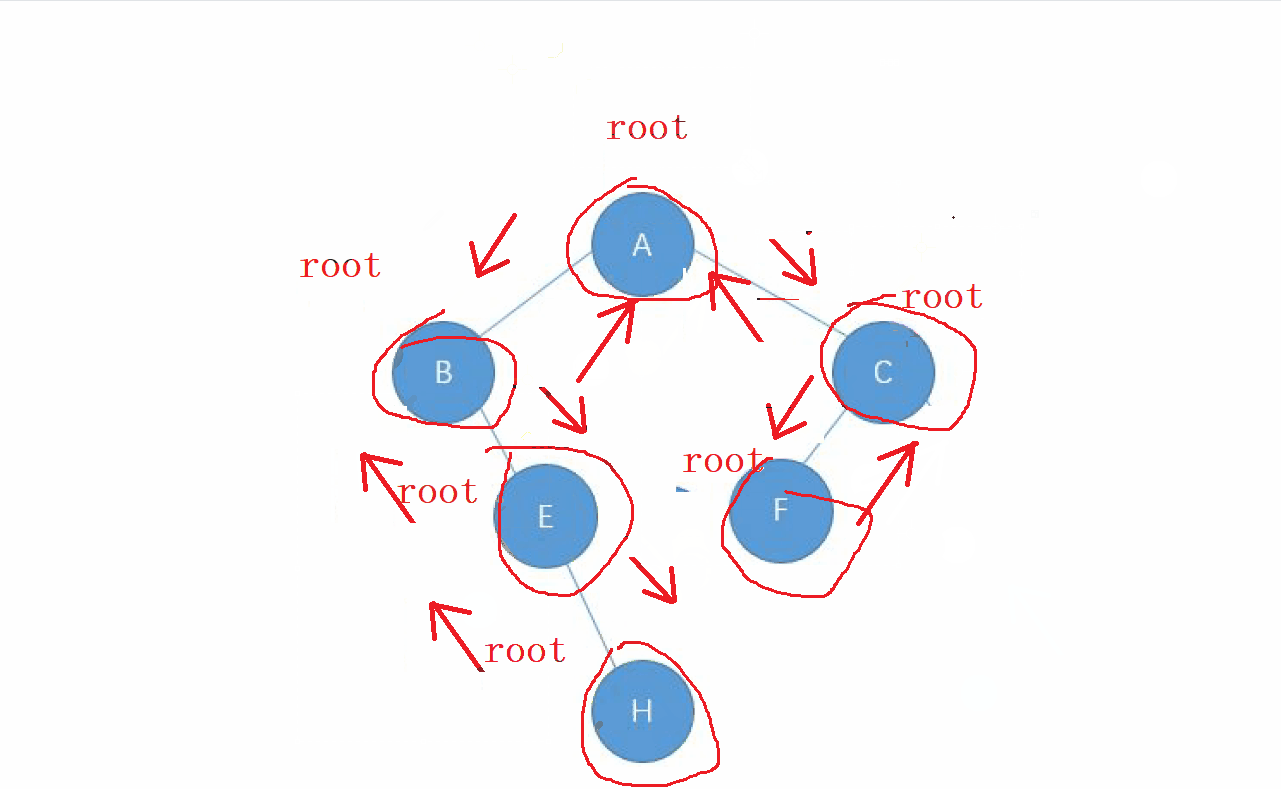
1. 后序遍歷的特點

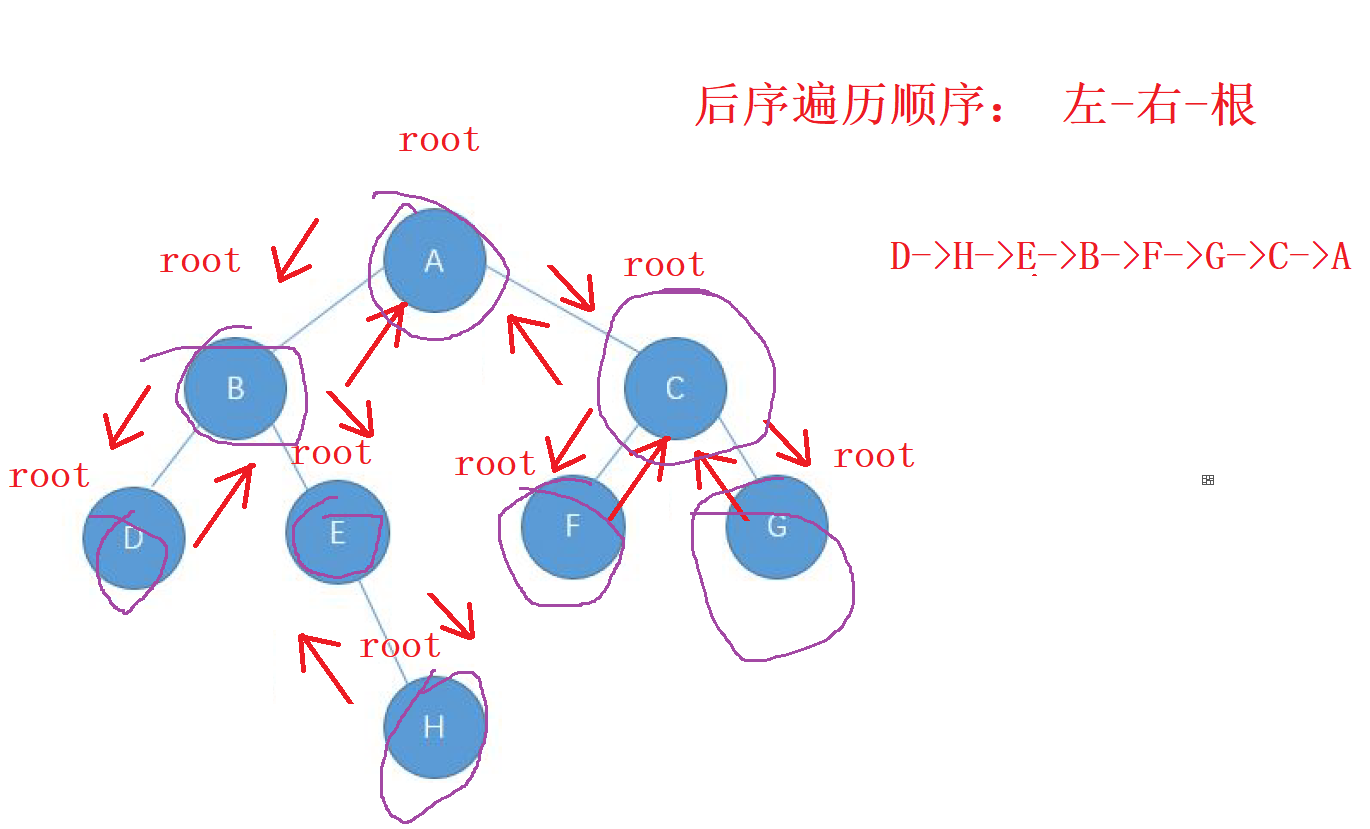
后序遍歷的順序就是 ： 左-右-根 的順序，

還是先走左邊的節點，讓 左邊的節點 成為 新的根 ， 直到找到走完整個 左子樹 ，回退后繼續走 右子樹，當 右子樹走完之后，回去的根節點就是我們要 訪問 的

動畫演示

2. 后序遍歷的實現

<1>. 后序遍歷的遞歸實現

   // 后序遍歷public void lastDisplay(TreeNode root) {if (root==null) {return;}lastDisplay(root.left);lastDisplay(root.right);System.out.print(root.val+" ");}

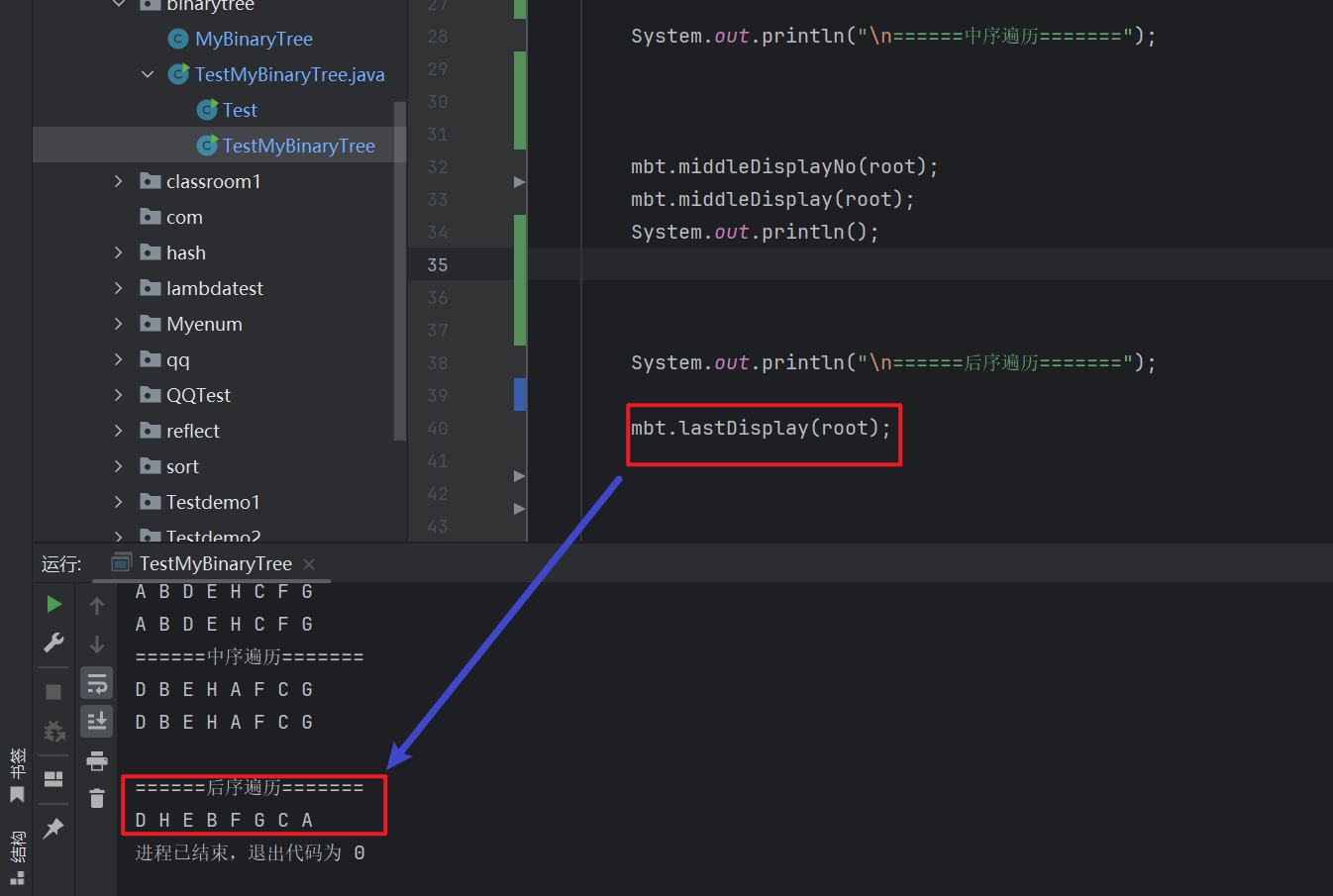
這里的代碼的遞歸思路就是完美的按照我們遍歷方向來的， 先遞歸，后訪問 ，小編在這里就 不贅述 了

<2>. 后序遍歷的非遞歸實現

 // 非遞歸的后序遍歷public  void  lastDisplayNo (TreeNode root) {Stack<TreeNode> stack=new Stack<>();TreeNode cur=root;TreeNode flg=null;while (cur != null || !stack.empty()) {while (cur != null) {stack.add(cur);cur=cur.left;}TreeNode top=stack.peek();if (top.right == null || flg==top.right) {System.out.print(top.val+" ");flg=top;stack.pop();} else {cur=top.right;}}System.out.println();}

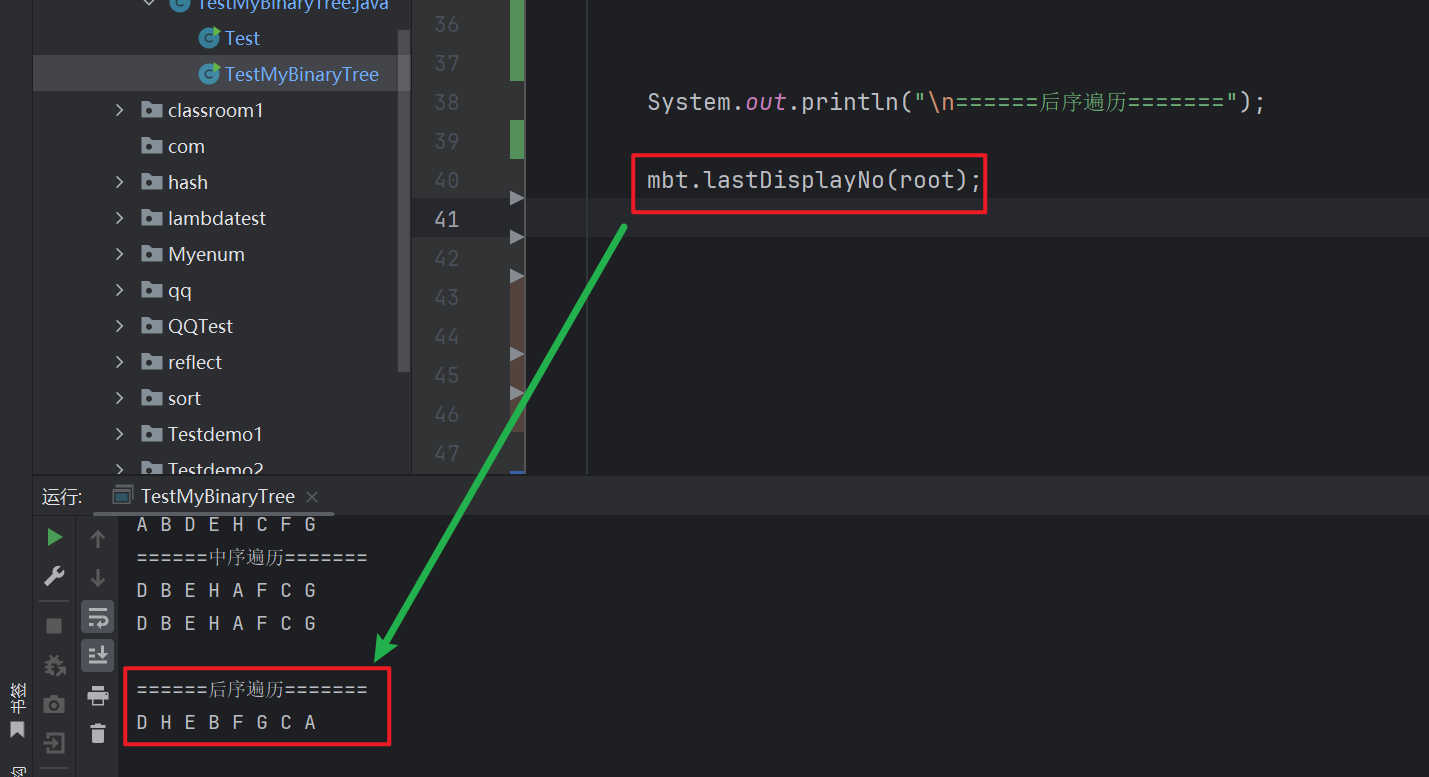
非遞歸的實現思路：

我們先定義一個棧，用來存放節點， 而這里存放的節點有可能是 左子樹的節點，也有可能是 右子樹的節點

1. 先向左走，讓左子樹的節點先入棧

2. 然后 查看棧頂元素，如果棧頂元素的右節點 為 null ， 我們就 打印（訪問） 該節點，

3. 如果棧頂元素的 右節點 不為 null , 我們就 讓 該節點 向右走 , 并且入棧

4. 以此循環往復，當 棧為 null 并且 節點 cur 也為 null ， 說明我們已經遍歷完這個 二叉樹所有的節點

魚式瘋言

無論是 非遞歸還是遞歸實現 對二叉樹的 后序遍歷

• 小伙伴們只需要記住一點： 后序遍歷 一定是 兩邊先走完 ,最后回到我們的根節點才 訪問 的

• 小伙伴們一定要把每個節點都看出一顆獨立的樹。每個節點 都是一個 獨立的根節點 來理解我們的 三大遍歷

TreeNode flg =nullif (top.right == null || flg==top.right) {System.out.print(top.val+" ");flg=top;stack.pop();} 

細節處理： 我們需要用一個 flg 來記錄上一個已經 訪問過 的節點，判斷 是否訪問過， 防止再次讓 top 向右走，繼續入棧， 否則會進入 死循環

四. 層序遍歷

談及完前面的 三大遍歷， 這些是我們 操作二叉樹的根本 ，但還有還要介紹一種 比較特殊的遍歷

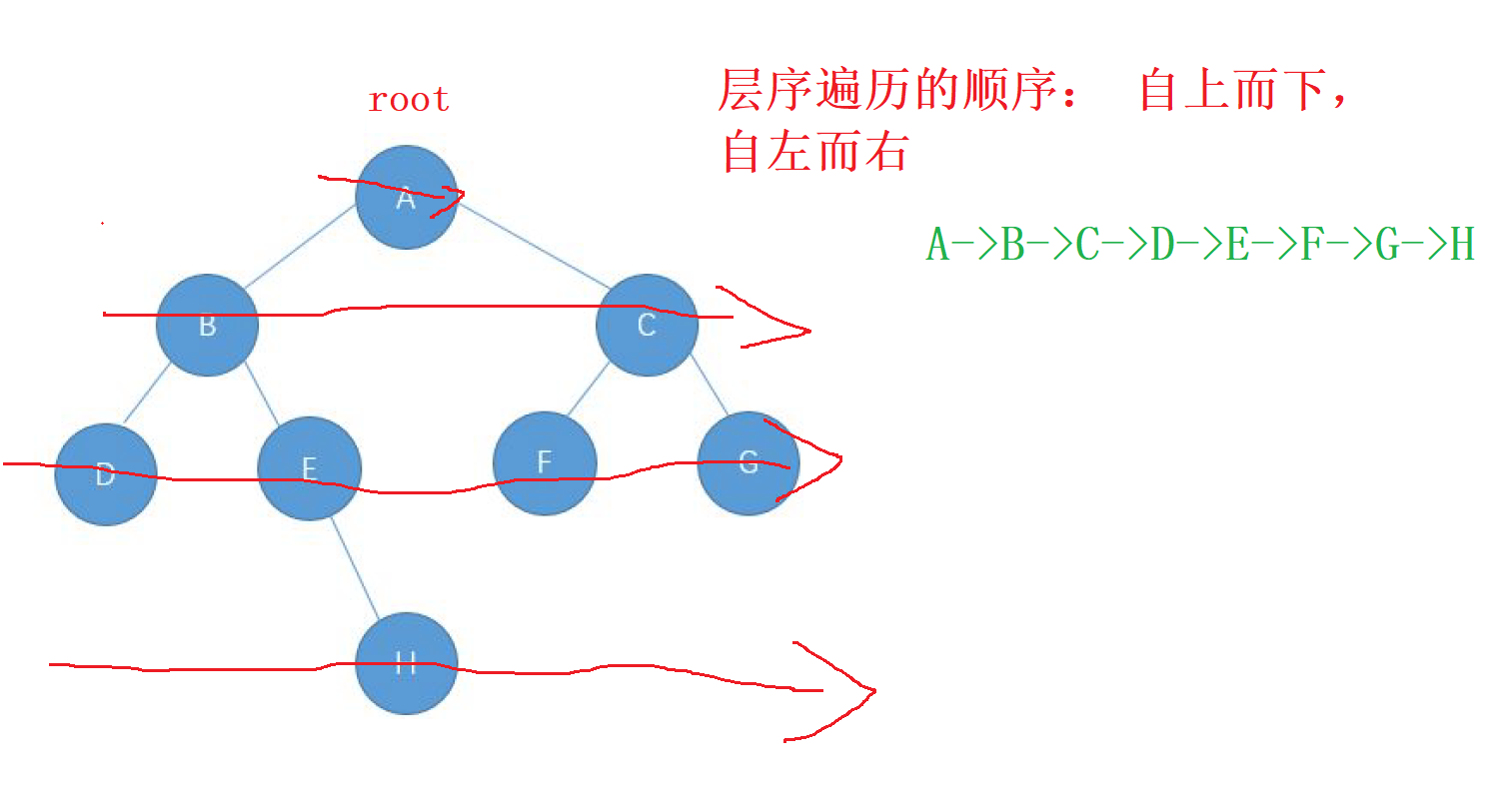
1. 層序遍歷的特點

二叉樹 層序遍歷 的方向是從 根節點，按照 從上而下，從左到右 的順序進行遍歷 二叉樹的每一個節點

動畫演示

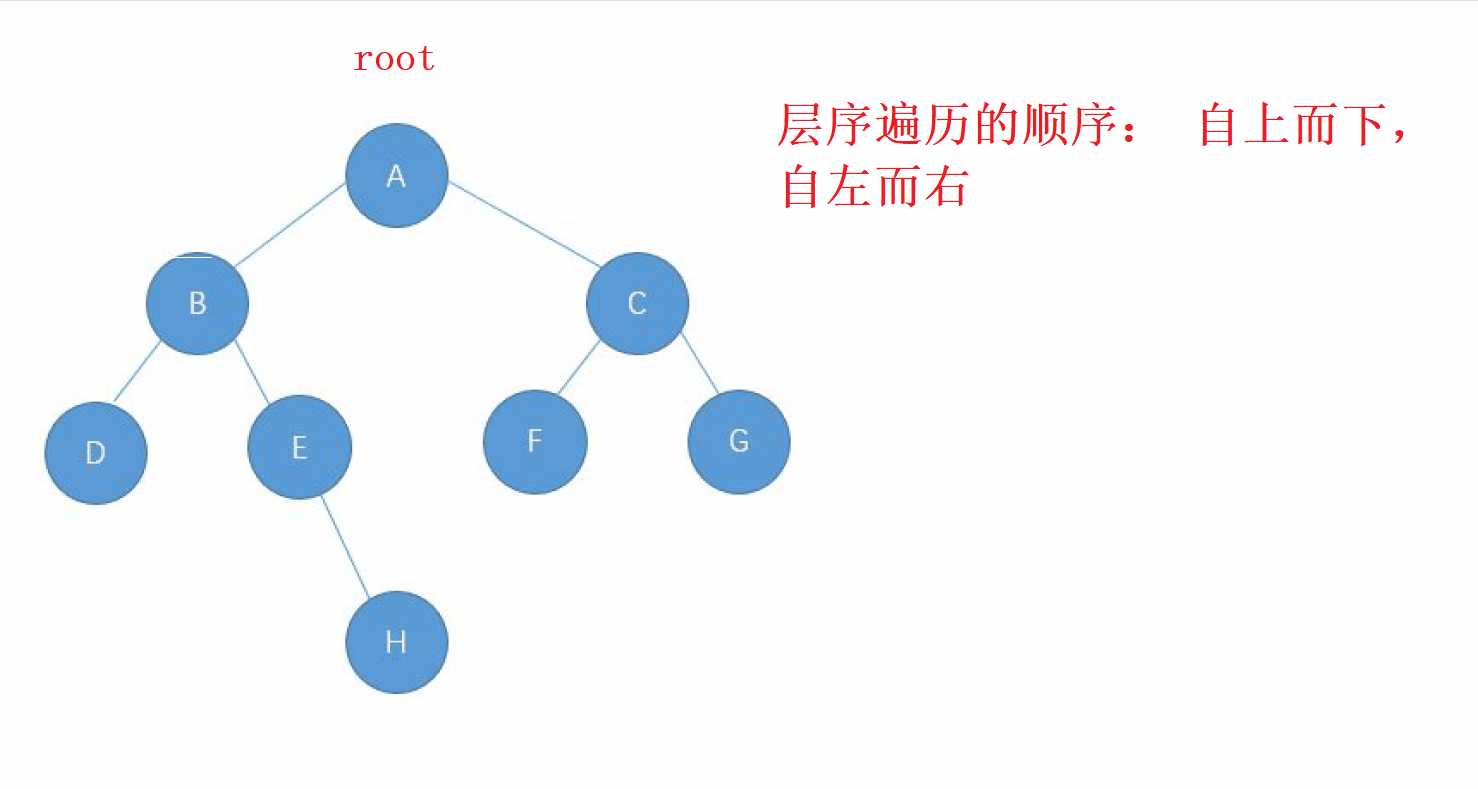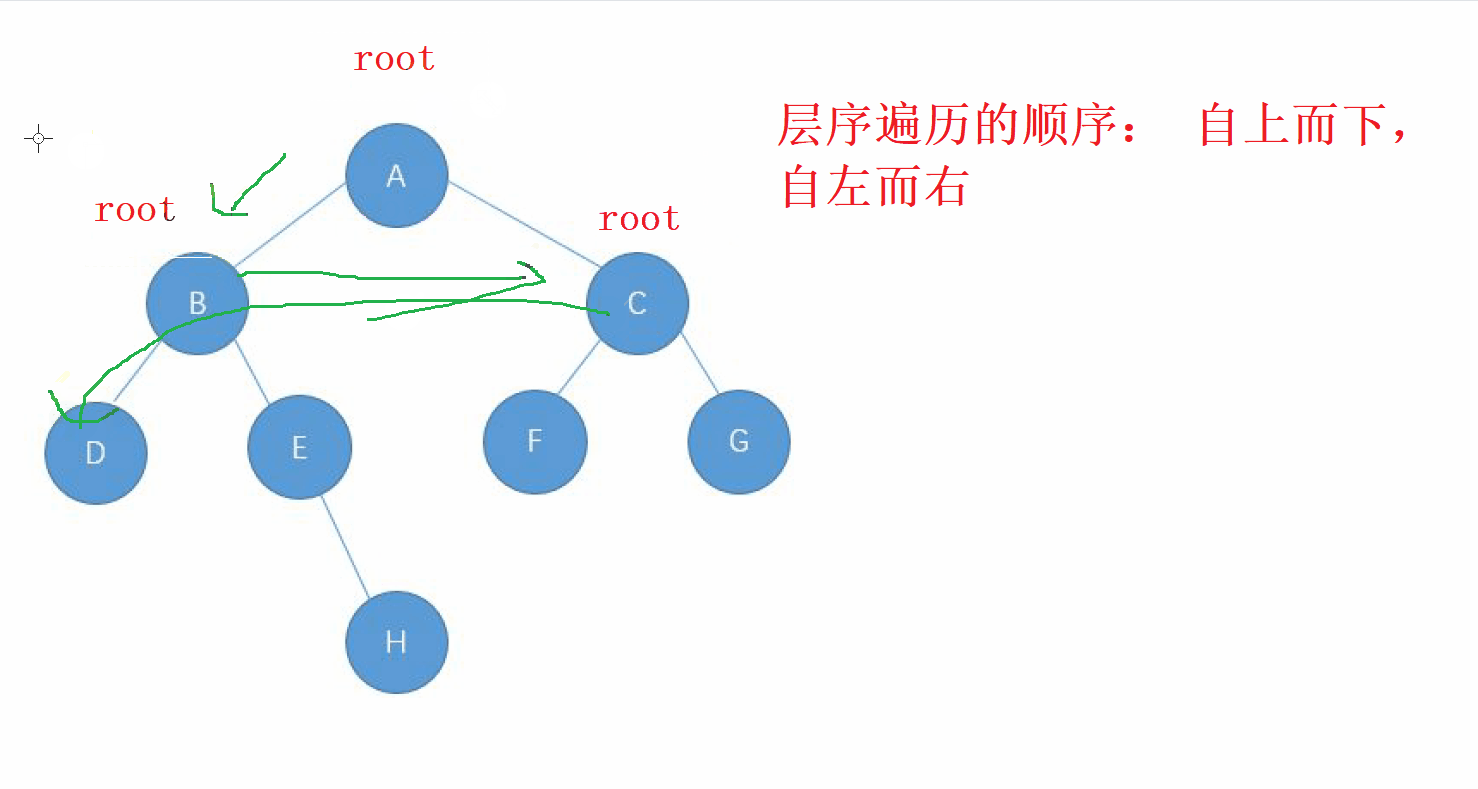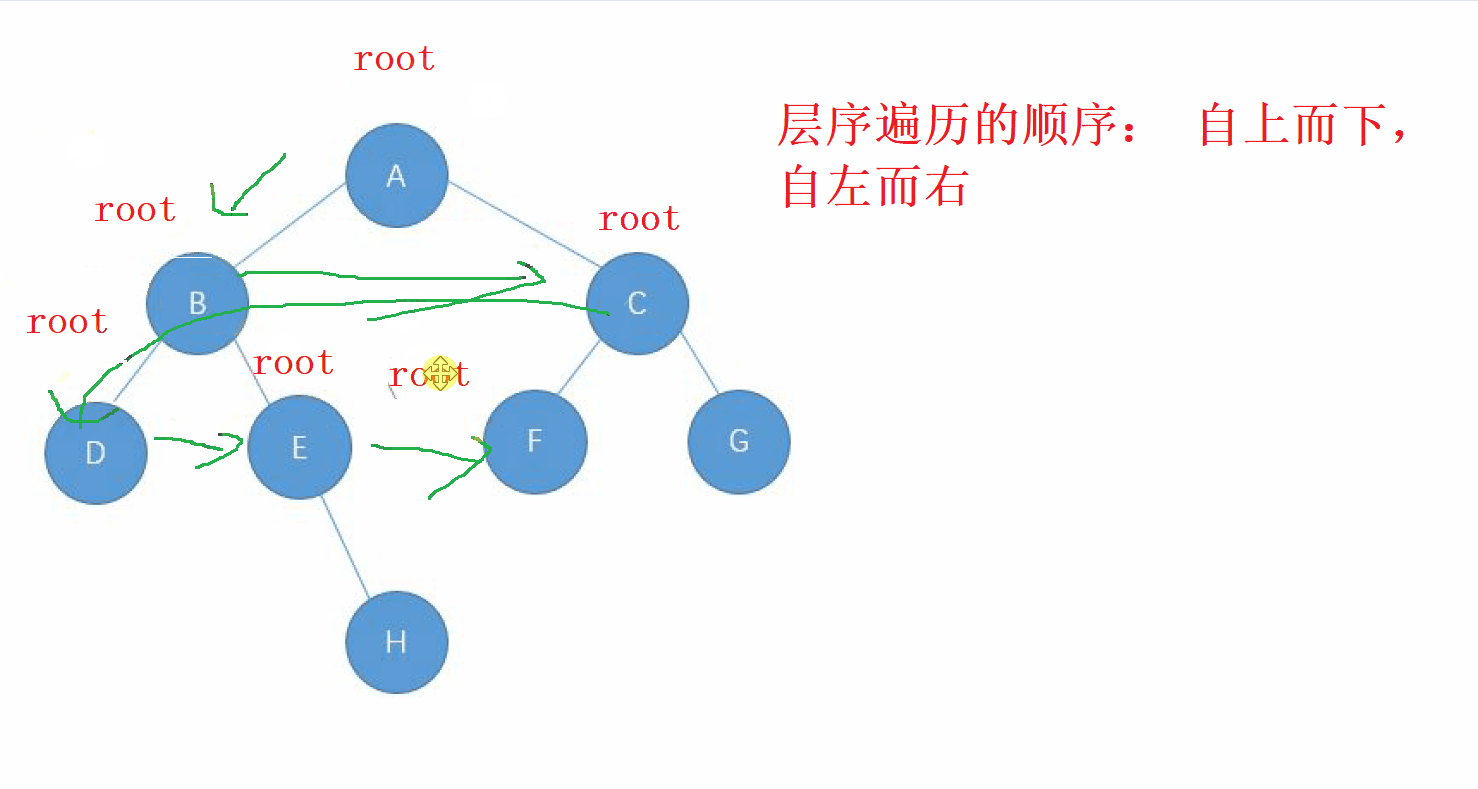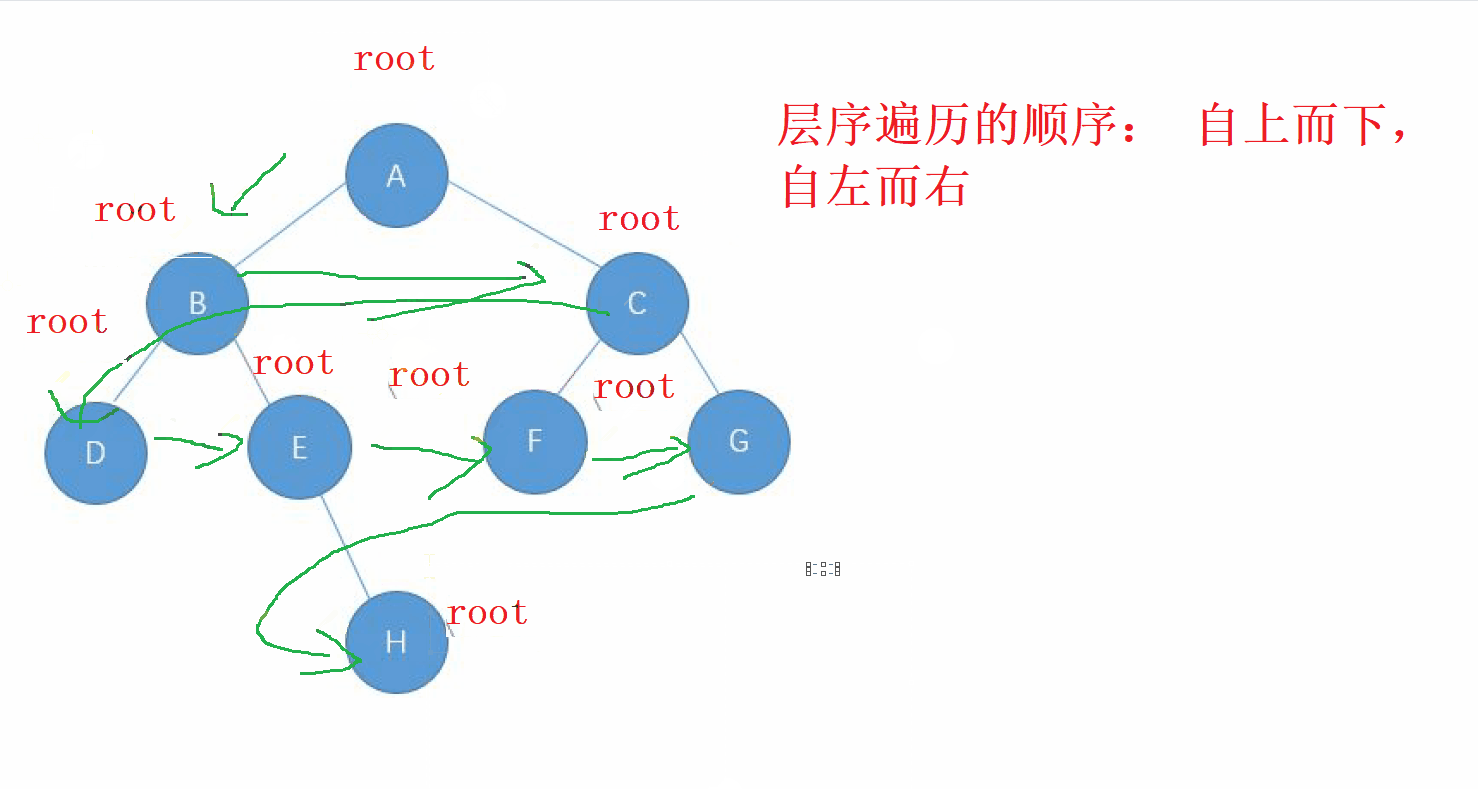
2. 層序遍歷的實現

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/class Solution {List<List<Integer>> S=new ArrayList<List<Integer>>();public List<List<Integer>> levelOrder(TreeNode root) {if(root==null) {return S;}creatOrder(root,0);return S;}public void creatOrder(TreeNode root,int i) {if(root==null) {return ;}if(S.size()==i) {S.add(new ArrayList<Integer>());}S.get(i).add(root.val);creatOrder(root.left,i+1);creatOrder(root.right,i+1);}
}

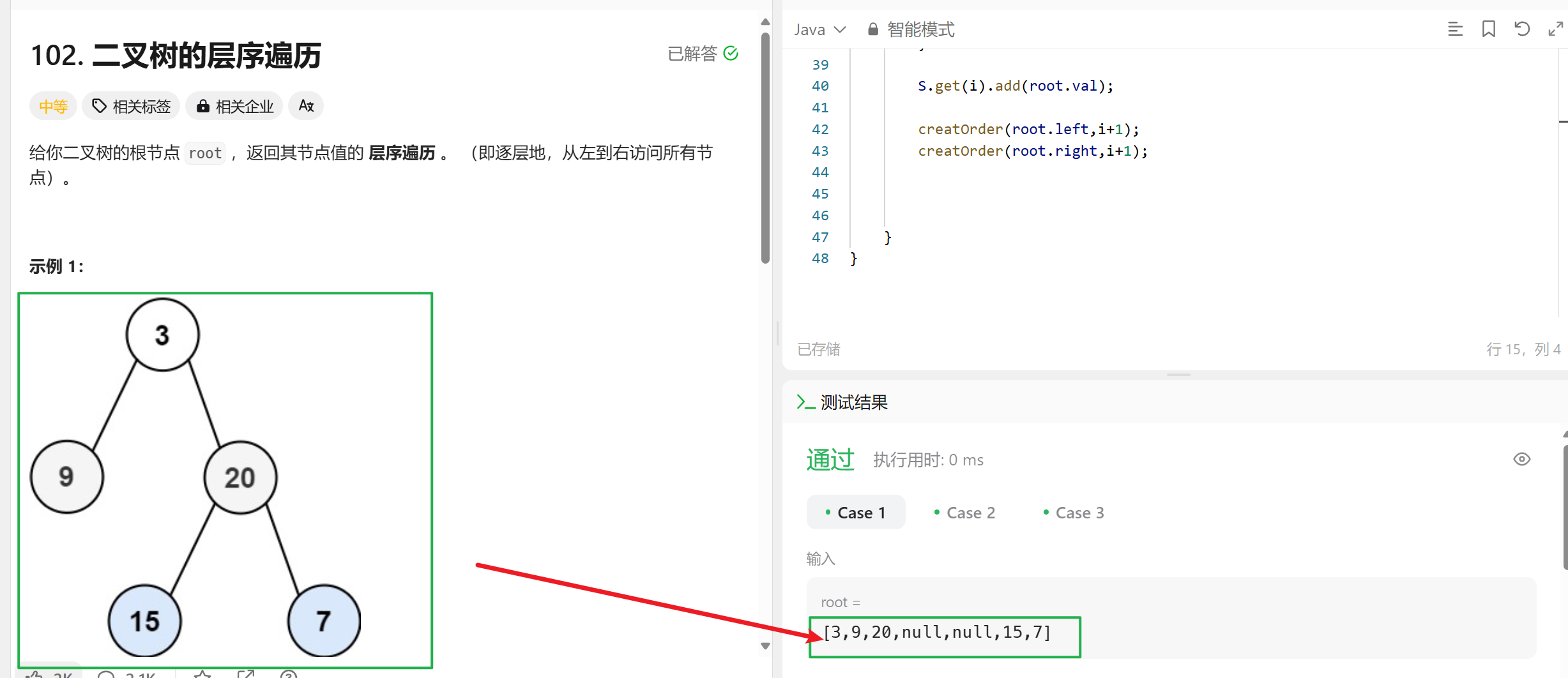
具體實現步驟：

1. 我們用一個 二維數組（二維順序表） 來存儲每一個節點，二叉樹 每一層代表是二維數組的 每一行， 在這二叉樹每一層的行中，從左往右的節點 代表二維數組的 每一列

2. 當二叉樹從 左子樹 開始遞歸， 意味著先存儲 每一行 的 二叉樹的節點

3. 當二叉樹向 右子樹 開始遞歸， 意味著存儲 每一列 的 二叉樹的節點

4. 最終當整個二叉樹完全遞歸就意味著 全部的節點都存儲在 這個二維數組 (二維順序表) 中

魚式瘋言

  if(S.size()==i) {S.add(new ArrayList<Integer>());}

細節處理

每新添加 一行數據 ，需要 擴容 ，就是需要再 實例化一個順序表 ，已有的行數就 不需要了

小伙伴們有沒有發現，二叉樹的層序遍歷，本質上和我們的 完全二叉樹的定義 是一樣的，都是滿足 自上而下，自左而右 的特點

六. 二叉樹遍歷的應用

學習完了 二叉樹遍歷，小伙伴們是時候 牛刀小試 一下了 💞 💞 💞

1. 習題一：

1.某完全二叉樹按層次輸出（同一層從左到右）的序列為 ABCDEFGH 。該完全二叉樹的前序序列為()

A: ABDHECFG

B: ABCDEFGH

C: HDBEAFCG

D: HDEBFGCA

題目解析

我們知道了二叉樹的 層序遍歷 , 并且小伙伴們還有沒有注意一個條件就是 完全二叉樹

完全二叉樹的特點就是 自上而下 ， 自左而右 節點不間斷

那么我們不妨畫個草圖吧

畫出草圖，我們就很明顯的知道了，答案選： A

2. 習題二：

2.二叉樹的先序遍歷和中序遍歷如下：先序遍歷：EFHIGJK;中序遍歷：HFIEJKG.則二叉樹根結點為()

A: E

B: F

C: G

D: H

題目解析：

此題題目就是 答案， 我們知道前序遍歷， 是從 根節點 開始的 , 所以 第一個訪問出來的節點 就是我們的 根節點

故：答案選：A

3. 習題三：

3.設一課二叉樹的中序遍歷序列：badce，后序遍歷序列：bdeca，則二叉樹前序遍歷序列為()

A: adbce

B: decab

C: debac

D: abcde

題目解析：

此題的精髓就在于，我們要根據 中序遍歷 和 后序遍歷 ，畫出草圖， 根據草圖得到我們的 前序遍歷

畫草圖的方法：

方法： 先根據后序遍歷尋找 根節點

對于 后序遍歷 來說：根節點是從右往左 ， 然后結合 中序遍歷的特點 來確定 左右節點 的位置

故此題答案選: D

4. 習題四：

4.某二叉樹的后序遍歷序列與中序遍歷序列相同，均為 ABCDEF ，則按層次輸出(同一層從左到右)的序列為()

A: FEDCBA

B: CBAFED

C: DEFCBA

D: ABCDEF

題目解析 :

此題的精髓就在于，我們要根據 中序遍歷 和 后序遍歷 ，畫出草圖， 根據草圖得到我們的 層序遍歷

依照上一題的方法，我們成功畫出草圖，最終得到我們的層序遍歷

故答案選: A

魚式瘋言

獨家秘方：

1. 對于我們已知 前序和中序 遍歷，我們的方法就是根據 前序遍歷從左往右 找根節點，然后結合 中序遍歷 畫出草圖

2. 對于 我們已知的 后序和中序 遍歷， 我們的方法是 根據 后序遍歷 從右往左找根節點 ， 然后結合中序遍歷 畫出草圖

對于上述題目來說， 畫圖是 根本

總結

• . 二叉樹的遍歷初識： 我們通過基本的概念知道了二叉樹是通過一定 規則和方向 來遍歷我們 每一個節點

• . 前序遍歷 : 本源是 根-左-右的方向遍歷

• . 中序遍歷： 本源是 左-根-右的方向遍歷

• .后序遍歷 ： 本質上還是根據 左-右-根的方向遍歷

• . 層序遍歷： 遵循一個 自上而下， 自左而右 的順序遍歷

• . 二叉樹遍歷的應用 ： 我們主打一個對于這四種遍歷的性質的理解和應用，來畫圖解題

如果覺得小編寫的還不錯的咱可支持 三連 下 (定有回訪哦) , 不妥當的咱請評論區 指正

希望我的文章能給各位寶子們帶來哪怕一點點的收獲就是 小編創作 的最大 動力 💖 💖 💖