Slepian Spectral Estimator(1950)

做譜估計的目標是盡可能看清楚信號功率譜在某一個頻率上的情況，假設我們想了解零頻時的分布，最理想的情況是濾波器的傳遞函數H(ω) 是一個沖激函數，這樣就沒有旁瓣，也就沒有泄漏；其次，主瓣寬度為零，分辨率極好。然而在現實中，理想的沖激函數是無法實現的，所以，只能允許H(ω) 有一定通帶（假設為-βπ,βπ ）。另外，由于濾波器是有限長度的，所以H(ω) 不可避免地會有泄漏，但我們可以要求泄漏盡可能地小，即做下面的優化

時，有最優解，其中U是矩陣B的特征向量，而h正是B最大特征值對應的那個特征向量。

小結

與傳統的周期圖譜估計方法相比，Slepian Spectral Estimator將著眼點轉移到要觀察的頻率點附近，其目標是，設計一個對信號功率譜進行估計的濾波器，希望信號通過濾波器后，想要的頻譜分量能夠有效保存下來，而無關的譜分量盡可能被抑制。?????? 這種估計存在的問題：

1. 僅考慮濾波器自身的響應，而沒有考慮信號，不同的信號通過濾波器會有不同的表現，特別是隨機信號會特別復雜。這種譜分析是信號無關的，不管信號是什么樣的，都使用同一個濾波器進行估計。
2. 沒有用到統計的觀念，所有的信息都是確定的，只依賴于頻帶的寬度。然而對隨機信號進行譜估計是，不能不用到統計。

Capon Spectral Estimator (1969)

與一般譜估計的對比

小結

????????傳統的譜分析：為了獲得信號在某個頻率點上能量情況，就極大化信號在這個頻率點上的響應，Slepian方法就是典型代表：在要分析的頻率的附近劃一個區域，然后極大化信號在這個區域上的響應，盡可能抑制其它頻率的響應。而Capon方法的思路是，在要觀察的頻率點上給定一個約束條件，使信號在這個頻率上的響應得到保證，然后在此基礎上提出新的要求：極小化信號在其它頻率的響應。

MUSIC（Multiple Signal Classification）

MUSIC

至此，我們可以看到MUSIC方法至少在3個方面進行了創造性的工作：

·1. 對Y求相關陣，充分考慮了噪聲

·2. 在解方程很困難的情況下，放棄了直接求解方程的方法，而是分析等式兩端的秩，這樣雖然不能完全得到方程的解，但是我們感興趣的信息（信號頻率）可以得到。

·3. 得到了信號子空間和方向矢量構成的子空間相同，進而得到方向矢量張成的子空間與噪聲子空間正交的結論，這也是MUSIC方法的核心所在。

小結

MUSIC方法提出了“超分辨率”的理念，首次呈現了分辨率極高的譜圖。在之前的譜分析中，分辨率取決于信號的長度，信號越長，分辨率越高。而在MUSIC方法中，分辨率和信號長度沒有太大關系，以很短的數據就可以獲得很高的分辨率，能得到這種效果的原因主要有2個：

·1. MUSIC是一種非線性方法，它脫離了過去用線性濾波提取頻率分量的傳統路線，因此它達到的水平是Slepian和Capon等方法無法相比的。

·2. MUSIC得到的是一種“偽譜”，譜峰的位置代表信號的頻率，但高度并不代表信號在這個頻率上的能量大小，而且這種方法也沒有給出譜峰高度與信號能量之間的關系。

MUSIC譜是一種“偽譜”，只反映了方向矢量與噪聲子空間之間的正交關系的良好程度。在理想情況下，它們之間應該是嚴格正交的，但是因為噪聲的存在，譜圖只反映了它們之間關系的一種估計。

?????? 在上面的5步中，最困難的是第3步，因為有些時候無法準確地對特征值分組，如果分組不準，會對MUSIC性能造成致命的影響，因為特征分組錯誤，就意味著子空間估計錯誤，信號頻率分量的個數也會估計錯誤。因此MUSIC是一種很脆弱的方法，這種方法對信噪比的要求特別高，只有在高信噪比的條件下，才能準確估計子空間的維數。在信噪比的條件下，周期圖估計效果比較好，通常我將MUSIC和周期圖兩種方法結合使用：先用周期圖法確定信號個數，然后在用MUSIC方法獲取信號頻率分量準確位置。

ROOT MUSIC

Min-Norn MUSIC

MUSIC的核心是方向矢量子空間與噪聲子空間正交。從正交性出發，容易導致“偽峰”的出現。因為在尋找正交點的過程中，頻率點在整個頻率軸上滑動，方向矢量與噪聲子空間的關系在不斷變換，在某一頻點兩者正交時，我們判定這個頻點就是我們希望得到的頻點之一，即這個頻點包含在信號中。然而我們僅僅知道正交時，該頻點在信號中，那么不正交時有什么意義呢？或者說兩者之間的夾角的大小有什么意義呢？兩者之間的夾角為89度時是不是比60度更像信號呢？MUSIC方法并沒有給出上面問題的答案。

那么能不能構造一種新的方法，既能利用MUSIC帶來的超分辨率，又能引入誤差的概念，作為頻點與信號符合程度的判定依據呢？答案就是使用Min-Norm MUSIC方法。

小結

MUSIC方法最核心的思想是：方向矢量張成的子空間和信號矢量張成的子空間是同一個子空間，判斷2個子空間是否相同時很困難的，尤其是兩個子空間對應的基不相同的時候。在這里，信號子空間的基使彼此正交的，但是方向子空間的基并不正交，為了得到信號頻率的信息，必須讓兩個子空間產生關系，所以前面提出了很多必要條件，Min-Norm MUSIC 對譜峰的高度做出了解釋。

MUSIC與Capon方法比較

ESPRIT(Estimation of Signal Parameters with Rotation Invariant Technique)用旋轉不變技術估計參數

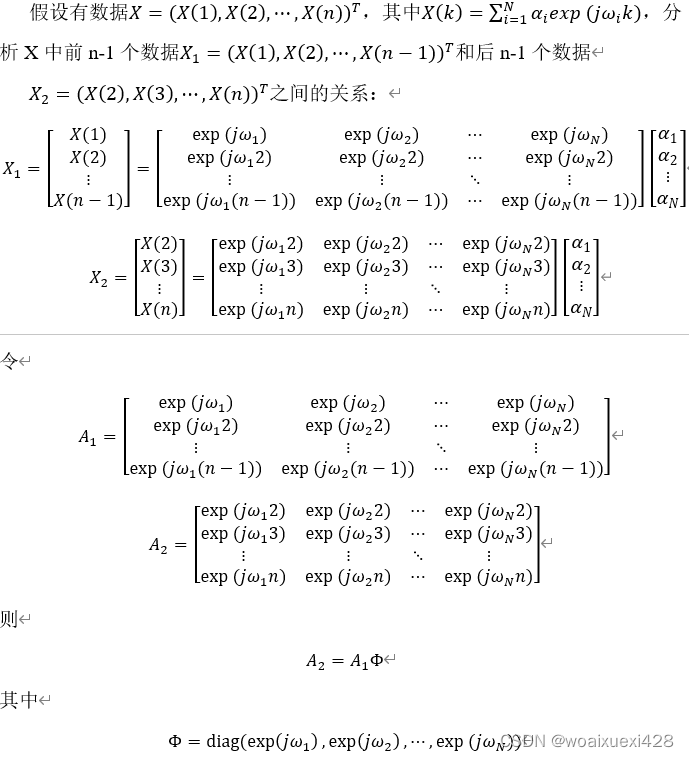
ESPRIT方法可以一次求出我們想要的所有信號頻點。

------------------------------------------------------------------------------------------------
因為文檔中公式較多，不方便編輯，所以本文使用截圖的方式展現。如需電子版文檔，可以通過下面的鏈接進行下載。

鏈接http://generatelink.xam.ink/change/makeurl/changeurl/11779