理論

方差分析（ANOVA, Analysis of Variance）是統計學中用來比較多個樣本均值之間差異的一種方法。它通過將總變異分解為不同來源的變異來檢測因子對響應變量的影響。方差分析廣泛應用于實驗設計、質量控制、醫學研究等領域。

方差分析的基本模型

方差分析的基本模型可以用以下形式表示：

單因素方差分析

單因素方差分析（One-Way ANOVA）是最簡單的形式，用于比較一個因素的多個水平對結果的影響。例如，比較不同肥料對作物生長的影響。

步驟：

1.假設檢驗：

2.計算組間方差和組內方差：

組間方差（MSB，Mean Square Between groups）：

組內方差（MSW，Mean Square Within groups）：?

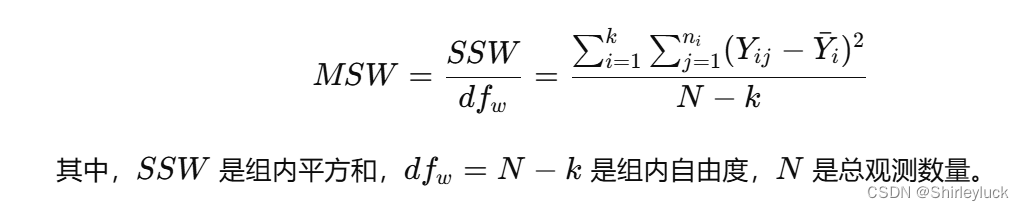
3.計算F值：

4.查找臨界值：

5.做出決策：

如果計算得到的F值大于臨界值，則拒絕原假設，說明組間均值存在顯著差異。

如果計算得到的F值小于等于臨界值，則不拒絕原假設，說明組間均值不存在顯著差異。

多因素方差分析

多因素方差分析（Two-Way ANOVA 或 Factorial ANOVA）用于同時研究兩個或多個因素對結果的影響，且可以考察因素間的交互作用。例如，研究不同肥料和不同灌溉方式對作物生長的聯合影響。

方差分析的假設條件

1. 獨立性：各組別的觀測值相互獨立。
2. 正態性：各組別的觀測值服從正態分布。
3. 方差齊性：各組別的方差相等。

如果數據不符合這些假設，方差分析的結果可能會失真，因此進行正態性檢驗可以幫助我們評估模型的適用性。

在進行正態性檢驗時，我們主要關注檢驗的 p 值。如果 p 值較大（通常大于 0.05），則表明數據符合正態分布的假設，可以繼續進行方差分析。如果 p 值較小，則可能需要考慮使用非參數方法或對數據進行轉換以滿足模型假設。

實際應用中的考慮

在實際應用中，必須確保滿足方差分析的假設條件，否則結果可能不可靠。當假設條件不滿足時，可以考慮使用非參數檢驗（如Kruskal-Wallis檢驗）或調整模型（如方差不齊的情形下使用Welch's ANOVA）。

結論

方差分析是一個強大的統計工具，可以有效地檢測多個組別之間的差異。然而，應用時需要謹慎，確保數據符合基本假設，并在必要時進行模型調整或采用其他統計方法。隨著統計學的不斷發展，方差分析的方法和應用也在不斷進步，研究人員需要不斷更新知識，以便在復雜的實際問題中作出準確的判斷。

R語言實操-方差分析模型

方差分析（ANOVA）模型用于比較多個組之間的均值是否有顯著差異。進行方差分析模型，最好對數據進行正態性檢驗。正態性檢驗有助于確認方差分析模型的假設是否滿足，特別是方差分析對數據的正態性有一定的要求。寫了另一篇關于正態性檢驗的文章：

5.22 R語言-正態性檢驗-CSDN博客文章瀏覽閱讀66次，點贊2次，收藏4次。正態性檢驗的目的是確定一組數據是否符合正態分布（也稱高斯分布）。在統計分析和數據建模中，正態性假設是許多統計方法和模型的基礎。了解數據是否符合正態分布有助于選擇適當的統計方法和確保分析結果的有效性。本文主要從方面來進行正態性檢驗。即假設檢驗的角度來說，數據是否服從正態分布可以通過與“”這樣一個零假設進行假設檢驗計算，構建相關統計量來計算出檢驗結果。文中提及的Q-Q Plot是正態檢驗 (Normality Test)——常見方法匯總與簡述-CSDN博客。https://blog.csdn.net/Shirleyluck/article/details/139131768?spm=1001.2014.3001.5501https://blog.csdn.net/Shirleyluck/article/details/139131768?spm=1001.2014.3001.5501

進行方差分析（ANOVA）模型的步驟：

1. 準備數據：確保你的數據是干凈和適合分析的。

2. 擬合模型：使用 aov 函數擬合方差分析模型。

3. 檢驗模型假設：包括正態性檢驗和方差齊性檢驗。

4. 查看結果：使用 summary 函數查看方差分析的結果

 m = aov(Time ~ IDE, data=ide2)

使用?aov 函數來擬合一個方差分析（ANOVA）模型。具體而言，你正在比較不同 IDE 組別之間的 Time 數據是否存在顯著差異。

• aov(Time ~ IDE, data=ide2): 這行代碼指定模型的公式，即 Time 是因變量，IDE 是自變量。data=ide2 指定了數據來源。
• m = : 這行代碼將擬合的模型賦值給變量 m，以便后續進行模型檢驗和結果分析。

可以使用 summary(m) 來查看方差分析的結果，了解各個組別之間的差異是否顯著。

summary(m) 的輸出通常包含以下部分：

• Df（自由度）：自變量和誤差的自由度。
• Sum Sq（平方和）：自變量和誤差的平方和。
• Mean Sq（均方）：平方和除以相應的自由度。
• F value（F值）：自變量的均方除以誤差的均方得到的F值。
• Pr(>F)（P值）：F值對應的P值，用于判斷顯著性。

# 擬合方差分析模型
m <- aov(Time ~ IDE, data = ide2)# 正態性檢驗
install.packages("nortest")
library(nortest)
shapiro.test(ide2[ide2$IDE == "VStudio",]$Time)
shapiro.test(ide2[ide2$IDE == "Eclipse",]$Time)# 方差齊性檢驗
bartlett.test(Time ~ IDE, data = ide2)
install.packages("car")
library(car)
leveneTest(Time ~ IDE, data = ide2)# 查看方差分析的結果
summary(m)

繪制Q-Q 圖

為了評估方差分析模型（ANOVA）假設的正態性，使用qqnorm和qqline繪制?Q-Q 圖。?Q-Q 圖（Quantile-Quantile Plot）是一種圖形方法，用于比較數據的分布與正態分布。如果數據點大致沿著一條直線分布，則數據可以被認為是正態分布的。

##試試檢驗假設

#首先是正態性假設
# Shapiro-Wilk normality test(夏皮羅-威爾克檢驗)
shapiro.test(ide2[ide2$IDE == "VStudio",]$Time) #H0：研究對象符合正態分布。
shapiro.test(ide2[ide2$IDE == "Eclipse",]$Time)
## 滿足正態性假設

# 但真正重要的是殘差正態性【僅展示】
m = aov(Time ~ IDE, data=ide2) # fit model
shapiro.test(residuals(m)) # test residuals
qqnorm(residuals(m)); qqline(residuals(m)) # plot residuals
## 如果殘差是正態分布的，那么這些點應該近似地落在一條直線上。
## qqline函數在這圖上添加了一條參考線，這條參考線是正態分布的理論分位數線，有助于直觀判斷殘差是否近似正態分布。

# 不正態可以嘗試數據轉換【僅展示】
ide2$logTime = log(ide2$Time) # log transform
View(ide2) # verify

#其次是方差齊性假設 # 方差齊性檢驗就是看兩總體方差是否相等.比如在兩獨立樣本的t檢驗中,兩總體方差1.相等 2.不相等
install.packages("car")
library(car)
leveneTest(Time ~ IDE, data=ide2, center=mean) # Levene's test:用于檢驗兩組及兩組以上獨立樣本的方差是否相等。
leveneTest(Time ~ IDE, data=ide2, center=median) # Brown-Forsythe test: Brown-Forsythe檢驗是指采用Brown-Forsythe分布的統計量進行的各組均值是否相等的檢驗。

##執行獨立樣本T檢驗: 單總體t檢驗是檢驗一個樣本平均數與一個已知的總體平均數的差異是否顯著。
t.test(Time ~ IDE, data=ide2, var.equal=TRUE) #var.equal= TRUE 方差相等
###根據上述結果，可以得出結論：有足夠證據拒絕零假設，接受備擇假設，即Eclipse和VStudio在完成任務所需平均時間上存在顯著差異。
###具體來說，Eclipse組的平均時間比VStudio組多166.05個單位（468.15 - 302.10），并且這個差異是統計上顯著的。