一、說明

???????數學領域有太多有趣的領域，領域我特別感興趣。這是一個奇妙的無限、自我復制的分形世界。更有趣的是分形事物總能在大自然中發現對應物，這對渲染自然界和電腦作圖有更大發揮。分形維度不是整數維，本文對此稍加介紹。

二、分形到底是什么？

分形是一個在任何尺度上看起來或多或少相同的對象。這意味著無論您如何放大分形，細節看起來幾乎相同。

您能給我們舉個例子嗎？我知道這個問題即將到來，所以我畫了一些！這個叫做謝爾賓斯基三角形…

這個叫做龍曲線…

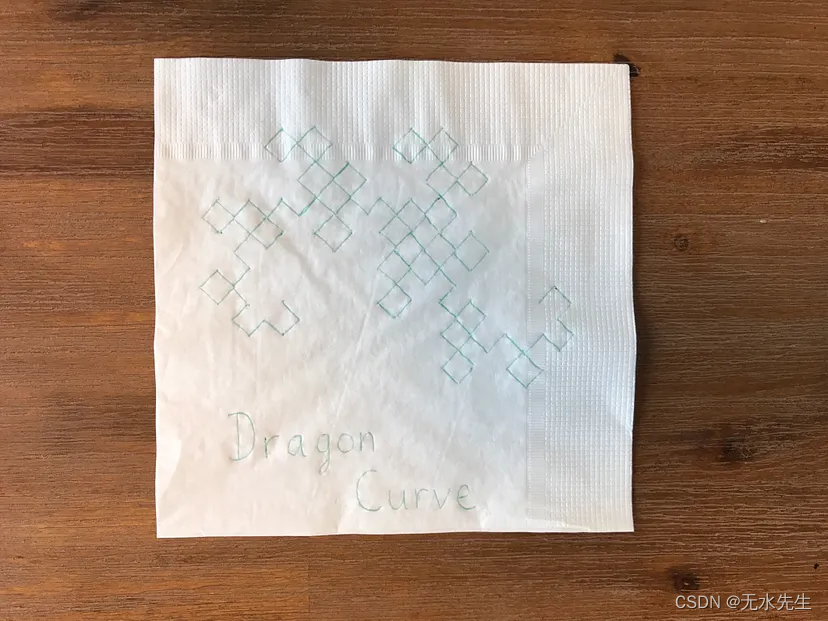
而這個曲線叫做科赫曲線…

我要指出的是，這些都是近似值。實際上，在serviettes上繪制分形是相當棘手的，信不信由你，我無法繪制到無窮小的尺度！所有這些分形都是所謂的自相似分形，這意味著它們的細節在放大時完全相同。這意味著您可以在其內部找到分形的精確副本。

三、更多更深刻的

我喜歡分形的一件事是它們非常直觀。一些分形模式（如上面的例子）非常適合涂鴉，因為它們可以通過遵循迭代過程來構造。

一般來說，自相似分形可以從一些“基塊”構造，方法是將基塊的副本排列在特定的模式中，然后縮小該模式以用作新的“基塊”并重復。（該過程也可以在不收縮的情況下完成，這更容易繪制，但占用的空間越來越大）。

以下是以這種方式繪制的上述曲線的幾個迭代：

當然，任何這樣的構造在你用完空間之前只能進行這么多次迭代，所以物理表示只是真實分形的近似值。然而，如果我們把數學概念一直帶到無窮小，事情就會開始變得有點奇怪。

四、引進無窮小會產生什么樣的怪事？

每當無窮大涉足數學領域時，你都可以期待有一些東西與你的直覺不完全匹配。如果我告訴你分形不符合我們通常的維度概念呢？

對于傳統形狀，我們可以通過使用一定的測量單位測量物體來考慮尺寸，然后使用較小的測量單位重新測量，看看您還得到了多少件。

例如，在這里，我畫了一條線、一個正方形和一個邊長為 1 個“單位”的立方體，然后使用大小為 1/3 的單位重新測量它們。對于直線，現在有 3 = 31 個，對于正方形，有 9 = 32 個，對于立方體，有 27 = 33 個。

?
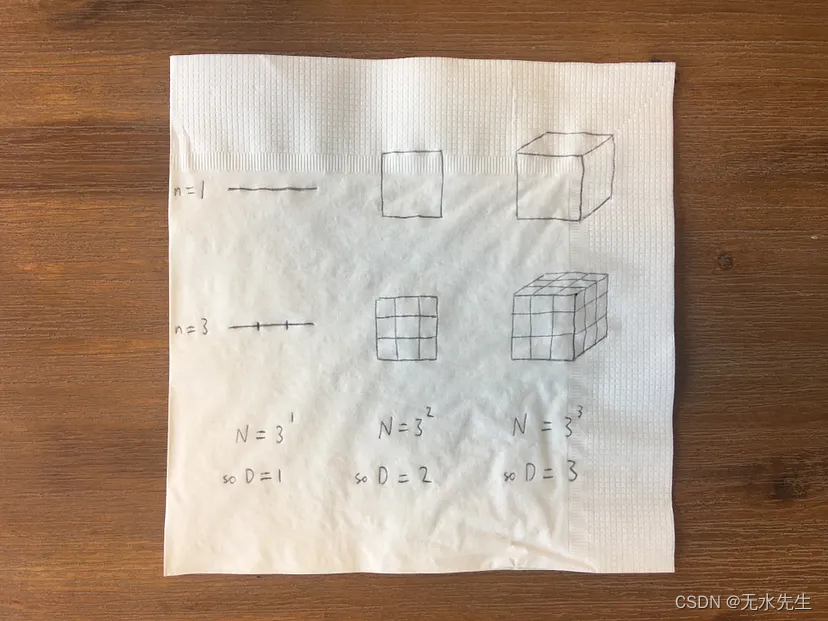
一般來說，如果我們使用大小的 1/n 倍的度量單位并得到 N 個，那么物體的維度 D 滿足 N = n^D.（所以直線有 n1 個塊，正方形有 n2 個塊，立方體有 n3 個塊）。重新排列，我們得到 D = ln（N）/ln（n）。目前為止，一切都好。

現在讓我們來看看科赫曲線。你認為科赫曲線是一維的，這是可以原諒的——畢竟，我們之前使用的迭代結構的每一步都只是將直線放在一起。但這就是無窮大介入并動搖我們的直覺的地方：當我們將這個過程迭代到無窮小時，實際上沒有任何“直線碎片”留在任何地方。相反，回想一下，在構造的每一步中，我們取了 4 個大小為 1/3 的碎片，并重復此操作到無窮小。因此，科赫曲線的分形維數為 D = ln（4）/ln（3） ≈1.262——這不是一個整數！這表明科赫分形在某種程度上不僅僅是一條線，它的無限性有點“推出”到多個維度。

同樣，當我們構建謝爾賓斯基三角形時，我們使用了 3 條線的副本，這些線的大小是 1/2。因此，對于謝爾賓斯基三角形，我們有 D = ln（3）/ln（2） ≈1.585。這個數字比科赫曲線大，我們可以直觀地看到這種差異——謝爾賓斯基三角形比科赫曲線填充了更多的空間。

五、希爾伯特曲線

現在讓我向你展示另一種類型的分形曲線，稱為希爾伯特曲線，它是由數學家大衛希爾伯特在1891年發現的。其構建的前幾個步驟如下所示：

你可能會注意到，這條曲線似乎以這樣一種方式蜿蜒曲折，填滿了大量的空間——甚至比謝爾賓斯基三角形還要多，后者有明顯的孔洞區域。

那么，希爾伯特曲線的分形維數是多少？

在每個步驟中，我們都使用 4 個大小為 1/2 的部件（以及一點額外的線來連接這些部件）。因此，我們有 D = ln（4）/ln（2） = 2。也就是說，當被拿到無窮小時，希爾伯特曲線實際上是二維的，盡管它是由直線碎片構成的！事實上，當分形被取到無窮小時，它與實心正方形是無法區分的，像這樣的曲線被稱為空間填充曲線。

我們的朋友龍曲線也是一條空間填充曲線，盡管它填充空間的方式不如希爾伯特曲線的整齊正方形那么直接。再一次，我們可以通過查看 Dragon 曲線的分形維數來看到這一點。在每個步驟中，我們使用 2 個大小為 1/√2 的碎片（或者，每第二步使用 4 個大小為 1/2 的碎片），因此我們得到 D = ln（2）/ln（√2） = 2。
?
為什么你認為分形如此重要？
我不認為它們本身是“重要的”，但有許多自然發生的結構具有類似分形的性質。當然，當你達到原子尺度時，物理世界中的任何事物的細節都會受到限制（這是一件有趣的事情，向你展示了我的意思）。因此，它們只是真正的數學分形的近似值。

其中最明顯的是雪花，它們具有分形狀的晶體結構。

雷擊是另一種自然現象，當閃電從云層中展開，尋找與地面的最佳接觸點時，它通常表現出分形性質。這是我看過的最好的慢動作視頻之一，它展示了閃電分形的美感。

還有營養豐富的分形！Romanesco 西蘭花是可食用（和健康）分形的一個很好的例子。

亞當在左邊畫了分形西蘭花，所以我們認為找到谷歌的版本可能也會有所幫助！

六、還有什么有趣的要補充的嗎？

是的，實際上。

之前我談到了一種生成自相似分形的迭代方法。您可能還記得，我們通過從一條直線開始，將上一次迭代的兩個副本彼此成直角放置來構建 Dragon 曲線。事實證明，如果您反復將一張紙對折（沿同一方向折疊），然后展開它，使每次折疊都是直角，這正是您得到的！

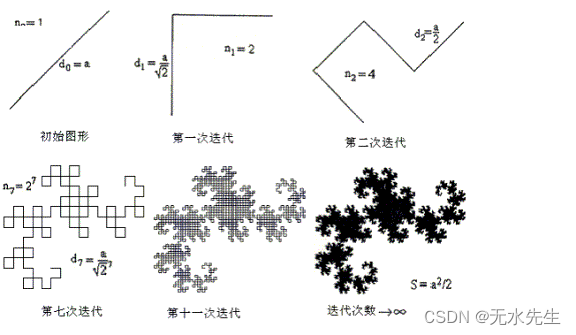
這看起來似乎就是一點點構圖，畫出它們，我們已經搞得一團糟。到處都是鋼筆、餐具和紙屑！然而渲染一種自然景觀，比如下圖：

這就成了電腦構圖的另一層境界，總之，分型幾何是一個優質資源。