一：revise

我們在最開始提出一個線性模型。

x為我們的輸入，w為權重。相乘的結果是我們對y的預測值。

那我們在訓練時就是對這個權重w進行更新，就需要用到上一章提到的梯度下降算法，不斷更新w。但是此時注意不是用y的預測值對w進行求導，應該是使用loss損失值對w權重進行求導，因為我們需要得到最小的loss。

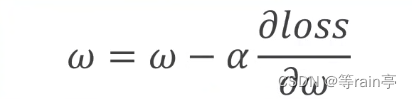
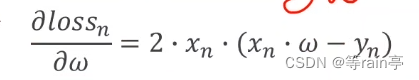
對于簡單的模型我們可以使用解析式去解決，但是對于復雜的模型的w會很難算。

最左邊的5個?代表的是5個輸入，右邊的5個?代表的是5個輸出，中間的每個?都是隱藏的值設為H。中間的4列我們如果用向量表示，分別都是一個六維的向量，而我們想用輸入的五維向量得到六維向量，就需要使用輸入的五維向量乘上6x5的矩陣才能得到這個六維的向量，這就意味著我們需要30個不同的w，其實也就對應著我們圖片上的線，每條線都代表需要一個w。

所以此時如果要是寫解析式就是一件非常復雜的事情，因此我們希望做一種算法把我們的網絡看成一個圖，在圖上進行傳播，根據鏈式法則把梯度求出來。這個就是我們想要完成的bp（back propagation）

二：forward

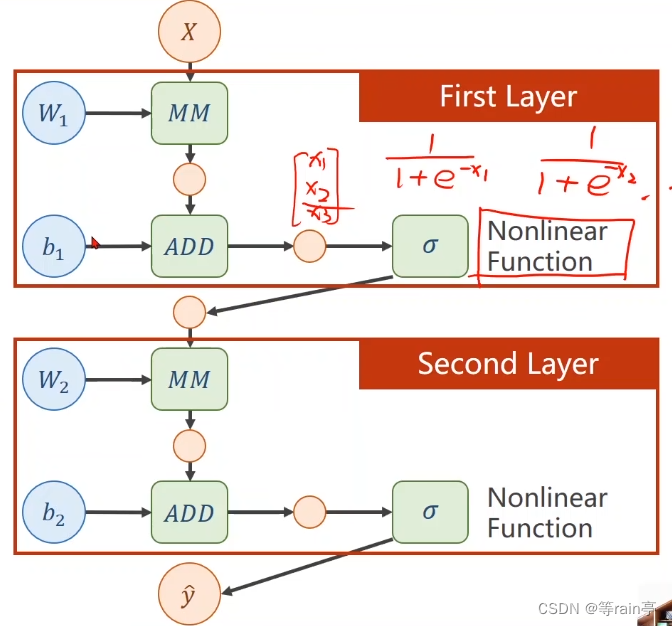
先來一個簡單的兩層神經網絡：

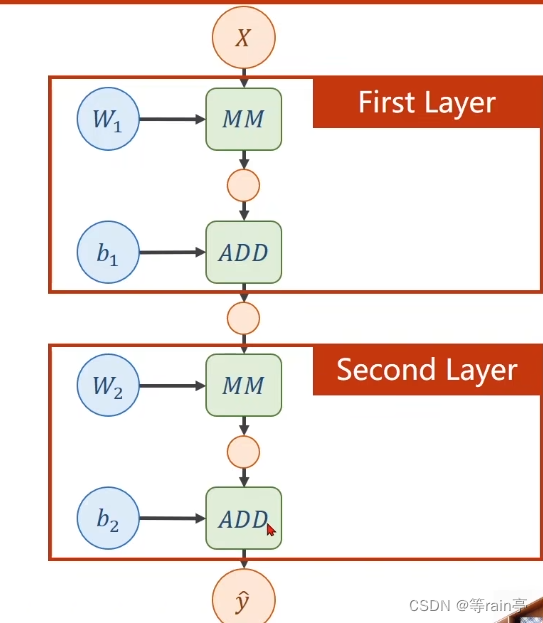
我們現在一層一層分析，其實可以看出兩層的操作都是一樣的。首先第一層計算的是w1*x+b1，假如說我們的輸入x是一個n維的列向量，結果是一個m維的列向量，MM是矩陣相乘，那我們需要的w1是一個m*n的矩陣，相乘得到的結果是一個m維的列向量，需要b1也是一個m維的列向量，ADD表示相加，得到的結果可以看成這個層的輸出，但其實這個值還需要放入到下一層進行第二層的運算，而兩個的運算過程都差不多，大家可以自己看一下。

ok，現在知道每一層的運算了，但是有一個問題出現了。

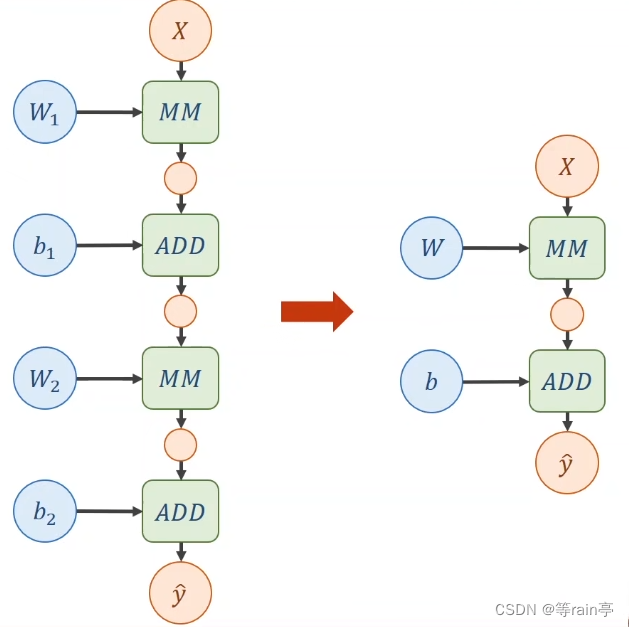
大家看，在一個線性的運算中，其中不管有多少層，w1，w2都是可以通過計算放在一起的，那最后得到的結果也可以看出來，又是一個新的線性運算。這樣就意味著，無論我們經過多少層的運算，最后得到的還是一個線性的運算。

為什么說這樣不行，因為我們不希望化簡，這樣會導致我們的那些增加的權重沒有意義，所以我們需要對每一層最終的輸出加上一個非線性的變化函數。如下圖所示：

三：BP

3.1 鏈式法則

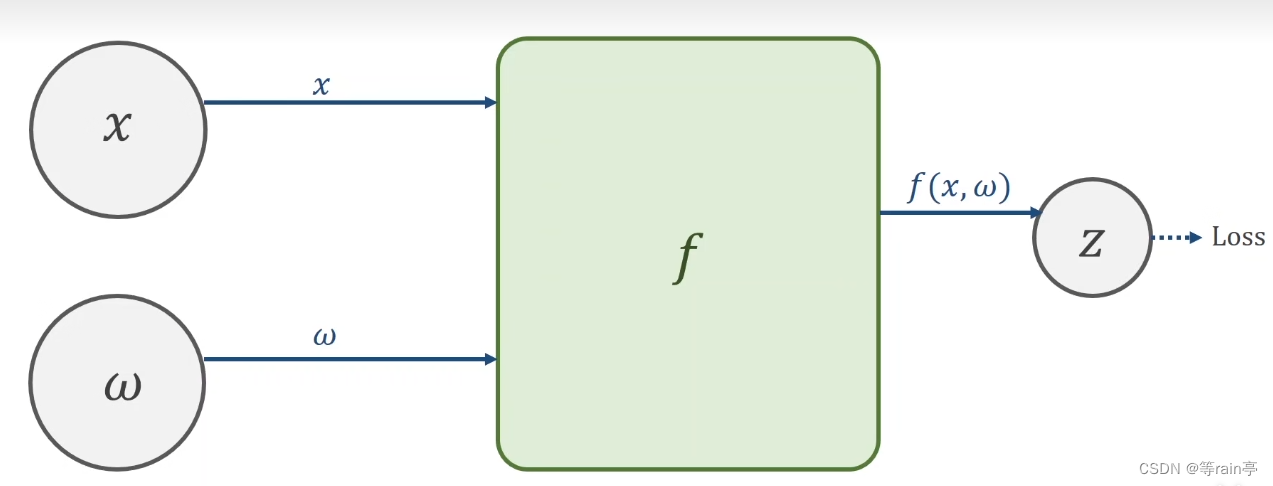
鏈式求導第一步就是需要創建計算圖。

接下來就是一個前饋forword，其實就是先有x，w通過f函數計算出z，最后得到loss的值。

現在我們如果想知道loss對于x或者w進行求導數，就是需要我們的鏈式法則，這個過程也就是bp（back propagation）。過程就是如下圖

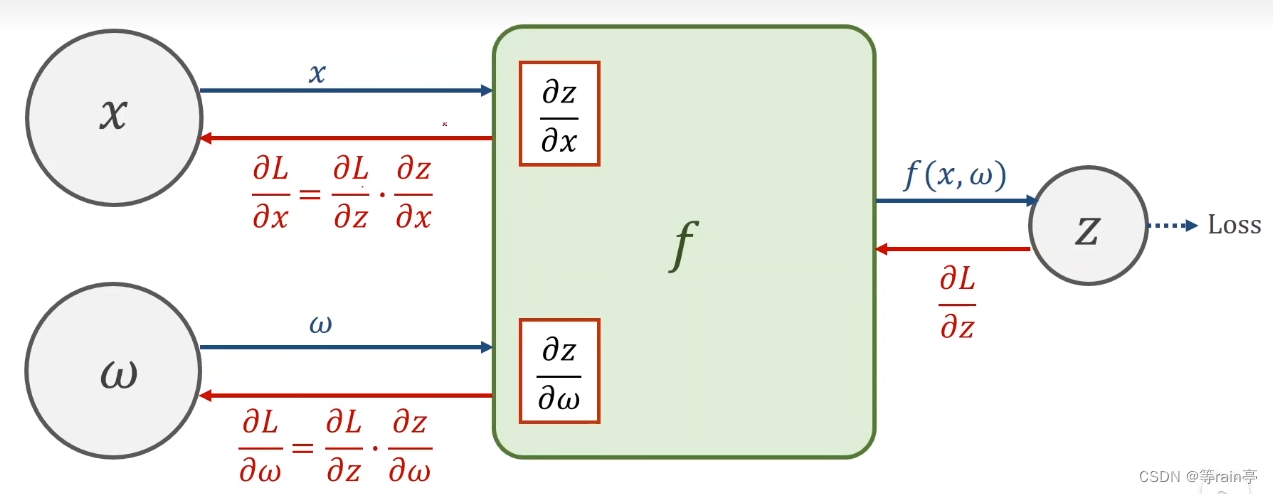
?ok，現在舉一個具體的例子1：設x=2，w=3，f(x,w)=x*w。求z的值和求z對w和x求導的結果。大家可以自己計算一下，結果看文末。

3.2整體流程

現在大家目光向下：整體的過一遍流程，先前饋forward，后backward。

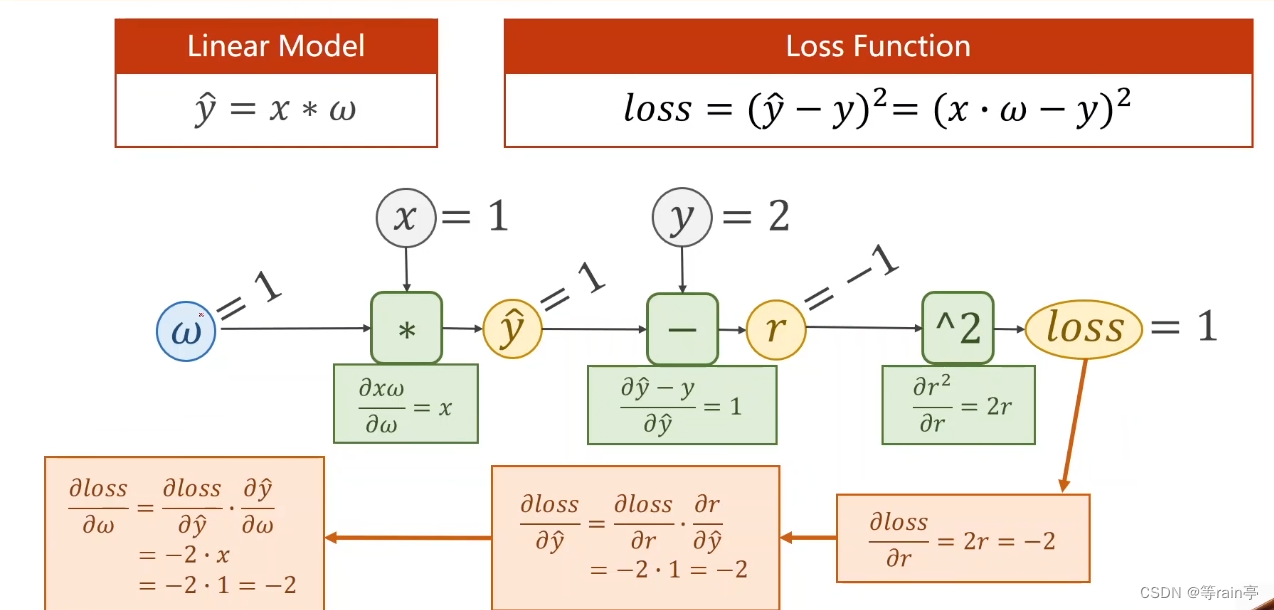
這個例子中給出的y_head的計算公式，就類似于我們上面提到的f（x，w）函數，和loss的計算公式。給出了w=1，x=1，y=2，其中r為y_head 減去y。首先計算出y_head為1，隨后計算出r為-1，最后算出loss為1，以上為forward過程。接下來就是backforward，通過鏈式法則的知識，先通過loss和r的函數關系，用loss對r進行求導，接著r對y_head求導，最后y_head對w求導，幾個結果相乘最終得到的就是loss對w求導的結果。

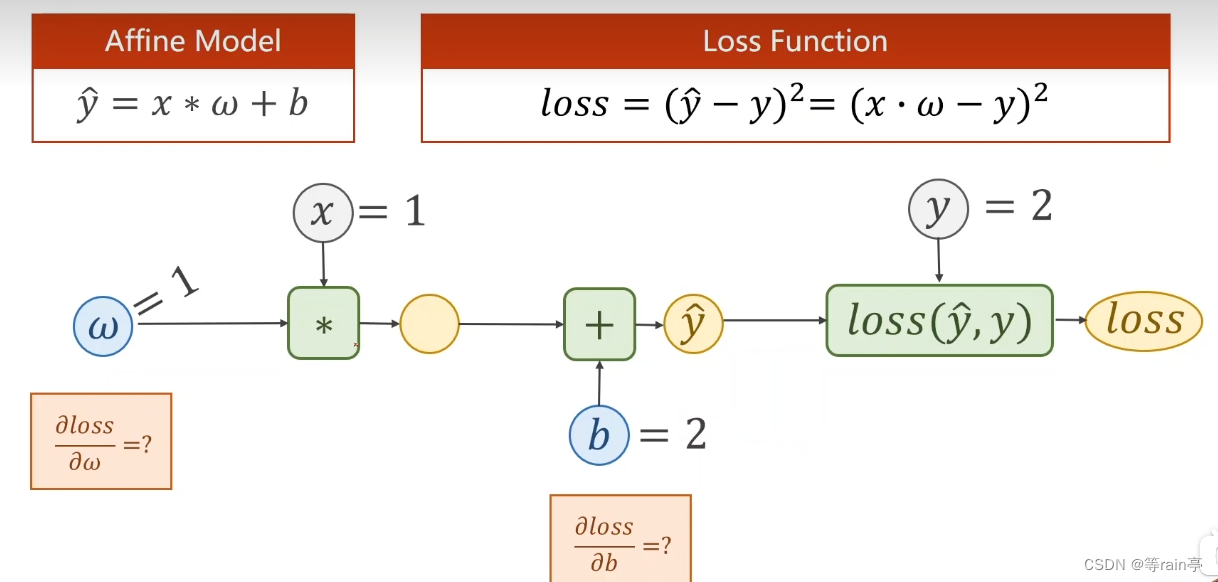
上面的計算大家也學會了，現在加上一個偏置量，大家計算一下loss值，loss對b和w的導數。此為例2，結果在文末。

3.3 tensor

在pytorch里最重要的數據成員就是tensor，存我們上面提到的一些數值，數據可以是標量，矩陣或者高階的tensor，其中有兩個比較重要的成員，一個是data（用于存放w本身的值），一個是grad（用于存放loss對于w的梯度值）。在鏈式法則部分我們提到，鏈式求導第一步就是需要創建計算圖，這個就是使用tensor創建的。

第一部分代碼，輸入的相關參數：

import torch#為舉例子，自己設置的值
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]w = torch.tensor([1.0])
w.requires_grad = True  #默認是不進行梯度計算的，我們讓他為true就是進行梯度計算

第二部分代碼，確定計算的一些步驟：

def forward(x):return x * wdef loss(x,y):y_pred = forward(x)return (y_pred - y)**2

?此時有一個需要注意的點，我們在第一步的時候設置的w是一個tensor值，當它遇到*時間，，此時的*已經被重載了，現在進行的是tensor于tensor的數乘。但是此時x并不是一個tensor類型，會自動轉化為tensor。此時就構建出類似于這樣的計算圖

?并且由于我們最后需要對w計算梯度，所以求出的z也需要計算梯度。

同理定義的loss函數也會建立出一個計算圖。

第三步就是計算過程。

print('predict (before training)',4,forward(4).item())for epoch in range(100):for x,y in zip (x_data,y_data):l = loss(x,y) #這一步是前饋的過程l.backward() #這一步是bp的過程，注意bp完會消除所有的計算圖print('\tgrad:',x,y,w.grad.item())w.data = w.data - 0.01 *w.grad.data #此時注意一定要.data 因為w是一個tensor，而我們需要的是tensor里面的dataw.grad.data.zero_() #在上一步的更新完，導數還存在，所以我們需要將其清零。print('progress',epoch,l.item())print('predict(after training)',4,forward(4).item)

現在大家應該知道整體的流程和代碼了，現在大家可以自己嘗試去寫一下下面這個流程。關于x_data于y_data的值與上面的值相同，大家可以嘗試一下。

四：answer

例子1：z的結果為6，z對w和x求導的結果分別為10和15。

例子2：z的結果是1，z對w和x求導結果分別為2和2。