二叉樹的鏈式結構（二叉樹）與順序結構（堆）---數據結構

一、樹的概念與結構

1、樹的概念

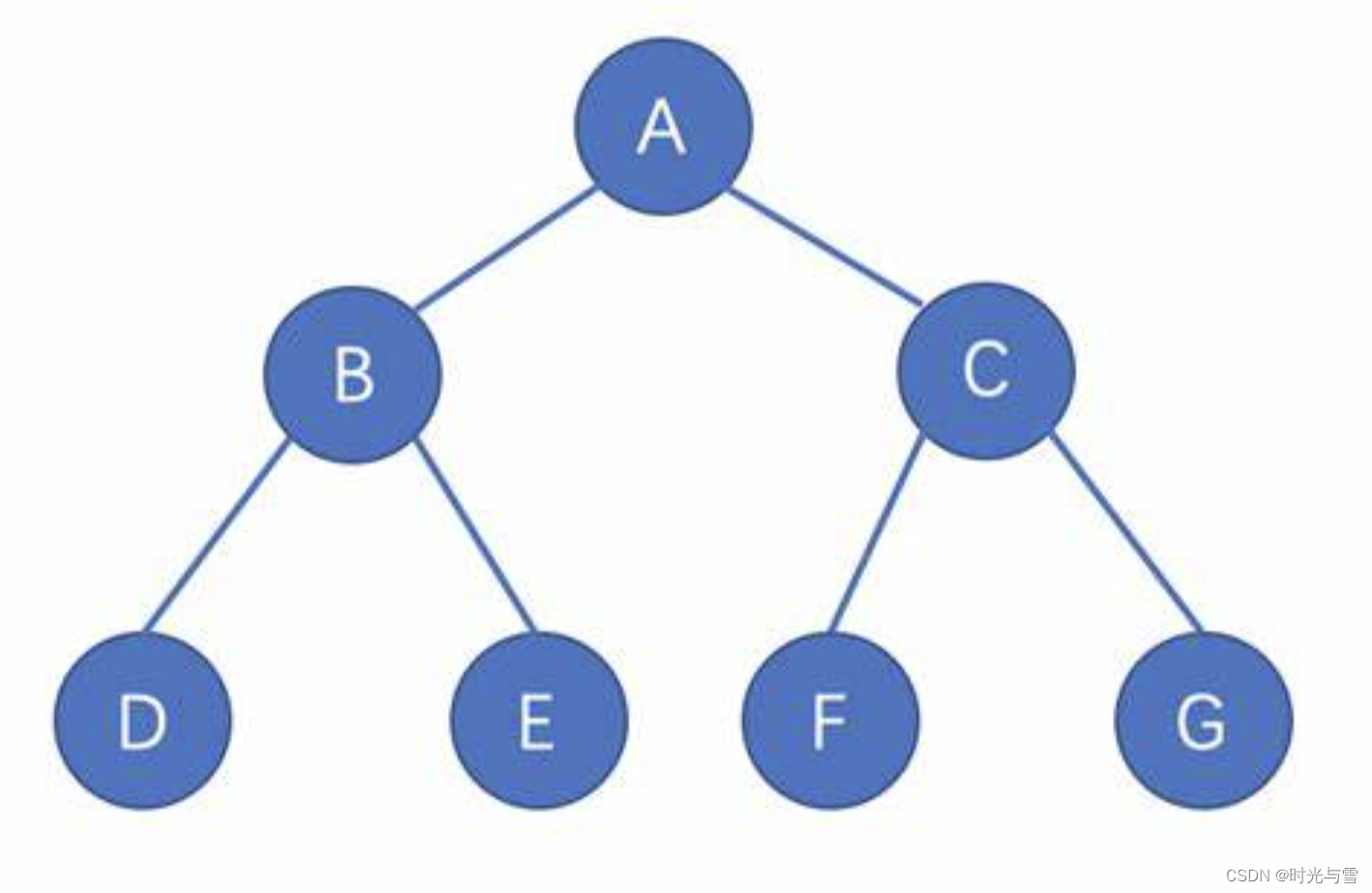
????????樹是一種非線性的數據結構，它是由n（n>=0）個有限結點組成一個具有層次關系的集合。我們常把它叫做樹，是因為它看起來像一棵倒掛的樹，它的根是朝上的，而葉是朝下的。

下面是樹的示意圖：

(1)->?在樹中有一個特殊的結點，稱為根結點，與樹的根類似，根結點以前不會再有前驅結點；
(2)-> 除根結點外，其余結點被分成M(M>0)個互不相交的集合T1、T2、……、Tm，其中每一個集合Ti(1<= i =<= m)又是一棵結構與樹類似的子樹。每棵子樹的根結點有且只有一個前驅，但可以有0個或多個后繼節點，因此，一棵樹可以看成：根節點+它的子樹。就例如上面的這棵樹，就可以看成根節點 ' A ' 與左右兩顆子樹 ' B ' 和 ' C ' 所構成；而 ' B ' 子樹又可以看做根節點 ' B ' 與左右子樹 ' D ' 與 ' E ' 所構成；' C ' 子樹同理。所以這種由大化小的問題可以轉換為遞歸問題，因此樹是由遞歸所定義的。

注意：在樹形結構中，子樹之間不能有交集，否則就不是樹形結構！！！

例如下面的這幾棵樹就不是樹形結構：

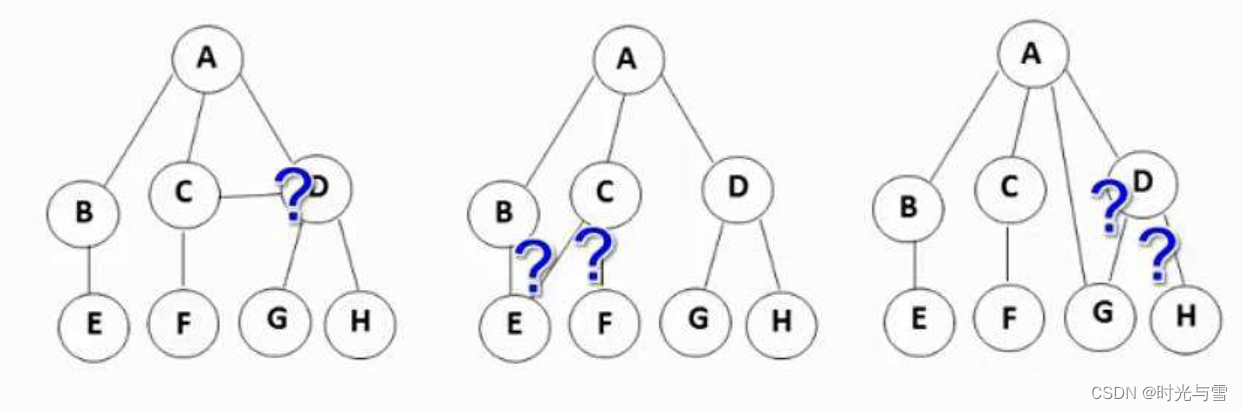
總結：

①子樹與子樹之間不可相交；

②一個有N個節點的樹有N-1條邊（每個父節點與子節點之間都由一條邊所連接）；

③除根節點以為的所有節點，有且只有一個父節點。

2、樹的相關概念

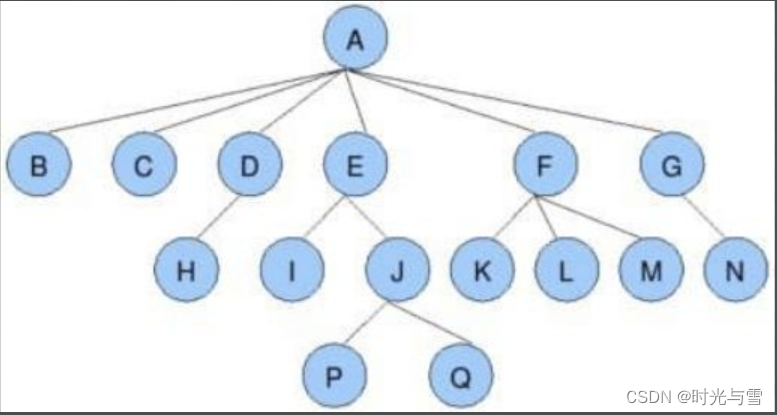
1->結點的度：一個結點所含的子樹的個數稱為該結點的度；如上圖：A的有6顆子樹，故A的度為6。
2->葉結點或終端結點：度為0的結點稱為葉結點；如上圖：B、C、H、I、P、Q、....等結點都為葉結點。
3->非終端結點或分支結點：度不為0的結點；如上圖：A、D、E、F、G...等結點為分支結點。
4->雙親結點或父結點：若一個結點含有子結點，則這個結點稱為其子結點的父結點；如上圖：A是B的父結點。

5->孩子結點或子結點：一個結點所含有的子樹的根結點稱為該結點的子結點；如上圖：B是A的孩子結點。
6->兄弟結點：具有相同父結點的結點互稱為兄弟結點；如上圖：B、C是兄弟結點。
7->樹的度：一棵樹中，最大的結點的度稱為樹的度；如上圖：樹的度為6（A結點的度）。
8->結點的層次：從根開始定義起，根為第1層，根的子結點為第2層，以此類推。
9->樹的高度或深度：樹中結點的最大層次；如上圖：樹的高度為4。
10->堂兄弟結點：雙親在同一層的結點互為堂兄弟；如上圖：H、I互為堂兄弟結點。
11->結點的祖先：從根到該結點所經過的分支上的所有結點；如上圖：A是所有結點的祖先。
12->子孫：以某結點為根的子樹中任一結點都稱為該結點的子孫。如上圖：所有結點都是A的子孫。
13->森林：由m（m>0）棵互不相交的樹的集合稱為森林。

3、樹的表示方法

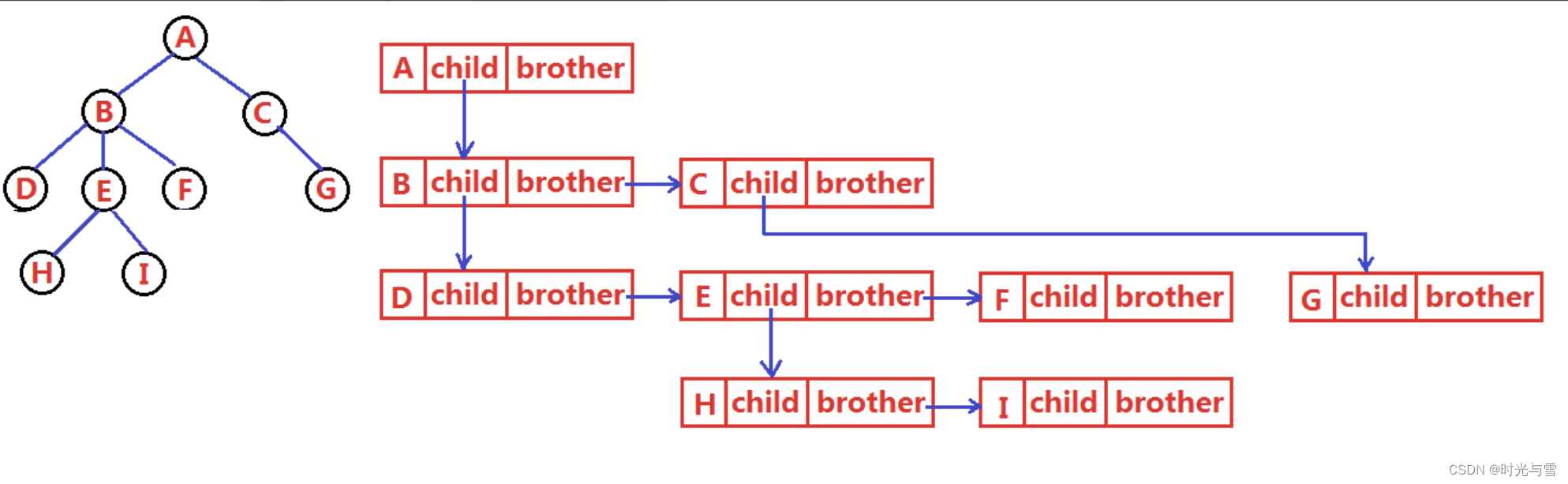
????????樹結構如果用線性表來表示的話就比較復雜了，要存儲表示起來就比較麻煩了，既然保存值域，也要保存結點和結點之間的關系，在實際中樹有很多種表示方式，例如：雙親表示法，孩子表示法、孩子雙親表示法以及孩子兄弟表示法等。我們這里就簡單的了解其中最常用的孩子兄弟表示法。?

typedef int DataType;
struct Node
{struct Node* firstChild1;  // 第一個孩子結點（最左邊的孩子節點）struct Node* pNextBrother; // 指向其下一個兄弟結點DataType data;             // 結點中的數據域
};

4 樹在實際中的運用

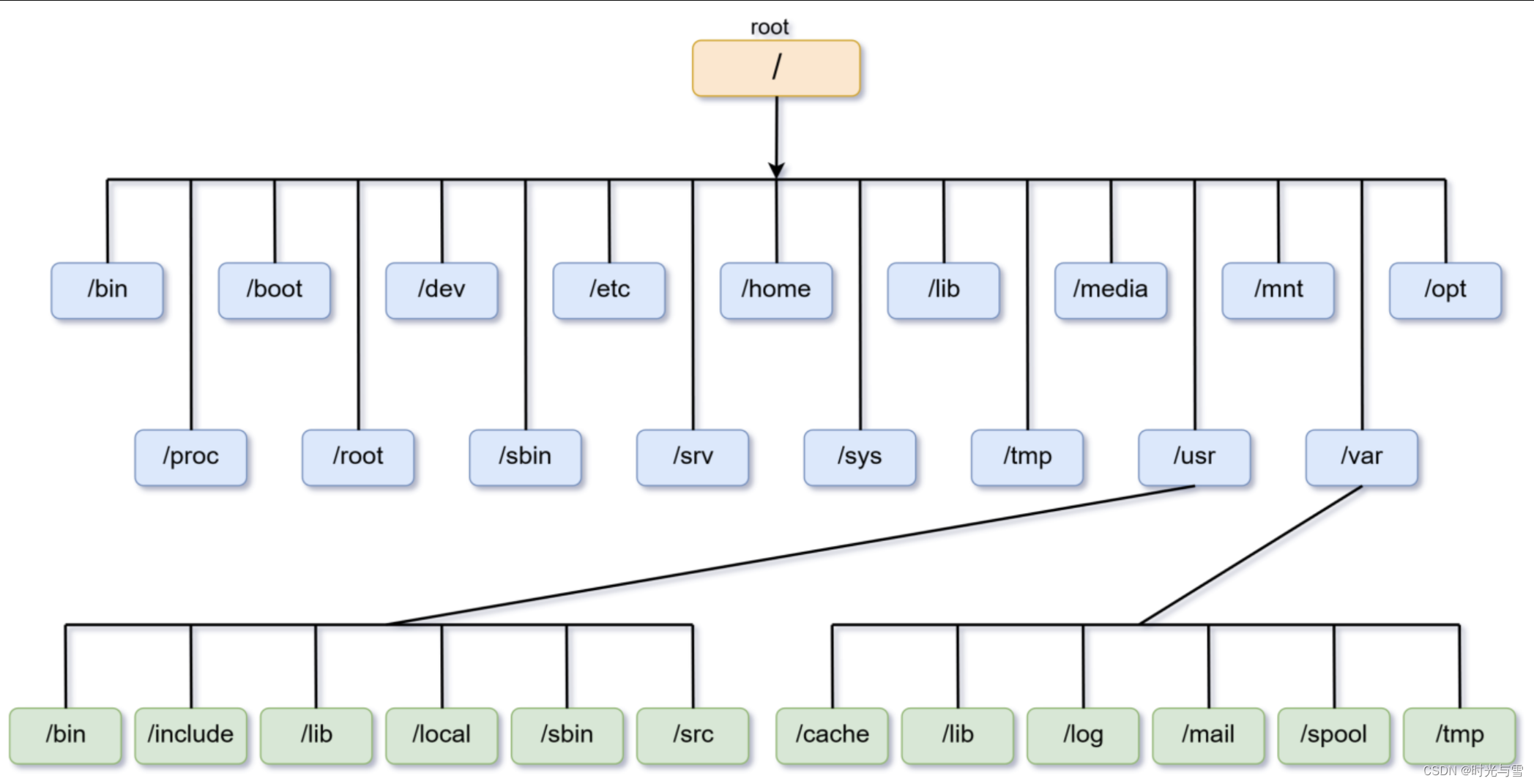
? ? ? ? 樹在實際中的應用十分廣泛，我們現在所使用的手機與電腦都離不開樹的功勞，例如Linux中的樹狀目錄結構：

二、二叉樹概念及結構?

1、二叉樹的概念

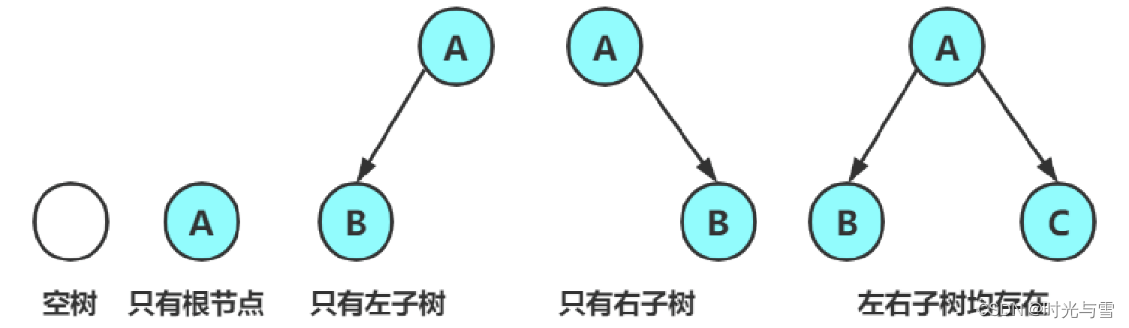
? ? ? ? 一顆二叉樹是節點的有限集合，若集合為空，表明沒有節點；若不為空，則該二叉樹由根結點與左子樹和右子樹組成，當然，這里的左子樹與右子樹也有可能為空。

二叉樹的特點：

1->二叉樹不存在度大于2的結點。
2->二叉樹的子樹有左右之分，次序不能顛倒，因此二叉樹是有序樹。

注意：所有的二叉樹結構都是由下面幾種情況所復合形成的：
?

2、特殊的二叉樹?

1-> 滿二叉樹：一個二叉樹，如果每一個層的結點數都達到最大值，則這個二叉樹就是滿二叉樹。

滿二叉樹示意圖：

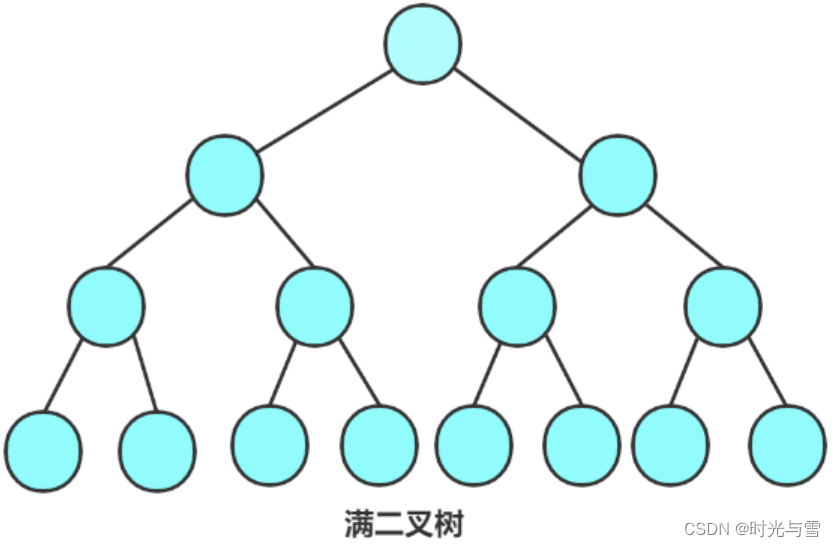
2-> 完全二叉樹：完全二叉樹是一種效率很高的數據結構，完全二叉樹是由滿二叉樹而引出來的。對于深度為K的，有n個結點的二叉樹，當且僅當其每一個結點都與深度為K的滿二叉樹中編號從1至n的結點一一對應時稱之為完全二叉樹，通俗來說，也就是前 K-1 層都與滿二叉樹中的 K-1層相同，第K層的節點必須是從左向右依次存放?。要注意的是滿二叉樹是一種特殊的完全二叉樹。

完全二叉樹示意圖：

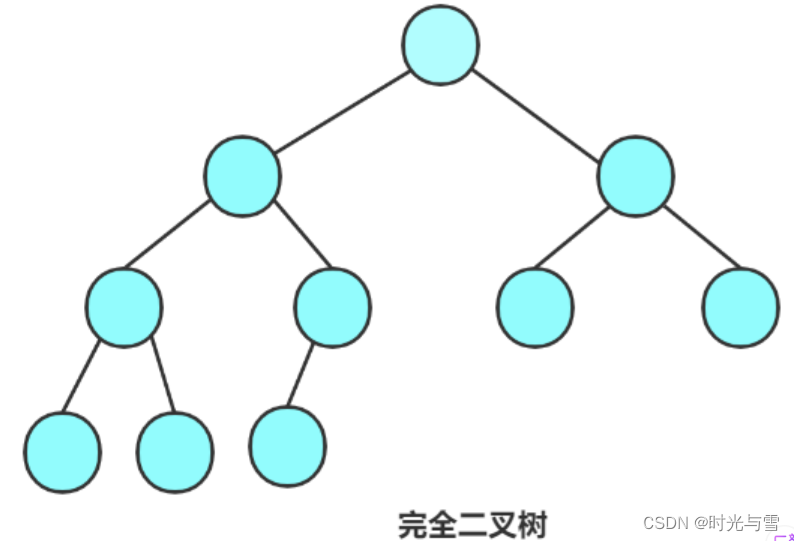
3、二叉樹的性質

1. 若規定根結點的層數為1，則一棵非空二叉樹的第i層上最多有 $2^{i-1}$ 個結點。

第1層最多有? $2^{0}$ ?個結點，第2層最多有? $2^{1}$ ?個結點，......第 i 層最多有? $2^{i-1}$ ?個結點，以此類推。

2. 若規定根結點的層數為1，則深度為h的二叉樹的最大結點數是 :? $2^{h}-1$ ?(深度為h的滿二叉樹的節點數)。

3. 對任何一棵二叉樹, 如果度為0其葉結點個數為 $n_{_{0}}$ , 度為2的分支結點個數為? $n_{_{2}}$ ,則有 $n_{_{0}}$ ＝ $n_{_{2}}$ ＋1。

證明：

設?n0 、?n1 、?n2 分別為?度為0、度為1、度為2 的節點個數。

?總結點數N：N = n0 + n1 + n2 ①
?
?N個結點的任意二叉樹，總共有N-1條邊：
* 因為二叉樹中每個結點都有雙親，根結點沒有雙親，每個節點向上與其雙親之間存在一條邊
* 因此N個結點的二叉樹總共有N-1條邊。

* 因為度為0的結點沒有孩子，故度為0的結點不產生邊; 度為1的結點只有一個孩子，故每個度為1的結點產生一條邊; 度為2的結點有2個孩子，故每個度為2的結點產生兩條邊，所以總邊數為：
? N-1 = n1 + 2*n2 ②
* 結合① 和 ②得：n0 + n1 + n2 -1 = n1 + 2*n2
* 即：n0 = n2 + 1
?

4. 若規定根結點的層數為1，具有n個結點的滿二叉樹的深度，h =? $\log (n+1)$ (ps： $\log (n+1)$
是log以2為底，n+1為對數)。
5. 對于具有n個結點的完全二叉樹，如果按照從上至下從左至右的數組順序對所有結點從0開始編號，例如：

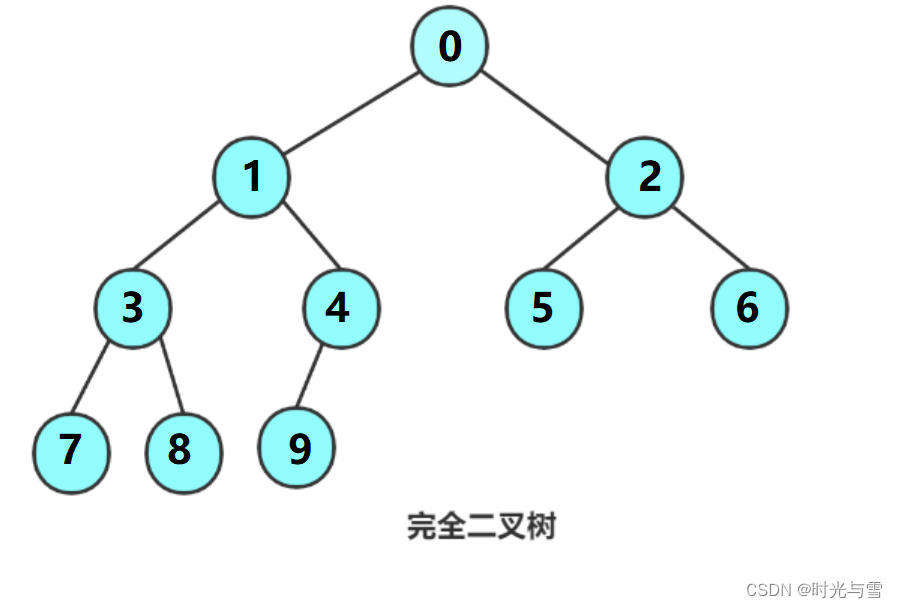
則對于序號為i的結點有：
1. 若i>0，i位置結點的雙親序號：(i-1)/2；i=0，i為根結點編號，無雙親結點
2. 若2i+1<n，左孩子序號：2i+1；若2i+1>=n則無左孩子
3. 若2i+2<n，右孩子序號：2i+2；若2i+2>=n則無右孩子?

4、二叉樹的存儲結構

二叉樹一般使用兩種結構存儲，一種是順序結構，另一種是鏈式結構。

1、順序存儲
????????順序結構存儲就是使用數組來存儲，一般使用數組只適合表示完全二叉樹，因為不是完全二叉樹會有空間的浪費。在現實中使用中只有堆才會使用數組來存儲，二叉樹用順序存儲在物理意義上是一個數組，在邏輯意義還上是一顆二叉樹。

例如：

完全二叉樹（無空間浪費）：

非完全二叉樹（有空間浪費）：

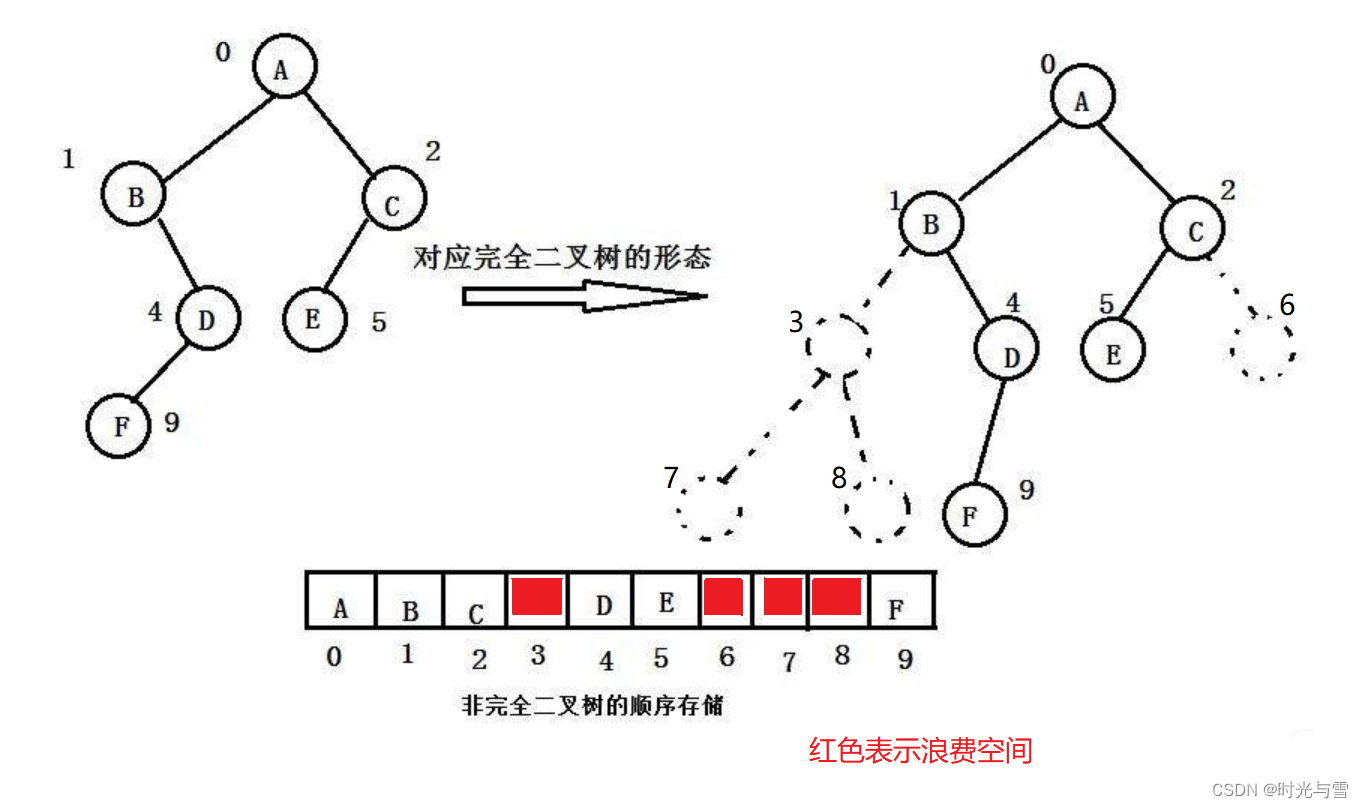
2、?鏈式存儲

????????二叉樹的鏈式存儲結構是用鏈表來表示一棵二叉樹，即用鏈來指示元素的邏輯關系。通常的方法中，鏈表的每個結點由三個域組成，數據域和左右指針域，左右指針用來找到出該結點的左孩子和右孩子所在的鏈結點的存儲地址。鏈式結構又分為二叉鏈和三叉鏈，當前我們學習中一般都采用的是二叉鏈，但高階的數據結構，如紅黑樹等會用到三叉鏈。?

下面我們分別快來看一下采用二叉鏈與三叉鏈的數據存儲結構：

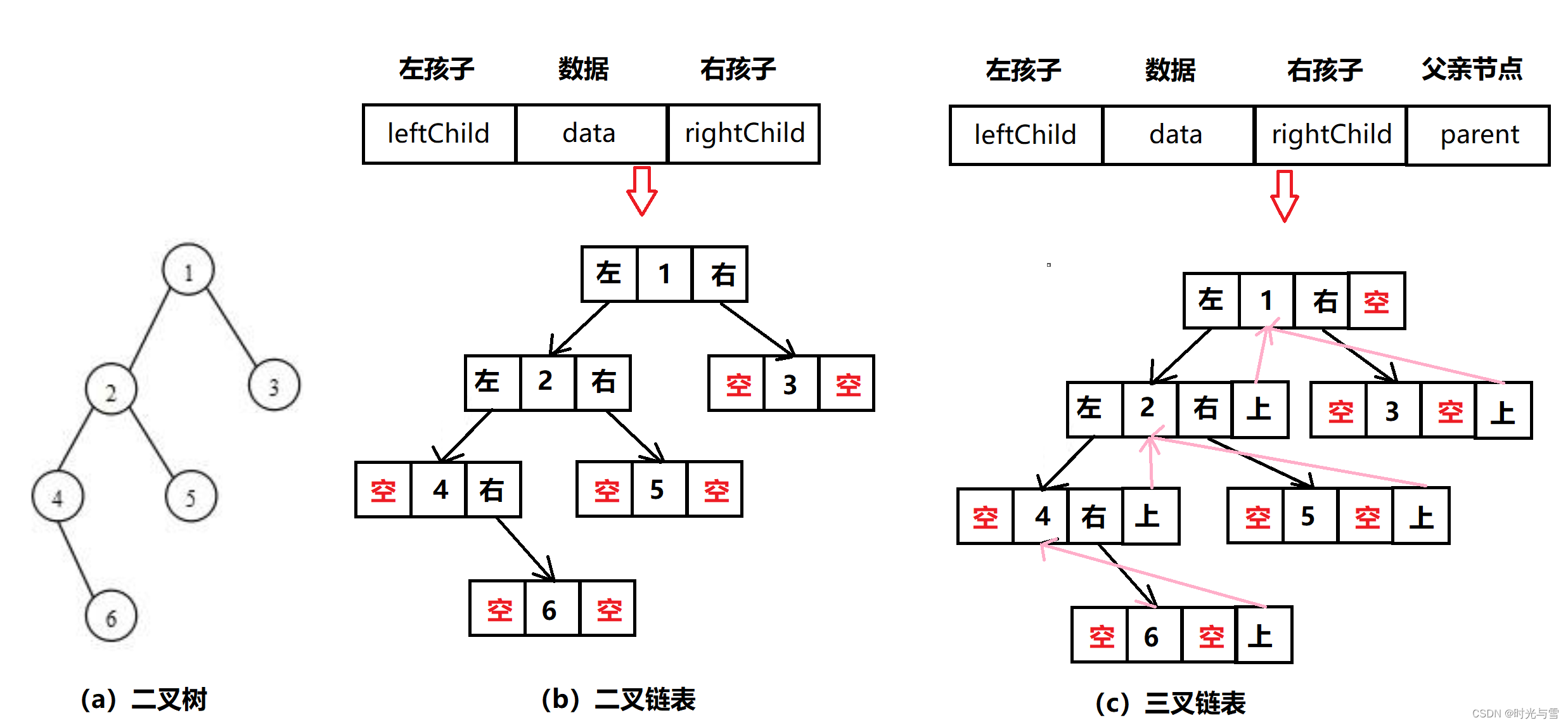
typedef int BTDataType;、// 二叉鏈
struct BinaryTreeNode
{struct BinTreeNode* left; // 指向當前結點左孩子 struct BinTreeNode* right; // 指向當前結點右孩子BTDataType data; // 當前結點值域
}// 三叉鏈
struct BinaryTreeNode
{struct BinTreeNode* left; // 指向當前結點左孩子struct BinTreeNode* right; // 指向當前結點右孩子struct BinTreeNode* parent; // 指向當前結點的雙親BTDataType data; // 當前結點值域
}；

三、二叉樹的順序結構及實現

1、二叉樹的順序結構

????????普通的二叉樹是不適合用數組來存儲的，因為可能會存在大量的空間浪費。而完全二叉樹更適合使用順序結構存儲。現實中我們通常把堆(一種完全二叉樹)使用順序結構的數組來存儲，需要注意的是這里的堆和操作系統虛擬進程地址空間中的堆是兩回事，一個是一種數據結構，一個是操作系統中管理內存的一塊區域分段。

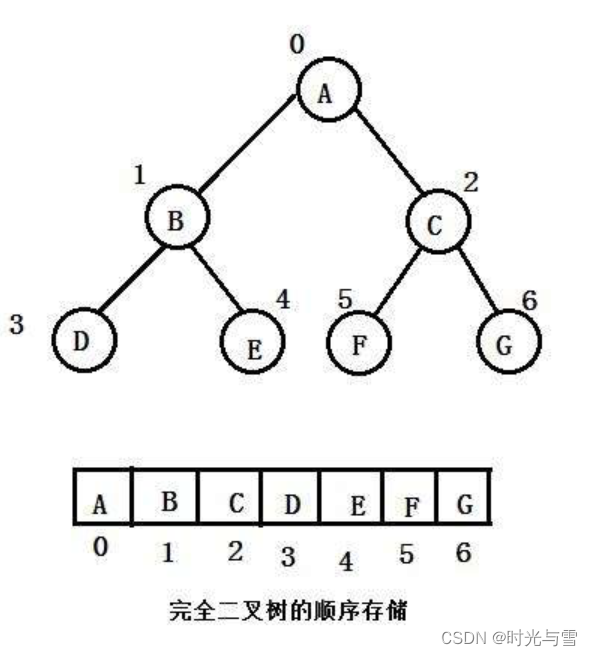
2、堆的概念及結構

????????如果有一個集合K = { K0，K1 ，K2 ，…，Kn-1?}，把它的所有元素按完全二叉樹的順序存儲方式存儲在一個一維數組中，并滿足： $K_{i}\leq K_{2i+1}$ 且 $K_{i}\leq K_{2i+2}$ （即孩子節點小于等于雙親節點）或者? $K_{i}\geq K_{2i+1}$ ?且? $K_{i}\geq K_{2i+2}$ ?（即孩子節點大于等于雙親節點），（i =0， 1，2…，）則稱為小堆(或大堆)。將根結點最大的堆叫做最大堆或大根堆，根結點最小的堆叫做最小堆或小根堆。

堆的性質：
? ? ? ?1->?堆中某個結點的值總是大于等于（孩子節點都大于等于父節點，即父節點更小，叫做小堆）或小于等于（孩子節點都小于等于父節點，即父節點更大，叫做大堆）其父結點的值；
? ? ? ?2-> 堆總是一棵完全二叉樹。?

小堆與大堆的示意圖：?

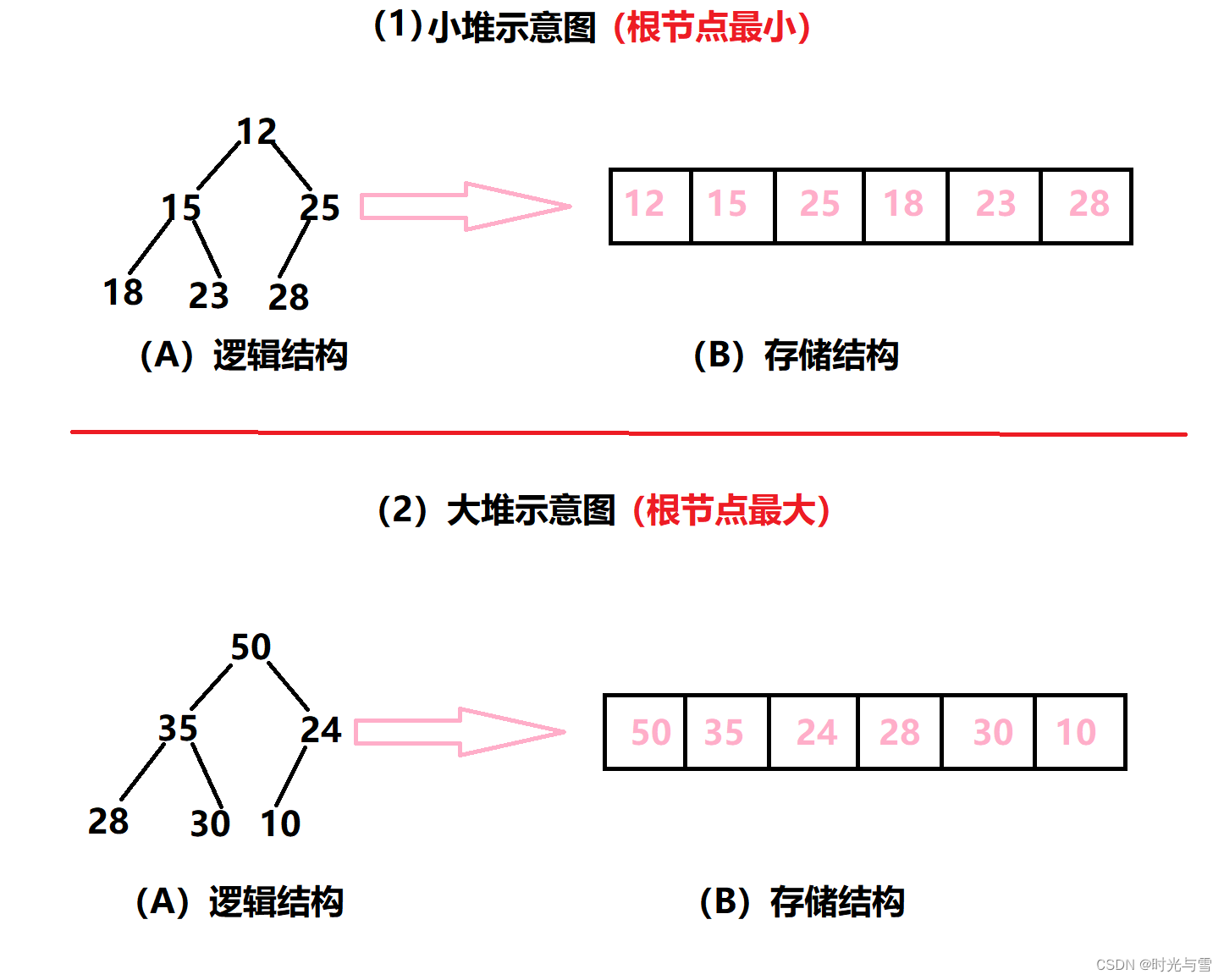
3、堆的實現?

1、堆的定義：


typedef int HPDataType;
typedef struct Heap
{HPDataType* _a;  // 數組int _size;       //元素個數int _capacity;   // 容量
}Heap;

2、堆的向上調整算法

? ? ? ? 首先我們先給出一個數組，在邏輯上將其看做一顆完全二叉樹。倘若我們現在的這個數組已經是一個堆（大堆或小堆），我們如果想往堆中插入一個元素，并使新堆依舊保持堆

的性質，那么我們對所插入的元素就需要進行向上調整算法。

int a[] = {15, 18, 19, 25, 28, 34, 65, 49, 27, 37};

下面我們以上面的小堆為例，對新插入的節點進行向上調整算法：

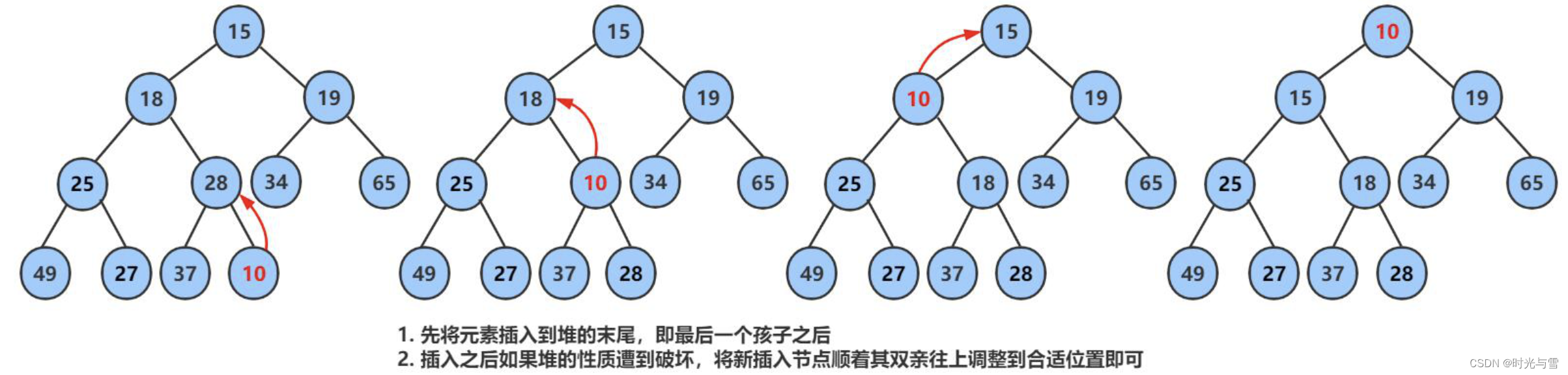
我們將新插入的元素放在二叉樹的最后一個節點的位置，并對其進行向上調整。

①我們首先先找到該節點的父節點，如果父節點的值更小，表明現在的新堆依然保持小堆的性質，不需要再進行調整；

②如果父節點的值更大，我們就需要交換新節點與父節點，并計算出下一個父節點的位置；

③如果下一個父節點還存在的話，就需要再次執行 ①② 步驟，直至沒有父節點或已經滿足小堆的性質。

示意圖：

代碼實現：

void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}
// HPDataType 是一種數據類型的重定義，這里是int 類型
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;   // 先找到新節點的父節點while (child > 0)     // child == 0 表明child已經是根節點了，不需要再進行調整{if (a[child] < a[parent])   // 孩子更小就與父節點交換{Swap(&a[child], &a[parent]);child = parent;           // 交換后的孩子節點來到了父節點的位置parent = (child - 1) / 2;   // 再找到下一個父節點}else    // 孩子節點的值更大就說明以滿足小堆的性質，不需要再交換{break;}}
}

3、堆的插入

? ? ? ? 通過上面的向上調整算法的學習，堆的插入也就變得十分的容易了，只需要將數據放在堆的最后，在對其進行向上調整即可。

代碼實現：


void HeapPush(Heap* hp, HPDataType x)
{assert(hp);if (hp->_capacity == hp->_size)   // 是否需要擴容{int NewCapacity = hp->_capacity == 0 ? 4 : 2 * hp->_capacity;HPDataType* New = (HPDataType*)realloc(hp->_a,sizeof(HPDataType) * NewCapacity);if (New == NULL){perror("HeapPush:malloc");exit(-1);}hp->_capacity = NewCapacity;hp->_a = New;}hp->_a[hp->_size] = x;   // 插入的數據放在最后 hp->_size++;AdjustUp(hp->_a, hp->_size-1); //將插入的元素向上調整
}

4、堆的向下調整算法

? ? ? ? 學習了向上調整算法后，我們再來看一下向下調整算法。首先我們先給出一個數組，在邏輯上將其看做一顆完全二叉樹。我們通過從根結點開始的向下調整算法可以把它調整成一個小堆，先找它的出孩子節點中較小的一個，在與其進行比較，若根節點的值大于較小孩子的值，就交換他們兩個的位置。一直循環此步驟，直至遇到他的孩子節點的值大于該節點的值或者沒有孩子節點就停止調整。

以下面這個數組為例：

int array[] = {27,15,19,18,28,34,65,49,25,37};

我們將其看做一個邏輯上的二叉樹：
?

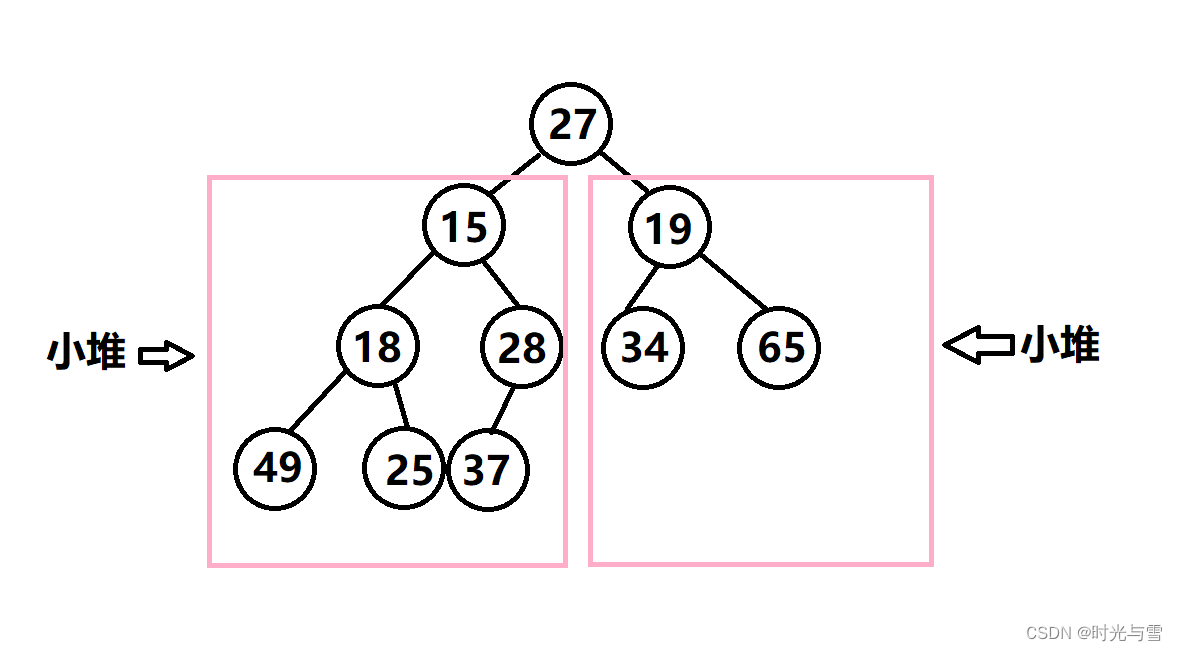
上樹的性質恰好滿足?向下調整算法，根節點的左右子樹都已經是一個小堆了，此時我們只需要向下調整根節點即可將整棵樹變成一個小堆，下面來看一下調整示意圖：

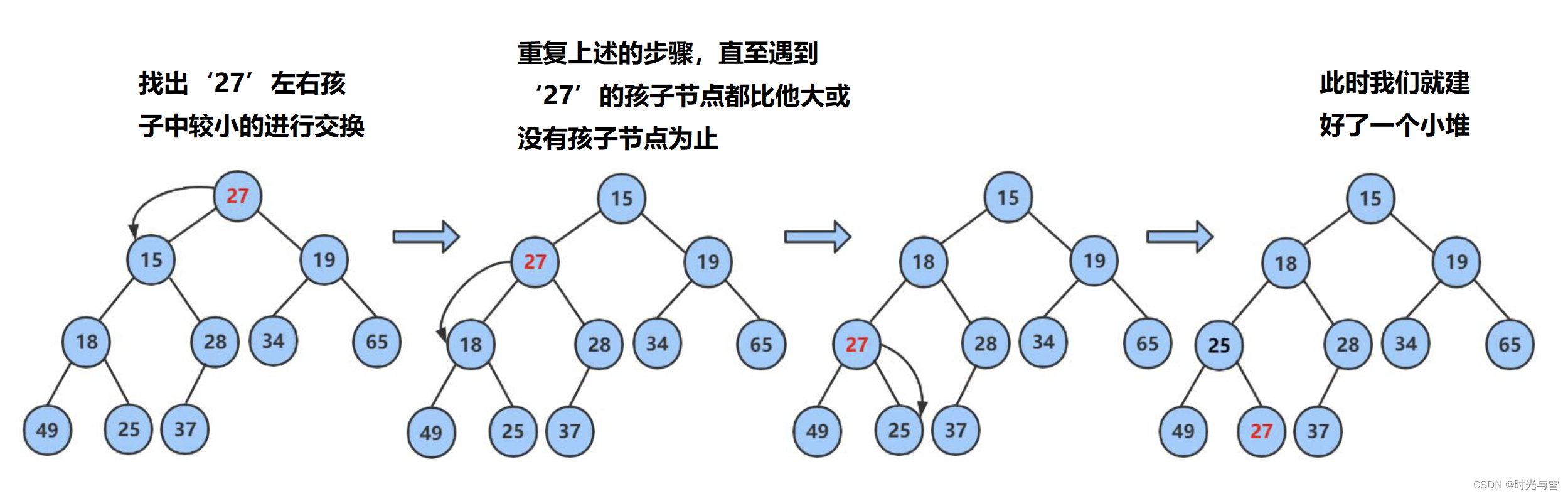
代碼實現：

void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}// HPDataType 是一種數據類型，這里是int類型
void AdjustDown(HPDataType* a, int size,int parent)
{int child = 2 * parent + 1;  // 左孩子while (child < size){// 存在右孩子    并且    右孩子更小if ((child + 1) < size && a[child + 1] < a[child])  // 找出左右孩子中較小一個{child++;}if (a[parent] > a[child])   // 如果孩子更小就交換，并且更新父節點與孩子節點{Swap(&a[parent], &a[child]);parent = child;child = 2 * parent + 1;} else     // 如果父節點更小表明不用再交換了 ，跳出循環{break;}}
}

5、堆的創建

????????通過上面我們學會了向下調整算法，但當根節點的左右子樹并不是一個堆時，我們又該如何進行調整呢？其實方法很簡單，既然左右子樹不是堆，我們就先調整左右子樹成為一個堆后，在對根節點進行調整；在調整左右子樹時，又可以單獨的將左右子樹看做一棵樹進行向下調整；如果左右子樹的子樹也不是堆的話，我們就需要先調整左右子樹的子樹。所以我們既可以得出一個結論：因為單獨的一個節點可以將其看做一個堆，所以對于葉子結點，我們不用對其進行向下調整；故我們從第一個非葉子節點開始進行向下調整。

int a[] = {1,5,3,8,7,6};

我們以上面的數組為例，對其進行向下調整使其成為一個大堆：

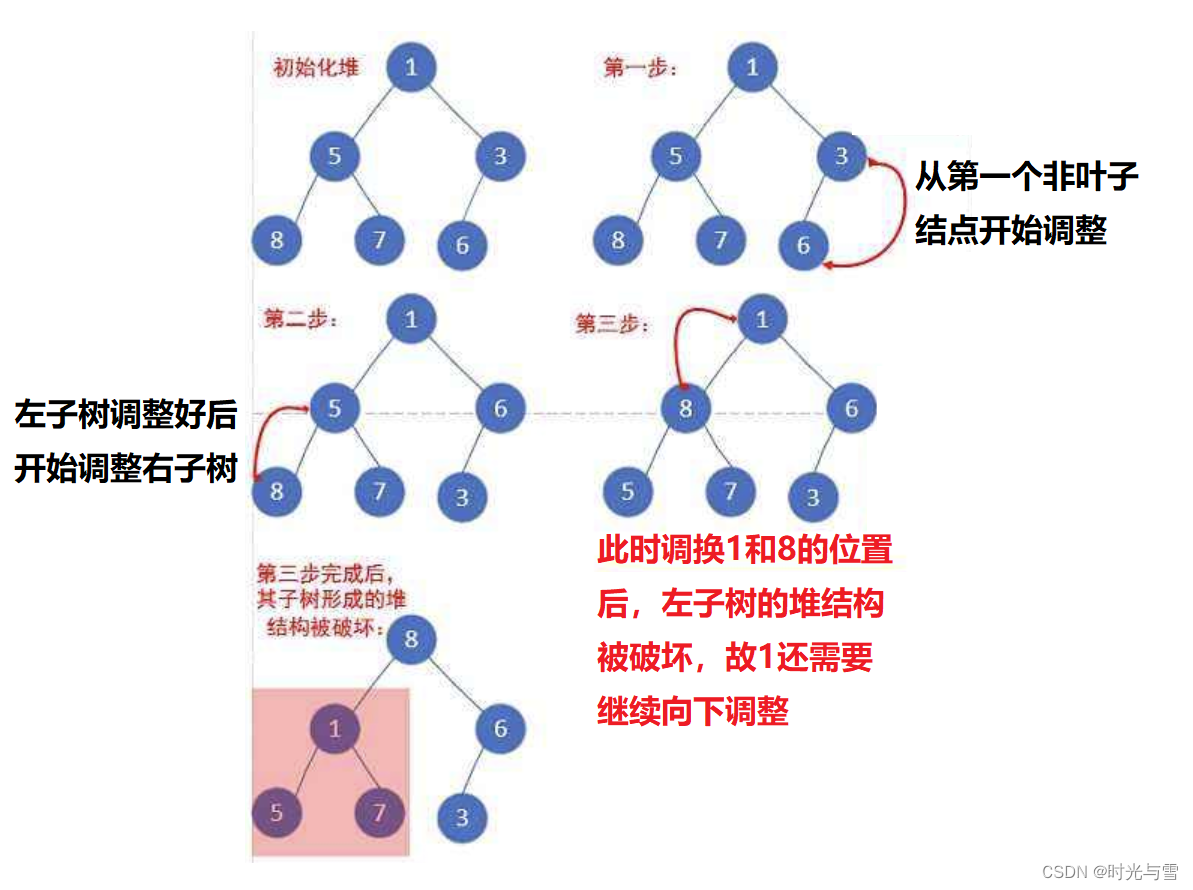
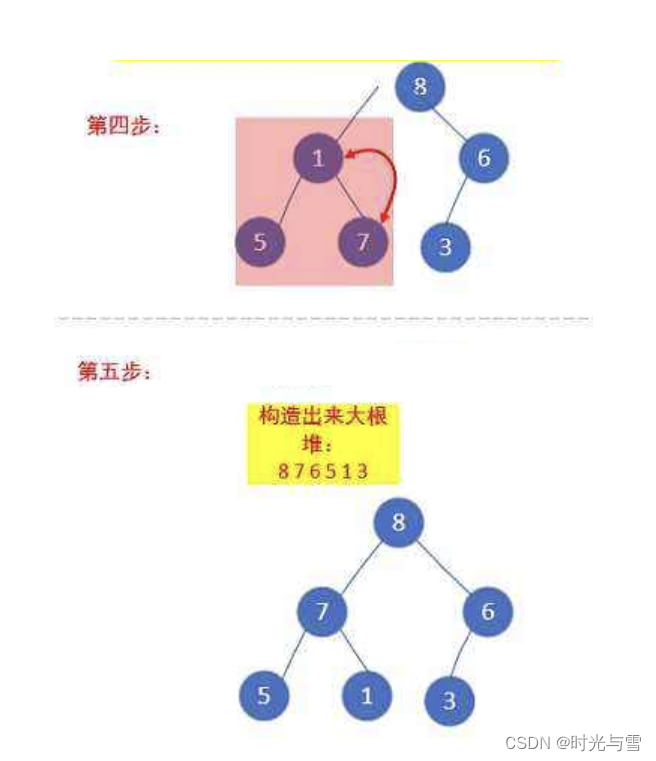
代碼實現：


void AdjustDown(HPDataType* a, int size,int parent)
{int child = 2 * parent + 1;while (child < size){if ((child + 1) < size && a[child + 1] > a[child])  // 找出左右孩子中較大一個{child++;}if (a[parent] < a[child])   // 如果孩子更大就交換，并且更新父節點與孩子節點{Swap(&a[parent], &a[child]);parent = child;child = 2 * parent + 1;} else     // 如果父節點更大表明不用再交換了 ，跳出循環{break;}}
}void HeapSort(int* a, int n)
{for (int i = (n - 1-1) / 2; i >= 0; i--)  // n-1 是最后一個節點，（n-1-1）/2就是第一個非葉子節點{AdjustDown(a, n,i);}
}

6、堆的刪除

????????堆的刪除是刪除堆頂的數據，先將堆頂的數據與最后一個數據交換，然后再刪除數組最后一個數據，但將最后一個數據交換到堆頂后，可能此刻的堆已經被打亂，所以還需要對堆頂的數據進行向下調整算法，使交換后的堆依舊滿足堆的性質。

int arr[] = {10, 15, 19, 25, 18, 34, 65, 49, 27, 37, 28};

我們以上面的堆為例，來看一下堆的刪除示意圖：

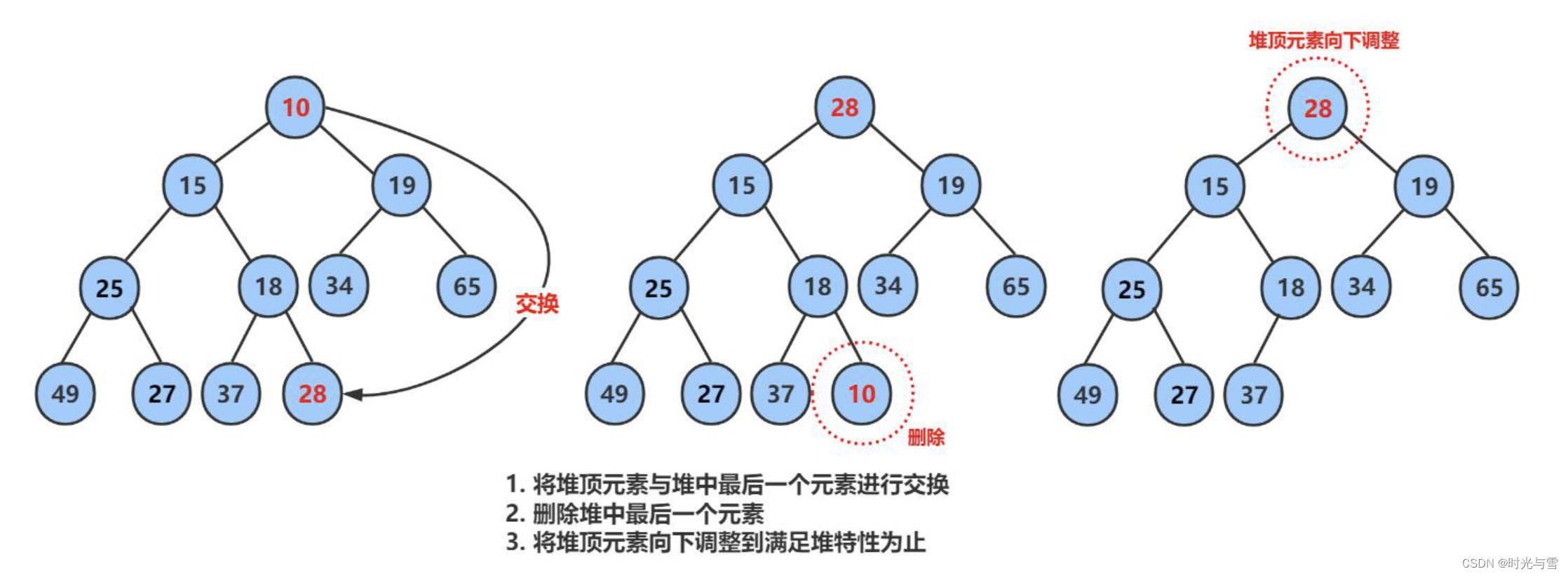
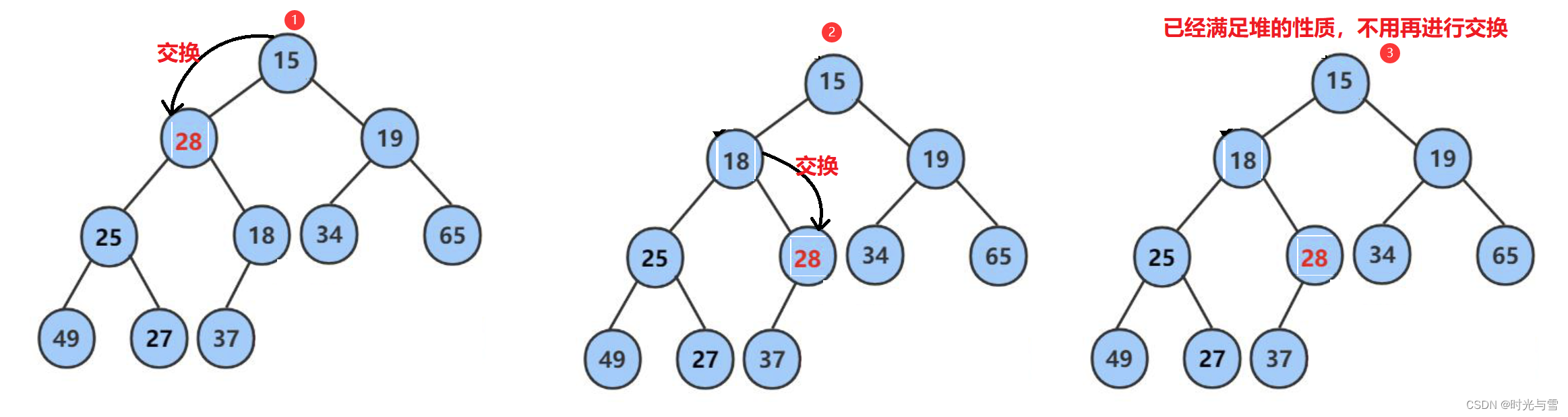
代碼實現：


void HeapPop(Heap* hp)
{assert(hp);assert(hp->_size);    // 確保有數據才能進行刪除hp->_a[0] = hp->_a[hp->_size - 1];   // 將最后一個元素放入堆頂hp->_size--; AdjustDown(hp->_a, 0, hp->_size);  //將堆頂的數據向下調整}

堆的全部代碼實現：

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>typedef int HPDataType;
typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap;// 堆的初始化
void HeapInit(Heap* hp);// 堆的銷毀
void HeapDestory(Heap* hp);// 交換兩個元素
void Swap(HPDataType* p1, HPDataType* p2);// 堆的插入
void HeapPush(Heap* hp, HPDataType x);// 向上調整
void AdjustUp(HPDataType* a, int child);// 堆的刪除 (刪除堆頂的數據)
void HeapPop(Heap* hp);// 向下調整
void AdjustDown(HPDataType* a, int size,int parent);// 取堆頂的數據
HPDataType HeapTop(Heap* hp);// 堆的數據個數
int HeapSize(Heap* hp);// 堆的判空
int HeapEmpty(Heap* hp);void HeapInit(Heap* hp)
{assert(hp);hp->_a = NULL;hp->_capacity = hp->_size = 0;
}void HeapDestory(Heap* hp)
{assert(hp);free(hp->_a);hp->_a = NULL;hp->_capacity = hp->_size = 0;
}void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}
// HPDataType 是一種數據類型的重定義，這里是int 類型
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;   // 先找到新節點的父節點while (child > 0)     // child == 0 表明child已經是根節點了，不需要再進行調整{if (a[child] < a[parent])   // 孩子更小就與父節點交換{Swap(&a[child], &a[parent]);child = parent;           // 交換后的孩子節點來到了父節點的位置parent = (child - 1) / 2;   // 再找到下一個父節點}else    // 孩子節點的值更大就說明以滿足小堆的性質，不需要再交換{break;}}
}void HeapPush(Heap* hp, HPDataType x)
{assert(hp);if (hp->_capacity == hp->_size)   // 是否需要擴容{int NewCapacity = hp->_capacity == 0 ? 4 : 2 * hp->_capacity;HPDataType* New = (HPDataType*)realloc(hp->_a,sizeof(HPDataType) * NewCapacity);if (New == NULL){perror("HeapPush:malloc");exit(-1);}hp->_capacity = NewCapacity;hp->_a = New;}hp->_a[hp->_size] = x;   // 插入的數據放在最后 hp->_size++;AdjustUp(hp->_a, hp->_size-1); //將插入的元素向上調整
}void AdjustDown(HPDataType* a, int size,int parent)
{int child = 2 * parent + 1;while (child < size){if ((child + 1) < size && a[child + 1] > a[child])  // 找出左右孩子中較大一個{child++;}if (a[parent] < a[child])   // 如果孩子更大就交換，并且更新父節點與孩子節點{Swap(&a[parent], &a[child]);parent = child;child = 2 * parent + 1;} else     // 如果父節點更大表明不用再交換了 ，跳出循環{break;}}
}void HeapPop(Heap* hp)
{assert(hp);assert(hp->_size);    // 確保有數據才能進行刪除hp->_a[0] = hp->_a[hp->_size - 1];   // 將最后一個元素放入堆頂hp->_size--; AdjustDown(hp->_a, 0, hp->_size);  //將堆頂的數據向下調整}// 取出棧頂的數據HPDataType HeapTop(Heap* hp)
{assert(hp);assert(hp->_size);return hp->_a[0];
}int HeapSize(Heap* hp)
{assert(hp);return hp->_size;
}int HeapEmpty(Heap* hp)
{assert(hp);return hp->_size == 0;  // 是空就返回1
}

4、堆的應用?

4.1? 堆排序

堆排序即利用堆的思想來進行排序，總共分為兩個步驟：
1. 建堆
????????如果排升序：建大堆；
????????如果排降序：建小堆；

2. 利用堆刪除思想來進行排序

如果我們想要排升序：

①首先我們需要利用上面所講到的建堆，建立一個有N個數據的大堆；

②再利用堆的刪除思想將堆頂的數據（最大）與最后一個數據（下標是N-1）交換，此時我們最大的數據就來到了最后（N-1的位置），這時我們就不用再需要去考慮最后一個元素了，因為最后一個元素已經是最大；

③再對前N-1個數據再次進行堆排序即可。

注意：此刻交換到堆頂的數據并不一定滿足大堆的性質，所以還需要對堆頂的數據進行向下調整，使得滿足大堆的性質。
?

int a[] = {20, 17, 4, 16, 5, 3};

下面是對上述數組的排序示意圖（藍色所標記的元素表明不用再考慮）:

代碼實現：?


void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustDown(HPDataType* a, int size,int parent)
{int child = 2 * parent + 1;while (child < size){if ((child + 1) < size && a[child + 1] > a[child])  // 找出左右孩子中較大一個{child++;}if (a[parent] < a[child])   // 如果孩子更大就交換，并且更新父節點與孩子節點{Swap(&a[parent], &a[child]);parent = child;child = 2 * parent + 1;} else     // 如果父節點更大表明不用再交換了 ，跳出循環{break;}}
}void HeapSort(int* a, int n)
{// 利用向下調整算法建立一個大堆for (int i = (n - 1-1) / 2; i >= 0; i--)  // n-1 是最后一個節點，（n-1-1）/2就是第一個非葉子節點{AdjustDown(a, n,i);}while(n>1)  //如果數據個數大于1個，才進行排序{Swap(&a[0], &a[n - 1]);   // 堆頂與最后一個元素進行交換n--;           // 每排好一個就不用再考慮最后一個元素，相當與堆的數據減少一個AdjustDown(a, n, 0); // 將堆頂的數據向下調整}
}

4.2?TOP-K問題

TOP-K問題：在許多數據中，求出前K個最大的元素或者最小的元素，一般情況下數據量都比較大。

比如：專業前10名、世界500強、富豪榜、游戲中前100的活躍玩家等。

對于Top-K問題，能想到的最簡單直接的方式就是排序，但是：如果數據量非常大，排序就不太可取了(可能數據量太大以至于不能一次性全部加載到內存中)。最佳的方式就是用堆來解決，基本思路如下：
1. 用數據集合中前K個元素來建堆
? ? ? ? 若求前k個最大的元素，則建小堆
? ? ? ? 若求前k個最小的元素，則建大堆

2. 用剩余的N-K個元素依次與堆頂元素來比較，不滿足條件則替換堆頂元素
將剩余N-K個元素依次與堆頂元素比完之后，堆中剩余的K個元素就是所求的前K個最小或者最大的元素。

解釋：當我們要求數據中最大的前K個時：

①我們需要建立一個K個元素的小堆，這樣就保證了堆頂的元素永遠是堆中最小的；

②建好小堆以后，我們就可以用后面的 N-K 元素分別來跟堆頂的元素比較，只要發現有元素比堆頂的元素大，就將堆頂的元素替換為該元素；

③再對該元素進行向下調整，再一次找出堆中最小的元素到堆頂；

④一直循環上面的步驟，這樣就保證了最大的數據一定會被存儲在堆中。

代碼實現：


void AdjustDown(HPDataType* a, int size,int parent)
{int child = 2 * parent + 1;while (child < size){if ((child + 1) < size && a[child + 1] < a[child])  // 找出左右孩子中較大一個{child++;}if (a[parent] > a[child])   // 如果孩子更大就交換，并且更新父節點與孩子節點{Swap(&a[parent], &a[child]);parent = child;child = 2 * parent + 1;} else     // 如果父節點更大表明不用再交換了 ，跳出循環{break;}}
}void PrintTopK(int* a, int n, int k)
{// 1. 建堆--用a中前k個元素建堆for (int i = (k - 2) / 2; i >= 0; i--){AdjustDown(a, k, i);}// 2. 將剩余n-k個元素依次與堆頂元素交換，不滿則則替換for (int i = k; i < n; i++){if (a[i] > a[0])  // 如果后面的 N-K 個元素中有大于堆頂元素的，就替換堆定的數據{a[0] = a[i];AdjustDown(a, k, 0); // 將堆頂數據向下調整，保證小堆的性質}}// 前K個元素就是最大的K個元素for (int i = 0; i < k; i++){printf("%d ", a[i]);}
}

?四、二叉樹鏈式結構的實現

1、前置說明

????????在學習二叉樹的基本操作前，首先需先要創建一棵二叉樹，然后才能學習其相關的基本操作。但二叉樹的創建是一個很復雜的過程，下面我們先手動快速創建一棵簡單的二叉樹，快速進入二叉樹操作學習。

typedef int BTDataType;typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;BTNode* BuyNode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("BuyNode:malloc");exit(-1);}node->_data = x;node->_left = node->_right = NULL;
}BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->_left = node2;node1->_right = node4;node2->_left = node3;node4->_left = node5;node4->_right = node6;return node1;
}

再看二叉樹基本操作前，再回顧下二叉樹的概念，二叉樹是：
????????1. 一顆空樹；
????????2. 非空樹：根結點+根結點的左子樹+根結點的右子樹。

下面是上面我們創建的二叉樹示意圖：

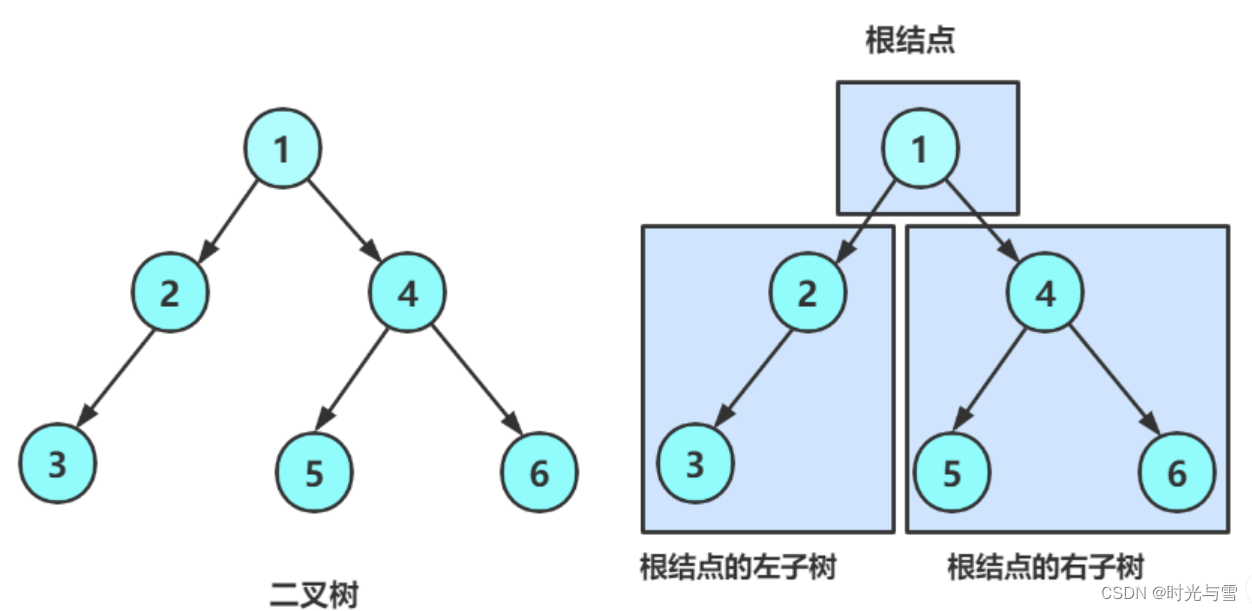
?2、二叉樹的遍歷

2.1 二叉樹的前、中、后序遍歷

????????學習二叉樹結構，最簡單的方式就是遍歷。所謂二叉樹遍歷(Traversal)是按照某種特定的規則，依次對二叉樹中的結點進行相應的操作，并且每個結點只操作一次。訪問結點所做的操作依賴于具體的應用問題。 遍歷是二叉樹上最重要的運算之一，也是二叉樹上進行其它運算的基礎。

規則：

????????1. 前序遍歷(Preorder Traversal 亦稱先序遍歷)——訪問根結點的操作發生在遍歷其左右子樹之前(先訪問根節點，再訪問左節點，再訪問右節點)。
????????2. 中序遍歷(Inorder Traversal)——訪問根結點的操作發生在遍歷其左右子樹之中（間）（先訪問左節點，再訪問根節點，再訪問右節點）。
????????3. 后序遍歷(Postorder Traversal)——訪問根結點的操作發生在遍歷其左右子樹之后（先訪問左節點，再訪問右節點，再訪問根節點）。

????????由于被訪問的結點必是某子樹的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解釋為根、根的左子樹和根的右子樹。NLR、LNR和LRN分別又稱為先根遍歷、中根遍歷和后根遍歷。

代碼實現：

// 前序遍歷
void BinaryTreePrevOrder(BTNode* root) // 根 -> 左子樹 -> 右子樹
{if (root == NULL)  // 節點為空就返回return;putchar(root->_data); // 不為空就先訪問該節點，再訪問左節點，最后訪問右節點BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}// 中序遍歷
void BinaryTreeInOrder(BTNode* root) // 左子樹 -> 根 -> 右子樹
{if (root == NULL)// 節點為空就返回return;BinaryTreePrevOrder(root->_left); // 不為空就先訪問左節點，再訪問該節點，最后訪問右節點putchar(root->_data);BinaryTreePrevOrder(root->_right);
}// 后序遍歷
void BinaryTreePostOrder(BTNode* root) // 左子樹 -> 右子樹 -> 根
{if (root == NULL) // 節點為空就返回return;BinaryTreePrevOrder(root->_left); // 不為空就先訪問左節點，再訪問右節點，最后訪問該節點BinaryTreePrevOrder(root->_right);putchar(root->_data);
}

2.2 二叉樹的層序遍歷

層序遍歷：除了先序遍歷、中序遍歷、后序遍歷外，還可以對二叉樹進行層序遍歷。設二叉樹的根結點所在層數為1，層序遍歷就是從所在二叉樹的根結點出發，首先訪問第一層的樹根結點，然后從左到右訪問第2層上的結點，接著是第三層的結點，以此類推，自上而下，自左至右逐層訪問樹的結點的過程就是層序遍歷。

例如下圖：訪問的結果就是 : A->B->C->D->E->F->G->H->I

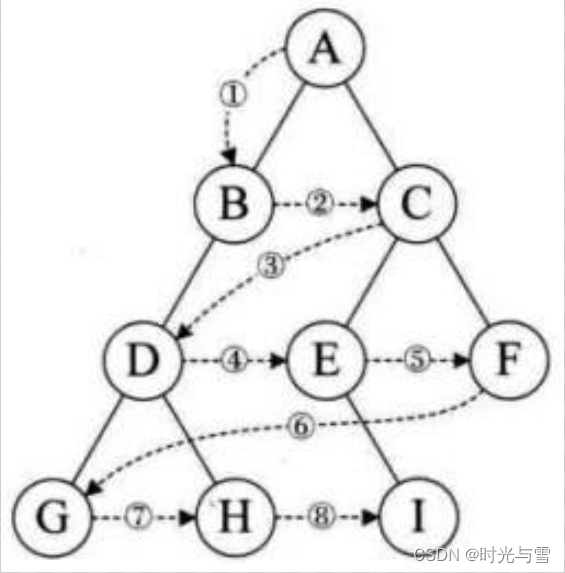
那么怎樣才能做到這樣的效果呢？答案是用“隊列”。利用隊列先進先出的功能就能很好的實現。

①創建一個空隊列，并將第一個節點插入到隊列；

②檢測隊列是否為空，若為空就停止，說明遍歷完成；若不為空就出隊列的第一個節點，并將該節點的左右節點（左右節點不為空時才入隊列）都插入隊列（先入左節點，再入右節點）；

③一直循環步驟②，直至隊列為空，說明遍歷已經完成。?

代碼實現：

void BinaryTreeLevelOrder(BTNode* root)
{Queue q;  // 創建一個隊列QueueInit(&q);  // 隊列初始化if (root)  // 如果樹不為空就將根節點插入隊列{QueuePush(&q, root);}while (!QueueEmpty(&q))  // 判斷隊列是否為空，不為空就繼續遍歷{BTNode* front = QueueFront(&q);  // 出隊列QueuePop(&q);       printf("%c ", front->_data);  // 訪問該節點if(front->_left)  // 如果存在左子樹就插入隊列QueuePush(&q, front->_left);if(front->_right)   // 如果存在右子樹就插入隊列QueuePush(&q, front->_right);}QueueDestroy(&q); // 隊列的銷毀
}

?3、二叉樹結點個數以及高度等

// 二叉樹的節點個數
int BinaryTreeSize(BTNode* root)
{if (root == NULL) // 該節點為空就返回 0；return 0;// 該節點不為空就返回  左樹的節點個數+右樹的節點個數+1；return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}// 二叉樹葉子結點個數
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL) // // 該節點為空就返回 0;return 0;// 該節點不為空，并且左右子樹都為空，說明該節點是葉子結點if (root->_left == NULL && root->_right == NULL)return 1;// 否則返回  左樹的葉子結點+右樹的葉子結點return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}// 二叉樹第k層結點個數
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL) // 如果為空就返回0return 0;if (k == 1) // k == 1,并且該節點不為空，說明該節點屬于第K層節點return 1;// 否則返回  左樹的K-1層節點+右樹的K-1層節點return BinaryTreeLevelKSize(root->_left  , k - 1) +BinaryTreeLevelKSize(root->_right, k - 1);
}int Max(int x, int y)
{return x > y ? x : y;
}
// 二叉樹的高度
int BinaryTreeHeight(BTNode* root)
{if (root == NULL) //節點為空就返回 0； return 0;// 否則返回 左子樹的高度與右子樹的高度的較大值 + 1 return Max(BinaryTreeHeight(root->_left), BinaryTreeHeight(root->_right)) + 1;
}// 二叉樹查找值為x的結點
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)  // 如果該節點為空，說明不在該節點return NULL;if (root->_data == x) // 如果找到了就返回 該節點return root;// 否則先在左樹找，如果左樹找到了，就返回；// 左樹倘若沒找到，就去右樹找，并返回右數找到的結果BTNode* node = BinaryTreeFind(root->_left, x);  //左樹找if(node)   // node 不為空說明找到了return node;   // 左樹找到了就返回// 左樹沒找到就去右樹里面找，無論右樹找沒找到都返回該結果return BinaryTreeFind(root->_right, x);  
}

4、二叉樹的創建和銷毀

// 通過前序遍歷的數組"ABD##E#H##CF##G##"構建二叉樹
// 其中 ‘#’表示空節點//數組 a  元素個數 n  元素下標 pi
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{// 如果元素下標超出數組的返回就返回空// 1、如果遇到‘#’(空節點）就++下標i，并返回NULLif (*pi >= n || a[*pi] == '#'){(*pi)++;return NULL;}// 2、正常情況下BTNode* node = (BTNode*)malloc(sizeof(BTNode));node->_data = a[*pi];(*pi)++;   // 每放入一個數據就++下標i；node->_left = BinaryTreeCreate(a, n, pi);node->_right = BinaryTreeCreate(a, n, pi);return node;
}// 二叉樹銷毀
void BinaryTreeDestory(BTNode** root)
{if (*root)  // 節點不為空{BinaryTreeDestory(&(*root)->_left);  // 先釋放左子樹BinaryTreeDestory(&(*root)->_right);//再釋放右子樹free(*root); //再釋放根節點*root = NULL;}
}

5、判斷二叉樹是否是完全二叉樹

? ? ? ? 這里如何判斷是否是完全二叉樹與上面層序遍歷的方法十分類似，大致分為下面幾步：

?完全二叉樹的定義：若某二叉樹的高度為 K ，且前 K-1 層是一個滿二叉樹，第K層的節點從左至右依次存放，則該二叉樹是完全二叉樹。

說明：完全二叉樹前K-2層的節點左右孩子都不為空；第K-1層的節點存在3種情況：

①左孩子右孩子都存在；②左孩子存在，右孩子不存在；③左右孩子都不存在。

示意圖：

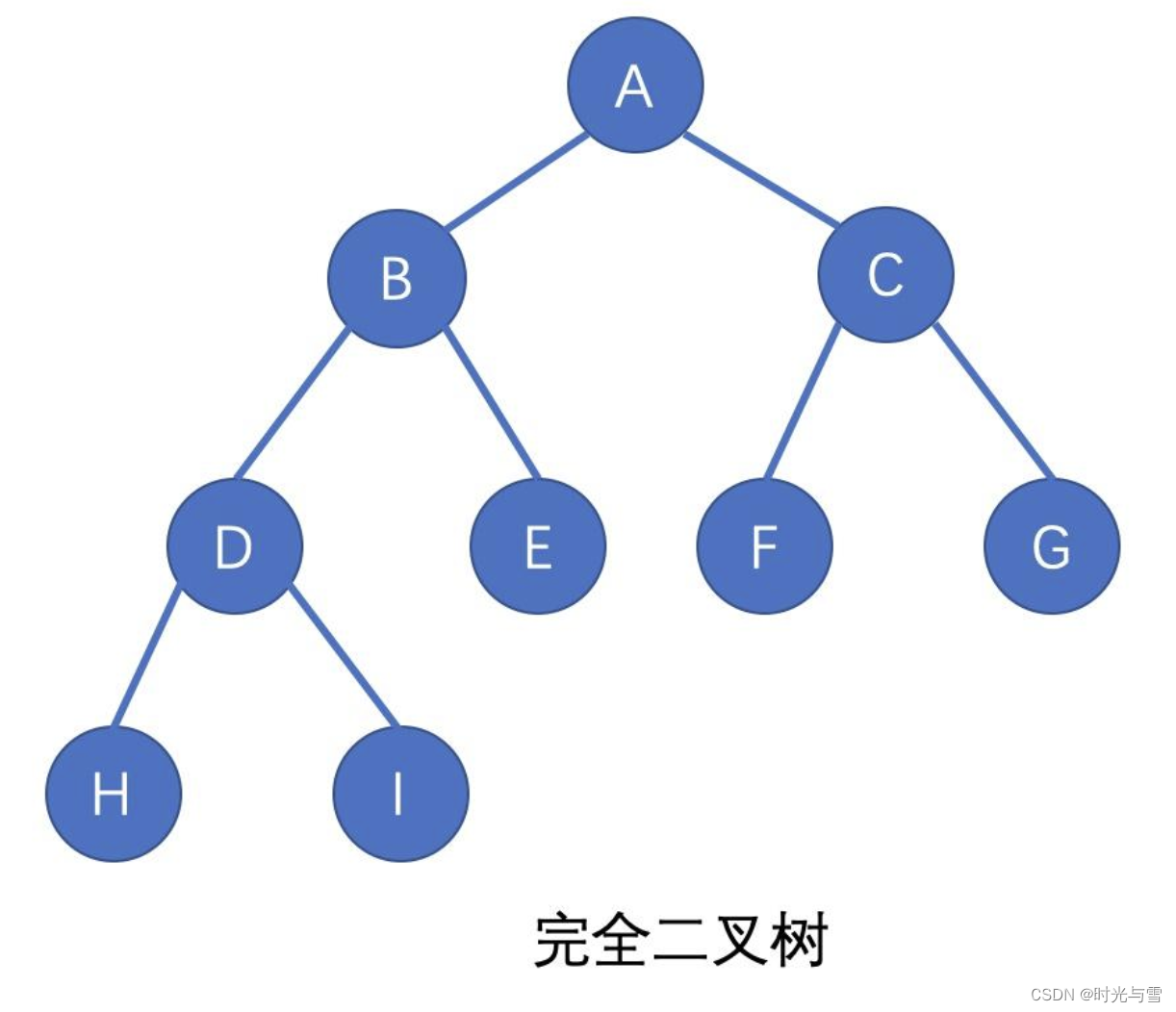
解題思路：

①創建一個空隊列，并將第一個節點插入到隊列；

②檢測隊列是否為空，若為空就停止，說明遍歷完成；若不為空就出隊列的第一個節點，并將該節點的左右節點（左右節點為空也要入隊列）都插入隊列（先入左節點，再入右節點）。

③重復步驟②，當出隊列的節點為空節點時就結束遍歷；若該樹滿足完全二叉樹的結構，則在隊列中，該空節點后的所有節點都是空節點；若不滿足二叉樹結構，則該空節點后一定存在非空節點。

例如上面的完全二叉樹出隊列時的狀態圖：

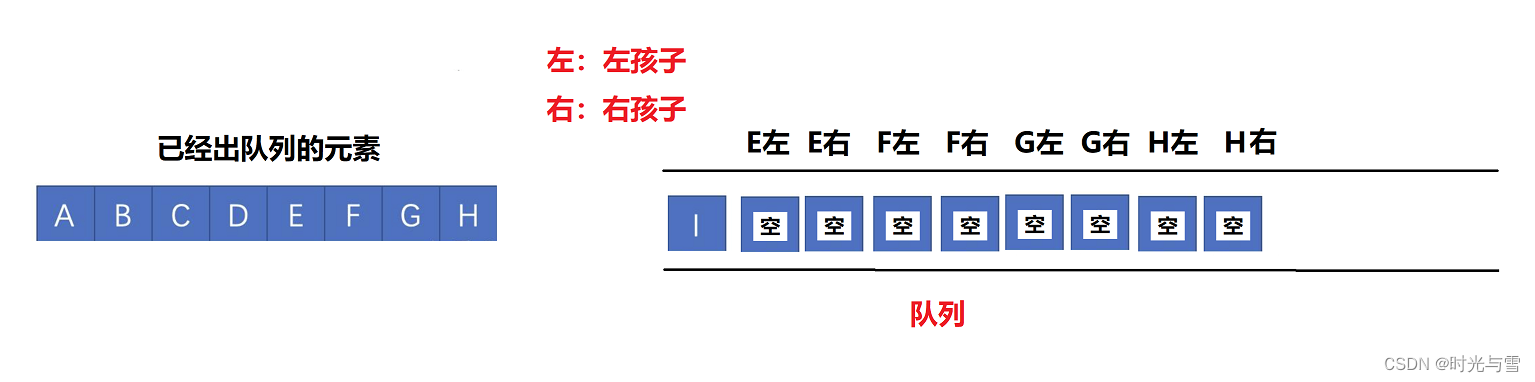
如果在上面的完全二叉樹中F節點的左邊添加一個節點 “J” ，那么該樹就不滿足完全二叉樹的結構，它的出隊列時的狀態圖將發生改變：

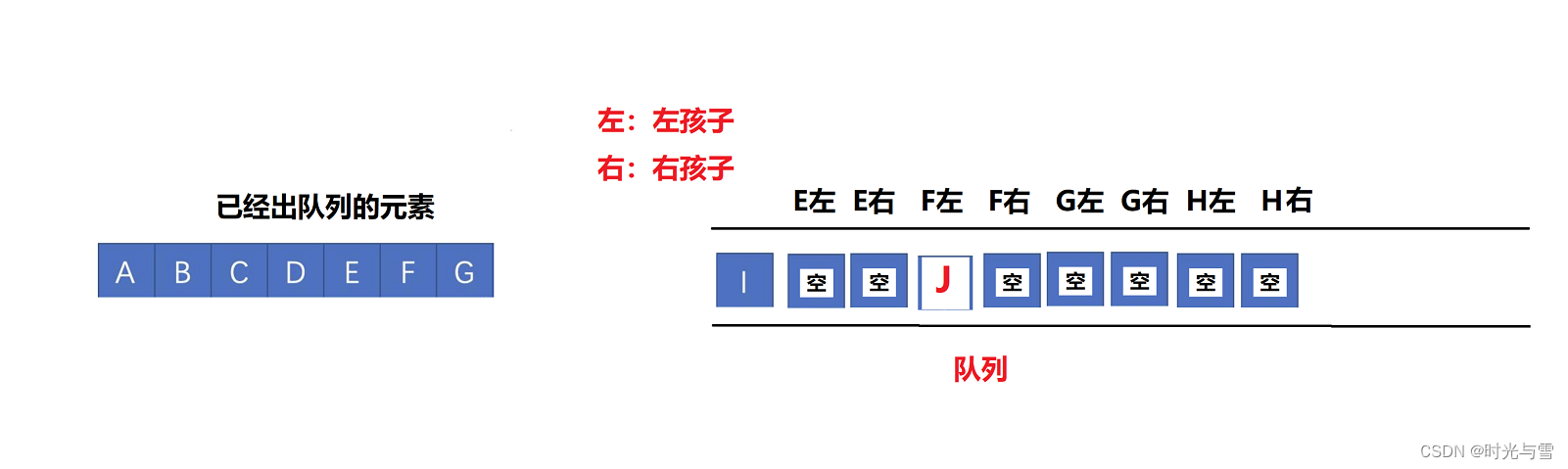
④從該空節點開始，向后訪問隊列中的各個節點，若隊列中還存在不為空的節點，則該樹不是完全二叉樹；若隊列中的節點都為空節點，則說明該樹是完全二叉樹。

代碼實現：

int BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL)  // 如果取出的節點是空節點就跳出循環{break;}QueuePush(&q, front->_left);  // 不是空節點就插入它的左節點與右節點QueuePush(&q, front->_right);}while (!QueueEmpty(&q))  // 從第一個空節點往后遍歷{BTNode* front = QueueFront(&q);QueuePop(&q);if (front)  // 如果存在不為空的節點，說明不是完全二叉樹{QueueDestroy(&q);return 0;}}//  沒有非空節點就返回 1return 1;QueueDestroy(&q);
}