目錄
一、數組的定義
1.1概念
1.2抽象數據類型定義
二、數組的順序存儲
2.1一維數組元素的存儲位置
2.2二維數組元素的存儲位置
2.3三維數組元素的存儲位置
三、特殊矩陣的壓縮存儲
3.1相關概念
3.2對稱矩陣
3.3三角矩陣
3.4對角矩陣(帶狀矩陣)
3.5稀疏矩陣
一、數組的定義
1.1概念
數組是按一定格式排列起來的具有相同類型的數據元素的集合
·聲明格式: 數據類型 變量名稱[長度];
例:int num[5]={0,1,2,3,4};
1.2抽象數據類型定義
ADT Array{
數據對象:j(i)=0,... b(i)-1, i=1,2,.....,n
????????????????? D={a(j1j2....j(n)) | a(j1j2.....j(n)) ∈ElemSet}
數據關系:R1={<a(j1...j(i)...j(n),a(j1...j(i+1)...j(n))> | 0<=j(k)<=b(k)-1,1<=k<=n,且k≠i,0<=j(i)<=b(k)-2, a(j1...j(i)...j(n)), a(j1...j(i+1)...j(n) ∈D,i=2,...,n}
基本操作:
①InitArray(&A,n,bound1,...boundn)?? //構造數組A
②DestroyArray(&A)?? //銷毀數組A
③Value(A,&e,index1,...,indexn)?? //取數組元素值
④Assign(A,&e,index1,...indexn)? //給數組元素賦值
}ADT Array
二、數組的順序存儲
2.1一維數組元素的存儲位置
LOC(i)=LOC(0)=a,i=0;
LOC(i)=LOC(i-1)+L=a+i*L,i>0
例:每個元素占4字節,假設a[0]存儲在2000單元,則a[3]地址為:2000+3*4=2012單元
?2.2二維數組元素的存儲位置
我們先來討論一下二維數組的存儲方式:
①以行序為主序
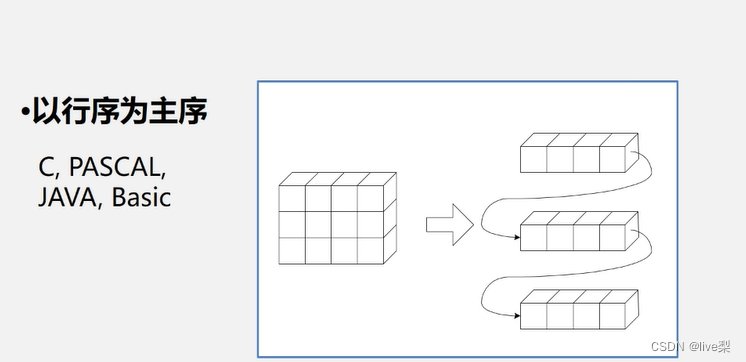
②以列序為主序


二維數組元素的存儲位置:(行優先的順序存儲)
a[i][j]的存儲位置:LOC(i,j)=LOC(0,0)+(n*i+j)*L
(n*i+j)表示在a[i][j]前面所有元素個數
例:

2.3三維數組元素的存儲位置
我們一樣先討論三位數組的存儲方式:


三位數組元素的存儲位置

三、特殊矩陣的壓縮存儲
3.1相關概念
①什么是壓縮存儲:
為多個相同的非零元素只分配一個存儲空間;對零元素不分配空間。
②什么樣的矩陣能夠壓縮:
對稱矩陣、對角矩陣、三角矩陣、稀疏矩陣
③什么叫稀疏矩陣:
矩陣中非零元素的個數較少(一般少于 5%)
3.2對稱矩陣
①特點:a(ij)=a(ji)
②存儲方法:只存儲下(或者上)三角(包括主對角線)的數據元素,共占用n(n+1)/2個元素空間。

③存儲結構:可以以行序為主序將元素存放在一個一維數組sa[n(n+1)/2]中
例:以行序為主序存儲下三角
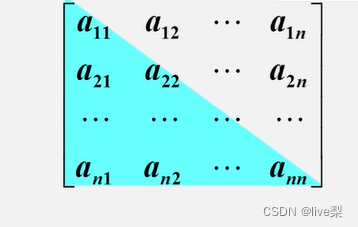

k表示元素a(ij)前面有幾個元素個數
k=1+2+3+4+...+(i-1)+(j-1) (i-1表示a(ij)前面有i-1行,j-1表示在a(ij)本行前面有幾個元素)
以a(n1)為例:k=1+2+3+...+(n-1)+(1-1)=n(n-1)/2
3.3三角矩陣
①特點:對角線以下(或者以上)的數據元素(不包括對角線)全部為常數c

②存儲方法:重復元素c共享一個元素存儲空間,共占用n(n+1)/2+1個元素(1表示常數c的存儲空間)
③存儲結構:將元素存放在一個一維數組sa[n(n+1)/2+1]中
·對于上三角矩陣:

·對于下三角矩陣:

k一樣表示a(ij)元素前面的元素個數
3.4對角矩陣(帶狀矩陣)
①特點:在n×n方陣中所有非零元素都集中在以主對角線為中心的帶狀區域中,區域外的值全為0
常見的有三對角矩陣、五對角矩陣、七對角矩陣等

②存儲方法:以對角線的順序存儲

3.5稀疏矩陣
①特點:非零元較零元少,且分布沒有規律。
②存儲方法:三元組法、十字鏈表
③存儲結構:順序存儲、鏈式存儲
·三元組順序表法
(i,j,a(ij)) (行數,列數,元素值)+(總行數,總列數,非零元素總個數)
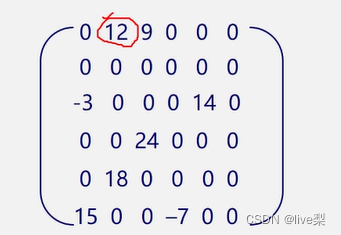

三元組法的優點:便于進行依行順序處理的矩陣運算;缺點:不能隨機存取。
改進:稀疏矩陣的鏈式存儲結構——十字鏈表
優點:能夠靈活地插入因運算而產生的新的非零元素,刪除因運算而產生的新的零元素
·十字鏈表
矩陣的每一個非零元素用一個結點表示,該結點除了(row,col,value)以外,還要有right、down兩個域。(right連接同一行中的下一個非零元素,down連接同一列中的下一個非零元素)
結構示意圖:

例:

引入頭指針:指向行或列中的第一個非零元素




















