前言
更詳細的在大佬的代碼隨想錄 (programmercarl.com)
本系列僅是簡潔版筆記,為了之后方便觀看
不同的二叉搜索樹
96. 不同的二叉搜索樹 - 力扣(LeetCode)
通過舉例子發現重疊子問題
代碼很簡單,主要是思路問題,知道二叉搜索樹的概念,并分別對左右子樹進行計算,相乘?
class Solution {
public:int numTrees(int n) {vector<int>dp(n+1);dp[0]=1;for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++){dp[i]+=dp[j-1]*dp[i-j];}}return dp[n];}
};01背包
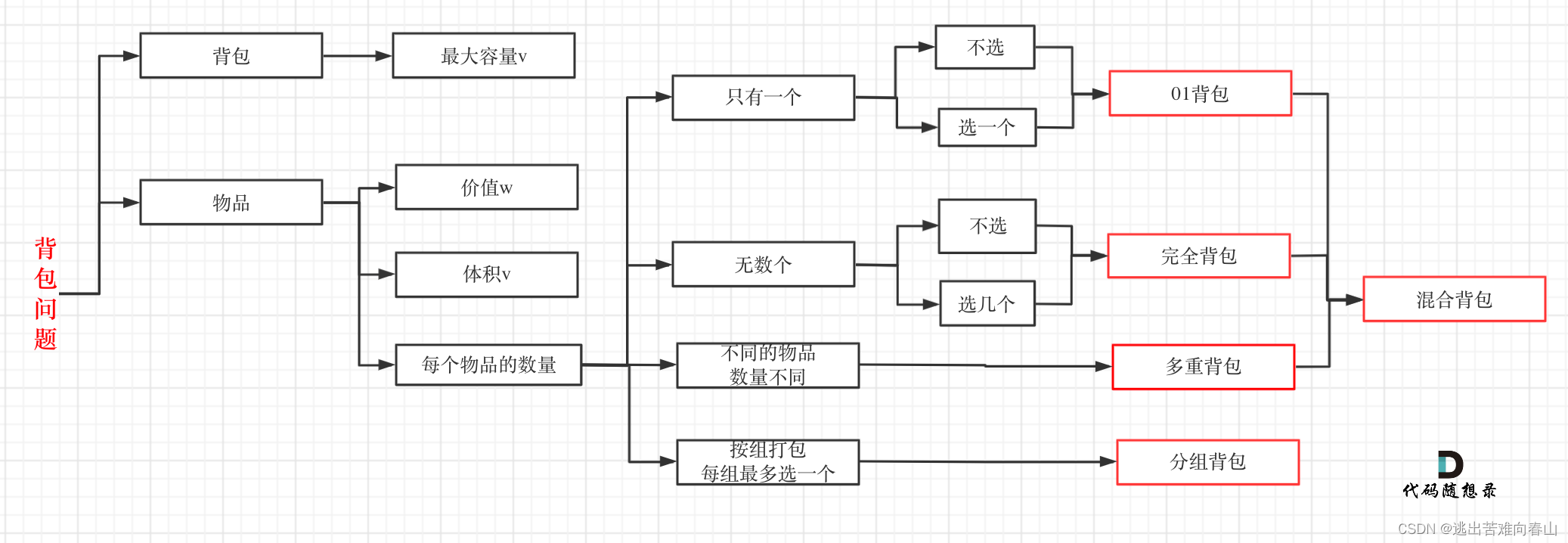
二維01背包
dp[i][j]表示 [0-i]的物品里任意取容量為j的背包的價值
- 不放物品i:dp[i][j]=dp[i - 1][j]
- 放物品i:dp[i][j]=dp[i - 1][j - weight[i]] + value[i]?
- 注意:非零下標不管初始化什么值,都不影響最后結果,但是有零下表初始化需要在注意
dp[0][j],當 j < weight[0]的時候,放不進去,dp[0][j] = 0;當j >= weight[0]時,dp[0][j] =value[0]
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0)); for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];}二維數組實現的dp01背包for循環可以顛倒
for(int i = 1; i < weight.size(); i++) { // 物品for(int j = 0; j <= bagweight; j++) { // 背包if (j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}}
一維01背包?
dp[j]容量為j的背包的價值
- 不放物品i:dp[j]=dp[j]
- 放物品i:dp[j]=dp[j - weight[i]] + value[i]?
- 注意:非零下標不管初始化什么值,都不影響最后結果,但是有零下標初始化為非負數的最小值0就可以
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0)); for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];}一維數組實現的dp01背包for循環不可以顛倒,背包必須倒序輸出,這樣才能符合每個背包只能使用一次
vector<int> dp(N + 1, 0);for (int i = 0; i < 物品數量; ++i) {for (int j = N; j >= costs[i]; --j) {dp[j] = max(dp[j], dp[j - costs[i]] + values[i]);}}
分割等和子集?
416. 分割等和子集 - 力扣(LeetCode)
把數組分割成兩個元素和相等的子集,可以弄成01背包問題,每個數只能使用一次,觀察是否能把num/2的背包容量給填滿
注意:本題重量和價值是統一變量
dp[j] == j 時集合中的子集總和正好可以湊成總和j
class Solution {
public:bool canPartition(vector<int>& nums) {int sum=0;vector<int>dp(10001,0);for(int i=0;i<nums.size();i++){sum+=nums[i];}if(sum%2==1) return false;//說明湊不成兩個一樣的數int target=sum/2;for(int i=0;i<nums.size();i++){for(int j = target; j >= nums[i]; j--) {dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);} }if (dp[target] == target) return true;return false; }
};最后一塊石頭的重量II
1049. 最后一塊石頭的重量 II - 力扣(LeetCode)
兩兩石頭相撞,最終取得最小差值,可以分成兩個數量之和相近的堆,來進行計算是上一題的演變,重量和價值是統一變量
target = sum / 2向下取整,所以sum - dp[target] >=dp[target],,所以最終結果就是用大的減去小的
class Solution {
public:int lastStoneWeightII(vector<int>& nums) {int sum=0;vector<int>dp(15001,0);for(int i=0;i<nums.size();i++){sum+=nums[i];}int target=sum/2;for(int i=0;i<nums.size();i++){for(int j = target; j >= nums[i]; j--) {dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);} }return sum - dp[target] - dp[target]; }
};目標和?
?494. 目標和 - 力扣(LeetCode)
一個集合分出兩個子集,加法left集合和減法right集合?
left- right = target。
left + right = sum
right = sum - left
left - (sum - left) = target
left = (target + sum)/2
targe,sum是固定的,所以就可以轉化為在集合nums中找出和為left的組合
class targetolution {
public:int findTargettargetumWays(vector<int>& nums, int target) {int sum = 0;for (int i = 0; i < nums.size(); i++) sum += nums[i];if (abs(target) > sum) return 0; if ((target + sum) % 2 == 1) return 0; int bagtargetize = (target + sum) / 2;vector<int> dp(bagtargetize + 1, 0);dp[0] = 1;for (int i = 0; i < nums.size(); i++) {for (int j = bagtargetize; j >= nums[i]; j--) {dp[j] += dp[j - nums[i]];}}return dp[bagtargetize];}
};一和零
474. 一和零 - 力扣(LeetCode)
dp[i][j]:最多有i個0和j個1的strs的最大子集的大小為dp[i][j]
for (int i = m; i >= zeroNum; i--) { for (int j = n; j >= oneNum; j--) {dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);}
}
















)

