
歸納編程學習的感悟,
記錄奮斗路上的點滴,
希望能幫到一樣刻苦的你!
如有不足歡迎指正!
共同學習交流!
🌎歡迎各位→點贊 👍+ 收藏? + 留言?📝
抱怨深處黑暗,不如提燈前行!

?
題目描述:
給你一個單鏈表的頭節點?head?,請你判斷該鏈表是否為回文鏈表。如果是,返回?true?;否則,返回?false?。
示例 1:

輸入:head = [1,2,2,1] 輸出:true
示例 2:
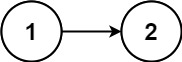
輸入:head = [1,2] 輸出:false
提示:
- 鏈表中節點數目在范圍
[1, 105]?內 0 <= Node.val <= 9
思路推導
判斷該鏈表是否為回文鏈表,數據范圍node.val<=9,節點數量∈[1,10^5]node.val <= 9, 節點數量 ∈ [1,10^5]node.val<=9,節點數量∈[1,10^5?]
可選方案1:轉數字,判斷是否為回文數
可選方案2:轉字符串,判斷是否為回文串
但這樣做就沒有利用到鏈表自身的性質,因此不是最合適的解法。
根據「206.反轉鏈表」的思路,可以在完成「鏈表前半部分的反轉」之后,通過雙指針指向前半部分的頭結點和后半部分鏈表的頭結點,每次推進一步并判斷數值是否相等。
但這存在「奇數節點個數的鏈表」和「偶數節點個數的鏈表」的前半部分和后半部分劃分上的不同的問題。
情況分析
回文鏈表必然會存在「奇數個節點」的鏈表和「偶數個節點」的鏈表。
對于長度為奇數的回文鏈表
1->2->3->2->1,長度為5的鏈表,那么從回文中心3向左右兩側出發,會遍歷得到相同的數字序列。
對于偶數長度的回文鏈表:
1->2->2->1,長度為4的鏈表,如果回文,那么從第2和第3個節點出發,向兩側掃描,可以得到相同的數字序列。
因此,假設節點個數為n
奇數鏈表:
回文中心為:(n+1)/2個節點
回文邊界為:(n+1)/2 - 1,(n+1)/2 + 1
偶數鏈表:
沒有回文中心
回文邊界:n/2和n/2 + 1
之后可以通過「統計節點個數」->「對奇偶鏈表需要翻轉的節點個數分別判斷完成前半部分反轉」->「從前半部分鏈表和后半部分鏈表的頭結點向兩側掃描推進判斷數字是否相同」的方法來判斷回文鏈表。
但目前這樣的考慮過于復雜了,因為實際上我們無需計算節點個數,只需要確定鏈表中間節點的位置即可。「確定鏈表中間節點的位置」的方法通常使用快慢指針法。
示例分析
設計雙指針slow = head, fast = head
「奇數鏈表」和「偶數鏈表」最終確定的中間節點不一致,我們可以先確定「鏈表中間節點位置」,再「反轉前半部分的鏈表」;也可以考慮在slow指針推進過程中完成「局部反轉」,這樣到達「中間位置節點」時恰好完成了前半部分的反轉。
- 偶數鏈表的示例分析:
局部翻轉還需要的變量pre以及變量初始化:
設計pre = null, slow = fast = head;
當前循環條件未知。
每次循環,slow指針每次前進一步,就翻轉局部鏈表,fast指針前進兩步。
偶數節點情況:
初始化:
null 1 -> 2 -> 2 -> 1 -> null^ ^
pre slow,fast
---------------------------------
第1輪循環
null<- 1 2 -> 2 -> 1 -> null^ ^ ^pre slow fast
---------------------------------
第2輪循環:
null<- 1 <- 2 2-> 1-> null^ ^ ^pre slow fast
第二次循環結束后,就已經完成了前半部分鏈表的反轉,
pre指向前半部分鏈表的第一個元素。
slow到達「中間節點的第二個節點」。
slow指針指向后半部分鏈表的第一個元素。
偶數鏈表的循環退出條件是 fast == null- 奇數鏈表的示例分析:
奇數鏈表模擬:
初始化
null 1 -> 2 -> 3 -> 2 -> 1 -> null^ ^
pre slow,fast
第一輪循環
null<- 1 2 -> 3 -> 2 -> 1 -> null^ ^ ^pre slow fast第二輪循環:
null<- 1 <- 2 3 -> 2 -> 1 -> null^ ^ ^pre slow fast
第二輪循環結束后,slow到達「鏈表中間節點」位置。
循環退出條件是 fast.next == null
循環退出時
fast = 鏈表最后一個元素
pre 指向前部分鏈表的第一個元素
slow 指針指向后部分鏈表的第一個元素。
需要特殊處理:即將slow指針向后推進一位,
以保證和「偶數鏈表」相同,slow指針指向后半部分回文鏈表的第一個元素。
- 抽取循環結束時的共性:
pre指向前半部分鏈表的第一個元素。
slow指針經過處理后,指向后半部分鏈表的首個元素
循環退出條件:
????????對于奇數鏈表為fast.next == null
????????對于偶數鏈表為fast==null
- 通過「奇數鏈表」和「偶數鏈表」的示例分析得到偽代碼:
循環開始:
1. 變量初始化
雙指針賦值slow = head, fast = head,
局部旋轉前一個變量指針pre = null
局部翻轉需要保存的下一個節點 tmp = null
2. 雙指針推進循環
循環條件(fast != null && fast.next != null){2.1 快指針每次推進兩步。2.2 慢指針通過「局部反轉」的方式進行指針的推進。
}
3.循環結束后的情況分析:3.1 偶數鏈表循環結束后,fast == null,pre指向前半部分第一個回文數slow指向后半部分第一個回文數3.2 奇數鏈表循環結束后,fast !=null, fast.next == nullpre指向前半部分第一個回文數slow指向后半部分第一個節點(鏈表中間節點)。為使得一致,slow指針需要指向第一個回文數需要將slow向前推進一步
因此,如果fast != null,將slow指針推進一步。
4. 此時pre指向前半部分鏈表第一個回文數,slow指向后半部分鏈表第一個回文數。
循環判斷:
循環條件:pre!= null || slow.next != null
向兩邊同時推進pre和slow,比較pre.val和slow.val是否相等,
如果pre.val != slow.val,說明不是回文數,返回false。
當pre和slow都推進到鏈表末尾,說明每個數都相等,返回true。
代碼實現:
/*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/
typedef struct ListNode LNode;
bool isPalindrome(struct ListNode* head) {LNode*fast;LNode*slow;fast=head;slow=head;while(fast&&fast->next){fast=fast->next->next;slow=slow->next;}LNode *temp,*pre,*cur;pre=NULL;cur=slow;while(cur){temp=cur->next;cur->next=pre;pre=cur;cur=temp;}LNode*p;p=head;while(pre&&p){if(p->val!=pre->val){break;}p=p->next;pre=pre->next;}if(p==NULL||pre==NULL){return true;}else{return false;}
}復雜度分析:
時間復雜度:O(n),雙指針掃描鏈表一遍O(n),局部反轉時間復雜度O(1),回文數比較時間復雜度O(n)。
空間復雜度:O(1),指針只占用了常量的空間。



















