題目
設計一個算法,用最少數量的矩形覆蓋一系列寬度為d、高度為w的矩形建筑物側墻,且矩形不能超出邊界。
核心思路
考慮這種結構
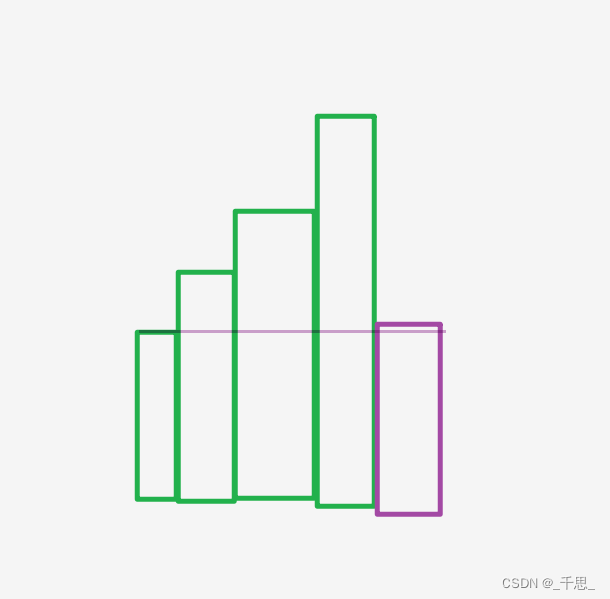
前面遞增后面一個與前面的某個高度一致,這時候考慮最下面的覆蓋(即都是從最下面向上覆蓋)
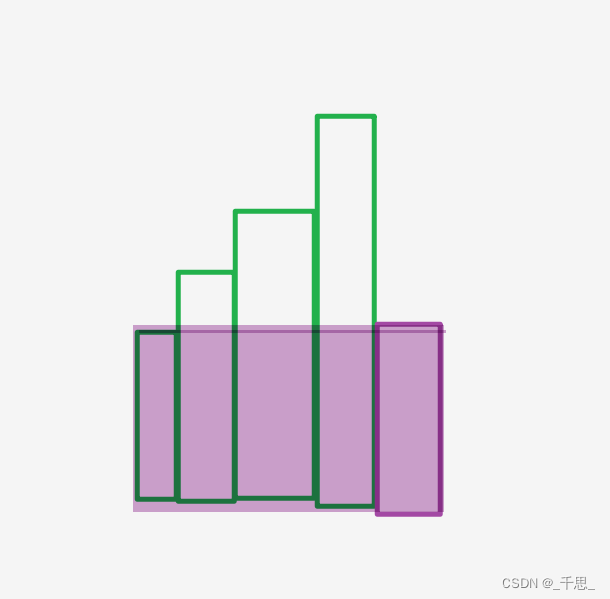
考慮到使用棧,這里我們用列表代替
當棧不為空并且新元素比棧頂小,這時候存在這種可能結構成立,
對每個墻循環,如果新元素比棧頂元素大,就進棧;
反之,如果新元素比棧頂元素小,就使得棧頂元素出棧,繼續比較新棧頂元素與當前使用新元素的大小,一直到比較到當前使用新元素和之前的某個元素的大小相同,此時計數器+1,表示找到這種結構+1
另外向上因為與數量一致,所以這里不考慮
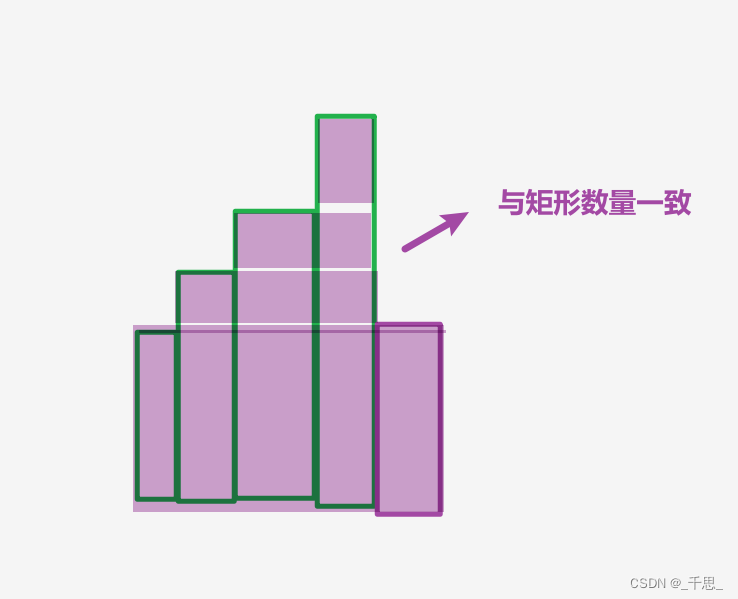
偽代碼
定義一個函數 main:定義一個變量 n,用于存儲輸入的整數。定義一個變量 ans,初始化為 0,用于存儲最終答案。定義一個空列表 st,用于模擬棧結構。對于從 1 到 n 的每個整數 i:讀取兩個整數 d 和 w,并將它們分別存儲到變量 d 和 w 中。當列表 st 不為空且 w 小于等于 st 中最后一個元素時:如果 st 中最后一個元素等于 w:將 ans 的值增加 1。從 st 中移除最后一個元素,因為當前 w 值破壞了遞增結構。將 w 添加到 st 的末尾。打印 n 減去 ans 的結果。如果這個腳本是主程序:調用 main 函數。CODE
def main():n = int(input())# 這種結構有多少種ans = 0st = []for i in range(1, n + 1):d, w = map(int, input().split())# 列表類似棧的結構while st and w <= st[-1]:# 找到該種結構種類數+1if st[-1] == w:ans += 1# pop掉,因為該種結構要求前面都是遞增,而這里當前使用新元素已經是破壞了# 遞增結構,所以直接丟掉,準備下一次的# 最后棧是空的,上面循環直接刷到最前面了st.pop()st.append(w)print(n - ans)if __name__ == "__main__":main()












)



:QStyle和自定義樣式)

