拿捏數據結構- 鏈式二叉樹

鏈式二叉樹的概念：

鏈式二叉樹解決的是非完全二叉樹解決不了的問題

什么意思呢，簡單的說就是，鏈式二叉樹

可以是下面三種二叉樹

但是非鏈式二叉樹只能是前兩種

鏈式二叉樹的存儲

節點結構：首先定義一個結構體或類來表示二叉樹的節點。每個節點通常包含三個部分：

  • 存儲數據的成員變量（例如，_data）。
  • 指向其左子節點的指針（例如，_left）。
  • 指向其右子節點的指針（例如，_right）。

鏈式二叉樹的存儲方式提供了很高的靈活性，可以輕松地添加和刪除節點，同時也使得樹結構的實現更加直觀和易于操作。

前序/中序/后序遍歷

講解鏈式二叉樹之前我們需要先了解一下，前序/中序/后序，因為在初階數據結構里，鏈式二叉樹我們是用遞歸的方式來實現的，非遞歸的方式，在后續篇章會進行講解。

這里我們上圖，假設是這一張圖

前序遍歷

前序遍歷的順序是：首先訪問根節點，然后遞歸地進行左子樹的前序遍歷，最后遞歸地進行右子樹的前序遍歷。

遍歷順序：根-左-右

步驟：

  1. 訪問當前節點。
  2. 遍歷左子樹。
  3. 遍歷右子樹。

示例： 假設有如下的二叉樹：

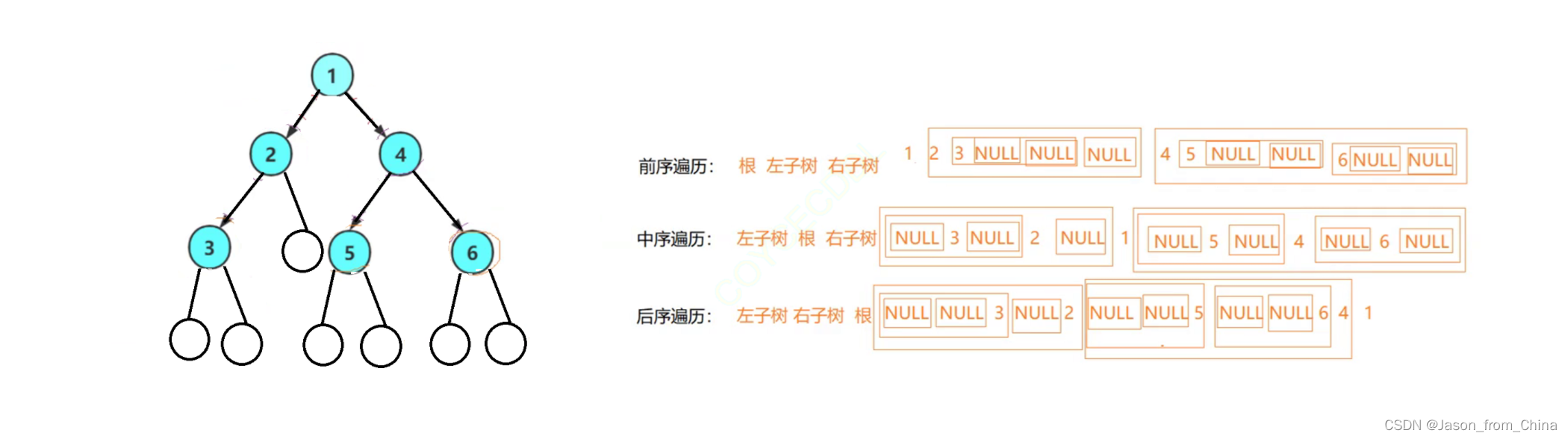
關于前序遍歷，我們需要把空節點也看出來

如圖

所以根據遍歷順便，我們應該是

1? 2? 3 NULL NULL NULL 4 5 NULL NULL 6 NULL NULL

中序遍歷

中序遍歷的順序是：首先遞歸地進行左子樹的中序遍歷，然后訪問根節點，最后遞歸地進行右子樹的中序遍歷。

遍歷順序：左-根-右

步驟：

  1. 遍歷左子樹。
  2. 訪問當前節點。
  3. 遍歷右子樹。

正確的是

后序遍歷

后序遍歷的順序是：首先遞歸地進行左子樹的后序遍歷，然后遞歸地進行右子樹的后序遍歷，最后訪問根節點。

遍歷順序：左-右-根

步驟：

  1. 遍歷左子樹。
  2. 遍歷右子樹。
  3. 訪問當前節點。

正確的是

總結

鏈式二叉樹的實現

創建文件

定義鏈式二叉樹結構

typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;

解釋：

  1. typedef int BTDataType; 這行代碼使用 typedef 關鍵字定義了一個新的別名 BTDataType，它是 int 類型的別名。這意味著在代碼中，你可以使用 BTDataType 作為 int 類型數據的一個更有意義的別名。

  2. typedef struct BinaryTreeNode 這行代碼開始定義一個名為 BinaryTreeNode 的新結構體類型。struct BinaryTreeNode 是結構體的名稱，它將用于表示二叉樹中的節點。

  3. BTDataType _data; struct BinaryTreeNode* _left; struct BinaryTreeNode* _right; } 這個大括號內的代碼定義了 BinaryTreeNode 結構體的具體內容：

    • BTDataType _data;?定義了一個名為?_data?的成員變量，它用于存儲節點中的數據。由于使用了之前定義的?BTDataType，所以這個成員變量是?int?類型的。
    • struct BinaryTreeNode* _left;?定義了一個名為?_left?的成員變量，它是一個指向?BinaryTreeNode?類型的指針，用于指向當前節點的左子節點。
    • struct BinaryTreeNode* _right;?定義了一個名為?_right?的成員變量，它也是一個指向?BinaryTreeNode?類型的指針，用于指向當前節點的右子節點。

  4. BTNode; 這行代碼為 BinaryTreeNode 結構體定義了一個易記的別名 BTNode。這樣，在代碼中就可以使用 BTNode 來聲明二叉樹的節點。

總結來說，這段代碼定義了一個用于表示鏈式二叉樹節點的結構體 BTNode，其中包含一個整型數據 _data 和兩個指向相同結構體類型的指針 _left 和 _right，分別用于存儲節點的數據和鏈接到左右子節點。通過這種定義，可以方便地創建和管理二叉樹數據結構。

二叉樹的初始化

//二叉樹的初始化
BTNode* BuyNode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("BinaryTreeInit:newnode:");exit(1);}newnode->_data = x;newnode->_left = NULL;newnode->_right = NULL;return newnode;
}

解釋：

  1. BTNode* BuyNode(BTDataType x)

    • 這是函數的聲明行，定義了一個名為?BuyNode?的函數，它接收一個類型為?BTDataType（之前定義的?int?類型別名）的參數?x，并返回一個指向?BTNode?類型的指針。

  2. BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));

    • 這行代碼使用?malloc?函數為新的二叉樹節點分配內存。sizeof(BTNode)?計算?BTNode?類型的大小，確保分配足夠的內存。分配成功后，newnode?指針將指向這塊新分配的內存。

  3. if (newnode == NULL)

    • 這行代碼檢查?malloc?是否成功分配了內存。如果?newnode?為?NULL，表示內存分配失敗。

  4. perror("BinaryTreeInit:newnode:");

    • 如果內存分配失敗，使用?perror?函數輸出錯誤信息到標準錯誤。"BinaryTreeInit:newnode:"?是自定義的錯誤前綴，后跟系統定義的錯誤信息。

  5. exit(1);

    • 緊接著，使用?exit?函數以狀態碼?1?退出程序。狀態碼?1?通常表示程序因錯誤而終止。

  6. newnode->_data = x;

    • 如果內存分配成功，這行代碼將參數?x?的值賦給新節點的?_data?成員變量，從而初始化節點存儲的數據。

  7. newnode->_left = NULL;

    • 這行代碼將新節點的?_left?指針設置為?NULL，表示當前沒有左子節點。

  8. newnode->_right = NULL;

    • 類似地，這行代碼將新節點的?_right?指針設置為?NULL，表示當前沒有右子節點。

  9. return newnode;

    • 最后，函數返回指向新創建并初始化的?BTNode?節點的指針。

總結來說，BuyNode 函數負責創建一個新的二叉樹節點，初始化其數據和子節點指針，如果內存分配失敗，則輸出錯誤信息并終止程序。這個函數是構建二叉樹時用于生成節點的基本工具。

這里的關鍵點是認識到 ，左右節點的存在

二叉樹的銷毀

這里就采取了遞歸，開始上難度了，這里我先不做講解，模擬創建二叉樹之后我們進行講解遞歸

// 二叉樹銷毀
void BinaryTreeDestory(BTNode* root)
{if (root == NULL){return;}BinaryTreeDestory(root->_left);BinaryTreeDestory(root->_right);free(root);
}

解釋：

  1. void BinaryTreeDestory(BTNode* root)

    • 這是函數的聲明行，定義了一個名為?BinaryTreeDestory?的函數，它接收一個指向?BTNode?類型的指針?root?作為參數。該函數沒有返回值（void?類型）。

  2. if (root == NULL)

    • 這行代碼檢查傳入的?root?指針是否為?NULL。如果是?NULL，表示二叉樹為空或已經被銷毀，因此函數直接返回。

  3. BinaryTreeDestory(root->_left);

    • 如果?root?不是?NULL，這行代碼首先遞歸調用?BinaryTreeDestory?函數，傳入當前節點的左子節點?root->_left?作為參數。這樣做會先銷毀左子樹。

  4. BinaryTreeDestory(root->_right);

    • 接著，這行代碼遞歸調用?BinaryTreeDestory?函數，傳入當前節點的右子節點?root->_right?作為參數。這會銷毀右子樹。

  5. free(root);

    • 在左子樹和右子樹都被銷毀之后，這行代碼使用?free?函數釋放當前節點?root?所占用的內存。

總結來說，BinaryTreeDestory 函數通過遞歸的方式，先銷毀二叉樹的左子樹和右子樹，然后釋放根節點的內存。這種銷毀方式確保了二叉樹中的所有節點都會被釋放，避免了內存泄漏。需要注意的是，在使用這種銷毀方式時，確保在銷毀二叉樹后不再使用任何指向該樹的指針，因為整個樹的內存已經被釋放。

模擬簡易鏈式二叉樹

//構建二叉樹
void teer()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);//BTNode* node7 = BuyNode(7);node1->_left = node2;node2->_left = node3;node1->_right = node4;node4->_left = node5;node4->_right = node6;//node2->_right = node7;}
int main()
{//構建二叉樹teer();return 0;
}

這里我們模擬實現一個二叉樹

就是這樣

前序遍歷實現

// 二叉樹前序遍歷 
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}

解釋：

  1. void BinaryTreePrevOrder(BTNode* root)

    • 這是函數的聲明行，定義了一個名為?BinaryTreePrevOrder?的函數，它接收一個指向?BTNode?類型的指針?root?作為參數。該函數沒有返回值（void?類型）。

  2. if (root == NULL)

    • 這行代碼檢查傳入的?root?指針是否為?NULL。如果是?NULL，表示當前節點為空，不需要遍歷。

  3. printf("NULL ");

    • 如果當前節點為空，打印字符串?"NULL "?到標準輸出。這是一種表示空節點的常見做法，但在實際應用中，通常會省略這一步，或者用其他方式處理空節點。

  4. printf("%d ", root->_data);

    • 如果當前節點不為空，這行代碼會打印當前節點的?_data?成員變量的值。%d?是格式化輸出的占位符，表示后面跟著的參數是一個整數。

  5. BinaryTreePrevOrder(root->_left);

    • 這行代碼遞歸調用?BinaryTreePrevOrder?函數，傳入當前節點的左子節點?root->_left?作為參數。這將執行左子樹的前序遍歷。

  6. BinaryTreePrevOrder(root->_right);

    • 最后，這行代碼遞歸調用?BinaryTreePrevOrder?函數，傳入當前節點的右子節點?root->_right?作為參數。這將執行右子樹的前序遍歷。

總結來說，BinaryTreePrevOrder 函數通過遞歸的方式實現了二叉樹的前序遍歷。它首先打印當前節點的值，然后遞歸地遍歷左子樹，最后遞歸地遍歷右子樹。這種遍歷方式在樹的遍歷、搜索、復制等操作中非常有用。

圖解：

??

中序遍歷實現

// 二叉樹中序遍歷
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}BinaryTreeInOrder(root->_left);printf("%d ", root->_data);BinaryTreeInOrder(root->_right);
}

解釋：

  1. void BinaryTreeInOrder(BTNode* root)

    • 這是函數的聲明行，定義了一個名為?BinaryTreeInOrder?的函數，它接收一個指向?BTNode?類型的指針?root?作為參數。該函數沒有返回值（void?類型）。

  2. if (root == NULL)

    • 這行代碼檢查傳入的?root?指針是否為?NULL。如果是?NULL，表示當前節點為空，不需要遍歷。

  3. printf("NULL ");

    • 如果當前節點為空，打印字符串?"NULL "?到標準輸出。這通常用于表示空節點，但在實際的中序遍歷中，通常會忽略空節點而不是打印它們。

  4. BinaryTreeInOrder(root->_left);

    • 這行代碼遞歸調用?BinaryTreeInOrder?函數，傳入當前節點的左子節點?root->_left?作為參數。這將執行左子樹的中序遍歷。

  5. printf("%d ", root->_data);

    • 在左子樹遍歷之后，這行代碼打印當前節點的?_data?成員變量的值。因為在左子樹遍歷之后訪問根節點，所以對于二叉搜索樹來說，這會保證按升序打印節點值。

  6. BinaryTreeInOrder(root->_right);

    • 最后，這行代碼遞歸調用?BinaryTreeInOrder?函數，傳入當前節點的右子節點?root->_right?作為參數。這將執行右子樹的中序遍歷。

后序遍歷實現

// 二叉樹后序遍歷
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}BinaryTreePostOrder(root->_left);BinaryTreePostOrder(root->_right);printf("%d ", root->_data);
}

解釋：

  1. void BinaryTreePostOrder(BTNode* root)

    • 這是函數的聲明行，定義了一個名為?BinaryTreePostOrder?的函數，它接收一個指向?BTNode?類型的指針?root?作為參數。該函數沒有返回值（void?類型）。

  2. if (root == NULL)

    • 這行代碼檢查傳入的?root?指針是否為?NULL。如果是?NULL，表示當前節點為空，不需要遍歷。

  3. printf("NULL ");

    • 如果當前節點為空，打印字符串?"NULL "?到標準輸出。這通常用于表示空節點，但在實際的后序遍歷中，通常會忽略空節點而不是打印它們。

  4. BinaryTreePostOrder(root->_left);

    • 這行代碼遞歸調用?BinaryTreePostOrder?函數，傳入當前節點的左子節點?root->_left?作為參數。這將執行左子樹的后序遍歷。

  5. BinaryTreePostOrder(root->_right);

    • 在左子樹遍歷之后，這行代碼遞歸調用?BinaryTreePostOrder?函數，傳入當前節點的右子節點?root->_right?作為參數。這將執行右子樹的后序遍歷。

  6. printf("%d ", root->_data);

    • 在左子樹和右子樹都遍歷之后，這行代碼打印當前節點的?_data?成員變量的值。因為這是在訪問完左右子樹之后的操作，所以它是后序遍歷的一部分。

二叉樹節點個數

什么是節點個數，也就是，全部節點個數

// 二叉樹節點個數
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}

解釋：

  1. int BinaryTreeSize(BTNode* root)

    • 這是函數的聲明行，定義了一個名為?BinaryTreeSize?的函數，它接收一個指向?BTNode?類型的指針?root?作為參數。函數返回一個整數值，表示樹中的節點總數。

  2. if (root == NULL)

    • 這行代碼檢查傳入的?root?指針是否為?NULL。如果是?NULL，表示當前節點為空，不計入節點總數。

  3. return 0;

    • 如果當前節點為空，函數返回?0。這是遞歸的基本情況，表示空樹的節點數為?0。

  4. return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;

    • 如果當前節點不為空，這行代碼遞歸調用自身兩次：一次計算左子樹的節點數?BinaryTreeSize(root->_left)，一次計算右子樹的節點數?BinaryTreeSize(root->_right)。然后將這兩個調用的結果相加，并加上?1?來表示當前節點本身。這樣，你就得到了整棵樹的節點總數。

圖解

二叉樹葉子節點個數

什么是葉子結點個數

也就是：

// 二叉樹葉子節點個數
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (BinaryTreeLeafSize(root->_left) == 0 && BinaryTreeLeafSize(root->_right) == 0)return 1;return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}

解釋：

  1. int BinaryTreeLeafSize(BTNode* root)

    • 這是函數的聲明行，定義了一個名為?BinaryTreeLeafSize?的函數，接收一個指向?BTNode?類型的指針?root?作為參數。函數返回一個整數值，表示樹中葉子節點的總數。

  2. if (root == NULL)

    • 這行代碼檢查傳入的?root?指針是否為?NULL。如果是?NULL，表示當前節點為空，不計入葉子節點的總數。

  3. return 0;

    • 如果當前節點為空，函數返回?0。這是遞歸的基本情況之一，表示空樹的葉子節點數為?0。

  4. if (BinaryTreeLeafSize(root->_left) == 0 && BinaryTreeLeafSize(root->_right) == 0)

    • 這行代碼是一個條件語句，用于檢查當前節點的左子節點和右子節點是否都為空。如果兩者都為空，那么當前節點就是一個葉子節點。

  5. return 1;

    • 如果當前節點是葉子節點，即它的左右子節點都為空，那么返回?1，表示葉子節點數為?1。

  6. return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);

    • 如果當前節點不是葉子節點，這行代碼遞歸調用自身兩次：一次計算左子樹的葉子節點數?BinaryTreeLeafSize(root->_left)，一次計算右子樹的葉子節點數?BinaryTreeLeafSize(root->_right)。然后將這兩個調用的結果相加，得到當前子樹的葉子節點總數。

總結來說，BinaryTreeLeafSize 函數通過遞歸的方式遍歷二叉樹，計算葉子節點的個數。它首先檢查當前節點是否為空，如果不是空，再檢查當前節點是否為葉子節點（左右子節點都為空），如果是葉子節點則計數 1，否則遞歸地計算左右子樹的葉子節點數并相加。這種方法可以正確地計算出任意二叉樹的葉子節點總數。

圖解

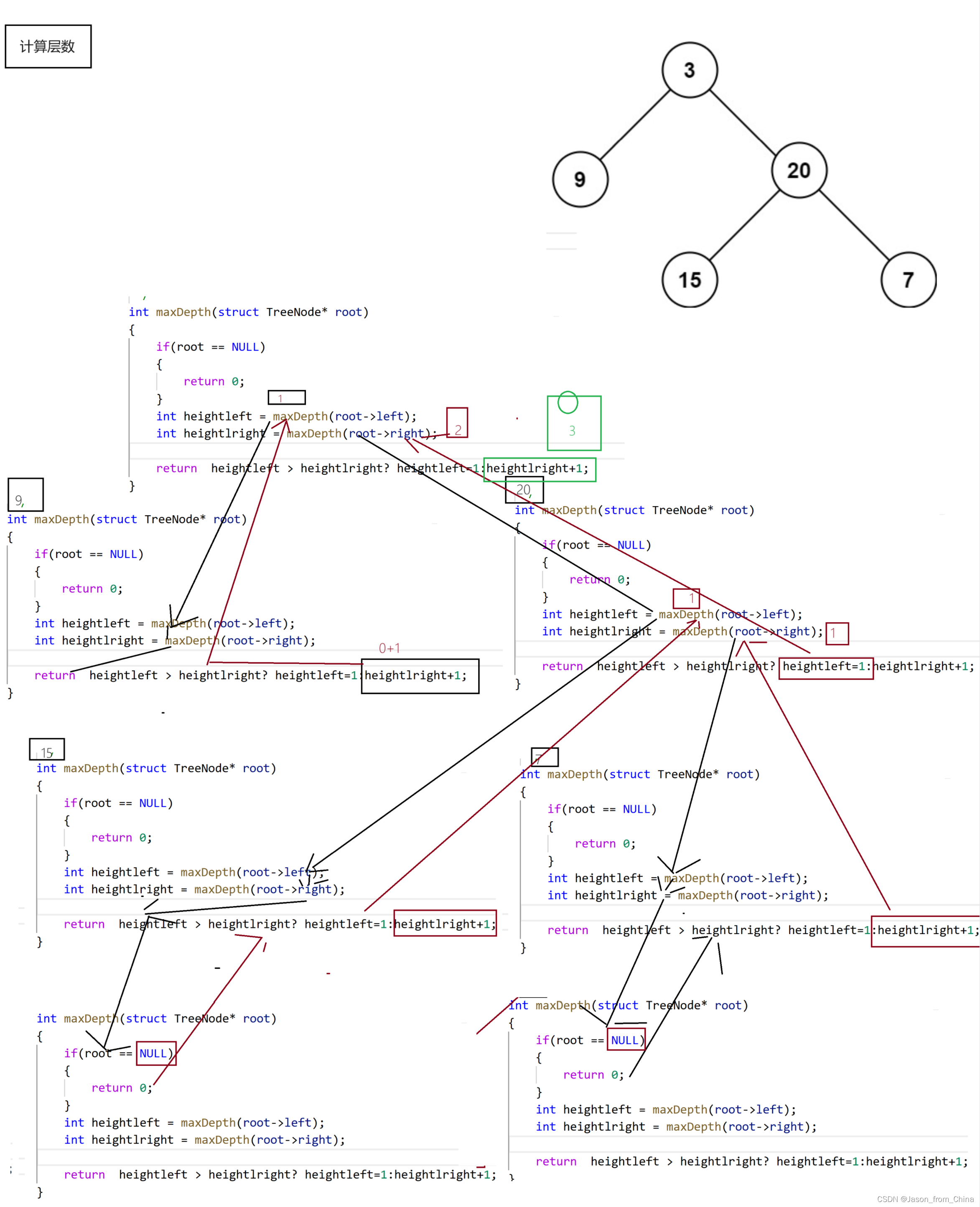
二叉樹高度

高度也就是二叉樹的層數

// 二叉樹高度
int BinaryTreeHeight(BTNode* root)
{ if (root == NULL){return 0;}int heightleft = BinaryTreeHeight(root->_left);int heightright = BinaryTreeHeight(root->_right);return heightleft >= heightright ? heightleft + 1 : heightright + 1;
}

這里的關鍵是理解如何遞歸地計算左子樹和右子樹的高度。

  1. int heightleft = BinaryTreeHeight(root->_left);

    • 這行代碼是對?BinaryTreeHeight?函數的遞歸調用，目的是計算當前節點的左子樹的高度。root->_left?是對當前節點左子節點的引用，如果左子節點存在，就對它調用?BinaryTreeHeight?函數，否則返回?0（如果左子節點為空）。

  2. int heightright = BinaryTreeHeight(root->_right);

    • 類似于上面的調用，這行代碼計算當前節點的右子樹的高度。root->_right?是對當前節點右子節點的引用，同樣地，如果右子節點存在，就對它調用?BinaryTreeHeight?函數，否則返回?0（如果右子節點為空）。

這里的關鍵點在于?? ?

int heightleft = BinaryTreeHeight(root->_left);
int heightright = BinaryTreeHeight(root->_right);

這兩行代碼是遞歸過程中的關鍵步驟，它們分別獨立地計算左子樹和右子樹的高度。由于樹的高度是遞歸定義的，即樹的高度是其左子樹和右子樹高度的最大值加 1（當前節點），所以需要分別計算左右子樹的高度。

一旦得到 heightleft 和 heightright，函數就會決定：

  • 如果?heightleft?大于或等于?heightright，則當前節點的左子樹高度是決定整棵樹高度的關鍵，因此返回?heightleft + 1。
  • 如果?heightright?大于?heightleft，則右子樹的高度決定了整棵樹的高度，因此返回?heightright + 1。

這種遞歸方法確保了能夠找到從根節點到任意葉子節點的最長路徑，從而得到二叉樹的準確高度。

否則會產生棧溢出的現象

下面有一題題解，我們會進行圖解，因為一樣，所以這里不進行圖解，

先上圖

二叉樹查找值為x的節點

這里還是有點難度的

// 二叉樹查找值為x的節點
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->_data == x)return root;BTNode* ret1 = BinaryTreeFind(root->_left, x);if (ret1 != NULL){return ret1;}BTNode* ret2 = BinaryTreeFind(root->_right, x);if (ret2 != NULL){return ret2;}return NULL;}

解釋：

  1. BTNode* BinaryTreeFind(BTNode* root, BTDataType x)

    • 這是函數的聲明行，定義了一個名為?BinaryTreeFind?的函數。它接收兩個參數：一個指向?BTNode?類型的指針?root，表示二叉樹的根節點；一個?BTDataType?類型的值?x，表示要查找的值。函數返回一個指向?BTNode?類型的指針，如果找到匹配的節點，則返回該節點的地址；如果沒有找到，則返回?NULL。

  2. if (root == NULL)

    • 這行代碼檢查傳入的?root?指針是否為?NULL。如果是?NULL，表示當前節點為空，無法找到匹配的值，因此返回?NULL。

  3. if (root->_data == x)

    • 如果當前節點不為空，這行代碼比較當前節點的?_data?成員變量與給定值?x?是否相等。

  4. return root;

    • 如果找到匹配的值，即當前節點的?_data?等于?x，則返回當前節點的指針。

  5. BTNode* ret1 = BinaryTreeFind(root->_left, x);

    • 如果當前節點的值不匹配，這行代碼遞歸調用?BinaryTreeFind?函數，搜索左子樹。遞歸調用的結果（一個節點指針）被存儲在?ret1?變量中。

  6. if (ret1 != NULL)

    • 接著，檢查?ret1?是否不為空。如果不為空，表示在左子樹中找到了匹配的節點，因此返回?ret1。

  7. BTNode* ret2 = BinaryTreeFind(root->_right, x);

    • 如果左子樹中沒有找到匹配的節點，這行代碼遞歸調用?BinaryTreeFind?函數，搜索右子樹。遞歸調用的結果（一個節點指針）被存儲在?ret2?變量中。

  8. if (ret2 != NULL)

    • 然后，檢查?ret2?是否不為空。如果不為空，表示在右子樹中找到了匹配的節點，因此返回?ret2。

  9. return NULL;

    • 如果在當前節點的左子樹和右子樹中都沒有找到匹配的節點，則返回?NULL。

圖解

二叉樹第k層節點個數

// 二叉樹第k層節點個數
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL)return 0;if (k == 1)return 1;return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}

解釋：

  1. int BinaryTreeLevelKSize(BTNode* root, int k)

    • 這是函數的聲明行，定義了一個名為?BinaryTreeLevelKSize?的函數。它接收兩個參數：一個指向?BTNode?類型的指針?root，表示當前的節點（可以是任意層的節點，包括根節點）；一個整型變量?k，表示要查找的目標層級。函數返回一個整數值，表示在第?k?層上的節點總數。

  2. if (root == NULL)

    • 這行代碼檢查傳入的?root?指針是否為?NULL。如果是?NULL，表示當前節點為空，無法計算節點個數，因此返回?0。

  3. if (k == 1)

    • 這行代碼檢查目標層級?k?是否為 1。如果是 1，表示當前節點位于第 1 層，因此返回?1，表示第 1 層有一個節點。

  4. return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);

    • 如果當前節點不為空且目標層級不是第 1 層，這行代碼遞歸地調用自身兩次，分別計算左子樹和右子樹在第?k-1?層的節點個數。然后，將這兩個調用的結果相加，得到第?k?層的節點總數。

總結來說，BinaryTreeLevelKSize 函數通過遞歸的方式遍歷二叉樹，計算并返回第 k 層上的節點個數。它首先檢查當前節點是否為空，如果不為空且目標層級為第 1 層，則返回 1。如果不是第 1 層，則遞歸地計算左子樹和右子樹在降低一層后的節點個數，并將它們相加得到結果。這種方法可以正確地計算出任意二叉樹在指定層級的節點總數。

圖解

層序遍歷

什么是層序遍歷

也就是：顧名思義，一層一層的輸出

這里的關鍵點在于，怎么樣一層一層進入，輸出

那么此時我們可以采取隊列的形式來進行使用，同時進隊列，同時出隊列

所以，這里我們是直接調用隊列

隊列的講解-CSDN博客icon-default.png?t=N7T8https://blog.csdn.net/Jason_from_China/article/details/138730053

#include"Queue.h"
// 層序遍歷
void BinaryTreeLevelOrder(BTNode* root)
{// 按照順序，放入隊列里面，先進先出，后進后出的原則// 1，創建隊列，初始化// 2，如果不為空，根節點入隊列// 3，取棧頂，打印，出隊列Queue ps;QueueInit(&ps);if (root)QueuePush(&ps, root);while (!QueueEmpty(&ps)){BTNode* ret = QueueFront(&ps);QueuePop(&ps);printf("%d ", ret->_data);if (ret->_left)QueuePush(&ps, ret->_left);if (ret->_right)QueuePush(&ps, ret->_right);}//隊列的銷毀QueueDestroy(&ps);
}

解釋：

  1. #include"Queue.h"

    • 這行代碼包含了隊列數據結構的頭文件，該文件中定義了隊列操作的相關函數和數據結構。

  2. void BinaryTreeLevelOrder(BTNode* root)

    • 這是函數的聲明行，定義了一個名為?BinaryTreeLevelOrder?的函數，它接收一個指向?BTNode?類型的指針?root?作為參數，表示二叉樹的根節點。

  3. Queue ps;

    • 這行代碼聲明了一個名為?ps?的隊列變量。然而，這可能不足以正確地在某些語言中創建隊列，因為隊列可能需要動態分配（取決于其實現）。

  4. QueueInit(&ps);

    • 這行代碼調用?QueueInit?函數來初始化隊列?ps。

  5. if (root) QueuePush(&ps, root);

    • 如果根節點?root?不為空，這行代碼調用?QueuePush?函數將根節點入隊。

  6. while (!QueueEmpty(&ps))

    • 這行代碼開始一個循環，它會一直執行，直到隊列變空。QueueEmpty?函數檢查隊列是否為空。

  7. BTNode* ret = QueueFront(&ps);

    • 這行代碼調用?QueueFront?函數獲取隊列前端的節點，但不從隊列中移除它。

  8. QueuePop(&ps);

    • 這行代碼調用?QueuePop?函數從隊列中移除前端的節點。

  9. printf("%d ", ret->_data);

    • 這行代碼打印當前節點?ret?的數據。

  10. if (ret->_left) QueuePush(&ps, ret->_left);

    • 如果當前節點?ret?的左子節點存在，這行代碼將其入隊。

  11. if (ret->_right) QueuePush(&ps, ret->_right);

    • 如果當前節點?ret?的右子節點存在，這行代碼將其入隊。

  12. QueueDestroy(&ps);

    • 最后，這行代碼調用?QueueDestroy?函數銷毀隊列，釋放所有分配的內存。

總結來說，BinaryTreeLevelOrder 函數使用隊列來實現二叉樹的層序遍歷。它首先初始化一個隊列，然后將根節點入隊。在循環中，它取出隊列前端的節點，打印其數據，然后將其左右子節點（如果存在）依次入隊。這個過程一直重復，直到隊列為空。

這里的關鍵在于我們要認識到出去一個節點，進去兩個節點

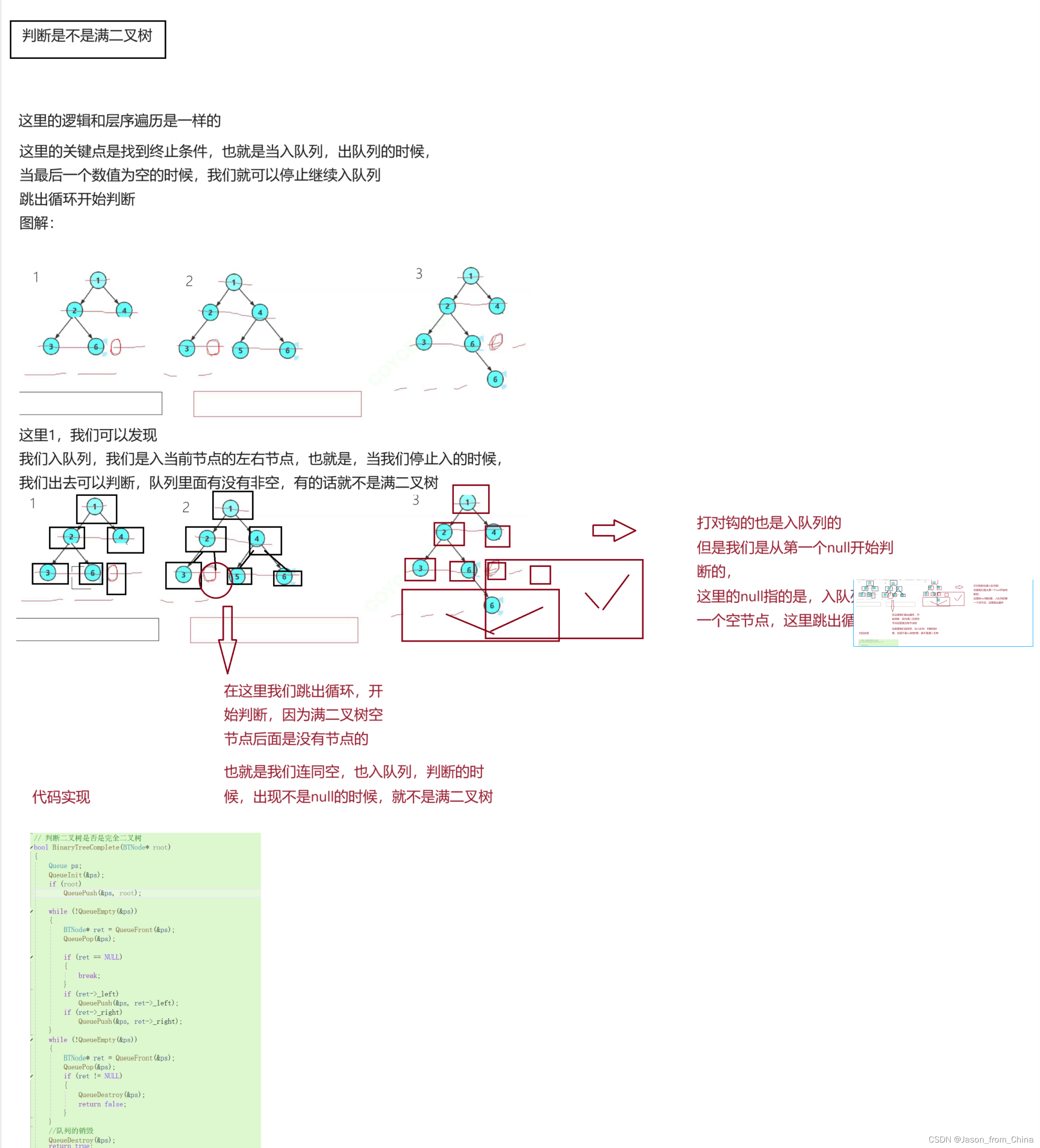
判斷二叉樹是否是完全二叉樹

這里的邏輯也是采取隊列的形式來進行判斷，只是我們需要入空，當最后入的數值為空的時候，我們需要跳出循環，然后進行判斷

// 判斷二叉樹是否是完全二叉樹
bool BinaryTreeComplete(BTNode* root)
{Queue ps;QueueInit(&ps);if (root)QueuePush(&ps, root);while (!QueueEmpty(&ps)){BTNode* ret = QueueFront(&ps);QueuePop(&ps);if (ret == NULL){break;}if (ret->_left)QueuePush(&ps, ret->_left);if (ret->_right)QueuePush(&ps, ret->_right);}while (!QueueEmpty(&ps)){BTNode* ret = QueueFront(&ps);QueuePop(&ps);if (ret != NULL){QueueDestroy(&ps);return false;}}//隊列的銷毀QueueDestroy(&ps);return true;
}

  1. #include"Queue.h"

    • 包含隊列操作的頭文件。

  2. bool BinaryTreeComplete(BTNode* root)

    • 函數聲明，返回類型為?bool，表示最終的布爾結果（是或不是完全二叉樹）。

  3. Queue ps;

    • 聲明一個隊列?ps。注意：這可能不足以在某些語言中創建隊列，因為隊列可能需要動態分配。

  4. QueueInit(&ps);

    • 初始化隊列。

  5. if (root) QueuePush(&ps, root);

    • 如果根節點不為空，則將其入隊。

  6. 第一個 while 循環：

    • 使用隊列進行層序遍歷，訪問所有節點。

  7. BTNode* ret = QueueFront(&ps);

    • 獲取隊列前端的節點。

  8. QueuePop(&ps);

    • 將隊列前端的節點出隊。

  9. if (ret == NULL) { break; }

    • 如果節點為?NULL，則退出循環。這個條件永遠不會滿足，因為?NULL?節點不會被入隊。

  10. if (ret->_left) QueuePush(&ps, ret->_left);

    • 如果存在左子節點，則將其入隊。

  11. if (ret->_right) QueuePush(&ps, ret->_right);

    • 如果存在右子節點，則將其入隊。

  12. 第二個 while 循環：

    • 這個循環的目的是檢查隊列中是否還有非?NULL?節點。

  13. BTNode* ret = QueueFront(&ps);

    • 再次獲取隊列前端的節點。

  14. QueuePop(&ps);

    • 再次將隊列前端的節點出隊。

  15. if (ret != NULL) { QueueDestroy(&ps); return false; }

    • 如果節點不為?NULL，銷毀隊列并返回?false。這部分邏輯是錯誤的，因為按照完全二叉樹的定義，隊列中應該只有?NULL?節點。

  16. QueueDestroy(&ps);

    • 銷毀隊列。

  17. return true;

    • 返回?true?表示樹是完全二叉樹。

鏈式二叉樹代碼總結

Link_Teer.h

#define _CRT_SECURE_NO_WARNINGS 1
#pragma once
#include<assert.h>
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;
//二叉樹的初始化
BTNode* BuyNode(BTDataType x);
// 二叉樹前序遍歷 
void BinaryTreePrevOrder(BTNode* root);
// 二叉樹中序遍歷
void BinaryTreeInOrder(BTNode* root);
// 二叉樹后序遍歷
void BinaryTreePostOrder(BTNode* root);
// 二叉樹節點個數
int BinaryTreeSize(BTNode* root);
// 二叉樹葉子節點個數
int BinaryTreeLeafSize(BTNode* root);
// 二叉樹高度
int BinaryTreeHeight(BTNode* root);
// 二叉樹查找值為x的節點
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉樹第k層節點個數
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉樹銷毀
void BinaryTreeDestory(BTNode* root);
// 層序遍歷
void BinaryTreeLevelOrder(BTNode* root);
// 判斷二叉樹是否是完全二叉樹
bool BinaryTreeComplete(BTNode* root);

Link_Teer.c

#include"Link_Teer.h"
//二叉樹的初始化
BTNode* BuyNode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("BinaryTreeInit:newnode:");exit(1);}newnode->_data = x;newnode->_left = NULL;newnode->_right = NULL;return newnode;
}
// 二叉樹前序遍歷 
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}
// 二叉樹中序遍歷
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}BinaryTreeInOrder(root->_left);printf("%d ", root->_data);BinaryTreeInOrder(root->_right);
}
// 二叉樹后序遍歷
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}BinaryTreePostOrder(root->_left);BinaryTreePostOrder(root->_right);printf("%d ", root->_data);
}
// 二叉樹節點個數
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}
// 二叉樹葉子節點個數
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (BinaryTreeLeafSize(root->_left) == 0 && BinaryTreeLeafSize(root->_right) == 0)return 1;return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}
// 二叉樹高度
int BinaryTreeHeight(BTNode* root)
{ if (root == NULL){return 0;}int heightleft = BinaryTreeHeight(root->_left);int heightright = BinaryTreeHeight(root->_right);return heightleft >= heightright ? heightleft + 1 : heightright + 1;
}
// 二叉樹第k層節點個數
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL)return 0;if (k == 1)return 1;return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}
// 二叉樹查找值為x的節點
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->_data == x)return root;BTNode* ret1 = BinaryTreeFind(root->_left, x);if (ret1 != NULL){return ret1;}BTNode* ret2 = BinaryTreeFind(root->_right, x);if (ret2 != NULL){return ret2;}return NULL;}
// 二叉樹銷毀
void BinaryTreeDestory(BTNode* root)
{if (root == NULL){return;}BinaryTreeDestory(root->_left);BinaryTreeDestory(root->_right);free(root);
}#include"Queue.h"
// 層序遍歷
void BinaryTreeLevelOrder(BTNode* root)
{// 按照順序，放入隊列里面，先進先出，后進后出的原則// 1，創建隊列，初始化// 2，如果不為空，根節點入隊列// 3，取棧頂，打印，出隊列Queue ps;QueueInit(&ps);if (root)QueuePush(&ps, root);while (!QueueEmpty(&ps)){BTNode* ret = QueueFront(&ps);QueuePop(&ps);printf("%d ", ret->_data);if (ret->_left)QueuePush(&ps, ret->_left);if (ret->_right)QueuePush(&ps, ret->_right);}//隊列的銷毀QueueDestroy(&ps);
}
// 判斷二叉樹是否是完全二叉樹
bool BinaryTreeComplete(BTNode* root)
{Queue ps;QueueInit(&ps);if (root)QueuePush(&ps, root);while (!QueueEmpty(&ps)){BTNode* ret = QueueFront(&ps);QueuePop(&ps);if (ret == NULL){break;}if (ret->_left)QueuePush(&ps, ret->_left);if (ret->_right)QueuePush(&ps, ret->_right);}while (!QueueEmpty(&ps)){BTNode* ret = QueueFront(&ps);QueuePop(&ps);if (ret != NULL){QueueDestroy(&ps);return false;}}//隊列的銷毀QueueDestroy(&ps);return true;
}

test.c

#include"Link_Teer.h"
//構建二叉樹
void teer()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);//BTNode* node7 = BuyNode(7);node1->_left = node2;node2->_left = node3;node1->_right = node4;node4->_left = node5;node4->_right = node6;//node2->_right = node7;printf(" 二叉樹前序遍歷測試:\n");BinaryTreePrevOrder(node1);printf("\n\n\n");printf("二叉樹中序遍歷測試:\n");BinaryTreeInOrder(node1);printf("\n\n\n");printf("二叉樹后序遍歷測試:\n");BinaryTreePostOrder(node1);printf("\n\n\n");printf("二叉樹節點個數測試:\n");int ret1 = BinaryTreeSize(node1);printf("%d", ret1);printf("\n\n\n");printf("二叉樹葉子節點個數測試:\n");int ret2 = BinaryTreeLeafSize(node1);printf("%d", ret2);printf("\n\n\n");printf("二叉樹高度測試:\n");int ret3 = BinaryTreeHeight(node1);printf("%d", ret3);printf("\n\n\n");printf("二叉樹第k層節點個數測試:\n");int ret4 = BinaryTreeLevelKSize(node1, 3);printf("%d", ret4);printf("\n\n\n");printf("二叉樹查找值為x的節點測試:\n");BTNode* ret5 = BinaryTreeFind(node1, 6);printf("%d", ret5->_data);printf("\n\n\n");printf("層序遍歷測試:\n");BinaryTreeLevelOrder(node1);printf("\n\n\n");printf("判斷二叉樹是否是完全二叉樹測試:\n");bool ret6 = BinaryTreeComplete(node1);printf("%d", ret6);}
int main()
{//構建二叉樹teer();return 0;
}

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/bicheng/17700.shtml
繁體地址，請注明出處：http://hk.pswp.cn/bicheng/17700.shtml
英文地址，請注明出處：http://en.pswp.cn/bicheng/17700.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

機器學習-7-機器學習中常用的可視化方式總結

機器學習-7-機器學習中常用的可視化方式總結

參考通透！！監督學習和無監督學習全總結！ 參考機器學習中的可視化 1 監督學習和無監督學習 監督學習和無監督學習，它們之間的主要區別在于訓練數據的標簽信息是否提供。 1.1 概述 一、監督學習(Supervised Learning)： (1)標簽信息： 監督學習使用帶有標簽的訓練數據。這…
閱讀更多...
單元測試的實現方式

單元測試的實現方式

單元測試的實現方式包括&#xff1a;人工靜態檢查、動態執行跟蹤 人工靜態檢查 人工靜態檢查是一種單元測試實現方式&#xff0c;它主要依賴開發人員的人工代碼審查和靜態分析工具來識別潛在的代碼問題。 代碼審查&#xff1a;開發人員通過仔細檢查代碼來發現潛在的問題。他…
閱讀更多...
不怕YOLOv10高歌猛進，我有YOLOv8穩扎穩打

不怕YOLOv10高歌猛進，我有YOLOv8穩扎穩打

YOLOv10 出來有幾天時間了&#xff0c;這次我沒有選擇第一時間出文章解析&#xff0c;如此頻繁的發布數字版本的 YOLO 著實讓人頭疼&#xff0c;雖然數字的更新并非舊版技術的過時&#xff0c; 但是這肯定會讓很多在校同學增加很多焦慮情緒。這里還是請大家辯證看待。 v10 這次…
閱讀更多...
解密消息隊列的復制魔法：RocketMQ vs Kafka

解密消息隊列的復制魔法：RocketMQ vs Kafka

解密消息隊列的復制魔法&#xff1a;RocketMQ vs Kafka 今天我們來聊聊一個在消息隊列世界中至關重要的主題&#xff1a;消息復制。消息復制不僅能防止消息丟失&#xff0c;還能確保系統的高可用性。即使某個節點宕機了&#xff0c;其他節點依然可以繼續工作。那么&#xff0c…
閱讀更多...
區間選點問題-貪心-C++

區間選點問題-貪心-C++

問題&#xff1a; 給定 &#x1d441; 個閉區間 [ai,bi]&#xff0c;請你在數軸上選擇盡量少的點&#xff0c;使得每個區間內至少包含一個選出的點。 輸出選擇的點的最小數量。 位于區間端點上的點也算作區間內。 輸入格式 第一行包含整數 &#x1d441;&#xff0c;表示區間數…
閱讀更多...
CSS文本粒子動畫特效之愛心粒子文字特效-Canvas

CSS文本粒子動畫特效之愛心粒子文字特效-Canvas

1. 效果圖 2.完整代碼 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><style>body,html {margin: 0;paddin…
閱讀更多...
order by工作過程和優化

order by工作過程和優化

工作過程 order by 是由優化器決定的&#xff0c;如果優化器認為filesort速度快&#xff0c;那么走filesort排序&#xff0c;如果優化器認為索引速度快&#xff0c;那么走索引排序。
閱讀更多...
有一個3x4的矩陣，求矩陣中所有元素中的最大值。要求用函數處理

有一個3x4的矩陣，求矩陣中所有元素中的最大值。要求用函數處理

解此題的算法已在之前的文章中介紹&#xff0c;詳見&#xff1a;https://mp.csdn.net/mp_blog/creation/editor/139181787 編寫程序&#xff1a; 運行結果&#xff1a;
閱讀更多...
常用的字符串方法

常用的字符串方法

length() 返回字符串的長度。 let str "HelloWorld"; console.log(str.length); // 10charAt() 返回指定位置的字符。參數&#xff1a;位置索引。 let str "HelloWorld"; console.log(str.charAt(5)); // Wconcat() 連接字符串。參數&#xff1a;一…
閱讀更多...
昵稱生成器

昵稱生成器

package mainimport ("math/rand" )// 隨機昵稱 形容詞 var nicheng_tou []string{"迷你的", "鮮艷的", "飛快的", "真實的", "清新的", "幸福的", "可耐的", "快樂的", "冷…
閱讀更多...
卷徑計算(PID輸出補償法 SCL源代碼)

卷徑計算(PID輸出補償法 SCL源代碼)

卷徑計算有很多方法，這里我們提供另一個思路，這里我們采用的是通過速度控制間接控制張力通過線速度和系統卷徑我們可以計算出我們的速度前饋量(主速度)。具體收放卷前饋量計算可以參考下面文章鏈接： 收放卷前饋量計算FC(梯形圖+SCL代碼)-CSDN博客文章瀏覽閱讀584次。這篇博…
閱讀更多...
【數據分析面試】55. 尋找雙詞組 (Python)

【數據分析面試】55. 尋找雙詞組 (Python)

題目&#xff1a; 尋找雙詞組 &#xff08;Python&#xff09; 編寫一個名為 find_bigrams 的函數&#xff0c;該函數接收一個句子或段落的字符串&#xff0c;并按順序返回其所有雙詞組的列表。 注意&#xff1a; 雙詞組是指連續的兩個單詞。 示例&#xff1a; 輸入&#x…
閱讀更多...
JavaScript（ES6）入門

JavaScript（ES6）入門

ES6 1、介紹 ECMAScript 6&#xff08;簡稱ES6&#xff09;是于2015年6月正式發布的JavaScript 語言的標準&#xff0c;正式名為ECMAScript 2015&#xff08;ES2015&#xff09;。它的目標是使得JavaScript語言可以用來編寫復雜的大型應用程序&#xff0c;成為企業級開發語言。…
閱讀更多...
Dolphinscheduler不重啟加載Oracle驅動

Dolphinscheduler不重啟加載Oracle驅動

轉載自劉茫茫看山 問題背景 某天我們的租戶反饋數據庫連接缺少必要的驅動&#xff0c;我們通過日志查看確實是缺少部分數據庫的驅動&#xff0c;因為DolphinScheduler默認只帶了Oracle和MySQL的驅動&#xff0c;并且需要將pom文件中的test模式去掉才可以在打包的時候引入。我…
閱讀更多...
Unity Dotween 定位點的制作

Unity Dotween 定位點的制作

目錄 前言 一、動畫預覽 二、動畫拆分 三、素材準備 四、曲線 OutCirc詳解 五、速度分類詳解 六、代碼 七、組件和設置 八、作者的話 前言 我答應我的粉絲接下來更新Dotween系列&#xff0c;但是我一直沒想好&#xff0c;從哪里開始講。 Dotween的安裝我就跳過了&…
閱讀更多...
QtCreator調試運行工程報錯，無法找到相關庫的的解決方案

QtCreator調試運行工程報錯，無法找到相關庫的的解決方案

最新在使用國產化平臺做qt應用開發時&#xff0c;總是遇到qtcreator內調試運行 找不到動態庫的問題&#xff0c;為什么會出現這種問題呢&#xff1f;明明編譯的時候能夠正常通過&#xff0c;運行或者調試的時候找不到相關的庫呢&#xff1f;先說結論&#xff0c;排除庫本身的問…
閱讀更多...
Flutter 中的 AnimatedList 小部件：全面指南

Flutter 中的 AnimatedList 小部件：全面指南

Flutter 中的 AnimatedList 小部件&#xff1a;全面指南 在Flutter中&#xff0c;AnimatedList是一個專門用于展示和管理一個有序列表的組件&#xff0c;它可以對列表中的項進行添加、移除和重新排序操作&#xff0c;并且這些操作都伴隨著動畫效果。這使得AnimatedList非常適合…
閱讀更多...
精釀啤酒：品質與口感在消費者選擇中的權重分析

精釀啤酒：品質與口感在消費者選擇中的權重分析

在啤酒市場中&#xff0c;消費者選擇的影響因素眾多&#xff0c;其中品質與口感是兩個核心要素。對于Fendi club啤酒而言&#xff0c;品質與口感的權重分析在消費者選擇中顯得尤為重要。 品質是消費者選擇啤酒的首要因素。隨著消費者對啤酒認知的提高&#xff0c;他們對品質的…
閱讀更多...
德邦快遞和德邦物流運費標準哪個更劃算？怎樣才能便宜的寄大件快遞？

德邦快遞和德邦物流運費標準哪個更劃算？怎樣才能便宜的寄大件快遞？

在寄大件包裹快遞時&#xff0c;我們一般都知道選擇德邦&#xff0c;那么德邦快遞和德邦物流的收費標準哪個更劃算呢&#xff1f;下面&#xff0c;讓我們一起來了解德邦快遞和德邦物流的收費標準&#xff0c;以及如何根據實際情況做出最佳選擇。 首先了解快遞費用構成 快遞費用…
閱讀更多...
Prometheus Operator創建告警規則并接入釘釘報警

Prometheus Operator創建告警規則并接入釘釘報警

prometheus之釘釘報警 前言1. 添加prometheus報警規則1.2 添加自定義報警規則文件 2. 配置釘釘報警2.2 部署dingding插件 3. 編寫alertmanager配置文件 前言 在kubenetes上安裝了kube-promethues&#xff08;包含Prometheus Operator&#xff09;,程序正常跑起來了&#xff0c…
閱讀更多...
最新文章

Copyright @ 2022~2023