?問題：

給定?𝑁?個閉區間?[ai,bi]，請你在數軸上選擇盡量少的點，使得每個區間內至少包含一個選出的點。

輸出選擇的點的最小數量。

位于區間端點上的點也算作區間內。

輸入格式

第一行包含整數?𝑁，表示區間數。

接下來?𝑁?行，每行包含兩個整數 𝑎𝑖,𝑏𝑖，表示一個區間的兩個端點。

輸出格式

輸出一個整數，表示所需的點的最小數量。

數據范圍

1≤N≤10^5,
?10^9≤𝑎𝑖≤𝑏𝑖≤10^9

輸入樣例：

3
-1 1
2 4
3 5

?代碼：

#include<iostream>
#include<algorithm>
using namespace std;
using Pii = pair<int, int>;
const int N = 100010;
Pii Range[N];
int main(){int n;cin >> n;for (int i = 0; i < n;i++){cin >> Range[i].first >> Range[i].second;}sort(Range, Range + n, [](const Pii &a, const Pii &b) -> bool{ return a.second < b.second; });int ed = -2e9, res = 0;for (int i = 0; i < n;i++){if(Range[i].first>ed){res++;ed = Range[i].second;}}cout << res << endl;
}

題解：
? ? ? ? 題意就是給你10^5以下個區間，所以我們const int N = 100010;讓你在數軸上選擇一些點，這些點要能覆蓋得到所有的區間，當然了，數量越少越好：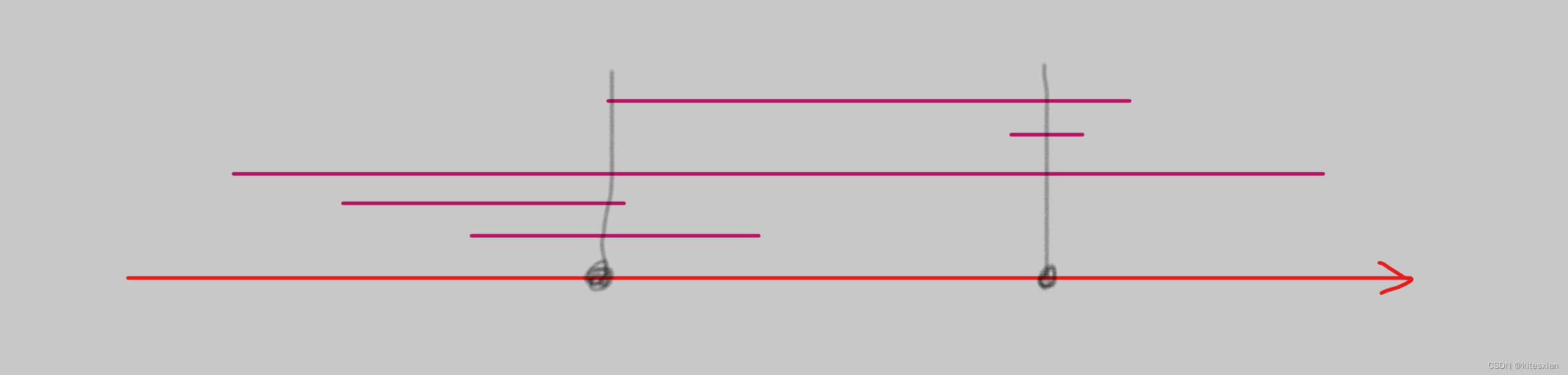

? ? ? ? 以此圖為例子，灰色筆畫的這兩個點就是答案，你再也不可能找到更少的點來覆蓋每個區間了。

? ? ? ? 計算機并不容易比我們更容易地判斷出結果，我們可以先排個序看看：
?????????我們暫且以每個區間的右端點的由小而大來排序，我們如果以每個區間的右端點來設點，其實更有可能讓這個點覆蓋到下一個區間甚至下下一個區間，這樣更可能滿足要求，這是貪心的思想，即：短視地選擇我們遍歷的區間的右端點作為答案，然后妄想讓它盡可能地覆蓋下一個、下下一個點......

? ? ? ? 我們還發現：如果A區間的右端點在下一個區間（記為B）的左端點之右的話，那么我們把A區間的右端點放到答案中，它不僅可以覆蓋A區間，連B區間都覆蓋了，甚至滿足條件它連C區間也可以給覆蓋了......我們只需維護一個變量ed記為我們剛埋的點，剛開始這個ed我們賦值為負無窮，

遇到一個區間，如果它的左端點比ed還小，那說明不用管它了，ed完全可以覆蓋它，否則，說明這一個區間我們ed夠不著，需要在這個區間設點了，即把這個區間的右端點作為新的ed，讓他去在遍歷下一個區間時，看能不能不設點，ed就能覆蓋下一個區間。

? ? ? ? 總之，遇到區間問題，盡量想到排序，貪心.....

參考鏈接：鏈接