目錄
一、二叉搜索樹的概念
二、二叉搜索樹的操作
2.1插入
2.2刪除
1.有左子樹,無右子樹
2.有右子樹,無左子樹
3.有左子樹和右子樹
三、二叉搜索樹的實現
要點
前言:為了學習map和set,需要先學二叉搜索樹作為鋪墊。
一、二叉搜索樹的概念
二叉搜索樹是一棵二叉樹,又稱為二叉排序樹,它有以下特性:
1.若左子樹不為空,則左子樹的節點值比根要小
2.若右子樹不為空,則右子樹的節點值比根要大
3.整棵樹都遵循以上規則
需要注意,二叉樹也可以是空樹。
二、二叉搜索樹的操作
2.1插入
插入的思路是,先用遞歸將樹搜索一遍,用key和樹的根的節點比大小,比它大往右走,比它小往左走,直到走到空,那么就在空的位置插入。
2.2刪除
刪除的思路比較復雜。刪除情況分三種,分別是所要刪除的節點情況,若刪除的是key節點:
1.有左子樹,無右子樹
這里就將key節點的前一個節點,指向它的后一個節點,然后釋放key節點。
2.有右子樹,無左子樹
和上面類似。
3.有左子樹和右子樹
這里比較復雜,需要將key節點與它的左子樹中的最大的一個,或者右子樹中最小的一個交換,然后再刪除key。
右子樹中最小的一個,是第一個右節點的最左的節點。若沒有最左節點,那就只能和右節點交換。
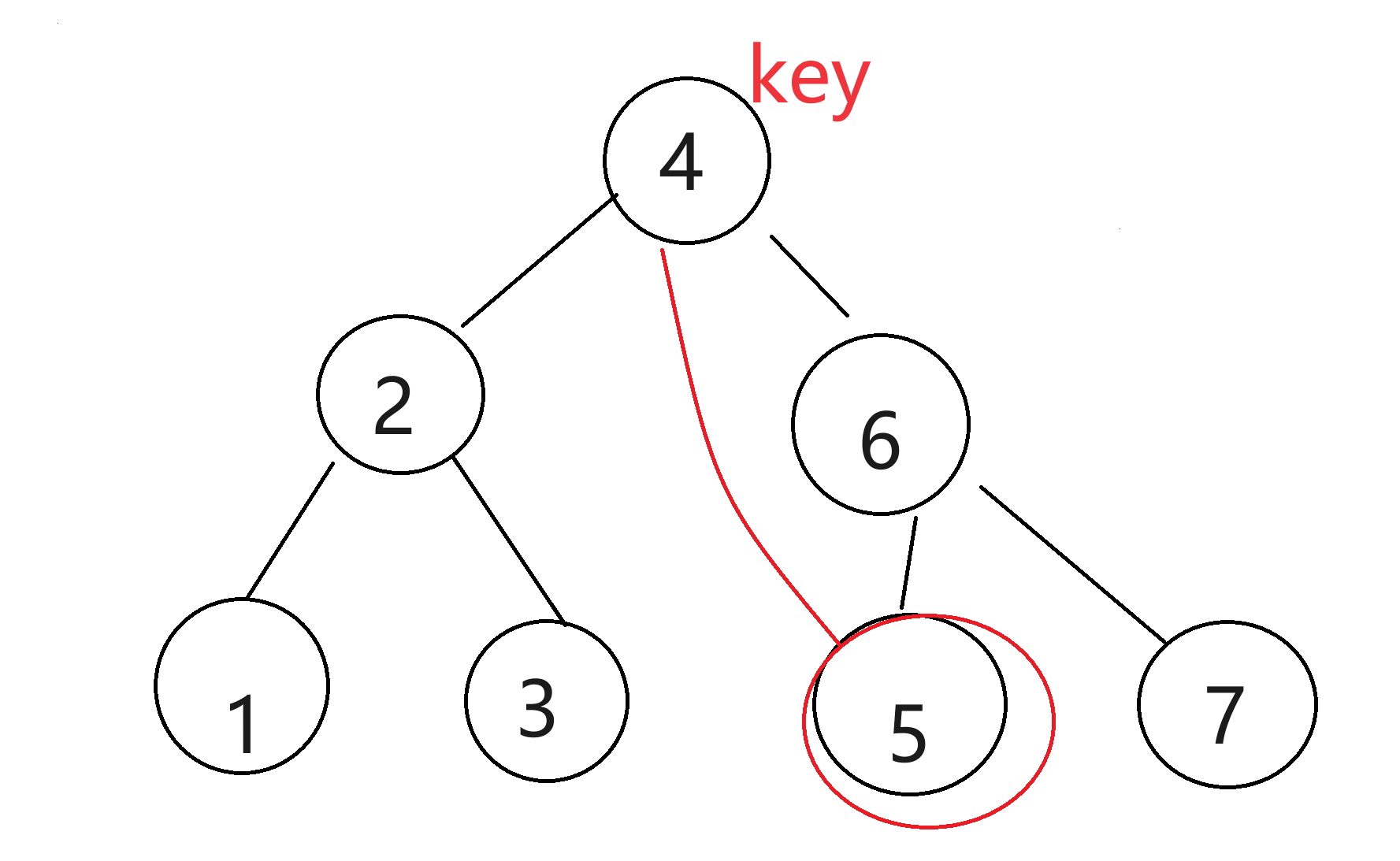
交換以后,就可以刪除key節點也就是4了。
最后一種無左子樹也無右子樹可以放在1和2中討論,歸為一種。操作比較簡單,此處不再贅述。
三、二叉搜索樹的實現
要點
1.為了體現封裝,我們只留接口放在類的public中,把具體實現的細節放在private中,這樣也方便代碼日后維護。同時由于使用遞歸,所以需要取root的引用,參數就要給root,而在類外是沒有辦法獲取作為私有的root的,因此只能把實現的細節寫在private里。
2.搜索二叉樹可以用來匹配,比如說當字典使用和門禁系統,這里可以再放入一個類模板。
3.插入的時候要新建一個節點再插入,這里會改變root的地址,所以傳引用會更好,不然就要傳二級指針了,這個很麻煩,而且在C++中是避免的。
4.刪除的時候,要先找到這個節點,再刪除。刪除時,一共涉及三個指針的操作。建議先理清思路再寫代碼。
namespace ting
{template<class K, class V>struct BSTreeNode{BSTreeNode(const K& content, const V& value):_content(content),_left(nullptr),_right(nullptr),_value(value){}K _content;BSTreeNode<K,V>* _left;BSTreeNode<K,V>* _right;V _value;};template<class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;public:bool Insert(const K& key, const V& value){return _Insert(_root, key, value);}Node* Find(const K& key){return _Find(_root, key);}bool Erase(const K& key){return _Erase(_root, key);}void InOrder(){_InOrder(_root);}private:Node* _root = nullptr;Node* _Find(Node* root, const K& key){while (root != nullptr){if (root->_content < key){root = root->_right;}else if (root->_content > key){root = root->_left;}else if (root->_content == key){return root;}}return nullptr;}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_content<<" "<<root->_value << endl;_InOrder(root->_right);}bool _Insert(Node*& root, const K& key, const V& value){if (root == nullptr){/*root->_content = key;root->_value = value;return true;*/root = new Node(key, value);//這里要給root建一個節點return true;}if (root->_content < key){return _Insert(root->_right, key, value);}else if (root->_content > key){return _Insert(root->_left, key, value);}else{return false;}}bool _Erase(Node*& root, const K& key){if (root == nullptr)return false;if (root->_content < key){return _Erase(root->_right, key);}else if (root->_content > key){return _Erase(root->_left, key);}else{Node* del = root;if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{Node* prev = root;Node* minNode = root->_right;while (minNode->_left != nullptr){prev = minNode;minNode = minNode->_left;}root->_content = minNode->_content;root->_value = minNode->_value;if (prev->_left == minNode){prev->_left = minNode->_right;}else{prev->_right = minNode->_right;}del = minNode;}delete del;return true; }}};void TestBSTree(){BSTree<string, string> dict;dict.Insert("insert", "插入");dict.Insert("erase", "刪除");dict.Insert("left", "左邊");dict.Insert("string", "字符串");string str;while (cin >> str){auto ret = dict.Find(str);if (ret){cout << str << ":" << ret->_value << endl;}else{cout << "單詞拼寫錯誤" << endl;}}string strs[] = { "蘋果", "西瓜", "蘋果", "櫻桃", "蘋果", "櫻桃", "蘋果", "櫻桃", "蘋果" };// 統計水果出現的次BSTree<string, int> countTree;for (auto str : strs){auto ret = countTree.Find(str);if (ret == NULL){countTree.Insert(str, 1);}else{ret->_value++;}}countTree.InOrder();}
}



示例)



)


)







