一、單項選擇題(每小題3分,共15分)
1. 用3個“1”和4個“0”能組成(???? )個不同的二進制數字。
?? A. 35??????? B. 36,??????? C. 37,?????? D. 38
2. 整除300的正整數的個數為(?? )。
?? A. 14 ???? B. 16 ?? C. 18???????? D. 20
3. 由6個人圍坐一周,有(???? )種坐法。
?? A. 3!,???? B. 4!,????? C. 5!, ??????D. 6!
4. 在1到350中,能被11整除的整數的個數為(???? )。
?? A.30, ?????B. 31,????? C.32,?????? D. 33
5. 邊長為1的正三角形中,放入(???? )個點,就一定能保證至少有兩個點之間的距離小于等于1/3。
A. 4,?????? B. 6,???????? C.8,??????? D. 10
二、解答題(第1小題5分,其他每小題10分,共85分)
1. 在格路模型中,求從點(0,0)出發,經過點(3,7),到達點(10,10)的格路條數? (5分)
解:格路條數為:??

2. 求不含數字3和數字8,各位數字相異且大于5400的四位數的個數.(10分)
?解:設所求的滿足題意的四位數共有N個,它們可分成如下兩類:
?(1)千位數字為5的四位數??? 因為百位數字可以是4,6,7,9類的四位數有
4·P(6,2)=120個.
?(2)千位數字大于5的四位數.因為干位數字可以是6,7,9這3個數之一,故屬于此類的四位數有
3·P(7,3)=630個
由加法原則得
?????????????? N=120十630=750.
3. 從1,2,…,30中選取3個相異的正整數,使得它們的和能被3整除,有多少種選取方法? (10分)
?解:設所求為N.以Ai(i=0、l、2)表示由集合{1,2,….30}中的除以3所得余數為i的整數所成之集,則|A0|=|A1|=|A2|=10.滿足題意的N種選取方法可分成如下兩類:
?(1)使得所選3個整數都屬于同一個Ai(i=0,1,2)的選取方法,??? 屬于此類的選取方法共有
3C(10,3)=360種.
?(2)使得所選3個整數分別屬于A0,Al,A2的選取方法,??? 屬于此類的選取方法共有
10 ×10×10=1000種.
??? 由加法原則得
???????????? N=360十l000=1360.
4.求由n(n≥2)個相異元1,2,…,n作成的1不排在第一位,2不排在第二位的全排列的個數。(10分)
解:設所求為N.因為由n(n≥2)個相異元1,2,…n作成的1不排在第一位的全排列共有(n—1) (n—1)!,其中2排在第二位的全排列有(n—2)·(n—2)!個,故
?? ?????N=(n一1)·(n—1)!一(n一2)·(n一2)!
???????? =(n2一3n十3)·(n一2)!.
5. 求從1至500的整數中能被7或11整除的整數的個數。(10分)
解:設所求為N.令S={1,2,…,500},A、B分別表示S中能被7、能被11整除的整數所成之集,則

6. 求解遞推關系:(10分)
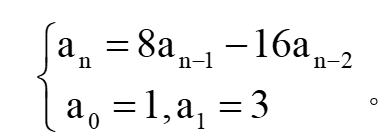
解:特征方程:
![]()
特征根:?
![]()
遞推關系的通解:
![]()
,其中C1、C2是任意常數。
將初始條件代入得:
???????????

故遞推關系的解為:
![]()
7. 利用母函數求解:若有1克砝碼3枚、2克砝碼4枚、4克砝碼2枚的砝碼各一枚,問能稱出那幾種重量?各有幾種方案?(10分)
解:所求問題對應的母函數為
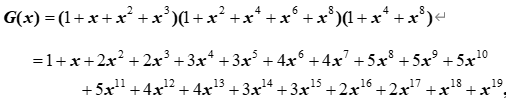
因此,能稱出的重量為0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19(克),共20種;其中稱出重量為0,1,18,19(克)的方法數各為1種,稱出重量為2,3,16,17(克)的方法數各為2種,稱出重量為4,5,14,15(克)的方法數各為3種,稱出重量為6,7,12,13(克)的方法數各為4種,稱出重量為8,9,10,11(克)的方法數各為5種。
8.將一長木條等分成7塊區域,如圖所示,請利用波利亞計數定理,求:用3種顏色給每個區域著色,不同的著色方案有多少種?(10分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
解:木條剛體運動的所有可能的置換:
??? g0=(1)(2)(3)(4)(5)(6)(7)
??? g1=(17)(26)(35)(4)
則根據波利亞計數定理,不同的著色方案數為:
???
9.在一手鐲上均勻嵌上5顆帶色的珠子,請用指數型波利亞計數定理計算恰好嵌入的是3個藍色、2個紅色珠子的不同方案數?(10分)
解:設5顆珠子依次編號為1、2、3、4、5,則手鐲剛體運動所得的置換有:
??? g0=(1)(2)(3)(4)(5),??? g1=(1)(25)(34),
??? g2=(2)(13)(45),????????? g3=(3)(24)(15),
??? g4=(4)(12)(35),????????? g5=(5)(14)(23)
??? g6=(12345),??????????????? g7=(13524),?
??? g8=(14253),???????????? g9=(15432)。
??? 那么,對應的循環指數多項式為:
![]()
其中,x3y2的系數為
![]()
也即嵌入的是3個藍色、2個紅色珠子的不同方案數是2。
(參考答案)
一、單項選擇題(每小題3分,共15分)
1.A?? 2.C??? 3.C??? 4.B??? 5.D
二、解答題(第1小題5分,其他每小題10分,共85分)
1. 在格路模型中,求從點(0,0)出發,經過點(3,7),到達點(10,10)的格路條數? (5分)
解:格路條數為:??

2. 求不含數字3和數字8,各位數字相異且大于5400的四位數的個數.(10分)
?解:設所求的滿足題意的四位數共有N個,它們可分成如下兩類:
?(1)千位數字為5的四位數??? 因為百位數字可以是4,6,7,9類的四位數有
4·P(6,2)=120個.
?(2)千位數字大于5的四位數.因為干位數字可以是6,7,9這3個數之一,故屬于此類的四位數有
3·P(7,3)=630個
由加法原則得
?????????????? N=120十630=750.
3. 從1,2,…,30中選取3個相異的正整數,使得它們的和能被3整除,有多少種選取方法? (10分)
?解:設所求為N.以Ai(i=0、l、2)表示由集合{1,2,….30}中的除以3所得余數為i的整數所成之集,則|A0|=|A1|=|A2|=10.滿足題意的N種選取方法可分成如下兩類:
?(1)使得所選3個整數都屬于同一個Ai(i=0,1,2)的選取方法,??? 屬于此類的選取方法共有
3C(10,3)=360種.
?(2)使得所選3個整數分別屬于A0,Al,A2的選取方法,??? 屬于此類的選取方法共有
10 ×10×10=1000種.
??? 由加法原則得
???????????? N=360十l000=1360.
4.求由n(n≥2)個相異元1,2,…,n作成的1不排在第一位,2不排在第二位的全排列的個數。(10分)
解:設所求為N.因為由n(n≥2)個相異元1,2,…n作成的1不排在第一位的全排列共有(n—1) (n—1)!,其中2排在第二位的全排列有(n—2)·(n—2)!個,故
?? ?????N=(n一1)·(n—1)!一(n一2)·(n一2)!
???????? =(n2一3n十3)·(n一2)!.
5. 求從1至500的整數中能被7或11整除的整數的個數。(10分)
解:設所求為N.令S={1,2,…,500},A、B分別表示S中能被7、能被11整除的整數所成之集,則

6. 求解遞推關系:(10分)
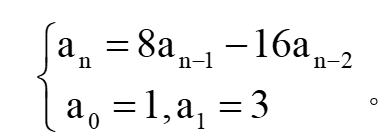
解:特征方程:
![]()
特征根:?
![]()
遞推關系的通解:
![]()
,其中C1、C2是任意常數。
將初始條件代入得:
???????????

故遞推關系的解為:
![]()
7. 利用母函數求解:若有1克砝碼3枚、2克砝碼4枚、4克砝碼2枚的砝碼各一枚,問能稱出那幾種重量?各有幾種方案?(10分)
解:所求問題對應的母函數為
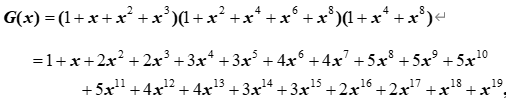
因此,能稱出的重量為0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19(克),共20種;其中稱出重量為0,1,18,19(克)的方法數各為1種,稱出重量為2,3,16,17(克)的方法數各為2種,稱出重量為4,5,14,15(克)的方法數各為3種,稱出重量為6,7,12,13(克)的方法數各為4種,稱出重量為8,9,10,11(克)的方法數各為5種。
8.將一長木條等分成7塊區域,如圖所示,請利用波利亞計數定理,求:用3種顏色給每個區域著色,不同的著色方案有多少種?(10分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
解:木條剛體運動的所有可能的置換:
??? g0=(1)(2)(3)(4)(5)(6)(7)
??? g1=(17)(26)(35)(4)
則根據波利亞計數定理,不同的著色方案數為:
???
9.在一手鐲上均勻嵌上5顆帶色的珠子,請用指數型波利亞計數定理計算恰好嵌入的是3個藍色、2個紅色珠子的不同方案數?(10分)
解:設5顆珠子依次編號為1、2、3、4、5,則手鐲剛體運動所得的置換有:
??? g0=(1)(2)(3)(4)(5),??? g1=(1)(25)(34),
??? g2=(2)(13)(45),????????? g3=(3)(24)(15),
??? g4=(4)(12)(35),????????? g5=(5)(14)(23)
??? g6=(12345),??????????????? g7=(13524),?
??? g8=(14253),???????????? g9=(15432)。
??? 那么,對應的循環指數多項式為:
![]()
其中,x3y2的系數為
![]()
也即嵌入的是3個藍色、2個紅色珠子的不同方案數是2。
)

學習筆記(二)----課程實驗環境搭建(wsl2+ubuntu+quem+xv6))
)











之擴展小部件(二十七):如何使用number_input部件?)
)


