求解最大連續子序列和問題
給定一個有n(n≥1)個整數的序列,要求求出其中最大連續子序列的和。
例如:
序列(-2,11,-4,13,-5,-2)的最大子序列和為20
序列(-6,2,4,-7,5,3,2,-1,6,-9,10,-2)的最大子序列和為16。
規定一個序列最大連續子序列和至少是0(看成0個元素構成的子序列),如果小于0,其結果為0。
1.
子數組累加和最大值問題,如何劃分問題,子數組應該如何劃分?
可以劃分為以某一個位置結尾的子數組,以i位置結尾的子數組.
所有的子數組被劃分成以0下標結尾的子數組,以1下標結尾的子數組.......
我們只需要解決每一個劃分出來的子數組集合對應的問題即可.
也就是解決以某一個位置結尾的子數組累加和最大值是多少.
2.
以i位置結尾的子數組可以劃分成兩種,第一種是只包含i位置元素,第二種是不只包含i位置元素.
只包含i位置元素的累加和最大值為arr[i],不只包含i位置元素的累加和最大值為arr[i]+(以i-1位置結尾的子數組累加和最大值).
我們要求最大值,所以以i位置結尾的子數組累加和最大值為max(arr[i],arr[i]+(以i-1位置結尾的子數組累加和最大值)).
3.
動態規劃,自底向上的動態規劃和自頂向下的動態規劃.
自底向上的動態規劃寫法
#include<bits/stdc++.h> // 導入標準庫頭文件
using namespace std; // 使用標準命名空間
#define int long long // 將int類型定義為long long類型,便于處理大數
#define endl '\n' // 將endl定義為換行符// 定義兩個測試用的數組
vector<int>arr1 = { -2,11,-4,13,-5,-2 };
vector<int>arr2 = { -6,2,4,-7,5,3,2,-1,6,-9,10,-2 };// 定義一個動態規劃數組和一個存儲當前數組的變量
vector<int>dp;
vector<int>arr;
// 定義存儲最大子數組和的變量
int ret;// 初始化函數
void init() {dp.assign(arr.size(), 0); // 將dp數組初始化為和當前數組相同大小,并賦初值為0ret = 0; // 將ret初始化為0
}// 求解最大子數組和的函數
void solve() {for (int i = 0; i < arr.size(); i++) { // 遍歷數組中的每一個元素dp[i] = max((i - 1 >= 0 ? dp[i - 1] : 0) + arr[i], arr[i]); // 計算以當前位置結尾的最大子數組和ret = max(ret, dp[i]); // 更新最大子數組和}cout << ret << endl; // 輸出結果
}// 測試函數
void f() {arr = arr1; // 將數組設置為arr1init(); // 初始化solve(); // 求解arr = arr2; // 將數組設置為arr2init(); // 初始化solve(); // 求解
}// 主函數
signed main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 提高輸入輸出效率f(); // 調用測試函數
}
自頂向下的動態規劃寫法(記憶化遞歸)
#include<bits/stdc++.h> // 導入標準庫頭文件
using namespace std; // 使用標準命名空間
#define int long long // 將int類型定義為long long類型,便于處理大數
#define endl '\n' // 將endl定義為換行符// 定義兩個測試用的數組
vector<int>arr1 = { -2,11,-4,13,-5,-2 };
vector<int>arr2 = { -6,2,4,-7,5,3,2,-1,6,-9,10,-2 };// 定義一個當前數組的變量和一個存儲最大子數組和的變量
vector<int>arr;
int ret;// 定義一個動態規劃數組
vector<int>dp;// 記憶化遞歸函數,求以位置i結尾的最大子數組和
int dfs(int i) {if (dp[i] != -1) return dp[i]; // 如果dp[i]已被計算,則直接返回dp[i]if (i - 1 < 0) { // 如果i是第一個元素dp[i] = arr[i]; // 直接返回arr[i]return dp[i]; // 返回dp[i]}dp[i] = max(dfs(i - 1) + arr[i], arr[i]); // 計算dp[i],取包含i的子數組和與僅包含i元素的子數組和的最大值ret = max(ret, dp[i]); // 更新最大子數組和return dp[i]; // 返回dp[i]
}// 初始化函數
void init() {ret = 0; // 將ret初始化為0dp.assign(arr.size(), -1); // 將dp數組初始化為和當前數組相同大小,并賦初值為-1
}// 求解最大子數組和的函數
void solve() {for (int i = 0; i < dp.size(); i++) dfs(i); // 遍歷數組中的每一個元素,調用dfs函數cout << ret << endl; // 輸出結果
}// 測試函數
void f() {arr = arr1; // 將數組設置為arr1init(); // 初始化solve(); // 求解arr = arr2; // 將數組設置為arr2init(); // 初始化solve(); // 求解
}// 主函數
signed main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 提高輸入輸出效率f(); // 調用測試函數
}
求解冪集問題
對于給定的正整數3,求1~3構成的集合的所有子集(冪集)。
| {} |
| {1} |
| {2} |
| {1,2} |
| {3} |
| {1,3} |
| {2,3} |
| {1,2,3} |
1.
組合問題,有3個整數,選出其中的部分整數作為一個集合,所有不同的情況都列出來.
對于任意的整數,在選出來的集合中,都可以選擇或者不選擇兩種方案.
所以一共有2^3種方案.對于數字1可以選擇或者不選擇,對于數字2可以選擇或者不選擇,對于數字3可以選擇或者不選擇.
一共有2*2*2=2^3種方案數.
2.
在每一種方案中對于每一個數字,都有對應的選擇,選擇或者不選擇,因此可以用1表示選擇0表示不選擇.
例如空集對應000,{1}對應100,{2}對應010,{1,2}對應110....{1,2,3}對應111.
如果000~111全部是二進制數,那么對應的十進制數是0~2^3-1.
每一個數的二進制都對應一種方案.
3.
對于每一種方案,只需要提取對于二進制數所有位置的1就知道選擇了哪些元素.
#include<bits/stdc++.h> // 導入標準庫頭文件
using namespace std; // 使用標準命名空間
#define int long long // 將int類型定義為long long類型,便于處理大數
#define endl '\n' // 將endl定義為換行符// 定義一個包含1,2,3的數組
vector<int> arr = { 1,2,3 };
// 定義一個變量n來存儲冪集的大小
int n;// 初始化函數
void init() {n = pow(2, arr.size()); // 計算冪集的大小,即2的arr.size()次冪
}// 求解冪集的函數
void solve() {for (int i = 0; i < n; i++) { // 遍歷從0到2^arr.size() - 1的所有整數cout << "{ "; // 輸出子集的左花括號for (int j = 0; j < arr.size(); j++) { // 遍歷數組中的每一個元素if (i & (1 << j)) { // 檢查整數i的第j位是否為1cout << arr[j] << " "; // 如果是,則輸出對應的數組元素}}cout << "}" << endl; // 輸出子集的右花括號和換行符}
}// 主函數
signed main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 提高輸入輸出效率init(); // 初始化solve(); // 求解冪集
}
求解0/1背包問題
有n個重量分別為{w1,w2,…,wn}的物品,它們的價值分別為{v1,v2,…,vn},給定一個容量為W的背包。設計從這些物品中選取一部分物品放入該背包的方案,每個物品要么選中要么不選中,要求選中的物品不僅能夠放到背包中,而且具有最大的價值。
并對下表所示的4個物品求出W=6時的所有解和最佳解。
| 物品編號 | 重量 | 價值 |
| 1 | 5 | 4 |
| 2 | 3 | 4 |
| 3 | 2 | 3 |
| 4 | 1 | 1 |
1.
0/1背包問題也是組合問題.有n個物品,選擇一部分物品出來放到一個集合里面.
2.
一共有4個物品,每一個物品對應一個二進制數,一共是四個位置的二進制數,0~2^4-1.
每一個數對應一種選擇方案,要么選擇要么不選擇.
一共有2^4種方案數.
3.
printf輸入格式很方便,但是要注意string轉化為c_str().
#include<bits/stdc++.h> // 導入標準庫頭文件
using namespace std; // 使用標準命名空間
#define int long long // 將int類型定義為long long類型,便于處理大數
#define endl '\n' // 將endl定義為換行符// 定義一個結構體node,用來存儲物品的重量和價值
struct node {int weight; // 物品重量int value; // 物品價值
};// 定義變量n表示物品數量,nsize表示所有可能選擇方案的數量,maxWeight表示背包的最大承重
int n = 0;
int nsize = 0;
int maxWeight = 6; // 背包最大承重為6// 定義一個包含4個物品的數組,每個物品包含重量和價值
vector<node> arr = { {5,4},{3,4},{2,3},{1,1} };// 定義一個結構體node1,用來存儲選擇方案的字符串表示、總重量和總價值
struct node1 {string str = ""; // 選擇方案的字符串表示int weight = 0; // 選擇方案的總重量int value = 0; // 選擇方案的總價值
};// 定義一個變量ret,用來存儲最佳選擇方案
node1 ret;// 初始化函數
void init() {n = 4; // 物品數量為4nsize = pow(2, n); // 所有可能選擇方案的數量為2^4=16
}// 求解0/1背包問題的函數
void solve() {cout << "0/1背包求解方案" << endl; // 輸出標題// 輸出表頭printf("%-10s%-20s%-10s%-10s%-10s\n", "序號", "選中物品", "總重量", "總價值", "能否裝入");for (int i = 0; i < nsize; i++) { // 遍歷所有可能的選擇方案node1 temp; // 定義一個臨時變量temp來存儲當前選擇方案temp.str.push_back('{'); // 添加左花括號temp.str.push_back(' ');for (int j = 0; j < n; j++) { // 遍歷所有物品if (i & (1 << j)) { // 檢查當前選擇方案是否選擇了第j個物品temp.str.push_back(j + '1'); // 如果選擇了,則將物品編號添加到字符串中temp.str.push_back(' ');temp.weight += arr[j].weight; // 將物品的重量加到總重量中temp.value += arr[j].value; // 將物品的價值加到總價值中}}temp.str.push_back('}'); // 添加右花括號// 如果當前選擇方案的總重量小于等于背包的最大承重且總價值大于當前最佳選擇方案的總價值,則更新最佳選擇方案if (temp.weight <= maxWeight && temp.value > ret.value) ret = temp;// 輸出當前選擇方案的序號、字符串表示、總重量、總價值和是否能裝入背包printf("%-10lld%-20s%-10lld%-10lld%-10s\n", i + 1, temp.str.c_str(), temp.weight, temp.value, temp.weight <= maxWeight ? "能" : "否");}// 輸出最佳選擇方案的字符串表示、總重量和總價值printf("最佳方案為 選中物品:%s,總重量:%lld,總價值:%lld", ret.str.c_str(), ret.weight, ret.value);
}// 主函數
signed main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 提高輸入輸出效率init(); // 初始化solve(); // 求解0/1背包問題
}
求解任務分配問題
有n(n≥1)個任務需要分配給n個人執行,每個任務只能分配給一個人,每個人只能執行一個任務。
第i個人執行第j個任務的成本是c[i][j](1≤i,j≤n)。求出總成本最小的分配方案。
【問題求解】所謂一種分配方案就是由第i個人執行第j個任務,用(a1,a2,…,an)表示,即第1個人執行第a1個任務,第2個人執行第a2個任務,以此類推。全部的分配方案恰好是1~n的全排列。
這里采用窮舉法求出所有的分配方案ps(全排列),再計算出每種方案的成本,比較求出最小成本的方案,即最優方案。以n=4,成本如下表所示為例討論。

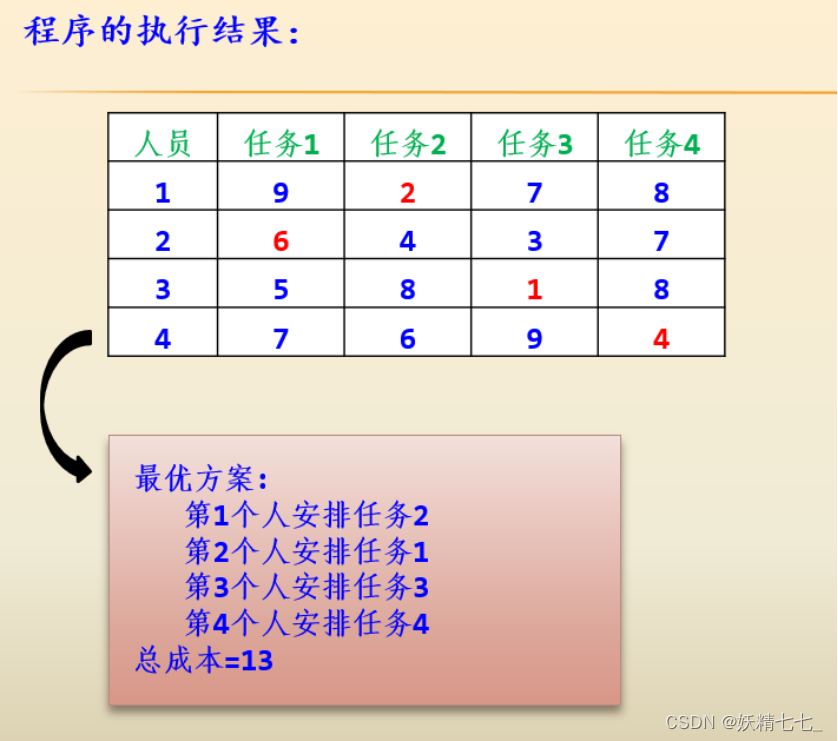
1.
排列問題,將4個任務進行全排列,列出所有的情況.
用內置函數next_premutation函數找到所有的全排序序列.
模板:
vector<int> arr = { 1,2,3,4 };do {// 輸出當前的排列for (int num : arr) {cout << num << " ";}cout << endl;} while (next_permutation(arr.begin(), arr.end()));2.
用內置函數next_premutation找到所有的全排序序列的前提是需要arr排序完畢.
//內置函數求全排序模板
#if 0#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
void init() {}
void solve() {}signed main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);init();solve();vector<int> arr = { 1,2,3,4 };do {// 輸出當前的排列for (int num : arr) {cout << num << " ";}cout << endl;} while (next_permutation(arr.begin(), arr.end()));}#endif // 1#if 1#include<bits/stdc++.h> // 導入標準庫頭文件
using namespace std; // 使用標準命名空間
#define int long long // 將int類型定義為long long類型,便于處理大數
#define endl '\n' // 將endl定義為換行符// 定義一個結構體node,用來存儲一個分配方案及其總成本
struct node {vector<int>people = { 0,0,0,0 }; // 分配方案int total = 0; // 總成本
};// 定義成本矩陣
vector<vector<int>> cost = {{9,2,7,8},{6,4,3,7},{5,8,1,8},{7,6,9,4}
};// 定義一個包含任務序號的數組
vector<int>arr = { 1,2,3,4 };
// 定義一個變量ret,用來存儲最優方案
node ret;// 初始化函數
void init() {ret.total = INT_MAX; // 將最優方案的總成本初始化為最大值
}// 求解任務分配問題的函數
void solve() {do {node temp; // 定義一個臨時變量temp來存儲當前分配方案for (int i = 0; i < arr.size(); i++) { // 遍歷所有任務temp.total += cost[i][arr[i] - 1]; // 累加當前分配方案的總成本}temp.people = arr; // 將當前分配方案賦值給temp的people字段if (ret.total > temp.total) ret = temp; // 如果當前分配方案的總成本小于最優方案的總成本,則更新最優方案} while (next_permutation(arr.begin(), arr.end())); // 生成下一個排列printf("最優方案:\n"); // 輸出最優方案for (int i = 0; i < 4; i++) { // 遍歷所有人printf("第%lld個人安排任務%lld\n", i + 1, ret.people[i]); // 輸出每個人對應的任務}printf("總成本=%lld\n", ret.total); // 輸出總成本
}// 主函數
signed main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 提高輸入輸出效率init(); // 初始化solve(); // 求解任務分配問題
}#endif // 1
結尾
最后,感謝您閱讀我的文章,希望這些內容能夠對您有所啟發和幫助。如果您有任何問題或想要分享您的觀點,請隨時在評論區留言。
同時,不要忘記訂閱我的博客以獲取更多有趣的內容。在未來的文章中,我將繼續探討這個話題的不同方面,為您呈現更多深度和見解。
謝謝您的支持,期待與您在下一篇文章中再次相遇!
)
![[處理器芯片]-6 超標量CPU實現之浮點運算](http://pic.xiahunao.cn/[處理器芯片]-6 超標量CPU實現之浮點運算)





)

)

)

排序)





