希爾排序是對插入排序的優化,如果你不了解插入排序的話,可以先閱讀這篇文章:插入排序
目錄
1.插入排序的問題
2.希爾排序的思路
3.希爾排序的實現
4.希爾排序的優化
5.希爾排序的時間復雜度
1.插入排序的問題
如果用插入排序對一個逆序有序的數組排序時,時間復雜度為O(n^2),此時效率最低。
如果用插入排序對一個順序有序的數組排序時,時間復雜度為O(n),此時效率最高。
我們發現,被排序的對象越接近有序,插入排序的效率越高,這時希爾就有了一個想法:如果可以將數組變得接近有序后再用插入排序呢?
2.希爾排序的思路
希爾排序是對插入排序的優化,它的思路是先選定一個整數作為增量,這里我們以gap(間隔)表示,將間隔為gap的數據分為一組,這樣就可以分出gap組以gap為公差的等差數列的數據組。之后將這些數據組排序(把每組數據排序),之后將gap縮小,繼續分組并進行排序,重復上述動作,直到gap縮小至1,此時排完了之后剛好有序。
為了讓數組更接近有序的排序稱為預排序,而最后一次排序是直接插入排序,而由于前面的操作使數據變得接近有序,因此最后一次直接插入排序需要移動的數據很少,效率便很高了。
下面我們來實現希爾排序。
現在我們給定如下數組,并以3為gap,可將數組根據顏色分為3組以3為公差的等差數列。
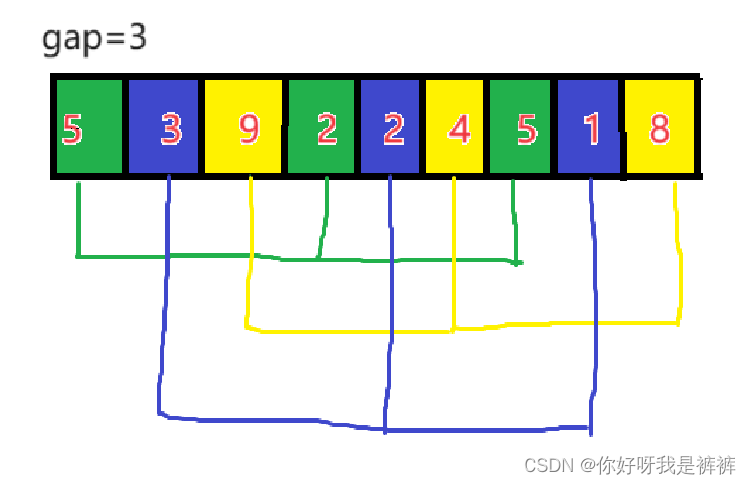
之后我們對這三組數據進行插入排序
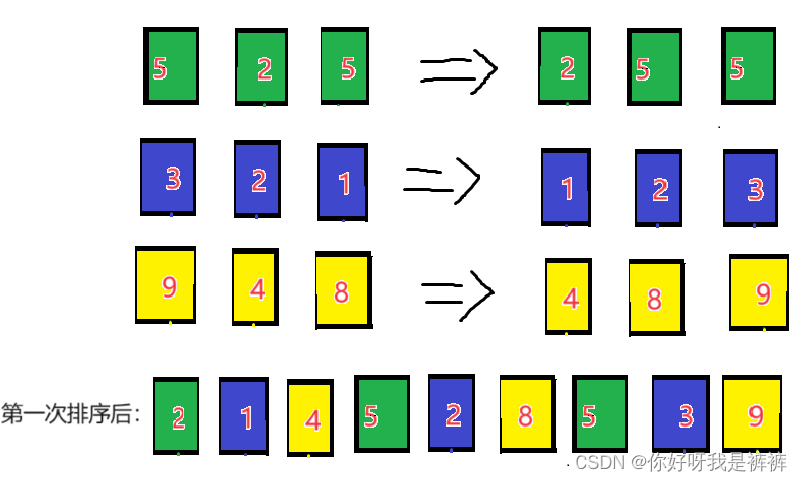
之后我們將間隔縮小, 以2為間隔,我們就可以分出兩組以2為公差的等差數列。
這里也并不一定要只減少1,減少多少看我們想減少多少。

現在我們完成第二次排序

現在我們的數組已經非常接近有序,我們最后再以1為間隔,得到一組以1為間隔的等差數列,再完成最后一次排序,也就是直接插入排序,即可使得我們的數組有序。
3.希爾排序的實現
現在我們根據我們的思路來逐步實現希爾排序
第一步:以3為間隔,排序第一組綠色的

在已經學習了插入排序的基礎上,我們來實現一下排序綠色
//代碼中的n代表數組長度,后面的代碼不再解釋。
int gap = 3;
//n-gap后的數據為最后一組數據,而當i等于我們的前一組數據時
//排序的就是最后一組數據,因此結束條件為i<n-gap
for (int i = 0; i < n - gap; i += gap)
{int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;
}第二步:進行第一次排序??
由于我們先前已經實現了排序綠色的,而排序藍色的和排序黃色的不過是起始位置不同,因此我們再嵌套一層循環即可。
for (int j = 0; i < gap; j++)
{int gap = 3;//n-gap后的數據為最后一組數據,而當i等于我們的前一組數據時//排序的就是最后一組數據,因此結束條件為i<n-gapfor (int i = j; i < n - gap; i += gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}
}現在我們已經完成了第一次排序,那么后面的排序我們控制gap即可
for (int gap = 3; gap > 0; gap--)
{for (int j = 0; i < gap; j++){for (int i = j; i < n - gap; i += gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}這時我們發現我們的代碼達到了驚人的四層循環...這段代碼未免有些過于恐怖...
那我們有沒有什么辦法優化這段代碼呢??
4.希爾排序的優化
這時有一位大佬給出了這么一個解決方法:
我們不再一次比較一個數據組,
而是先比較第一個數據組的第一個數據和第二個數據,
然后比較第二個數據組的第一個數據和第二個數據,
之后比較第三個數據組的第一個數據和第二個數據,
然后比較第二個數據組的第二個數據和第三個數據,
這么一直比較下去,就可以完成我們第一次預排序的效果。
如下圖所示,相同顏色的線表示比較的數據。

代碼如下所示:?
int gap = 3
for (int i = 0; i < n - gap; i++)
{int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;
}現在我們已經完成了第一趟的排序,接下來我們控制gap即可。
int gap = 3;
while (gap > 0)
{for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}gap--;
}現在這段代碼看起來就舒服多了。但是我們的gap就一定每次都減1嗎?
我們之前說過,預排序是為了讓數組更加有序,我們只要能夠讓數組更加有序就可以了,沒有必要每次讓gap減1,gap太大了反而會有一些副作用。
這時有一位大佬寫了這么一個希爾排序:?
int gap = n;
while (gap > 0)
{gap /= 2;for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}
}這里的第一趟循環以二分之數組長度為間隔,后續的循環每次都除以2。
到了最后一次循環之時,gap要么等于2,要么等于3;而它們除2都等于1。這樣就保證了最后一次循環是直接插入排序,可謂是相當完美了。
現在我們將其封裝在函數體內,完成最終版的希爾排序
void InsertSort(int* a, int n)
{int gap = n;while (gap > 0){gap /= 2;for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}5.希爾排序的時間復雜度
我們發現我們最終版的希爾排序也擁有三層循環,于是乎我們大家就對希爾排序的效率產生了疑問.但是利用我們現有數學能力無法計算出希爾排序的時間復雜度,只能給出一個大致范圍
下面給出嚴蔚敏教授數據結構書中的相關論述:

在這里也可以給大家大概畫一下圖,由于每次排序都會對后續的排序產生影響,因此我們后續的排序移動的數據會越來越少,因此效率還是比較高的。?
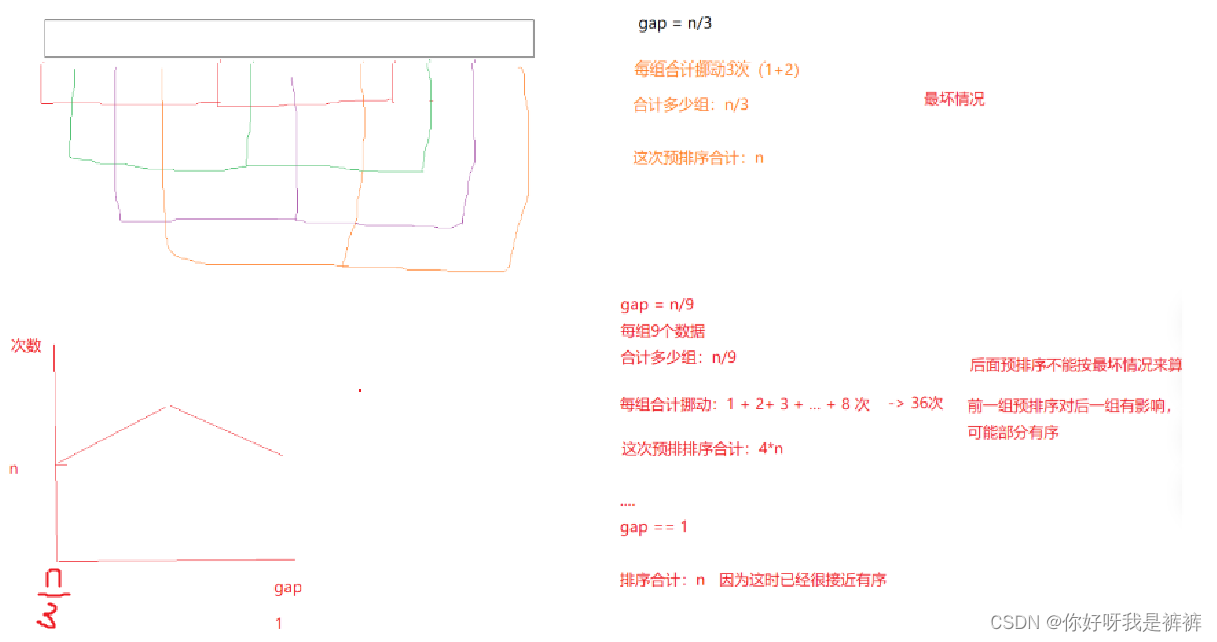


)

)
)


】繼承)




)


容器(4)ApplicationContextAware)


