這是一個關于偏序集的定理，事實上它也可以擴展到圖論，dp等中，是一個很有意思的東西

偏序集

偏序集是由集合$S$以及其上的一個偏序關系$R$定義的，記為$(S,R)$

偏序關系：

對于一個二元關系$R?S\times S$,如果其滿足：

• $?x\in S,xRx$ 自反性
• $?x,y\in S$,若$xRy$且$yRx$,則$x=y$ 反對稱性
• $xRy,yRz\to xRz$ 傳遞性
  顯然自然數集$N$以及最常見的小于等于關系$\le$,$(N,\le )$就構成了一個偏序集
  事實上$(N^{?},|)$也是一個偏序集，其中$|$表示正整數的整除關系

以下為了討論方便，我們將$R$簡記為$\le$,當然它可以指代小于等于關系之外的其它關系

此外，$?x,y\in S$,如果$x\le y$或$y\le x$，那么我們就說它們是可比的，否則說它們是不可比的

定義完了偏序集，我們可以從圖上來看看它具體的樣子

哈斯圖(Hasse 圖)

考慮一個偏序集$(S,\le )$,$?x,y\in S$,如果$x\le y$且不存在$zS.T.x\le z\le y$,我們稱為$y$覆蓋$x$,那么此時我們就連一條從$x$指向$y$的有向邊，最后得到的圖就稱為這個偏序集$(S,\le )$的Hasse圖

比如下圖是$x,y,z$的冪集關于包含關系得到的Hasse圖

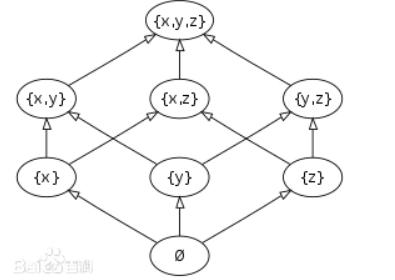
由于偏序關系滿足了反對稱性，所以Hasse圖里面一定沒有自環（否則就會合并成一個點），所以我們可以說Hasse圖一定是一張DAG

其它偏序集的前置芝士

還是記我們要討論的偏序集為$(S,\le )$

鏈：
偏序集中的一個全序子集。形式化地說，若集合$C?S$,且$?a,b\in C$,$a,b$是可比的，那么$C$就是$S$的一個鏈
鏈這個名字起的就很有水平，因為我們不難發現，偏序集中的一個全序子集，其在Hasse圖中似乎就一定表現為一條鏈。比如上圖中的 { { x , y , z } , { x , z } , { x } , { ? } } \{\{x,y,z\},\{x,z\},\{x\},\{\phi\}\} {{x,y,z},{x,z},{x},{?}}就是一個全序子集，在圖中剛好也表現成一條鏈。但我沒有嚴格證明，這邊擱置。
類似地，我們定義一個反鏈
反鏈：
若集合$C?S$,且$?a,b\in C$,$a,b$是不可比的，那么$C$就是$S$的一個反鏈
在圖上看的話， { { x } , { y } , { z } } \{\{x\},\{y\},\{z\}\} {{x},{y},{z}}就是一個反鏈

深度:
最長鏈大小

寬度：
最長反鏈大小

以上兩個定義也是相當的形象。因為我們不難發現，如果把Hasse圖按照偏序關系從低到高排列的話，鏈在圖中往往就是一條豎著的，而反鏈是橫著的，由此給出如上定義

最小鏈劃分：
將集合$S$劃分為最少的若干個不相交的鏈

最小反鏈劃分：
將集合$S$劃分為最少的若干個不相交的反鏈

Dilworth 定理

現在可以給出Dilworth 定理的具體內容了

Lemma1 對于任意有限偏序集，其最長反鏈大小必等于最小鏈劃分中鏈的數目
其對偶形式也成立：
Lemma2 對于任意有限偏序集，其最長鏈大小必等于其最小反鏈劃分中反鏈的數目

以下討論均假定偏序集有限

總結以下：
最小鏈劃分 = 最長反鏈大小 = 偏序集寬度
最小反鏈劃分 = 最長鏈大小 = 偏序集深度

先來證Lemma2：

記定理中的最長鏈大小為n，我們對n做數學歸納法
顯然n=1時定理成立
若n=k時定理成立，我們來證 n=k+1時定理成立
此時偏序集中的最長鏈長度為k+1,我們取出集合$S$的所有極大元，組成集合$M$,顯然$M$是一個反鏈，并且考慮$S?M$,其最大鏈長一定為k（因為取出了所有的極大元），根據之前的歸納假設，$S?M$的最小反鏈劃分數目為 k，再加上M自己是一個反鏈，從而此時S的最小反鏈劃分數為 k+1 = 最長鏈長度 $\square$

再來看Lemma1：

考慮偏序集$(S,\le )$,記$|S|=m$，我們對m進行歸納
$m=1$時Lemma1顯然成立
若$m=k$時定理成立，我們來證$m=k+1$時定理成立:

設$A$是集合$S$的一條最長反鏈，記為
A = { a 1 , a 2 , . . . a w } A = \{a_1,a_2,...a_w\} A={a1?,a2?,...aw?}
其中$|A|=w$
我們取
D ( A ) = { x ? A ∣ ? α ∈ S , x ≤ a } D(A) = \{x\notin A|\exists \alpha \in S,x\leq a\} D(A)={x∈/A∣?α∈S,x≤a}
U ( A ) = { x ? A ∣ ? α ∈ S , a ≤ x } U(A) = \{x\notin A|\exists \alpha \in S,a\leq x\} U(A)={x∈/A∣?α∈S,a≤x}
顯然$D(A)?U(A)?A=S$

若存在最長反鏈$A$使得$D(A),U(A)$均非空：
$A$是$S$的最長反鏈，故$A$也是$A?D(A)$的一個最長反鏈。注意到$|U(A)|\ge 1$,故$|A?D(A)|\le k$，從而由歸納假設，$A?U(A)$可以劃分為$w$條鏈$c_1,c_2,...c_w$，其中$c_i$的極大元是$a_i$.(這一點顯然)
同理，$A?D(A)$也可以劃分為$w$條鏈$d_1,d_2,...d_w$,其中$d_i$的極小元是$a_i$
從而，我們就可以將$S$劃分為$w$條鏈：$c_1\cup d_1,....c_w\cup d_w$

若對于任意最長反鏈$A$,都有$D(A)=?$或$U(A)=?$
由假設，任一條反鏈$A$必定構成全上界或者全下界。在$S$中選一個極大元$y$,再選一個極小元$x$滿足$x\le y$, { x , y } \{x,y\} {x,y}構成一條鏈$C$,從而在集合$S?C$中，任一條最長反鏈的大小為$w?1$（必定去除了一個元素），從而根據歸納假設，$S?C$的最小鏈劃分數為$w?1$,再加上$C$自己是一條鏈，故$S$的最小鏈劃分數為$w$

$\square$

應用舉例

求一個序列的最大非遞增序列長度以及其最少可以劃分為多少個非遞增序列

考慮由(位置，元素大小)這個二元組組成的集合，再定義一個偏序關系$<$:
$a<b$當且僅當 $a$的位置<$b$的位置且$a$的值$<b$的值

從而這就構成了一個偏序集$(s,<)$,并且要求的分別就是集合的最長反鏈以及最小反鏈劃分數
第一個問題可以直接dp即可，第二個問題，根據Dilworth 定理，實際上就是求偏序集的最長鏈大小，實際上也就是序列的LIS，非常妙的一個轉化。

與DAG

之前說過，Hasse圖就是一個DAG，而反過來，我們將DAG的點作為集合$S$的元素，將偏序關系$\le$定義為點之間的可達性，就定義了一個偏序集$(S,\le )$
從而DAG上的最小可重路徑覆蓋（要求覆蓋所有點）就等價于偏序集$(S,\le )$上的最小鏈覆蓋

同理，將DAG上的有向邊作為集合$T$的元素，將偏序關系${\le }^{\prime }$定義為邊之間的可達性，就得到的另一個偏序集$(T,{\le }^{\prime })$
從而DAG上的最小可重路徑覆蓋(要求覆蓋所有邊)就等價于偏序集$(T,{\le }^{\prime })$上的最小鏈覆蓋

Erd?s–Szekeres 定理

含至少$rs+1$個元素的實數序列 { a } \{a\} {a}要么有一個長為$r+1$的不下降子序列，要么有一個長為$s+1$?的不上升子序列
Proof:
設序列長度為$n\ge rs+1$,定義偏序集$\{(i,a_i){\}}_{i=1}^n$,其上的偏序關系$\le$定義為：
$$(i,a_i)\le (j,a_i)?(i\le j\wedge a_i\le a_j)$$
假設該偏序集的寬度$\le s$,則由Dilllworth定理可知其最小鏈覆蓋數$\le s$,若這些鏈的長度都$\le r$,則總元素數$\le rs<rs+1\le n$
矛盾。
$\square$