ARIMA模型在河流水質預測中的應用_含代碼

#水質模型 #時間序列 #python應用

ARIMA 時間序列模型簡介

時間序列是研究數據隨時間變化而變化的一種算法，是一種預測性分析算法。它的基本出發點就是事物發展都有連續性，按照它本身固有的規律進行。ARIMA(p,d,q)模型全稱為差分自回歸移動平均模型 (Autoregressive Integrated Moving Average Model,簡記 ARIMA). 是比較成熟且簡單的時間預測模型之一。其中 AR 為自回歸, I 為差分, MA 為移動平均。
趨勢參數：

  • p：趨勢自回歸階數。
  • d：趨勢差分階數。
  • q：趨勢移動平均階數。

差分

差分（difference）又名差分函數或差分運算，差分的結果反映了離散量之間的一種變化，是研究離散數學的一種工具。它將原函數f(x) 映射到f(x+a)-f(x+b) 。差分運算，相應于微分運算，是微積分中重要的一個概念。總而言之，差分對應離散，微分對應連續。差分又分為前向差分、向后差分及中心差分三種。
通常情況下我們用到的是前向差分公式如下：
xk=x0+kh,(k=0,1,…,n)
△f(xk)=f(xk+1)?f(xk)
差分的階
稱為階的差分，即前向階差分 ，如果數學運用根據數學歸納法，有其中，為二項式系數。特別的，有前向差分有時候也稱作數列的二項式變換

在高錳酸鹽指數序列預測可行性的說明

通過觀察水質變化趨勢，高錳酸鹽指數波動不劇烈，存在明顯的中心波動規律。

python實現

環境準備

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
import pymysqlwarnings.filterwarnings("ignore")  
# 忽略警告，不然一大堆警告，多是python及對應包升高導致，不影響使用
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
from matplotlib.pylab import style  # 自定義圖表風格
style.use('ggplot')# 解決中文亂碼問題
plt.rcParams['font.sans-serif'] = ['Simhei']
# 解決坐標軸刻度負號亂碼
plt.rcParams['axes.unicode_minus'] = False# pip install statsmodelsfrom statsmodels.graphics.tsaplots import plot_acf, plot_pacf  # 自相關圖、偏自相關圖
from statsmodels.tsa.stattools import adfuller as ADF  # 平穩性檢驗
from statsmodels.stats.diagnostic import acorr_ljungbox  # 白噪聲檢驗
import statsmodels.api as sm  # D-W檢驗,一階自相關檢驗
from statsmodels.graphics.api import qqplot  # 畫QQ圖,檢驗一組數據是否服從正態分布
from statsmodels.tsa.arima.model import ARIMA

連接數據

通過數據庫，excel 都可以，列名為監測時間、設備名稱、設備因子、監測值。

def conn_sql():conn = pymysql.connect(host=" ",port= ,user=" ",password=" ",db=" ",charset="utf8")sql = ""read_sql = pd.read_sql(sql, conn)return read_sql
read_sql=conn_sql()

數據處理

def nseri(s,y ):aidunqiao = read_sql.loc[read_sql['設備名稱'] == s, :]ai_cod = aidunqiao.loc[read_sql['監測因子'] == y, :]ai_cod_mn = ai_cod.loc[:, ["監測時間", '監測值']]baseline = ai_cod.loc[:, ["監測時間", '監測值']]ai_cod_mn.set_index('監測時間', inplace=True)interp_cod_mn = ai_cod_mn["監測值"].interpolate()ai_cod_mn["cod"] = interp_cod_mnstarttime = baseline.iloc[0, 0]rows = baseline.shape[0]endtime = baseline.iloc[rows - 1, 0]year_month_day = pd.date_range(starttime, endtime, freq="h").strftime("%Y%m%d%h%m%s")a_ser = pd.DataFrame({'監測時間': year_month_day})a_ser.set_index('監測時間', inplace=True)df = pd.concat([a_ser, ai_cod_mn], axis=0, join="outer")df = df.reset_index(drop=False)df['監測時間'] = pd.to_datetime(df['監測時間'])df1 = df.drop_duplicates(subset="監測時間", keep="last", ignore_index=True)df2 = df1.sort_values(by="監測時間", ignore_index=True)df2["cod"] = df2["監測值"].interpolate()df2.drop(columns="監測值", inplace=True)df2.set_index('監測時間', inplace=True)return df2

主要是 將數據生成無空連續的逐小時 時間序列數據 插值方法為線性插值

數據解讀

查看acf
df2 = df2.dropna()
# 解決有nan的問題
plot_acf(df2,lags=50).show()

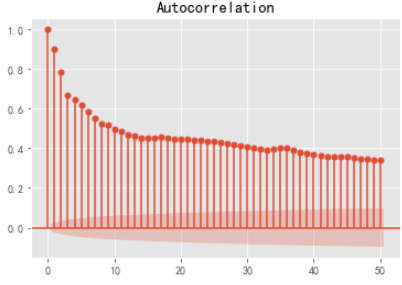
解讀 拖尾為p 。基本大于0.5 現在和未來有很強的相關性

單位根檢驗
print('原始序列的ADF檢驗結果為：',ADF(df2.cod))

原始序列的ADF檢驗結果為： (-7.19465930048855, 2.452407467867345e-10, 37, 9199, {‘1%’: -3.431061069214289, ‘5%’: -2.8618542472812902, ‘10%’: -2.5669372687639176}, 11281.50483165621)

解讀：P值小于顯著性水平α（0.05），不接受原假設（非平穩序列），說明原始序列是平穩序列。

白噪聲檢驗
print('一階差分序列的白噪聲檢驗結果為：',acorr_ljungbox(df2,lags=1,return_df =bool))

一階差分序列的白噪聲檢驗結果為： lb_stat lb_pvalue 1 7467.631465 0.0

p值為0小于0.05，不是白噪聲

綜上可以采用 arima 模型

定階 人工識圖
#一階差分，我們不需要這么做，看下代碼怎么寫的。
df2_mn=df2.diff(periods=1, axis=0).dropna()
#自相關圖
plot_acf(df2,lags=20).show()
#解讀：拖尾 有長期相關性 p 取1 
#偏自相關圖 
plot_pacf(df2,lags=20).show()
#偏自相關圖
plot_pacf(df2,lags=50).show()
#解讀：自相關圖，0階拖尾；偏自相關圖，截尾。則ARIMA(p,d,q)=ARIMA(1,0,n)

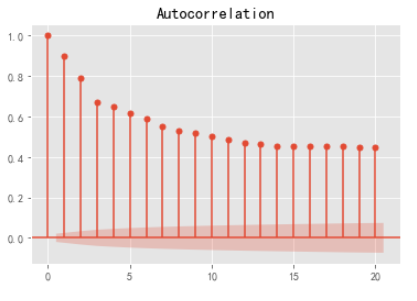
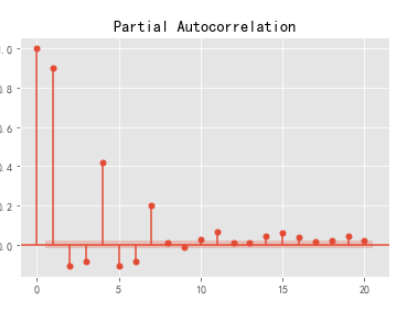
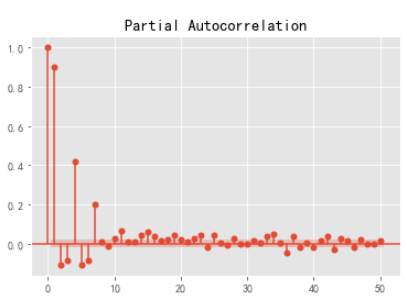
參數調優

AIC調優

from statsmodels.tsa.arima.model import ARIMA
aic_matrix=[]
for p in range(5):tmp=[]for q in range(5):try:tmp.append(ARIMA(df2,order=(p,0,q)).fit().aic)except:tmp.append(None)aic_matrix.append(tmp)
aic_matrix# p,q=aic_matrix.stack().idxmin() #最小值的索引
# 手動查找最小值 同樣為1，0，4

也可以用BIC調優 不再贅述

模型建立

model = ARIMA(df2, order=(1, 0, 4))
result_arima = model.fit()

模型預測

定義畫圖函數

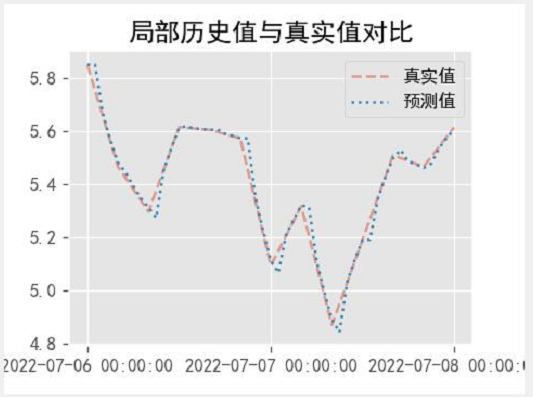
def pic1(result_arima,df2):t1 = "2022/7/6 00:00:00"t2 = "2022/7/8 00:00:00"predict_more=result_arima.predict(t1 ,t2 )t = pd.date_range(t1, t2 , freq="h").strftime("%y%m%d%h%m%s")new_ticks = pd.date_range(t1, t2 , freq="d").strftime("%y%m%d%h%m%s")axc.clear()axc.set_title("局部歷史值與真實值對比")axc.plot(t,df2[t1 :t2],linestyle = "--",alpha=0.5)axc.plot(t,predict_more,linestyle = ":")axc.legend(['真實值','預測值'])axc.set_xticks(new_ticks)   # 創建畫布控件canvas = FigureCanvasTkAgg(fig1, master=root)  # A tk.DrawingArea.canvas.draw()canvas.get_tk_widget().place(x=63,y=200)


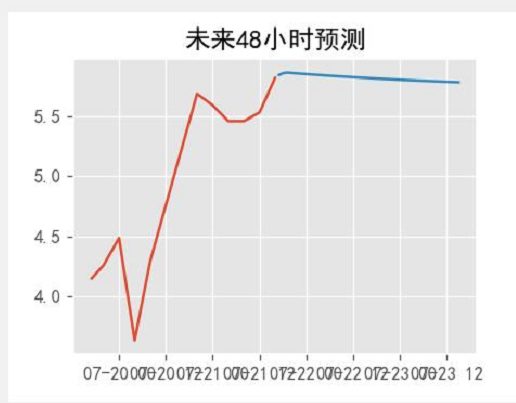
def fore_picture(result_arima,df2):df3 = df2.reset_index(drop=False)rows = df3.shape[0]endtime = df3.iloc[rows - 1, 0]forecast = pd.Series(result_arima.forecast(48), index=pd.date_range(endtime, periods=48, freq='H'))df_last = df2.iloc[-48:]    data = pd.concat((df_last, forecast), axis=0)data.columns = ['監測值濃度', '未來48小時']axc2.clear()axc2.set_title("未來48小時預測")axc2.plot(data) # 創建畫布控件canvas = FigureCanvasTkAgg(fig2, master=root)  # A tk.DrawingArea.canvas.draw()canvas.get_tk_widget().place(x=600,y=200)


def compare2(result_arima,df2):df3 = df2.reset_index(drop=False)rows = df3.shape[0]endtime = df3.iloc[rows - 1, 0]starttime = df3.iloc[0, 0]predict=result_arima.predict(starttime , endtime)axc3.clear()axc3.set_title("全部預測值真實值對比")axc3.plot(df2.index,df2['cod'],linestyle = "--",alpha=0.5)axc3.plot(df2.index,predict,linestyle = ":")axc3.legend(['真實值','預測值'])canvas = FigureCanvasTkAgg(fig3, master=root)  # A tk.DrawingArea.canvas.draw()canvas.get_tk_widget().place(x=1200,y=200)

模型可視化及GUI初探

用Tkinter 實現自動選擇站點及因子

# 副本
from tkinter.ttk import *
from  tkinter import *
import matplotlib
matplotlib.use('TkAgg')
from matplotlib.backends.backend_tkagg import FigureCanvasTkAgg
from matplotlib.figure import Figureroot = Tk()
root.title("ARIMA預測模型")
root.geometry("1800x900+50+50")  # 長x寬+x*ylb1 = Label(root,text='站點選擇',fg='black', font=('微軟雅黑',15),  height=2,  relief=FLAT)
lb2 = Label(root,text='因子選擇',fg='black', font=('微軟雅黑',15),  height=2,  relief=FLAT)
lb3 = Label(root,text='預測結果（48h）',fg='black', font=('微軟雅黑',15),  height=2,  relief=FLAT)
# lb4 = Label(root,text='歷史預測對比',fg='black', font=('微軟雅黑',15),  height=2,  relief=FLAT)# lb5 = Label(root,text=comb1.get(),fg='black', font=('微軟雅黑',15),  height=2,  relief=FLAT)
lb1.place(x=63,y=20)
lb2.place(x=300,y=20)
lb3.place(x=63,y=110)
# lb4.place(x=510,y=110)
# lb5.place(x=820,y=110)
var1 = StringVar()
comb1= Combobox(root,textvariable=var1,values = site)
comb1.place(x=63,y=80)
var2 = StringVar()
comb2= Combobox(root,textvariable=var2,values=factor)
comb2.place(x=300,y=80)def select_device(event):s = comb1.get()print(s)return sdef select_factor (event):y = comb2.get()print(y)return ycomb1.bind("<<ComboboxSelected>>", select_device)
comb2.bind("<<ComboboxSelected>>", select_factor)def click(event):s = comb1.get()y = comb2.get()df2 = nseri(s,y )model = ARIMA(df2, order=(1, 0, 4))result_arima = model.fit()fig1 = Figure(figsize=(4, 3), dpi=120)axc = fig1.add_subplot(111)axc.clear()pic1(result_arima,df2)fig2 = Figure(figsize=(4, 3), dpi=120)axc2 = fig2.add_subplot(111)axc2.clear()fore_picture(result_arima,df2)fig3 = Figure(figsize=(4, 3), dpi=120)axc3 = fig3.add_subplot(111)axc3.clear()compare2(result_arima,df2)    but1 = Button(root, text='計算',font=('微軟雅黑',15),  height=1)
but1.place(x=300,y=110)  but1.bind("<Button-1>",click)root.mainloop()

結果預覽
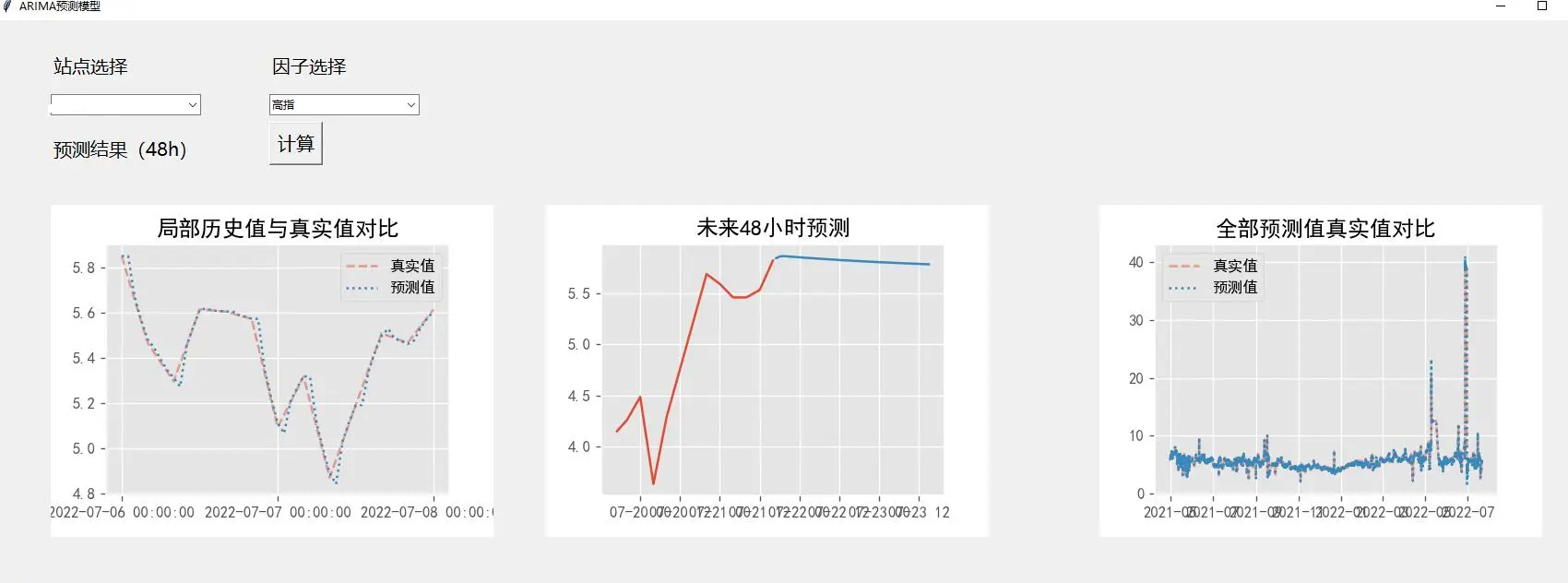
111.png

模型評價

模型評價方法： 濃度準確率， 等級準確率

濃度準確率

等級準確率：實測的類別與預測的類別相同時，則視為預測正確，預測正確的個數占預測的總個數的百分比，即為模型預測準確率。指標預測準確率的詳細計算方法如下式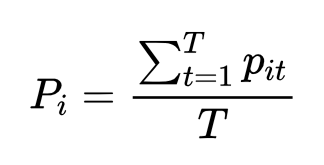：image.png

Pi為類別相對誤差，T 為驗證期內實測值的時間點數，t為實測值與預測值對應的時刻，pit為實測的類別與模擬的類別相比值，如果類別相同則為1，否則為0。

結果提取

def format1(df2):df7=pd.Series()for i in range(180) :df3= df2[:-4*(1+i)]        model = ARIMA(df3, order=(1, 0, 4))result_arima1 = model.fit()df4 = df3.reset_index(drop=False)rows = df4.shape[0]endtime = df4.iloc[rows - 1, 0]forecast = pd.Series(result_arima1.forecast(5), index=pd.date_range(endtime, periods=5, freq='H'))df8 = forecast.tail(1)    df7 = pd.concat((df7,df8),axis=0,join='inner')return df7 
f2 =format1(df2)
f2.to_excel("forceful.xls")

結果分析

時間原因用的excel 分析

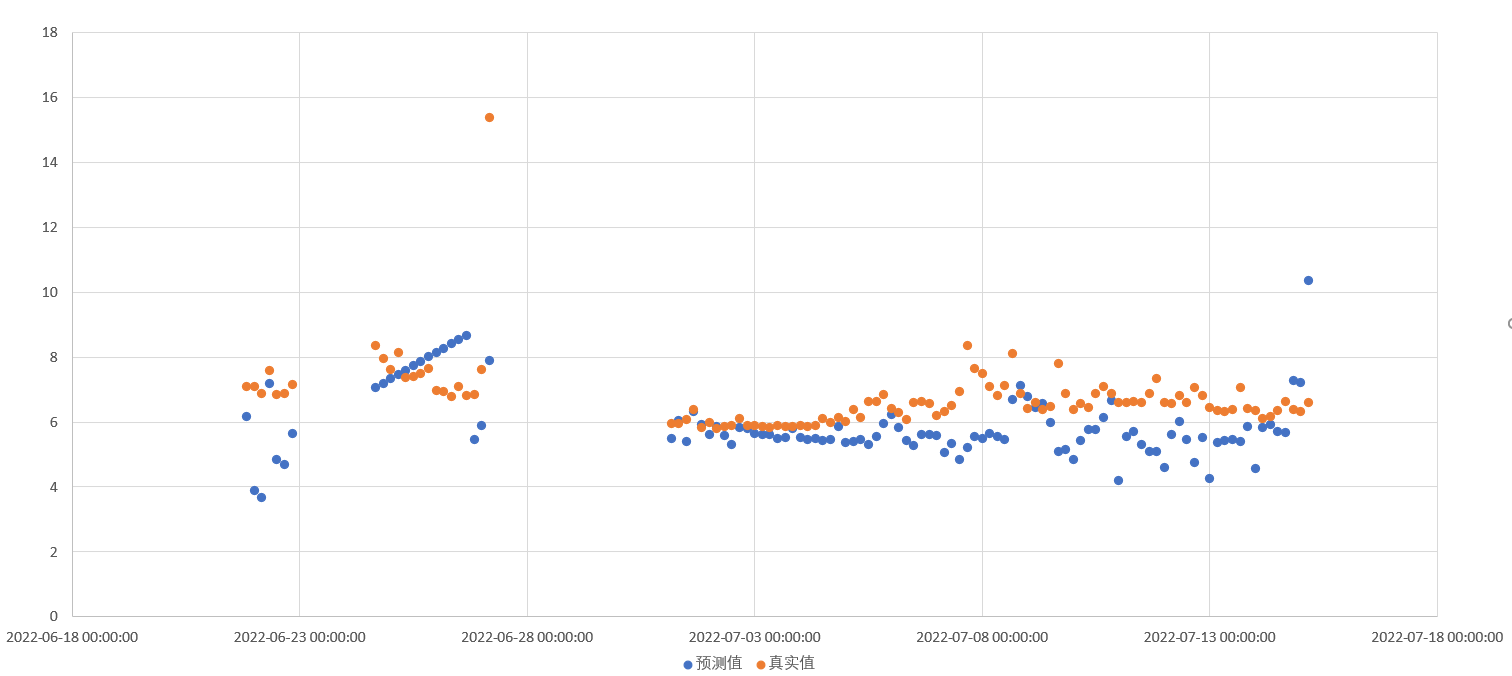
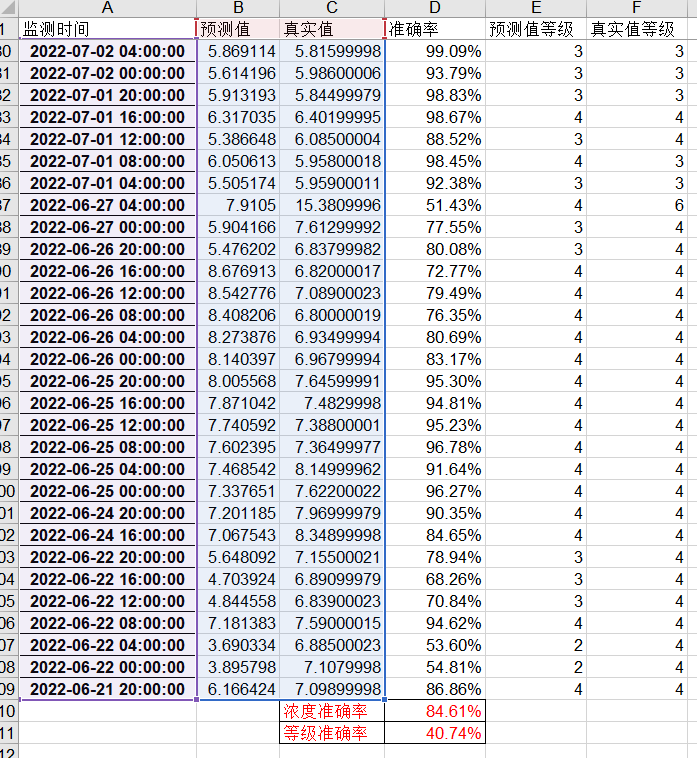
對比了6月21日~2022/7/15 高指真實值與預測值的結果，濃度預測準確率為84.61%，等級準確率40.74%，等級準確率偏低的原因為實際監測結果在6附近波動，為Ⅲ類水質標準。
預測對比時間窗口存在降雨，實際結果有一定波動，濃度預測準確率能到達84.6%，有一定的推廣價值。

ARIMA .summary() 解讀

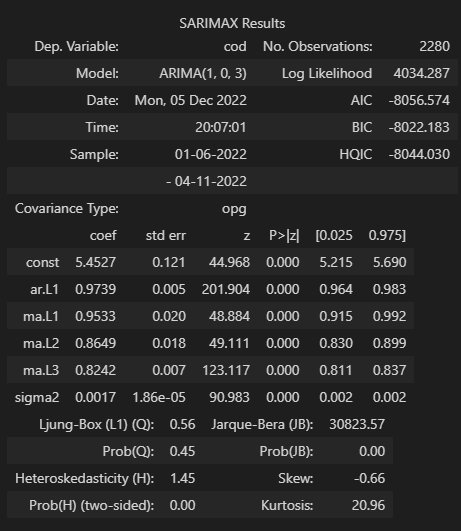
  1. 左上 為模型基本信息，Dep. Variable（需要預測的變量）、Model（模型及其參數）、Date、Time、Sample（樣本數據）、No. Observations（觀測數據的數量）
  2. 右上 Log Likelihood（對數似然函數）標識最適合采樣數據的分布。雖然它很有用，但AIC和BIC會懲罰模型的復雜性，這有助于使我們的ARIMA模型變得簡潔。赤池的信息準則（AIC）有助于確定線性回歸模型的強度。AIC 會懲罰添加參數的模型，因為添加更多參數將始終增加最大似然值。貝葉斯信息準則（BIC）與 AIC 一樣，BIC 也會懲罰模型的復雜性，但它也包含數據中的行數。Hannan-Quinn信息標準（HQIC），與AIC和BIC一樣是模型選擇的另一個標準；但是它在實踐中并不常用。AIC 、BIC 越小越好
  3. 中部 確保模型中的每個項在統計意義上是否顯著。若p值大于0.05，則項不顯著。
  4. 下部：Ljung-Box（modified Box-Pierce test）測試錯誤是白噪音 Ljung-Box (L1) (Q) 為Lag1的LBQ檢驗統計量，其Prob(Q)為 0.01，p值為0.94。由于p值高于0.05，因此我們不能拒絕零假設（誤差是白噪音）

討論與總結

  1. ARIMA 模型在高錳酸鹽指數上的預測效果超過80%,經過初步研究，適用于水質在線站點。
  2. 模型可用于單站點單因子預測，不需要其他參數，約束小，預測精度高。
  3. 模型對波動劇烈的因子，預測效果不好，不適用于所有因子，所有站點。
  4. 對于新的數據集需要做平穩性檢驗，白噪聲檢驗。
  5. 需要采用數據人工識圖+自動的方式實現定階，選擇最優的 p，d，q。
  6. 可以繼續在 ARIMAX（多元時間序列模型）等方面深入研究。
    感謝看到最后，
    最后打個廣告，我新開了微信公眾號（環境貓 er），這也是我在公眾號發布的第一篇文章，我會堅持發布 python 環境業務解決方案，python 辦公自動化，GIS 作圖經驗，學習筆記，辦公技巧，工具分享等內容。
    堅持 Bulid in public ，希望與你一起加油，一同成長。
    qrcode_for_gh_b2ae4cd1414a_258.jpg

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/web/9868.shtml
繁體地址，請注明出處：http://hk.pswp.cn/web/9868.shtml
英文地址，請注明出處：http://en.pswp.cn/web/9868.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

SSH文件傳輸

SSH文件傳輸

一、設置SSH密鑰對&#xff0c;實現記住密碼 要避免每次使用scp或ssh時都輸入密碼&#xff0c;你可以設置SSH密鑰對&#xff08;一對公鑰和私鑰&#xff09;&#xff0c;并將公鑰添加到遠程服務器上。這樣&#xff0c;你的系統可以通過密鑰自動驗證身份&#xff0c;而無需手動…
閱讀更多...
Blazor入門-基礎知識+vs2022自帶例程的理解

Blazor入門-基礎知識+vs2022自帶例程的理解

參考&#xff1a; Blazor 教程 - 生成首個應用 https://dotnet.microsoft.com/zh-cn/learn/aspnet/blazor-tutorial/intro Blazor基礎知識&#xff1a;Visual Studio 2022 中的Blazor開發入門_vs2022 blazor webassembly-CSDN博客 https://blog.csdn.net/mzl87/article/detail…
閱讀更多...
NSSCTF | [SWPUCTF 2021 新生賽]jicao

NSSCTF | [SWPUCTF 2021 新生賽]jicao

打開題目&#xff0c;發現高亮顯示了一個 php 腳本 這是腳本的內容 <?php highlight_file(index.php); include("flag.php"); $id$_POST[id]; $jsonjson_decode($_GET[json],true); if ($id"wllmNB"&&$json[x]"wllm") {echo $flag;…
閱讀更多...
idea中數據庫的連接（保姆級）

idea中數據庫的連接（保姆級）

點擊idea中的database 然后再點擊加號 創建 然后選擇第一欄data source 再選擇mysql 然后選擇數據庫的連接方式 再輸入密碼 這里我們本來就是localhost所有就不用改 選擇端口號 然后點擊Test Connection 測試連接 第一次連接會下載連接的文件 我們只需要 等待它下載完成就好了 …
閱讀更多...
文本批量操作指南：文本合并技巧，批量處理大量文本的方法

文本批量操作指南：文本合并技巧，批量處理大量文本的方法

在數字化時代&#xff0c;文本處理成為我們日常生活和工作中不可或缺的一部分。無論是整理文檔、數據分析還是內容創作&#xff0c;我們都需要處理大量的文本數據。為了提升工作效率&#xff0c;掌握文本批量操作和合并的技巧變得尤為重要。本文將為您提供一份詳細的文本批量操…
閱讀更多...
機器學習算法應用——CART決策樹

機器學習算法應用——CART決策樹

CART決策樹&#xff08;4-2&#xff09; CART&#xff08;Classification and Regression Trees&#xff09;決策樹是一種常用的機器學習算法&#xff0c;它既可以用于分類問題&#xff0c;也可以用于回歸問題。CART決策樹的主要原理是通過遞歸地將數據集劃分為兩個子集來構建決…
閱讀更多...
力扣 256. 粉刷房子 LCR 091. 粉刷房子 python AC

力扣 256. 粉刷房子 LCR 091. 粉刷房子 python AC

動態規劃 class Solution:def minCost(self, costs):row, col len(costs), 3dp [[0] * col for _ in range(row 1)]for i in range(1, row 1):for j in range(col):dp[i][j] costs[i - 1][j - 1]if j 0:dp[i][j] min(dp[i - 1][1], dp[i - 1][2])elif j 1:dp[i][j] m…
閱讀更多...
【QT教程】QT6硬件高級編程實戰案例 QT硬件高級編程

【QT教程】QT6硬件高級編程實戰案例 QT硬件高級編程

QT6硬件高級編程實戰案例 使用AI技術輔助生成 QT界面美化視頻課程 QT性能優化視頻課程 QT原理與源碼分析視頻課程 QT QML C擴展開發視頻課程 免費QT視頻課程 您可以看免費1000個QT技術視頻 免費QT視頻課程 QT統計圖和QT數據可視化視頻免費看 免費QT視頻課程 QT性能優化視頻免…
閱讀更多...
【GoLang基礎】通道（channel）是什么？

【GoLang基礎】通道（channel）是什么？

問題引出&#xff1a; Go語言中的通道&#xff08;channel&#xff09;是什么&#xff1f; 解答&#xff1a; 通道&#xff08;channel&#xff09;是 Go 語言中用于協程&#xff08;goroutine&#xff09;之間通信和同步的機制。通道提供了一種安全、簡單且高效的方式&#x…
閱讀更多...
idea運行SpringBoot項目爆紅提示出現：Java HotSpot(TM) 64-Bit Server VM warning...讓我來看看~

idea運行SpringBoot項目爆紅提示出現：Java HotSpot(TM) 64-Bit Server VM warning...讓我來看看~

在運行SpringBoot項目的時候&#xff0c;發現總有這個警告提示出現&#xff0c;有點強迫癥真的每次運行項目都很難受啊&#xff01;那么今天便來解決這個問題&#xff01; 先來看一下提示內容&#xff1a;Java HotSpot(TM) 64-Bit Server VM warning: Options -Xverify:none an…
閱讀更多...
FreeRTOS標準庫例程代碼

FreeRTOS標準庫例程代碼

1.設備STM32F103C8T6 2.工程模板 單片機: 部分單片機的程序例程 - Gitee.comhttps://gitee.com/lovefoolnotme/singlechip/tree/master/STM32_FREERTOS/1.%E5%B7%A5%E7%A8%8B%E6%A8%A1%E6%9D%BF 3.代碼 1-FreeRTOS移植模板 #include "system.h" #include "…
閱讀更多...
C語言編程中布爾設置位掩碼示例

C語言編程中布爾設置位掩碼示例

在C語言編程中&#xff0c;當你想使用整數&#xff08;通常是unsigned int或uint8_t, uint16_t, uint32_t等&#xff09;的位來存儲多個布爾設置時&#xff0c;你會使用位掩碼。每個設置對應于整數中的一個位&#xff0c;你可以通過位操作&#xff08;如按位與&、按位或|、…
閱讀更多...
Rust：用 Warp 庫實現 Restful API 的簡單示例

Rust：用 Warp 庫實現 Restful API 的簡單示例

直接上代碼&#xff1a; 1、源文件 Cargo.toml [package] name "xcalc" version "0.1.0" edition "2021"# See more keys and their definitions at https://doc.rust-lang.org/cargo/reference/manifest.html[dependencies] warp "…
閱讀更多...
uniap之微信公眾號支付

uniap之微信公眾號支付

近來用uniapp開發H5的時候&#xff0c;需要接入支付&#xff0c;原來都是基于后端框架來做的&#xff0c;所以可謂是一路坑中過&#xff0c;今天整理下大致流程分享給大家。 先封裝util.js&#xff0c;便于后面調用 const isWechat function(){return String(navigator.userA…
閱讀更多...
隊列的實現（使用C語言）

隊列的實現（使用C語言）

完整代碼鏈接&#xff1a;DataStructure: 基本數據結構的實現。 (gitee.com) 目錄 一、隊列的概念&#xff1a; 二、隊列的實現&#xff1a; 使用鏈表實現隊列&#xff1a; 1.結構體設計&#xff1a; 2.初始化&#xff1a; 3.銷毀&#xff1a; 4.入隊&#xff1a; 5.…
閱讀更多...
OC foudation框架（下）的學習

OC foudation框架（下）的學習

OCfoudation框架&#xff08;下&#xff09; 前面學習了有關OCfoudation框架的部分內容&#xff0c;我們現在對于后面的內容繼續學習。 文章目錄 OCfoudation框架&#xff08;下&#xff09;數組&#xff08;NSArray和NSMutableArray&#xff09;對集合元素整體調用方法排序使用…
閱讀更多...
會賺錢的人都在做這件事：你了解嗎？

會賺錢的人都在做這件事：你了解嗎？

在我們日常生活的點滴中&#xff0c;以及在各種場合的交互中&#xff0c;利他思維始終扮演著不可或缺的角色。當我們追求合作與共贏時&#xff0c;單方面的自我立場顯然是不夠的&#xff0c;真正的關鍵在于換位思考&#xff0c;尋找并滿足對方的需求。 互利互贏的核心理念正是利…
閱讀更多...
設置docker容器時區

設置docker容器時區

設置docker容器時區 查看當前系統時間 1.1 查看當前系統版本 cat /etc/issue1.2 查看當前系統時間 date查看鏡像默認時間 2.1 alpine鏡像 sudo docker run -it --rm alpine date2.2 ubuntu鏡像 sudo docker run -it --rm ubuntu date2.3 centos鏡像 sudo docker run -it --rm …
閱讀更多...
虛擬知識付費系統源碼推薦,在線教育雙十一怎么做活動？

虛擬知識付費系統源碼推薦,在線教育雙十一怎么做活動？

又是一年光棍節&#xff0c;啊不是&#xff0c;剁手節。小伙伴們早就摩拳擦掌準備剁手了&#xff0c;這個時候&#xff0c;幾乎所有線上平臺都行動起來了&#xff0c;而在線教育行業也沒有閑著。如今&#xff0c;雙十一已經成為了各大在線教育公司用來變現的一個大殺器&#xf…
閱讀更多...
ruoyi-vue-pro 使用記錄（4）

ruoyi-vue-pro 使用記錄（4）

ruoyi-vue-pro 使用記錄&#xff08;4&#xff09; CRM數據庫線索客戶商機合同回款產品其他 CRM 文檔 主要分為 6 個核心模塊&#xff1a;線索、客戶、商機、合同、回款、產品。 線索管理以 crm_clue 作為核心表客戶管理以 crm_customer 作為核心表商機管理以 crm_business 作…
閱讀更多...
最新文章

Copyright @ 2022~2023