目錄
?編輯1）隊列的介紹
核心操作
3）隊列的鏈表實現和數組實現
使用數組實現隊列
2）棧的介紹
核心操作
4）棧的數組實現
使用語言內置的實現
使用數組手動實現棧
5）環形隊列的實現 leecode622
代碼解析
視頻鏈接
【算法講解013【入門】隊列和棧-鏈表、數組實現】
1）隊列的介紹
先進先出。進了從尾進，從頭出。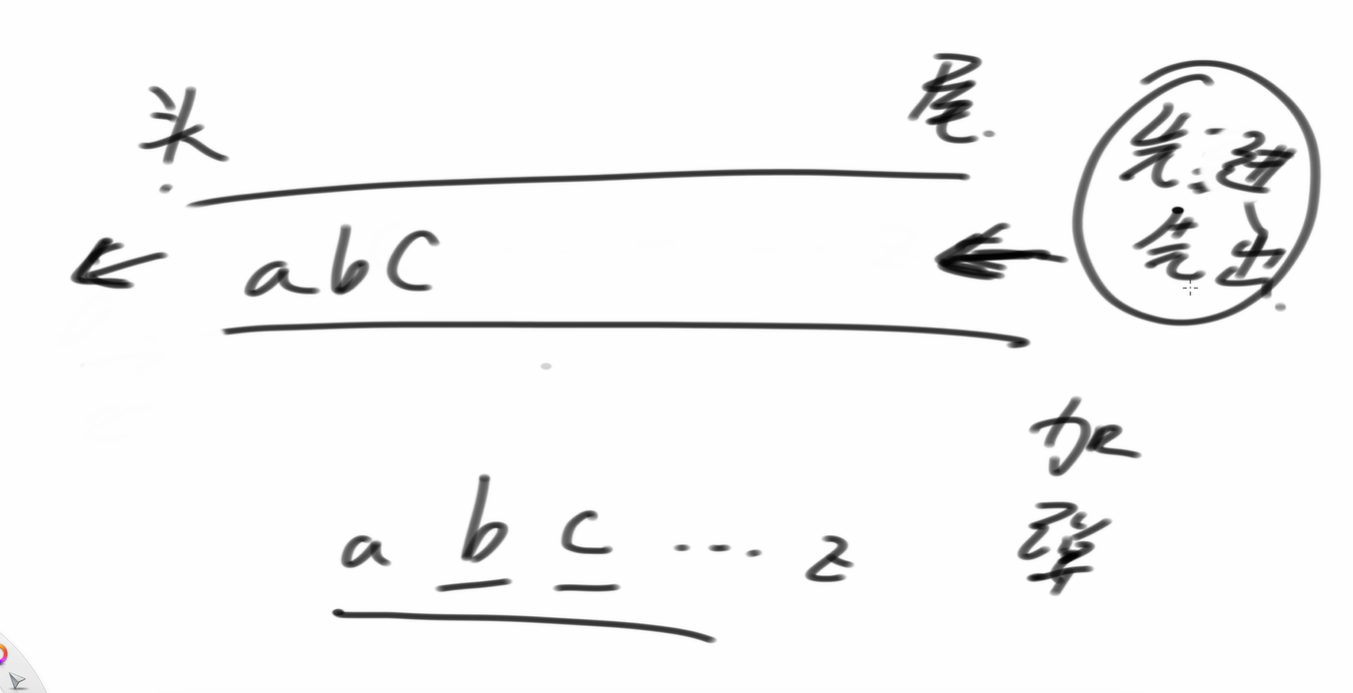
隊列我們認為范圍是左閉右開的。范圍是[L，R），因此如果L<R,就說明有元素，如果L==R，說明隊列里沒有元素。
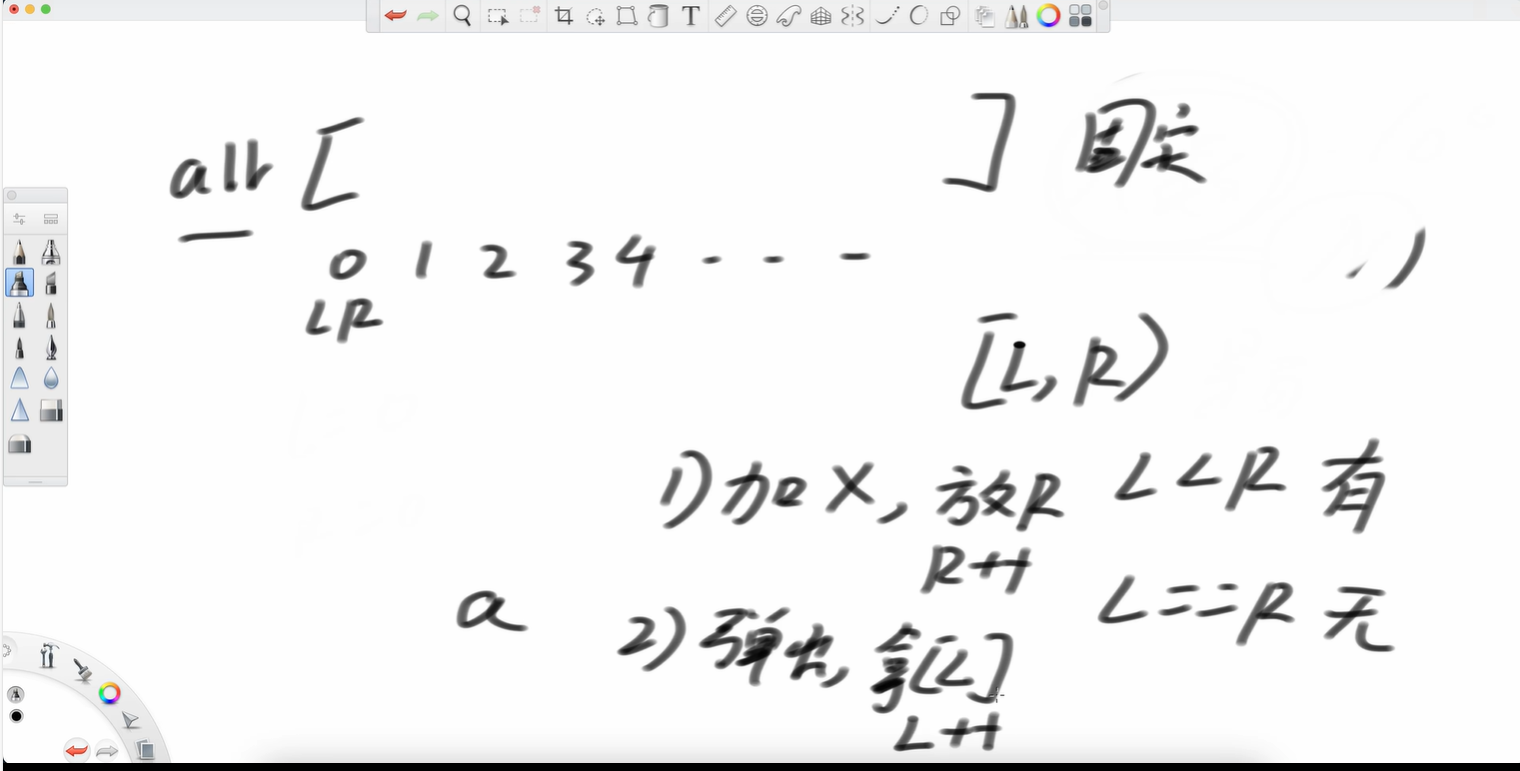
如果我們想加b到R位置，那么我們R++；（原來R在1位置）
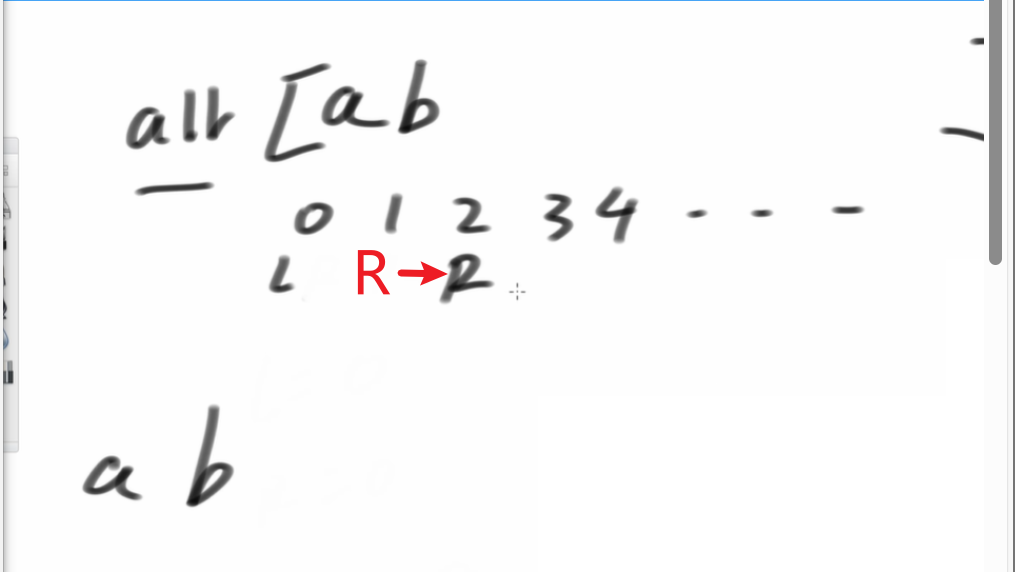
如果我們想讓數彈出，那么我們拿L位置的數，讓L++
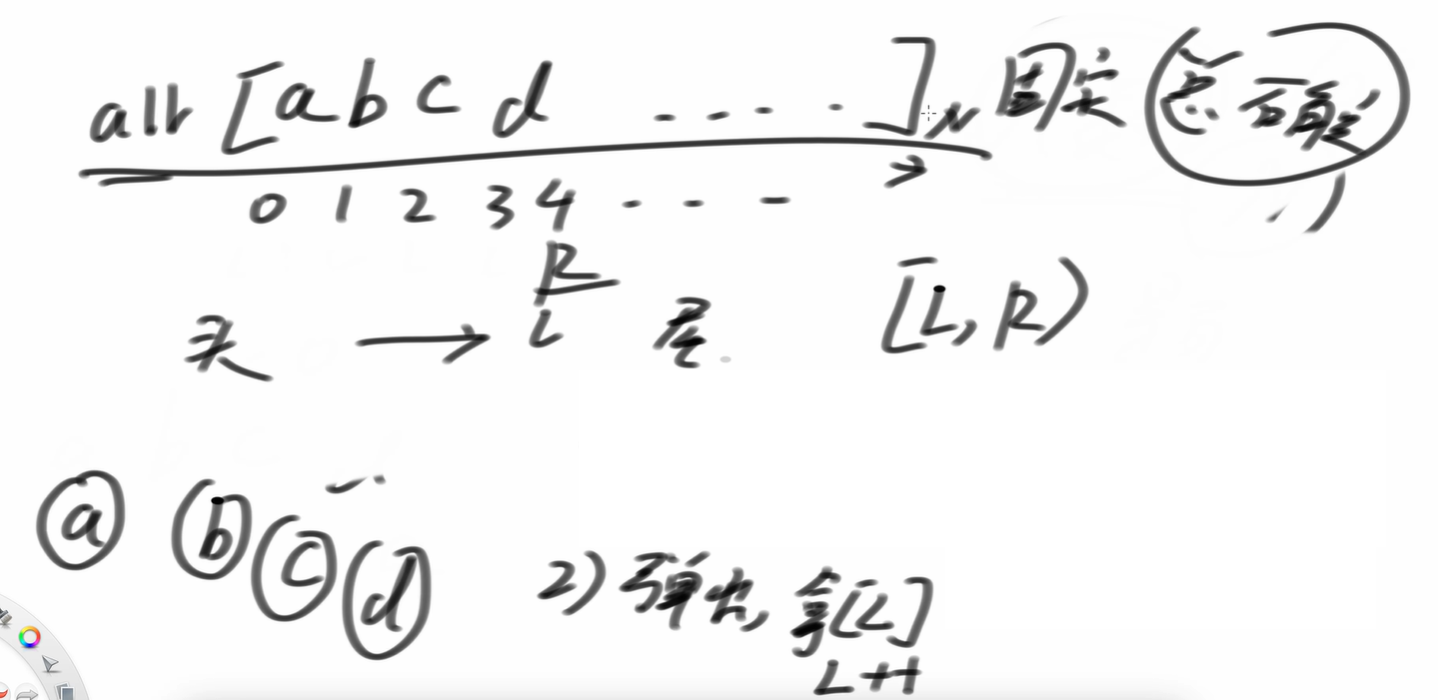
隊列是一種遵循?先進先出 (First-In, First-Out, FIFO)?原則的線性數據結構。
可以把它想象成現實生活中的排隊：最早來排隊的人，最先獲得服務并離開。在數據結構中，最早被放入（入隊）的元素，也最先被取出（出隊）。
核心操作
一個基本的隊列通常支持以下幾種操作：
-
offer(value)?(或?enqueue): 將一個元素添加到隊尾。
-
poll()?(或?dequeue): 從隊頭取出一個元素，并將其從隊列中移除。
-
peek()?(或?head): 查看隊頭的元素，但不移除它。
-
isEmpty(): 判斷隊列是否為空。
-
size()：返回隊列中元素的個數。
3）隊列的鏈表實現和數組實現
在很多語言中，都有現成的、基于鏈表實現的隊列結構。例如在 Java 中，LinkedList?類就實現了?Queue?接口。
// 直接用Java內部的實現
// 其實內部就是雙向鏈表，常數操作
public static class Queue1 {// java中的雙向鏈表LinkedList就足夠了public Queue<Integer> queue = new LinkedList<>();// 調用任何方法之前，先調用這個方法來判斷隊內是否有東西public boolean isEmpty() {return queue.isEmpty();}// 向隊內加入num, 加到隊尾public void offer(int num) {queue.offer(num);}// 從隊頭拿，從頭拿public int poll() {return queue.poll();}
}使用現成的?LinkedList?來實現隊列非常簡單，因為其雙向鏈表的結構天然支持在頭部和尾部進行 O(1) 復雜度的增刪操作，完美契合隊列的需求。
使用數組實現隊列
在筆試和面試中，更常見的要求是讓我們手動用數組來實現一個隊列。這更能考察我們對數據結構底層實現的理解。
這是一個基礎版的數組隊列實現：
// 實際刷題時更常見的寫法，常數時間好
// 如果可以確定加入操作的總次數不超過n，那么可以用
// 一般筆試、面試都會有一個明確數據量，所以這是最常用的方式
public static class Queue2 {public int[] queue;public int l; // 頭指針public int r; // 尾指針// 加入操作的總次數上限是多少，一定要明確public Queue2(int n) {queue = new int[n];l = 0;r = 0;}// 調用任何方法之前，先調用這個方法來判斷隊內是否有東西public boolean isEmpty() {return l == r;}// 入隊操作public void offer(int num) {queue[r++] = num;}// 出隊操作public int poll() {return queue[l++];}// 查看隊頭public int head() {return queue[l];}// 查看隊尾public int tail() {return queue[r - 1];}// 查看大小public int size() {return r - l;}
}代碼解析：
-
結構：我們用一個固定大小的數組?queue?作為容器，并設置兩個指針：
-
l?(left): 指向隊頭。下一個要被?poll?的元素就是?queue[l]。
-
r?(right): 指向下一個可以插入元素的位置。下一個?offer?的元素將被放入?queue[r]。
-
-
isEmpty(): 當?l?和?r?指針相遇時 (l == r)，說明隊列中沒有任何元素，隊列為空。
-
offer(num): 將元素?num?放入?r?指向的位置，然后將?r?指針后移 (r++)。
-
poll(): 返回?l?指向的元素，然后將?l?指針后移 (l++)。
這種實現的局限性：
這個基礎版的數組隊列有一個明顯的問題：指針?l?和?r?只能單向地向右移動。這意味著，即使我們?poll?了很多元素，數組前面空出來的空間也無法被重新利用。當?r?到達數組末尾時，即使隊列實際大小很小，我們也無法再?offer?新的元素了。
2）棧的介紹
像彈匣一樣，裝的時候放在上一個的上面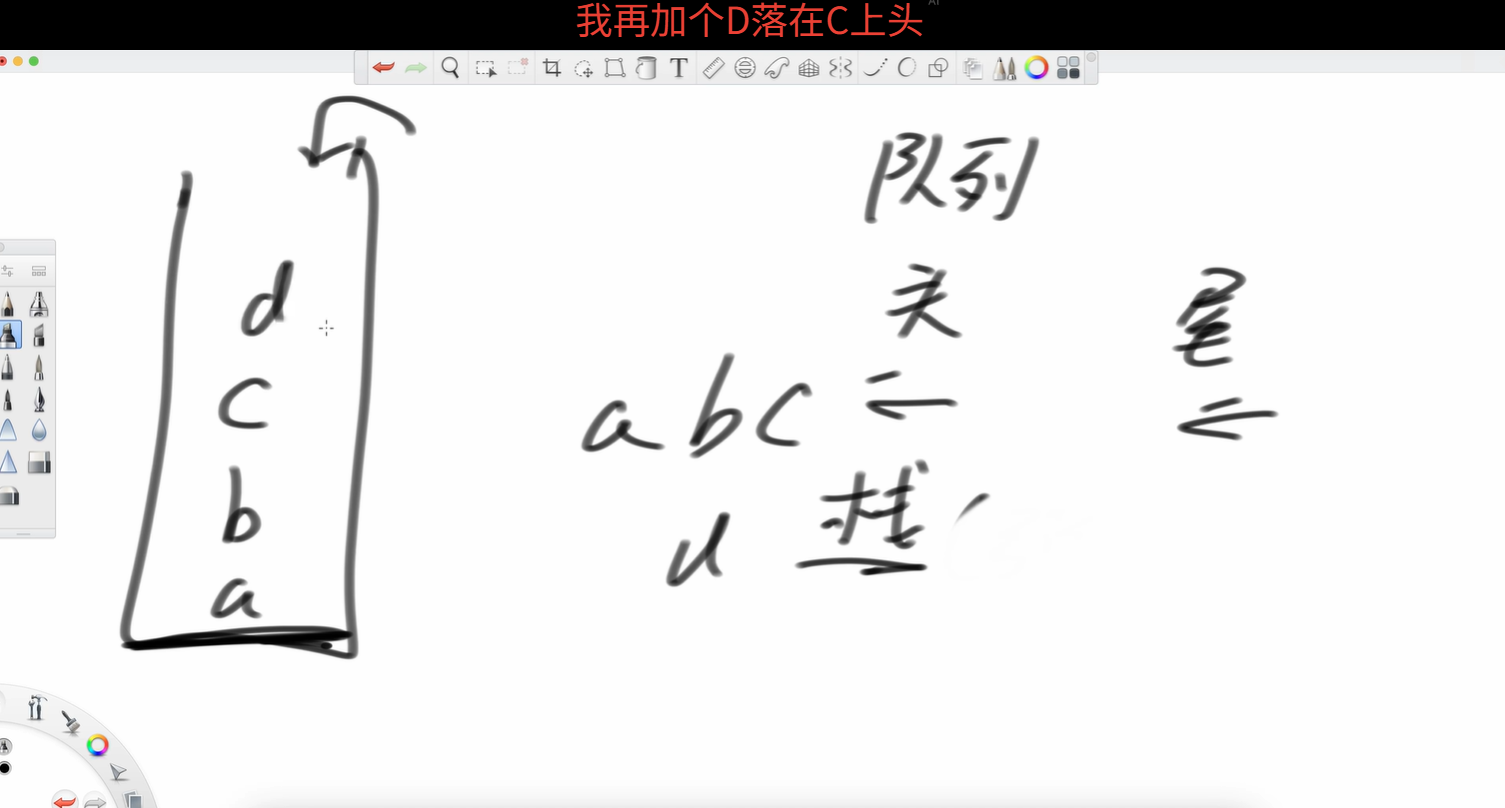
彈出的時候也是上面的先彈出。先d再c等等。
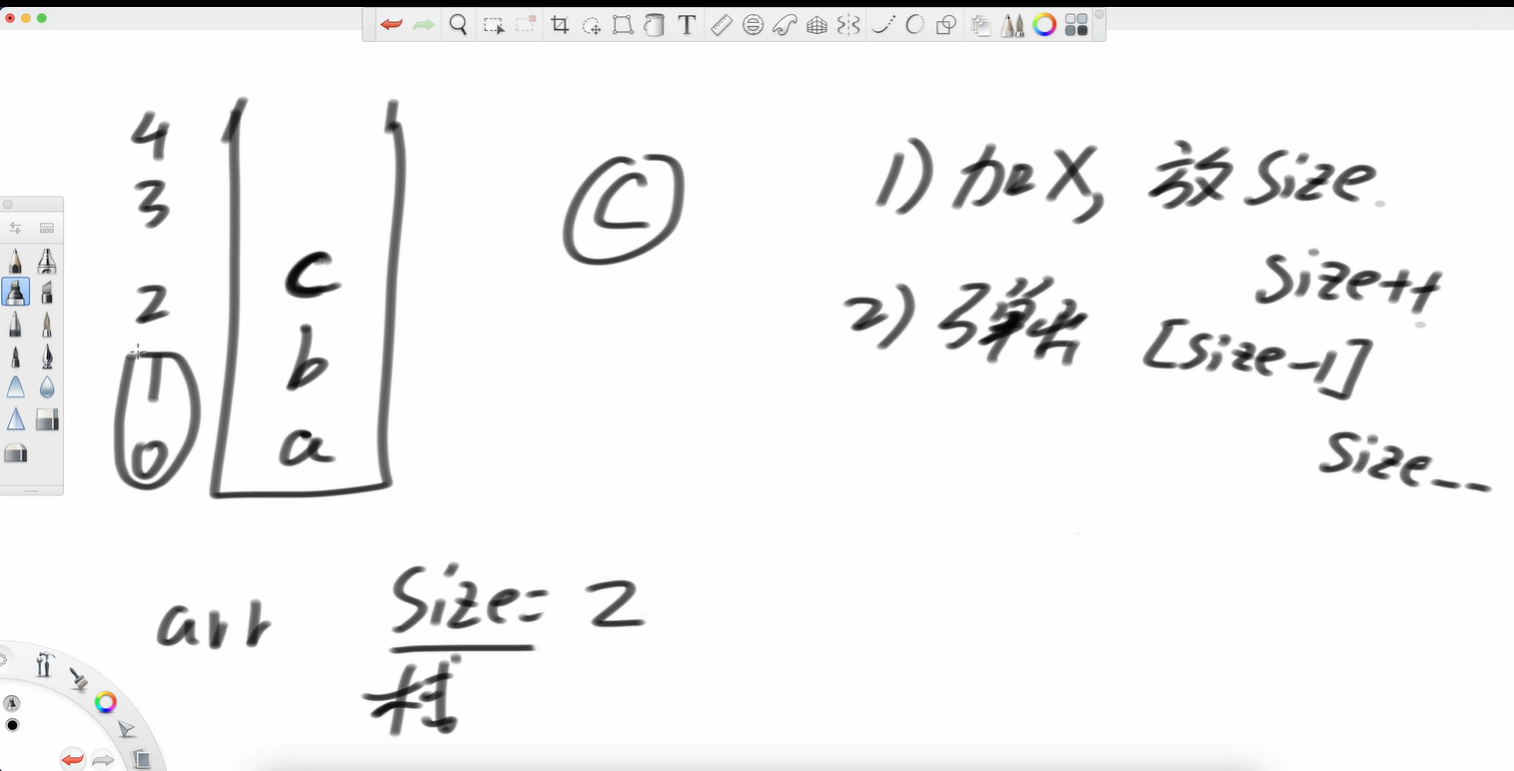和上面的隊類似。
與隊列的“先進先出”相反，棧是一種遵循?后進先出 (Last-In, First-Out, LIFO)?原則的線性數據結構。
它最經典的類比就是一摞盤子：我們總是把新盤子放在最上面，而取盤子時，也總是從最上面拿。最后放上去的盤子，最先被取走。
核心操作
一個基本的棧通常支持以下幾種操作：
-
push(value): 將一個元素壓入棧頂。
-
pop(): 從棧頂彈出一個元素，并將其從棧中移除。
-
peek(): 查看棧頂的元素，但不移除它。
-
isEmpty(): 判斷棧是否為空。
-
size()：返回棧中元素的個數。
4）棧的數組實現
使用語言內置的實現
Java 提供了?java.util.Stack?類，可以直接使用。它的底層是動態數組 (Vector)。
// 直接用Java內部的實現
// 其實就是動態數組，不過常數時間并不好
public static class Stack1 {public Stack<Integer> stack = new Stack<>();// 調用任何方法之前，先調用這個方法來判斷棧內是否有東西public boolean isEmpty() {return stack.isEmpty();}public void push(int num) {stack.push(num);}public int pop() {return stack.pop();}public int peek() {return stack.peek();}public int size() {return stack.size();}
}使用數組手動實現棧
這是在筆試、面試中考察的重點。我們通過一個數組和一個指針（或索引）來模擬棧的行為。
// 實際刷題時更常見的寫法，常數時間好
// 如果可以保證同時在棧里的元素個數不超過n，那么可以用
// 也就是發生彈出操作之后，空間可以復用
// 一般筆試、面試都會有一個明確數據量，所以這是最常用的方式
public static class Stack2 {public int[] stack;public int size; // 指針，指向下一個可插入的位置// 同時在棧里的元素個數不超過npublic Stack2(int n) {stack = new int[n];size = 0;}// 調用任何方法之前，先調用這個方法來判斷棧內是否有東西public boolean isEmpty() {return size == 0;}// 入棧public void push(int num) {stack[size++] = num;}// 出棧public int pop() {return stack[--size];}// 查看棧頂元素public int peek() {return stack[size - 1];}// 返回棧中元素數量public int size() {return size;}
}代碼解析：
-
結構：我們使用一個固定大小的數組?stack?和一個整型變量?size。這里的?size?非常巧妙，它既表示了棧中當前的元素數量，也同時扮演了棧頂指針的角色，指向下一個新元素應該被插入的位置。
-
isEmpty(): 當?size?為 0 時，棧為空。
-
push(num): 將新元素?num?放入?stack[size]?的位置，然后將?size?加一 (size++)。
-
pop(): 先將?size?減一 (--size)，使其指向當前的棧頂元素，然后返回?stack[size]。注意，數據并沒有從數組中被“清除”，但它已經變得不可訪問，后續的?push?操作會覆蓋它。這就是“空間復用”的體現。
-
peek(): 直接返回?stack[size - 1]?的值，因為?size - 1?正是當前棧頂元素的索引。
這種數組實現方式，所有操作的平均時間復雜度都是 O(1)，性能非常好。
5）環形隊列的實現 leecode622
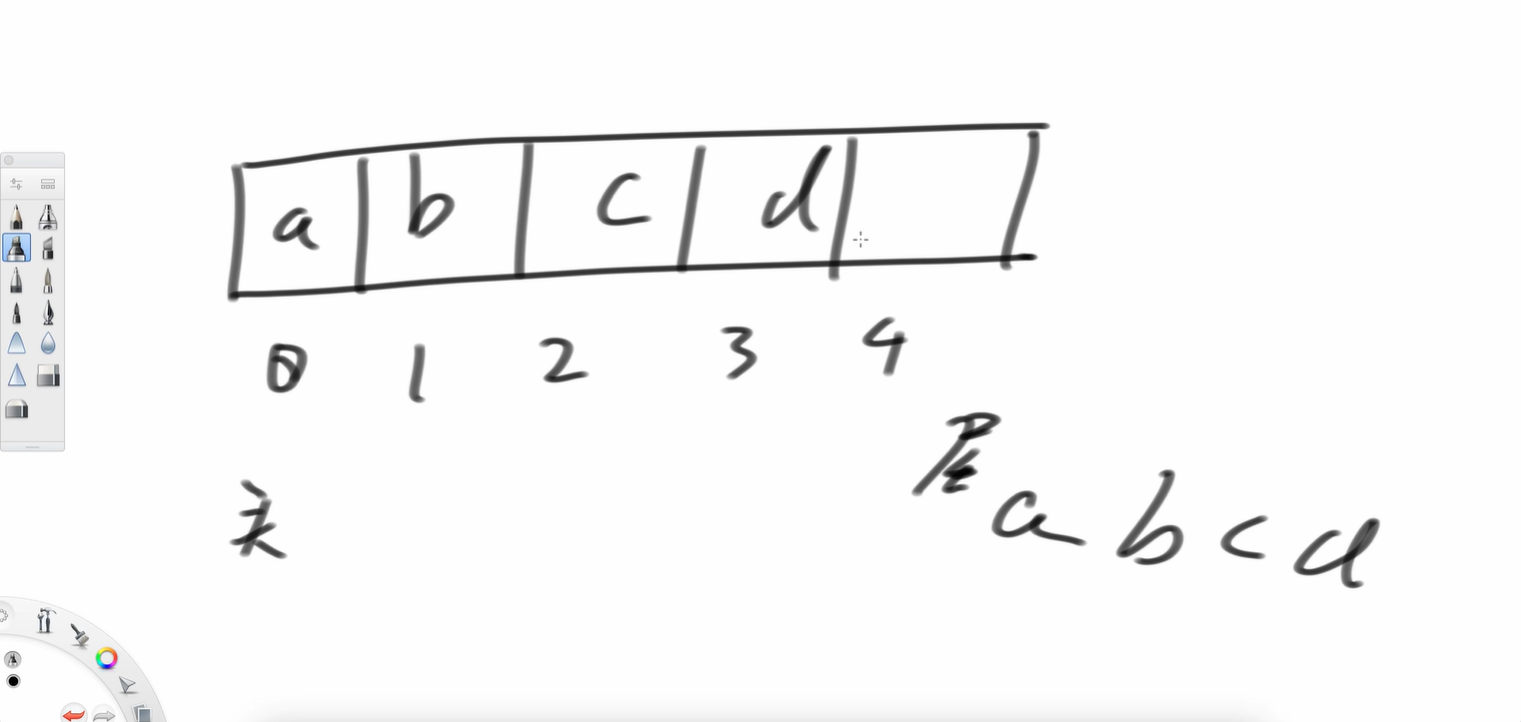
舉個例子，一共有五個位置，abcd依次放進去，a位置是頭，d位置是尾，此時我想把a彈出，就像上文中的隊列彈出，空間釋放。頭往后去。我再彈出個b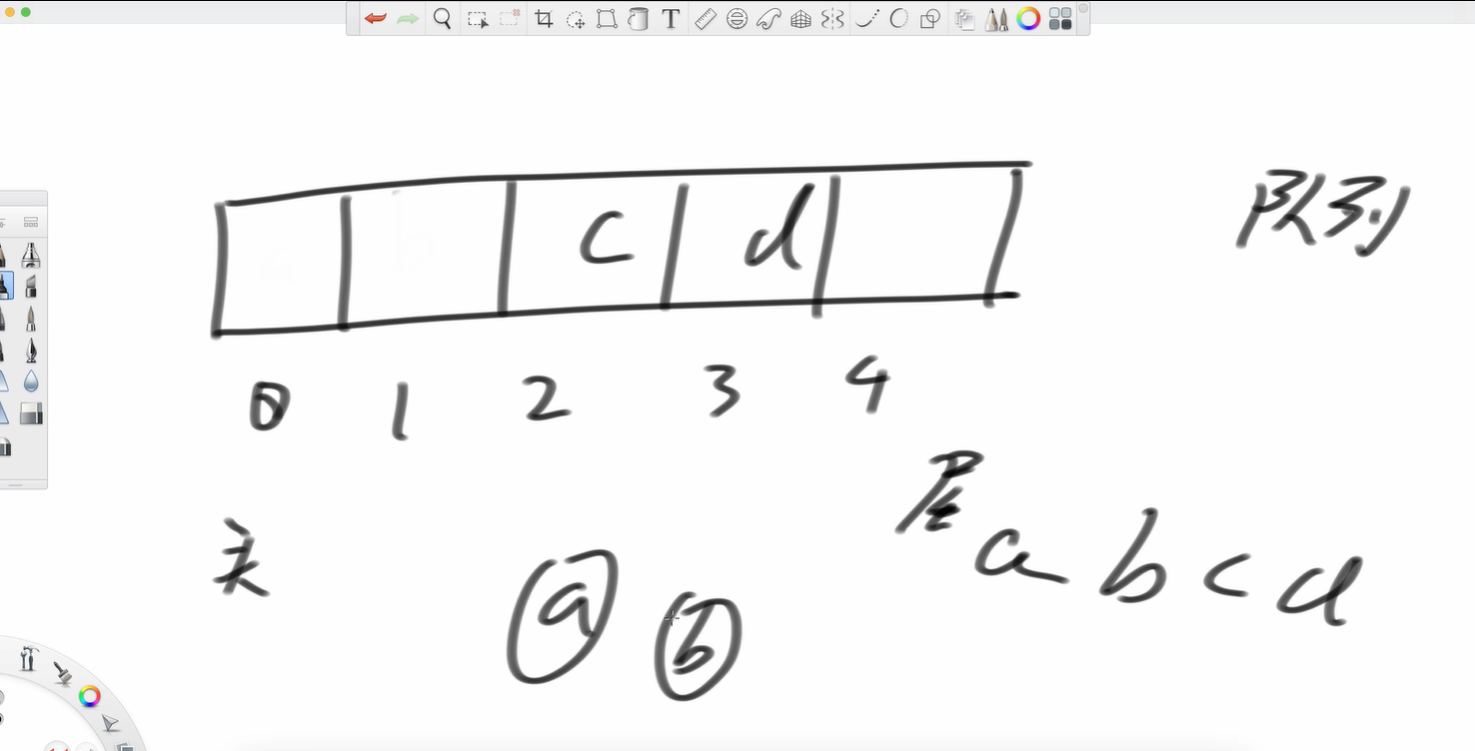
接著我再加個e呢？
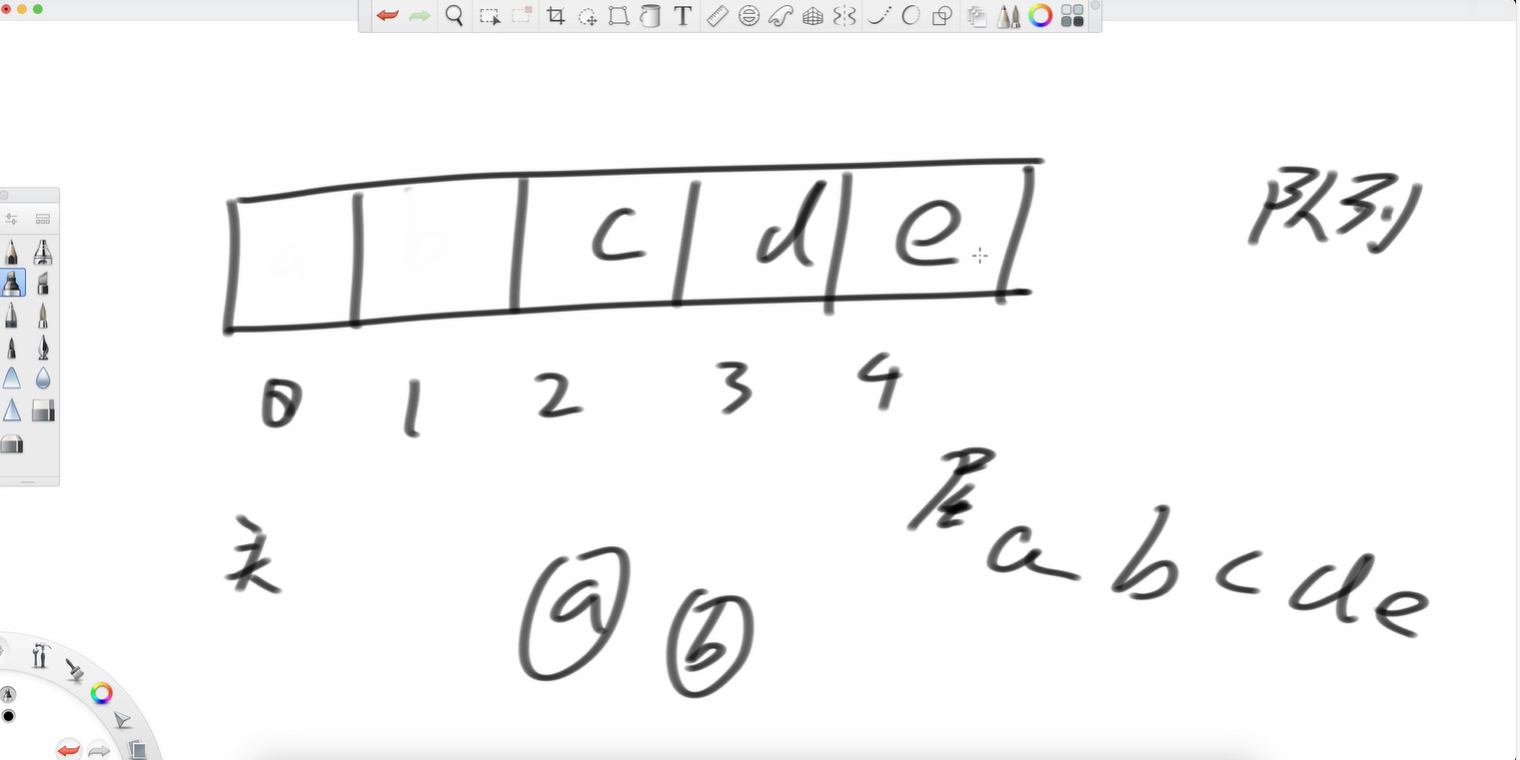
我要是再加個f呢？
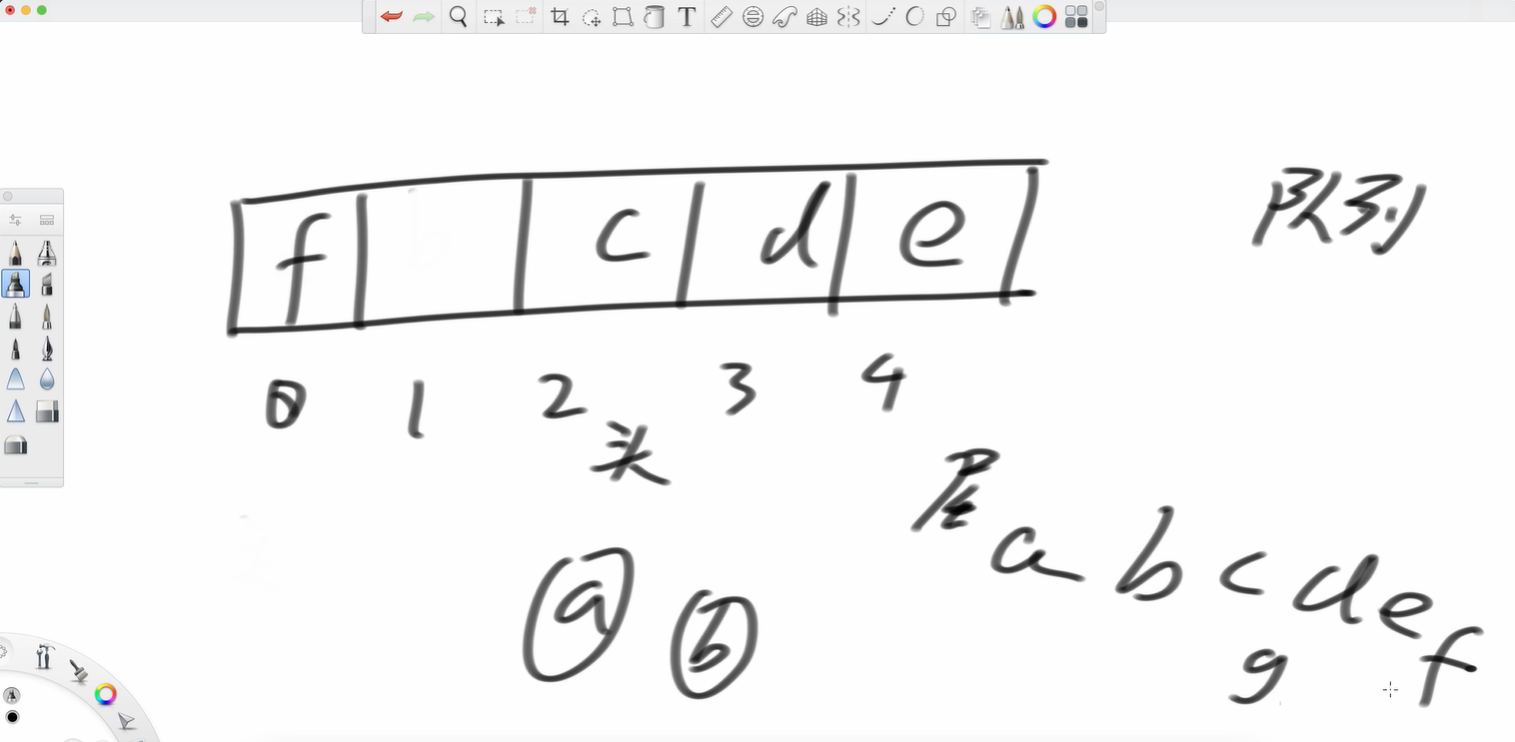
但注意，c位置是頭。
再加個g呢？
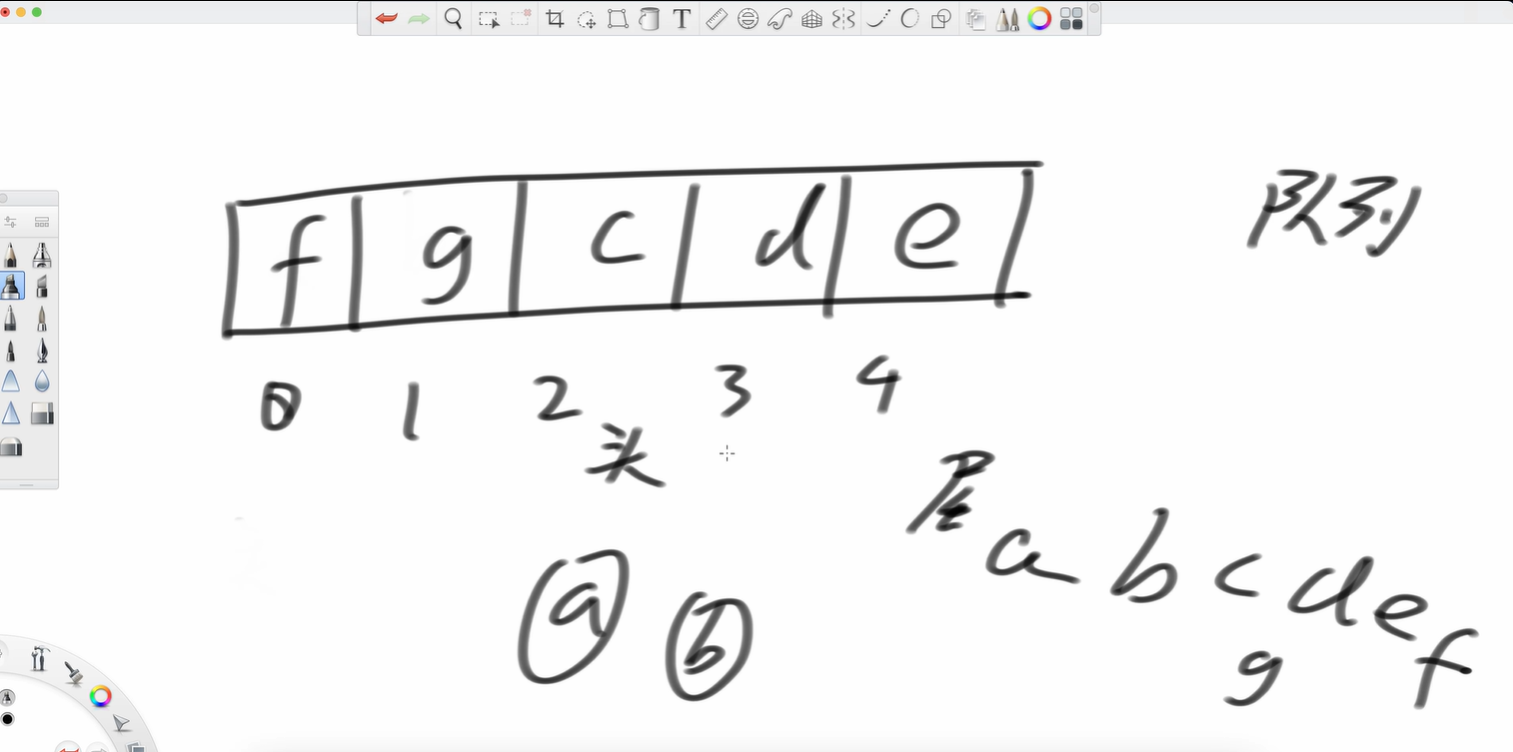
所以這就是個環形結構
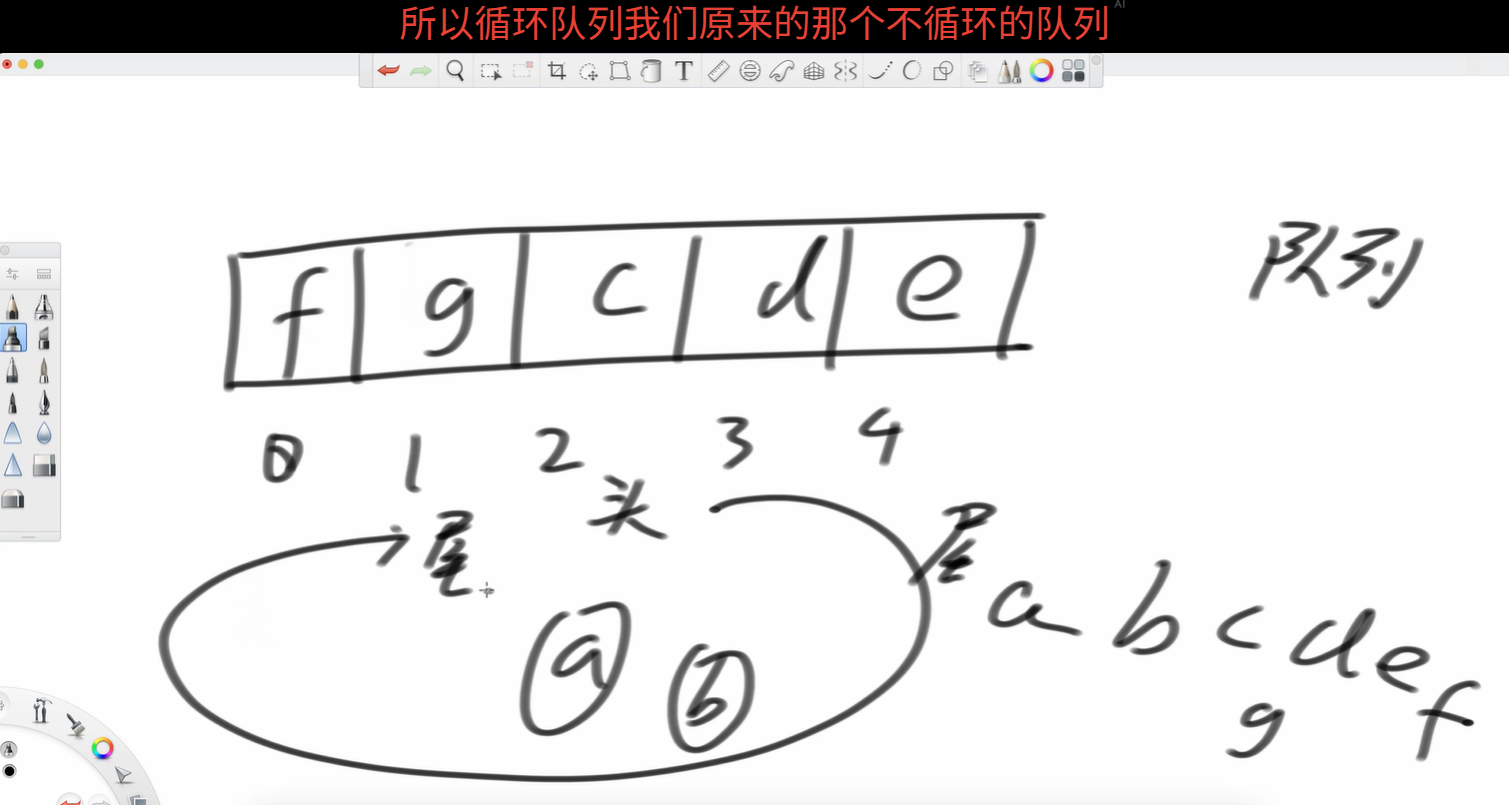所以只要你不同時多于5個在這個隊列里，就能一直保持著環形隊列繼續下去。
那怎么寫代碼呢？
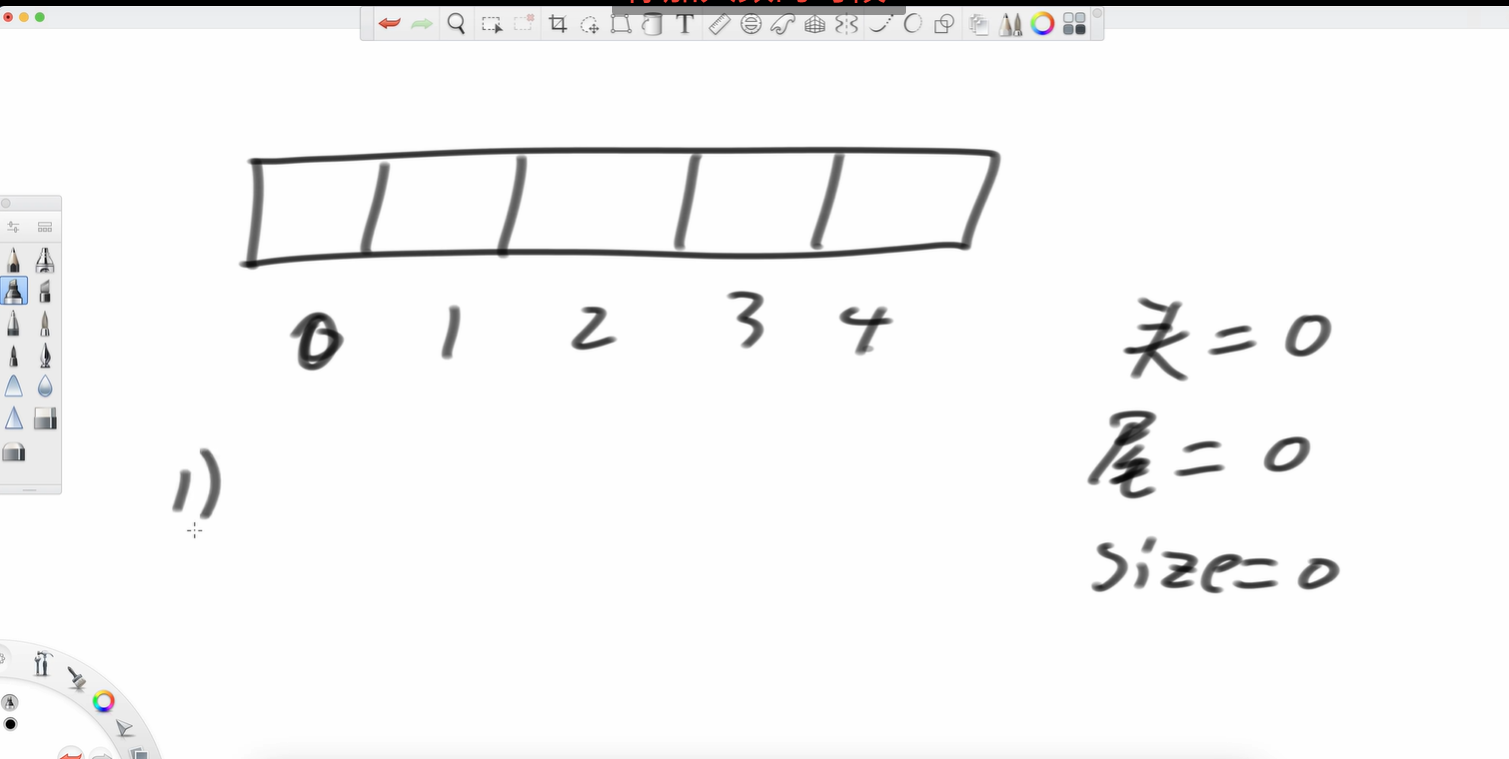
前提：size允許才能做操作一和操作二
這道題limit就是5
我現在要加入a
我再加個b，再加個c
彈出a
再加個d呢
再彈出b
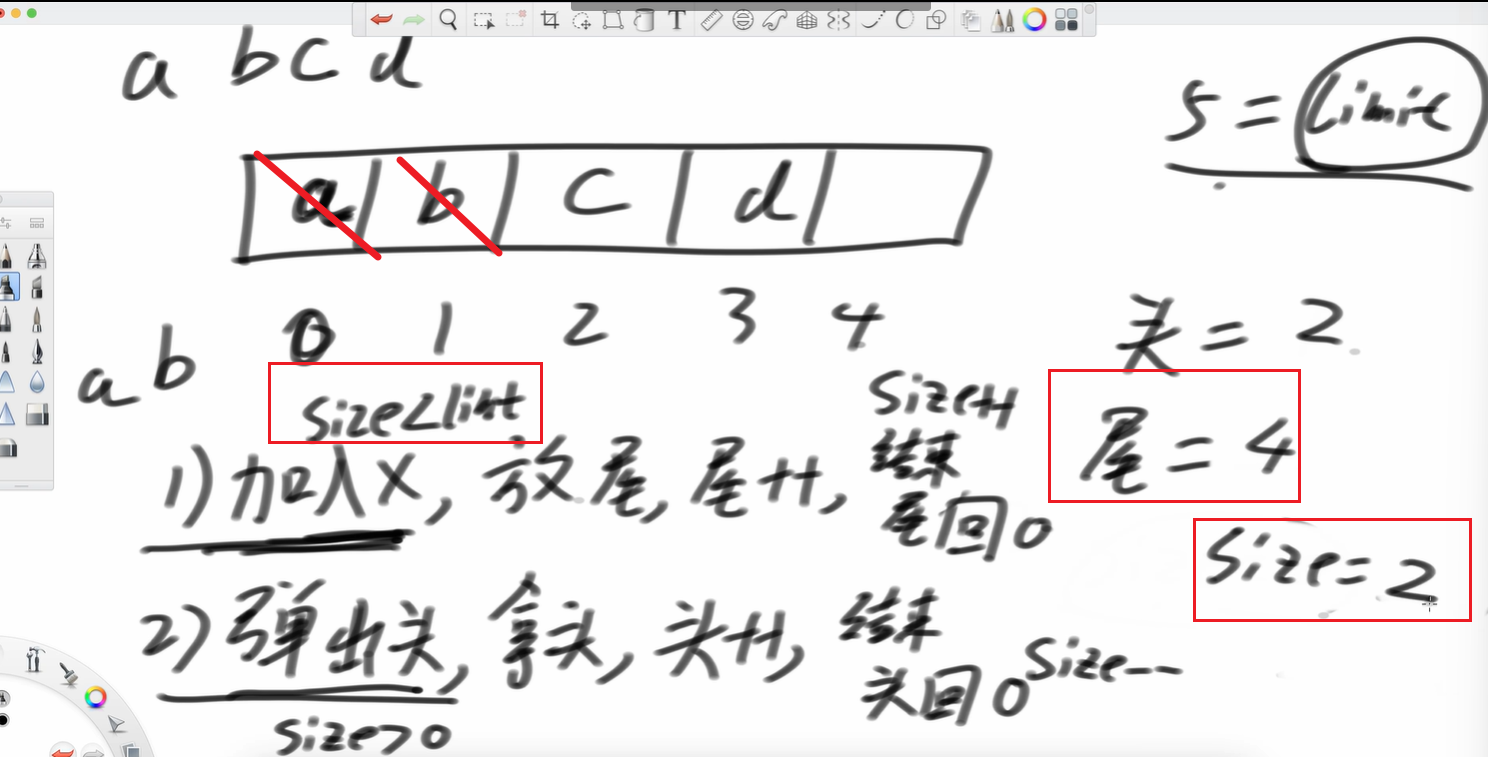
再加個e
再加個f 放到尾巴的位置，這不就復用了嗎？
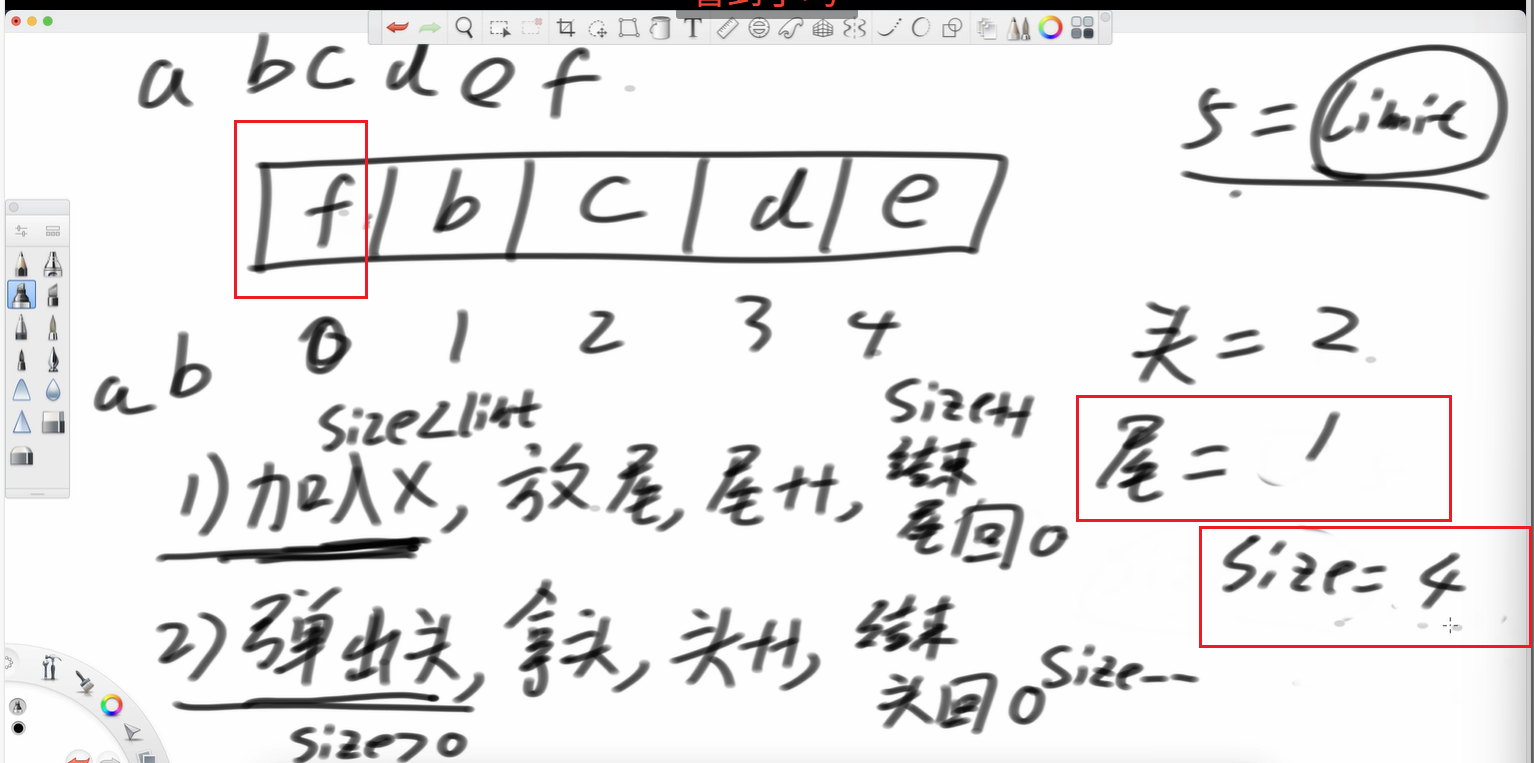https://leetcode.cn/problems/design-circular-queue/
// 設計循環隊列
// 測試鏈接 : https://leetcode.cn/problems/design-circular-queue/
class MyCircularQueue {public int[] queue;public int l; // 頭指針public int r; // 尾指針public int size; // 當前隊列大小public int limit; // 隊列容量// 構造器，設置隊列長度為 kpublic MyCircularQueue(int k) {queue = new int[k];l = r = size = 0;limit = k;}// 向循環隊列插入一個元素。如果成功插入則返回真public boolean enQueue(int value) {if (isFull()) {return false;} else {queue[r] = value;// r++, 結束了，跳回0r = r == limit - 1 ? 0 : (r + 1);size++;return true;}}// 從循環隊列中刪除一個元素。如果成功刪除則返回真public boolean deQueue() {if (isEmpty()) {return false;} else {// l++, 結束了，跳回0l = l == limit - 1 ? 0 : (l + 1);size--;return true;}}// 從隊首獲取元素。如果隊列為空，返回 -1public int Front() {if (isEmpty()) {return -1;} else {return queue[l];}}// 獲取隊尾元素。如果隊列為空，返回 -1public int Rear() {if (isEmpty()) {return -1;} else {// r 指向的是下一個要插入的位置，所以隊尾元素在 r 的前一個位置// 需要計算 r 的前一個位置，同樣要考慮循環int last = r == 0 ? (limit - 1) : (r - 1);return queue[last];}}// 檢查循環隊列是否為空public boolean isEmpty() {return size == 0;}// 檢查循環隊列是否已滿public boolean isFull() {return size == limit;}
}代碼解析
-
成員變量：
-
l?和?r：與之前一樣，分別是頭指針和尾指針。
-
limit：數組的總容量，即隊列的容量上限。
-
size：核心變量。我們引入一個?size?變量來實時記錄隊列中元素的個數。這使得判斷隊列是“空”還是“滿”變得極其簡單，避免了復雜的指針位置判斷。
-
-
enQueue(value)?入隊：
-
首先通過?isFull()?判斷隊列是否已滿。
-
queue[r] = value;：在尾指針?r?的位置放入新元素。
-
r = r == limit - 1 ? 0 : (r + 1);：環形邏輯的關鍵。更新尾指針?r。如果?r?已經到達數組的最后一個位置 (limit - 1)，則下一步就讓它跳回到 0；否則，就正常?+1。
-
size++：隊列大小加一。
-
-
deQueue()?出隊：
-
首先通過?isEmpty()?判斷隊列是否為空。
-
l = l == limit - 1 ? 0 : (l + 1);：環形邏輯的關鍵。更新頭指針?l。與?r?的邏輯完全相同，如果?l?到達末尾，就跳回 0。
-
size--：隊列大小減一。
-
-
Front()?查看隊頭：
-
如果隊列不為空，隊頭元素就是?l?指針指向的位置?queue[l]。
-
-
Rear()?查看隊尾：
-
這是最需要注意的地方。因為?r?指向的是下一個將要插入的位置，所以真正的隊尾元素在?r?的前一個位置。
-
int last = r == 0 ? (limit - 1) : (r - 1);：計算?r?的前一個位置，同樣需要考慮環形。如果?r?當前在 0，那么它的前一個位置就是數組的末尾?limit - 1；否則，就是?r - 1。
-
返回?queue[last]?即可。
-
-
isEmpty()?和?isFull()：
-
有了?size?變量，這兩個判斷變得無比清晰：size == 0?即為空，size == limit?即為滿。
-
)
