前言：

《算法磨劍: 用C++思考的藝術》 專欄

專注用C++破解算法面試真題，詳解LeetCode熱題，構建算法思維，從容應對技術挑戰。

👉 點擊關注專欄

---

《C++：從代碼到機器》 專欄

深入探索C++從語法特性至底層原理的奧秘，構建堅實而深入的系統編程知識體系。

👉 點擊關注專欄

---

《Linux系統探幽：從入門到內核》 專欄

深入Linux操作系統腹地，從命令、腳本到系統編程，探索Linux的運作奧秘。

👉 點擊關注專欄

---

作者：孤廖
學習方向：C++/Linux/算法
人生格言：折而不撓，中不為下

正文：

B3644 【模板】拓撲排序 / 家譜樹

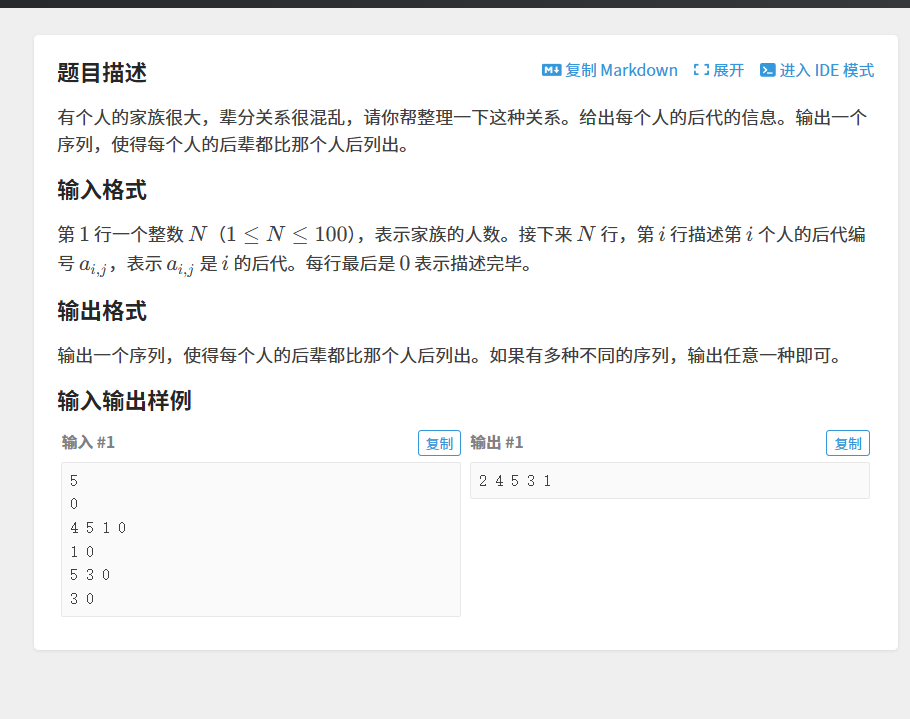
【解法】

【參考代碼】

#define _CRT_SECURE_NO_WARNINGS
//B3644 【模板】拓撲排序 / 家譜樹
#include <iostream>
#include <vector>
#include <queue>
using namespace std;const int N = 110;
vector<int> edges[N];//edges[i]:表示i節點的孩子 鄰接表（孩子表示法）
int d[N];//d[i]:i節點的入度數
int n;
int main()
{cin >> n;//處理圖的信息for (int i = 1; i <= n; i++){int j;while (cin >> j, j){edges[i].push_back(j);d[j]++;//更新每個節點的入度數}}//拓撲排序queue<int> q;//先把入度數為0 的點 加入隊列for (int i = 1; i <= n; i++) if (d[i] == 0) q.push(i);while (q.size()){int a = q.front(); q.pop();///出隊cout << a << " ";//更新入度數for (auto& e : edges[a]){d[e]--;if (d[e] == 0) q.push(e);}}return 0;
}

P2712 攝像頭

【解法】：

拓撲排序判斷是否有環。
直接跑?遍拓撲排序，然后統計?下有多少攝像頭沒有出隊。那么這些沒有出隊的攝像頭就是環??的元素。
注意：
? 有些位置可能沒有攝像頭，需要判斷?下。

【參考代碼】

#define _CRT_SECURE_NO_WARNINGS
//P2712 攝像頭#include <iostream>
#include <vector>
#include <queue>
using namespace std;
const int N = 510;
vector<int> edges[N];//edges[i]:表示i 的邊的信息即i指向的孩子
int n;//攝像頭的個數
int d[N];//d[i]:表示節點i的入度數
bool st[N];//st[i]:表示i位置是否有攝像頭
int main()
{cin >> n;//輸入攝像頭的信息 即圖的信息for (int i = 1; i <= n; i++){int x, m, y;cin >> x >> m;st[x] = true;while (m--){cin >> y;edges[x].push_back(y);//統計節點入度數d[y]++;}}//拓撲排序queue<int> q;//將入度數 為0的攝像頭入隊for (int i = 0; i <= 500; i++){if (d[i] == 0 && st[i] ) q.push(i);}while (q.size()){//將入度數為0的攝像頭 出隊int a = q.front(); q.pop();//更新與a攝像頭相關的攝像頭的入度數for (auto& e : edges[a]){d[e]--;if (st[e] && d[e] == 0) q.push(e);}}//遍歷所有位置找到是否還有沒有砸壞的攝像頭int ret = 0;//還沒砸掉的攝像頭數量for (int i = 0; i <= 500; i++){if (st[i] && d[i]) ret++;}if (ret == 0) cout << "YES " << endl;else cout << ret << endl;return 0;
}

P4017 最大食物鏈計數

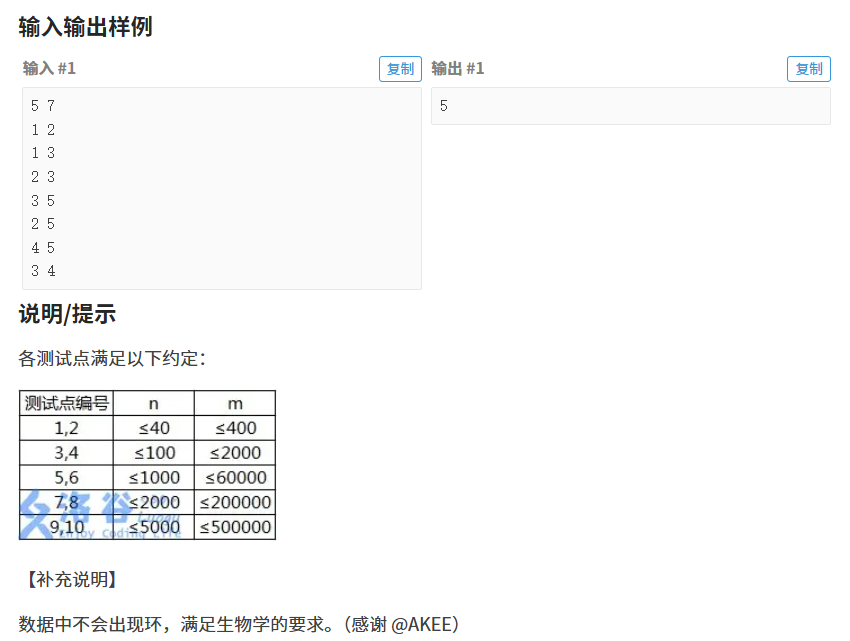
【解法】

注意審題！題?問的是?共有多少條路徑！
拓撲排序的過程中，進?動態規劃。
對于每?個節點 ，通過它的路徑為：前驅所有結點的路徑總數之和。因此，可以在拓撲排序的過程中，維護從起點開始到達每?個節點的路徑總數。

【參考代碼】

#define _CRT_SECURE_NO_WARNINGS//P4017 最大食物鏈計數#include <iostream>
#include <vector>
#include <queue>
using namespace std;
const int N = 5010,M=5e5+10,MOD= 80112002;int f[N];//f[i]:表示從生產者到i種生物的最大食物鏈條數
vector<int> edges[M];//邊數
int in[N];//in[i]:表示：i種能被多少種生物吃掉即入度數
int out[N];//out[i]:表示：i種生物能吃多少種生物即出度數
int n, m;//物種的個數 和食物鏈的條數
int main()
{cin >> n >> m;for (int i = 1; i <= m; i++){int x, y;//x->ycin >> x >> y;//統計邊的信息，和每個節點 的出入度情況edges[x]. push_back(y);in[y]++;out[x]++;}//dp+拓撲排序//初始化 初始化生產者的最大食物鏈條數 即為1queue<int> q;for (int i = 1; i <= n; i++){if (in[i] == 0){f[i] = 1;//初始化q.push(i);//生產者入隊}}while (q.size()){int a = q.front(); q.pop();//入度數為0的生物出隊//更新a的捕食者的最大生物鏈條數for (auto& e : edges[a]){//a->ein[e]--;f[e] = (f[e] + f[a]) % MOD;//模加模防止溢出if (in[e] == 0)  q.push(e);}}//統計不同食物網最大的食物鏈條數總和int ret = 0;//結果for (int i = 1; i <= n; i++){if (out[i] == 0) ret = (ret + f[i]) % MOD;//模加模防止溢出}//輸出結果cout << ret << endl;return 0;
}

3 ：P1113 雜務

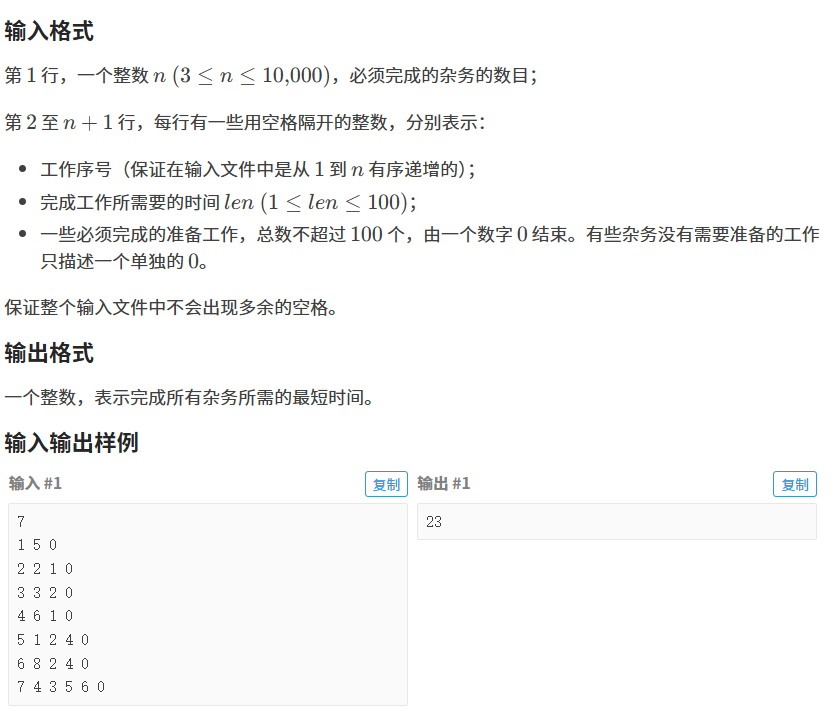
【解法】

拓撲排序的過程中，進?動態規劃。
對于每?個事件 ，完成它的最?時間為：完成前驅所有事件的最?時間中的最?值 + 當前事件的完
成時間。因此，可以在拓撲排序的過程中，維護每?個事件完成的最?時間，然后更新當前事件的最?時間。

第一種初始化下：

#define _CRT_SECURE_NO_WARNINGS
//P1113 雜務#include <iostream>
#include <vector>
#include <queue>
using namespace std;
const int N = 1e4 + 10;
int f[N];//f[i]:i雜物完成所需的最小時間
int n;//n 個雜物
vector<int> edges[N];//edges[i]:雜物i完成后能完成的雜物
int len[N];//len[i]:雜物i完成需要的時間
int in[N];//in[i]:雜物i的入度即做雜物i前 需要完成的其他雜物個數
int main()
{cin >> n;for (int i = 1; i <= n; i++){int b = 0, a = 0;//當前雜物b 作雜務b前需要完成的雜物acin >> b >> len[b];while (cin >> a, a){edges[a].push_back(b);in[b]++;}}//dp +拓撲排序//默認初始化int ret = 0;//結果queue<int> q;for (int i = 1; i <= n; i++){if (in[i] == 0) q.push(i);}while (q.size()){int pre = q.front(); q.pop();//出隊f[pre] += len[pre];ret = max(ret, f[pre]);//更新后續要完成雜物的最小時間for (auto& e : edges[pre]){in[e]--;f[e] = max(f[e], f[pre]);if (in[e] == 0) q.push(e);}}//輸出結果cout << ret << endl;return 0;
}

第二種初始化下

#define _CRT_SECURE_NO_WARNINGS
//P1113 雜務#include <iostream>
#include <vector>
#include <queue>
using namespace std;
const int N = 1e4 + 10;
int f[N];//f[i]:i雜物完成所需的最小時間
int n;//n 個雜物
vector<int> edges[N];//edges[i]:雜物i完成后能完成的雜物
int len[N];//len[i]:雜物i完成需要的時間
int in[N];//in[i]:雜物i的入度即做雜物i前 需要完成的其他雜物個數
int main()
{cin >> n;for (int i = 1; i <= n; i++){int b = 0, a = 0;//當前雜物b 作雜務b前需要完成的雜物acin >> b >> len[b];while (cin >> a, a){edges[a].push_back(b);in[b]++;}}//dp +拓撲排序//初始化int ret = 0;//結果queue<int> q;for (int i = 1; i <= n; i++){if (in[i] == 0){q.push(i);f[i] = len[i];}}while (q.size()){int pre = q.front(); q.pop();//出隊//更新后續要完成雜物的最小時間ret = max(ret, f[pre]);for (auto& e : edges[pre]){in[e]--;f[e] = max(f[e], len[e] + f[pre]);if (in[e] == 0) q.push(e);}}//輸出結果cout << ret << endl;return 0;
}

---

---

---

結語：

這篇拓撲排序專題，我們從四道洛谷題里挖出了算法 “不變的核心” 與 “多變的場景”——B3644 作為模板題，用 C++ 的vector鄰接表 +queue搭好了 Kahn 算法的基礎框架，讓 “入度維護 + 節點遍歷” 的邏輯變得直觀；P2712 攝像頭則在模板上加了 “環檢測” 的實際需求，靠 “拓撲序列長度與節點數對比” 快速破題，C++ 的st數組又幫我們精準篩選出有攝像頭的位置，避免無效計算；P4017 最大食物鏈計數更巧妙，把拓撲排序和 DP 結合，用f數組同步累加路徑數，模運算的細節處理還兼顧了數據溢出問題；而 P1113 雜務則聚焦 “最長路徑”，兩種初始化方式的對比，讓我們看清f數組維護 “前置任務最大時間” 的本質，也體會到 C++ 代碼實現的靈活性。

其實拓撲排序的魅力，就在于它能把 “依賴關系” 轉化為 “可計算的順序”，而 C++ 則是把這種思路落地的關鍵 —— 選queue還是priority_queue，用數組還是vector存狀態，甚至初始化的時機，都會影響代碼的效率與可讀性。這也是 “算法磨劍” 的意義：不只是會背模板，更是能根據題目場景，用 C++ 把算法 “磨” 成貼合需求的工具。

如果這篇解析幫你理清了拓撲排序的不同應用場景，或是對 C++ 實現細節有了新理解，不妨點個贊 + 收藏，方便后續復盤；也歡迎在評論區分享你的思考：你解 P2712 時有沒有先想到其他判環方法？P1113 的兩種初始化方式，你更偏愛哪種邏輯？后續 “算法磨劍：用 C++ 思考的藝術” 專欄還會繼續深挖圖論、動態規劃等算法的實戰場景，陪你從 “會用算法” 到 “用好算法”，在代碼里一步步精進！