注:本文為 “線性代數 | 行圖像 / 列圖像” 相關合輯。
圖片清晰度受引文原圖所限。
略作重排,未整理去重。
如有內容異常,請看原文。
MIT 線性代數筆記一 行圖像和列圖像
線性代數行圖像與列圖像解析
herosunly 已于 2022-01-25 15:34:26 修改
1. 學習背景回顧
若干年前,王清老師曾講授線性代數課程。該課程授課音量較小,后排學生難以清晰聆聽。根據模糊記憶,課程首講內容為利用行列式求解方程組(即克萊姆法則),后續依次講解矩陣的各類運算(包括加法、乘法、求逆與轉置)、初等行變換,最終涉及特征值與特征向量的求解。整個學習過程以運算訓練為主,卻未闡明各類運算的本質意義。當時曾產生疑問:線性代數的核心是否僅為各類運算規則?但該疑問未得到進一步探究。
2. 當前學習規劃
自 2018 年(大一時期)起,至今已過去十一年。2022 年新年的首要目標為系統學習李宏毅老師的《機器學習》。在學習“線性回歸”章節時,為深化對理論知識的理解,需進行公式推導,此過程涉及矩陣求導公式的應用。為掌握該知識點,制定如下學習筆記。
3. 第一講 行圖像和列圖像
3.1 線性方程組的矩陣表示
線性代數的核心問題之一是求解 nnn 元一次方程組。以二元一次方程組為例,其表達式如下:
{2x?y=0?x+2y=3\begin{cases} 2x - y = 0 \\ -x + 2y = 3 \end{cases} {2x?y=0?x+2y=3?
將上述方程組用矩陣形式表示,可得:
[2?1?12][xy]=[03]\begin{bmatrix} 2 & -1 \\ -1 & 2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 3 \end{bmatrix} [2?1??12?][xy?]=[03?]
其中,A=[2?1?12]\boldsymbol{A} = \begin{bmatrix} 2 & -1 \\ -1 & 2 \end{bmatrix}A=[2?1??12?] 稱為系數矩陣,x=[xy]\boldsymbol{x} = \begin{bmatrix} x \\ y \end{bmatrix}x=[xy?] 稱為未知數向量,等號右側的向量記為 b\boldsymbol{b}b。由此,方程組可簡化為矩陣方程:Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b。
3.2 行圖像

行圖像的幾何意義與解析幾何一致:在二維平面中,每個二元一次方程對應一條直線。繪制方程組中兩個方程對應的直線,兩條直線的交點坐標即為方程組的解。對于上述方程組,解得 x=1x = 1x=1,y=2y = 2y=2。
注:上圖由 Wolfram Alpha 繪制生成:
- 2x-y = 0 and -x+2y=3 - Wolfram|Alpha
https://www.wolframalpha.com/input/?i=2x-y+%3D+0+and+-x%2B2y%3D3
3.3 列圖像
3.3.1 列圖像的核心思想
列圖像分析的核心是將系數矩陣按列分解為若干列向量,此時求解原方程組等價于尋找列向量的線性組合,使其結果等于向量 b\boldsymbol{b}b。對于上述二元一次方程組,按列分解后可表示為:
x?[2?1]+y?[?12]=[03]x \cdot \begin{bmatrix} 2 \\ -1 \end{bmatrix} + y \cdot \begin{bmatrix} -1 \\ 2 \end{bmatrix} = \begin{bmatrix} 0 \\ 3 \end{bmatrix} x?[2?1?]+y?[?12?]=[03?]
3.3.2 線性組合的定義
“向量的線性組合”是線性代數的核心概念之一,其運算包含兩部分:
- 向量加法:需滿足平行四邊形法則或三角形法則;
- 向量數乘:對向量進行伸縮變換(系數大于 1 時向量伸展,系數大于 0 且小于 1 時向量收縮,系數小于 0 時向量反向并伸縮)。
特別地,若一組向量構成空間的“基向量”,則該空間內任意向量均可表示為這組基向量的線性組合。
3.3.3 列圖像的幾何意義
從幾何角度看,列圖像的求解目標是尋找系數 xxx 和 yyy,使得 xxx 與第一個列向量的數乘結果,與 yyy 與第二個列向量的數乘結果相加后,恰好等于向量 [03]\begin{bmatrix} 0 \\ 3 \end{bmatrix}[03?]。
3.3.4 列圖像的優勢(以三元方程組為例)
對于二元方程組,行圖像與列圖像的優勢差異不明顯;但對于多元方程組,列圖像的優勢將顯著體現。以三元一次方程組為例:
{x+2y+3z=62x+5y+2z=46x?3y+z=2\begin{cases} x + 2y + 3z = 6 \\ 2x + 5y + 2z = 4 \\ 6x - 3y + z = 2 \end{cases} ????x+2y+3z=62x+5y+2z=46x?3y+z=2?
對于矩陣方程 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b:
- 若改變向量 b\boldsymbol{b}b 的數值,行圖像中每個方程對應的平面均會發生變化,需重新分析平面間的位置關系;
- 列圖像中,系數矩陣的列向量保持不變,僅需尋找新的線性組合系數即可,求解邏輯更簡潔。
3.3.5 方程組有解的充要條件
- 核心問題:對于任意向量 b\boldsymbol{b}b,矩陣方程 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b 是否均有解?(此處“任意”指所有可能的 b\boldsymbol{b}b)
- 列圖像視角的轉化:該問題等價于“系數矩陣的列向量的線性組合是否覆蓋整個線性空間?”(選擇線性空間作為研究對象,是因為 nnn 元一次方程組的解空間本質為線性空間)。
- 無解情況的反例:若系數矩陣的列向量線性相關(例如,第三個列向量恰好等于第一個列向量減去第二個列向量),則所有列向量將共面(二維平面);若向量 b\boldsymbol{b}b 不在該平面內,則列向量的任意線性組合均無法得到 b\boldsymbol{b}b,此時方程組無解。
- 奇異矩陣的定義:當列向量線性相關時,系數矩陣 A\boldsymbol{A}A 稱為奇異陣(或不可逆矩陣)。在奇異陣條件下,并非所有 b\boldsymbol{b}b 都能使 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b 有解。
- 一般結論:對于 nnn 維線性空間,若系數矩陣的 nnn 個列向量滿足線性無關(即任意一個列向量均不能表示為其他列向量的線性組合),則對于任意 b\boldsymbol{b}b,方程組 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b 均有解;若列向量線性相關,則其線性組合無法充滿 nnn 維空間,方程組未必有解。
3.3.6 行圖像與列圖像的維度對比
從行圖像視角分析三元方程組的解:
- 有唯一解:三個平面相交于一點;
- 無解:至少兩個平面平行,或任意兩個平面的交線互相平行;
- 無窮多解:三個平面相交于一條直線。
但當空間維度升高(如 n>3n > 3n>3)時,行圖像無法直觀繪制,交點位置更難以分析。而列圖像通過“線性組合”的思想,將高維空間的解問題轉化為向量組合問題,顯著降低了分析復雜度。
3.4 總結
線性方程組可等價表示為矩陣方程 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b:
- 從“行視角”分析矩陣 A\boldsymbol{A}A,得到的是方程組中的每個獨立方程,其幾何意義為空間中的超平面;
- 從“列視角”分析矩陣 A\boldsymbol{A}A,得到的是系數矩陣的列向量,其核心是通過列向量的線性組合構造向量 b\boldsymbol{b}b。
矩陣作為融合兩種視角且邏輯自洽的數學工具,是線性代數中的重要創舉,為高維線性問題的分析提供了統一框架。
MIT—線性代數筆記 行圖像和列圖像
三少爺的鍵 編輯于 2018-10-10 13:33
1 行圖像與列圖像的基本概念(Row Picture & Column Picture)
1.1 線性方程的幾何表示(The Geometry of Linear Equations)
線性代數的核心問題之一是求解 nnn 元一次線性方程組。以二元一次線性方程組為例,其標準形式如下:
{2x?y=0?x+2y=3\begin{cases} 2x - y = 0 \\ -x + 2y = 3 \end{cases} {2x?y=0?x+2y=3?
將上述方程組表示為矩陣形式 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b,可得:
[2?1?12][xy]=[03]\begin{bmatrix} 2 & -1 \\ -1 & 2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}= \begin{bmatrix} 0 \\ 3 \end{bmatrix} [2?1??12?][xy?]=[03?]
其中各矩陣/向量的定義如下:
- 系數矩陣(Coefficient Matrix):A=[2?1?12]\boldsymbol{A} = \begin{bmatrix} 2 & -1 \\ -1 & 2 \end{bmatrix}A=[2?1??12?],用于存儲方程組中未知數的系數;
- 未知數向量(Unknown Vector):通常記為 x=[xy]\boldsymbol{x} = \begin{bmatrix} x \\ y \end{bmatrix}x=[xy?],包含方程組中所有待求的未知量;
- 常數項向量(Constant Term Vector):記為 b=[03]\boldsymbol{b} = \begin{bmatrix} 0 \\ 3 \end{bmatrix}b=[03?],包含方程組等號右側的常數項。
2 行圖像(Row Picture)
2.1 行圖像的幾何意義
行圖像基于解析幾何的思想,將線性方程組中的每個方程對應為幾何空間中的一條直線(二元情形)或一個平面(三元情形)。對于二元一次方程,通過以下步驟可確定其對應的直線:
- 求解方程的兩組解(即滿足方程的 (x,y)(x, y)(x,y) 坐標對);
- 在 x-yx\text{-}yx-y 平面上標記兩組解對應的點;
- 連接兩點形成的直線,即為該方程的行圖像。
2.2 行圖像的求解原理
線性方程組的解對應于所有方程行圖像的交點。對于本節中的二元方程組:
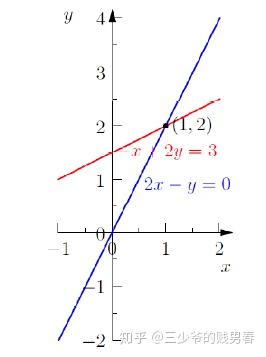
- 方程 2x?y=02x - y = 02x?y=0 的行圖像為一條直線;
- 方程 ?x+2y=3-x + 2y = 3?x+2y=3 的行圖像為另一條直線;
- 兩條直線的交點坐標 (x,y)=(1,2)(x, y) = (1, 2)(x,y)=(1,2),即為方程組的解。
3 列圖像(Column Picture)
3.1 列圖像的核心思想
列圖像的本質是將系數矩陣 A\boldsymbol{A}A 按列分解為列向量,將方程組 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b 轉化為列向量的線性組合問題。對于本節中的二元方程組,系數矩陣的列向量分解形式如下:
x?[2?1]+y?[?12]=[03]x \cdot \begin{bmatrix} 2 \\ -1 \end{bmatrix} + y \cdot \begin{bmatrix} -1 \\ 2 \end{bmatrix} = \begin{bmatrix} 0 \\ 3 \end{bmatrix} x?[2?1?]+y?[?12?]=[03?]
其中,xxx 和 yyy 是線性組合的系數(即方程組的未知數),目標是找到一組 x,yx, yx,y,使得列向量的線性組合結果等于常數項向量 b\boldsymbol{b}b。
3.2 線性組合的定義
對于給定的向量 c\boldsymbol{c}c、d\boldsymbol{d}d 及標量 xxx、yyy,表達式 xc+ydx\boldsymbol{c} + y\boldsymbol{d}xc+yd 稱為向量 c\boldsymbol{c}c 與 d\boldsymbol{d}d 的一個線性組合。線性組合是線性代數中的核心概念,貫穿整個課程體系。
3.3 列圖像的幾何意義與求解
從幾何角度看,列圖像的求解過程是:找到標量 xxx、yyy,使得列向量分別乘以 xxx、yyy 后,通過“首尾相接”的向量加法得到 b\boldsymbol{b}b。對于本節的方程組:
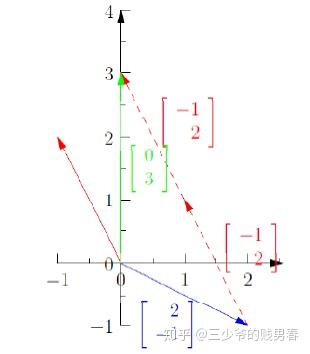
- 藍色向量為 [2?1]\begin{bmatrix} 2 \\ -1 \end{bmatrix}[2?1?],乘以 x=1x = 1x=1 后得到 1?[2?1]=[2?1]1 \cdot \begin{bmatrix} 2 \\ -1 \end{bmatrix} = \begin{bmatrix} 2 \\ -1 \end{bmatrix}1?[2?1?]=[2?1?];
- 紅色向量為 [?12]\begin{bmatrix} -1 \\ 2 \end{bmatrix}[?12?],乘以 y=2y = 2y=2 后得到 2?[?12]=[?24]2 \cdot \begin{bmatrix} -1 \\ 2 \end{bmatrix} = \begin{bmatrix} -2 \\ 4 \end{bmatrix}2?[?12?]=[?24?];
- 兩向量相加:[2?1]+[?24]=[03]=b\begin{bmatrix} 2 \\ -1 \end{bmatrix} + \begin{bmatrix} -2 \\ 4 \end{bmatrix} = \begin{bmatrix} 0 \\ 3 \end{bmatrix} = \boldsymbol{b}[2?1?]+[?24?]=[03?]=b,因此解得 x=1x = 1x=1,y=2y = 2y=2。
3.4 列向量線性組合的空間覆蓋
若任意選取標量 xxx、yyy,則列向量 [2?1]\begin{bmatrix} 2 \\ -1 \end{bmatrix}[2?1?] 與 [?12]\begin{bmatrix} -1 \\ 2 \end{bmatrix}[?12?] 的所有線性組合將布滿整個 x-yx\text{-}yx-y 平面。下圖展示了該過程的幾何直觀:
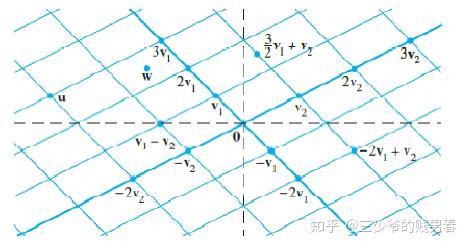
注:在 D.C.Lay 所著的《線性代數及其應用》中,曾繪制向量 v1=[?11]\boldsymbol{v}_1 = \begin{bmatrix} -1 \\ 1 \end{bmatrix}v1?=[?11?] 與 v2=[12]\boldsymbol{v}_2 = \begin{bmatrix} 1 \\ 2 \end{bmatrix}v2?=[12?] 的線性組合圖像,其整數倍線性組合的端點在平面上形成網格,直觀體現了線性組合對平面的覆蓋。該書注重通過幾何圖像輔助理解線性代數概念,英文版已更新至第 5 版,中文版由華章出版社出版。
4 三元線性方程組的行圖像與列圖像
將上述二元情形的討論擴展到三元情形,考慮如下三元一次線性方程組(選取 G. Strang 教材中的示例以匹配配圖):
{x+2y+3z=62x+5y+2z=46x?3y+z=2\begin{cases} x + 2y + 3z = 6 \\ 2x + 5y + 2z = 4 \\ 6x - 3y + z = 2 \end{cases} ????x+2y+3z=62x+5y+2z=46x?3y+z=2?
其矩陣形式為:
[1232526?31][xyz]=[642]\begin{bmatrix} 1 & 2 & 3 \\ 2 & 5 & 2 \\ 6 & -3 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix}= \begin{bmatrix} 6 \\ 4 \\ 2 \end{bmatrix} ?126?25?3?321???xyz??=?642??
4.1 三元方程組的行圖像
三元一次方程的行圖像為三維空間中的一個平面,方程組的解對應于三個平面的交點:
- 若三個平面相交于唯一一點,則方程組有唯一解;
- 若三個平面無公共交點(如存在平行平面、兩兩交線平行),則方程組無解;
- 若三個平面相交于一條直線,則方程組有無窮多解。
下圖展示了該三元方程組行圖像的幾何直觀(三個平面的相交關系):
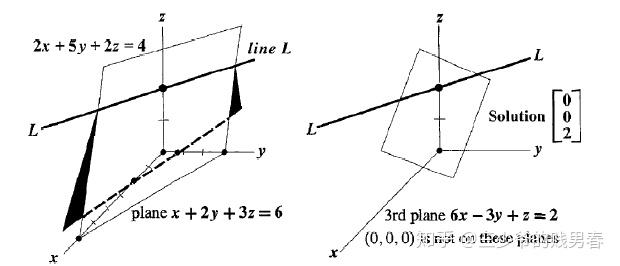
注:G. Strang 在授課中曾提及自身作圖局限性,其教材中通過“兩平面交線與第三平面相交”的分步圖示展示解的存在性;而 D.C.Lay 的教材則通過單張圖更簡潔地呈現了三維平面的相交關系。
4.2 三元方程組的列圖像
將系數矩陣按列分解,三元方程組的列圖像形式為列向量的線性組合:
x?[126]+y?[25?3]+z?[321]=[642]x \cdot \begin{bmatrix} 1 \\ 2 \\ 6 \end{bmatrix} + y \cdot \begin{bmatrix} 2 \\ 5 \\ -3 \end{bmatrix} + z \cdot \begin{bmatrix} 3 \\ 2 \\ 1 \end{bmatrix} = \begin{bmatrix} 6 \\ 4 \\ 2 \end{bmatrix} x??126??+y??25?3??+z??321??=?642??
其幾何意義為:尋找標量 x,y,zx, y, zx,y,z,使得三個列向量分別數乘后相加得到 b\boldsymbol{b}b。下圖為該線性組合的幾何示意圖:
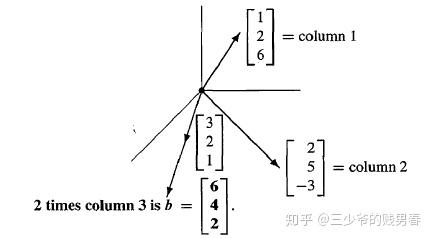
4.3 方程組解的存在性問題
對于三元方程組 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b,一個核心問題是:是否對所有的 b\boldsymbol{b}b,方程組均有解?
從列圖像角度,該問題等價于:系數矩陣 A\boldsymbol{A}A 的列向量的線性組合是否能覆蓋整個三維空間?
- 若三個列向量“線性無關”(即不存在一個列向量可由另外兩個列向量線性表示),則其線性組合可覆蓋整個三維空間,對任意 b\boldsymbol{b}b,方程組均有解;
- 若三個列向量“線性相關”(如列 3 = 列 1 + 列 2),則所有列向量共面,其線性組合僅能覆蓋該平面。若 b\boldsymbol{b}b 不在此平面內,方程組無解。此時矩陣 A\boldsymbol{A}A 稱為奇異矩陣(Singular Matrix) 或不可逆矩陣(Non-invertible Matrix)。
下圖對比了 G. Strang 與 D.C.Lay 教材中對三元方程組行圖像(平面相交關系)的作圖差異:
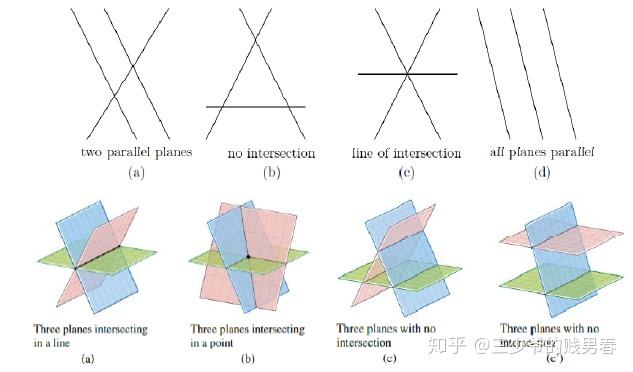
5 矩陣與向量的乘法規則
矩陣與向量的乘法 Ax\boldsymbol{A}\boldsymbol{x}Ax 有兩種等價的計算方式,分別對應列圖像與行圖像的思想。
5.1 基于列向量線性組合的計算(列圖像視角)
將矩陣 A\boldsymbol{A}A 按列分解為列向量,Ax\boldsymbol{A}\boldsymbol{x}Ax 即為列向量的線性組合。以矩陣 A=[2513]\boldsymbol{A} = \begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix}A=[21?53?] 與向量 x=[12]\boldsymbol{x} = \begin{bmatrix} 1 \\ 2 \end{bmatrix}x=[12?] 為例:
Ax=[2513][12]=1?[21]+2?[53]=[2+101+6]=[127]\boldsymbol{A}\boldsymbol{x} = \begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix} \begin{bmatrix} 1 \\ 2 \end{bmatrix} = 1 \cdot \begin{bmatrix} 2 \\ 1 \end{bmatrix} + 2 \cdot \begin{bmatrix} 5 \\ 3 \end{bmatrix} = \begin{bmatrix} 2 + 10 \\ 1 + 6 \end{bmatrix} = \begin{bmatrix} 12 \\ 7 \end{bmatrix} Ax=[21?53?][12?]=1?[21?]+2?[53?]=[2+101+6?]=[127?]
5.2 基于行向量點積的計算(行圖像視角)
將矩陣 A\boldsymbol{A}A 的每一行視為行向量,Ax\boldsymbol{A}\boldsymbol{x}Ax 的每個分量為對應行向量與 x\boldsymbol{x}x 的點積。仍以上述矩陣與向量為例:
Ax=[2513][12]=[(2?1+5?2)(1?1+3?2)]=[2+101+6]=[127]\boldsymbol{A}\boldsymbol{x} = \begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix} \begin{bmatrix} 1 \\ 2 \end{bmatrix} = \begin{bmatrix} (2 \cdot 1 + 5 \cdot 2) \\ (1 \cdot 1 + 3 \cdot 2) \end{bmatrix} = \begin{bmatrix} 2 + 10 \\ 1 + 6 \end{bmatrix} = \begin{bmatrix} 12 \\ 7 \end{bmatrix} Ax=[21?53?][12?]=[(2?1+5?2)(1?1+3?2)?]=[2+101+6?]=[127?]
兩種計算方式的結果完全一致,分別從列圖像(線性組合)與行圖像(點積)的角度詮釋了矩陣與向量乘法的本質。
矩陣的幾何意義:行圖像與列圖像的系統解析
孫梓軒 編輯于 2025-08-08 10:10?美國
1. 行空間的幾何意義與方程組解的關聯
線性方程組的行圖像,本質是將方程組中每個方程對應為其所在維度空間中的“解空間”,方程組的解即為所有解空間的交集。以下從二維情形出發,逐步剖析行圖像的幾何特征與方程組可解性的關系。
1.1 二元一次方程組的行圖像示例(有解情形)
以二元一次方程組為例:
{x+2y=52x+3y=7\begin{cases} x + 2y = 5 \\ 2x + 3y = 7 \end{cases} {x+2y=52x+3y=7?
該方程組中,每個方程對應 2 維空間(R2\mathbb{R}^2R2) 中的一條直線:
- 方程 x+2y=5x + 2y = 5x+2y=5 的解空間是一條斜率為 ?12-\frac{1}{2}?21? 的直線;
- 方程 2x+3y=72x + 3y = 72x+3y=7 的解空間是一條斜率為 ?23-\frac{2}{3}?32? 的直線。
兩條直線的交點即為方程組的解(x=?1,y=3x = -1, y = 3x=?1,y=3)。從幾何上看,只要不同方程對應的直線不平行,就存在唯一交點,方程組有唯一解。
需注意:直線在空間中沿其延伸方向無限延展,并非局限于有限坐標范圍(如 x∈[?10,10],y∈[?10,10]x \in [-10,10], y\in [-10,10]x∈[?10,10],y∈[?10,10]),因此解的存在性僅由直線的相對位置決定,與坐標范圍無關。
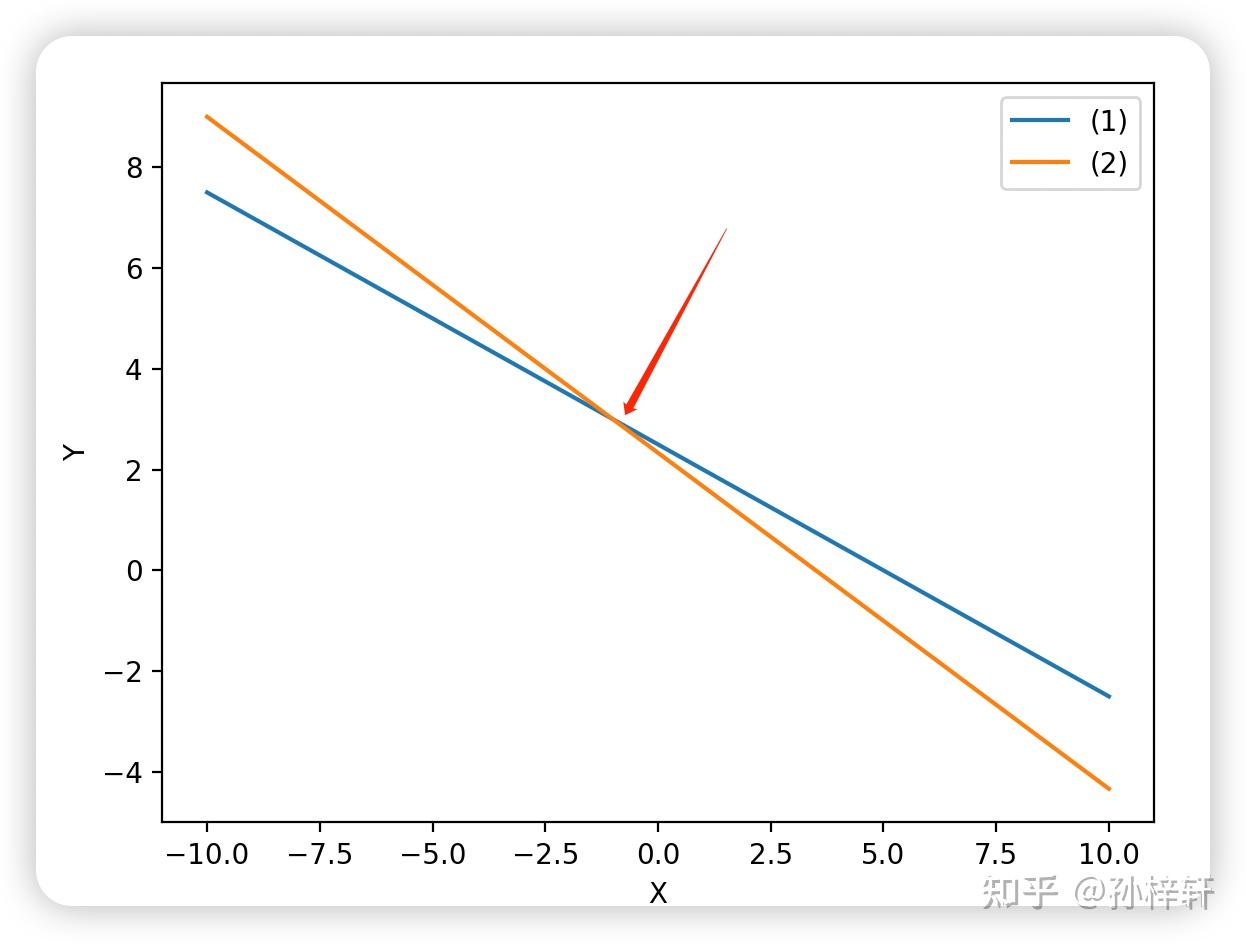
1.2 二元一次方程組的行圖像示例(無解情形)
考慮無解的二元一次方程組:
{x+2y=52x+4y=7\begin{cases} x + 2y = 5 \\ 2x + 4y = 7 \end{cases} {x+2y=52x+4y=7?
其對應的行圖像為兩條平行直線(斜率均為 ?12-\frac{1}{2}?21?),無任何交點,因此方程組無解。
從系數角度分析:兩條直線平行的充要條件是“方程中未知數系數成比例,且常數項不成比例”。具體表現為系數矩陣的兩行成比例——設系數矩陣 A=[a1b1a2b2]\boldsymbol{A} = \begin{bmatrix} a_1 & b_1 \\ a_2 & b_2 \end{bmatrix}A=[a1?a2??b1?b2??],則 a1a2=b1b2≠c1c2\frac{a_1}{a_2} = \frac{b_1}{b_2} \neq \frac{c_1}{c_2}a2?a1??=b2?b1??=c2?c1??($ c_1, c_2 $ 為常數項)。
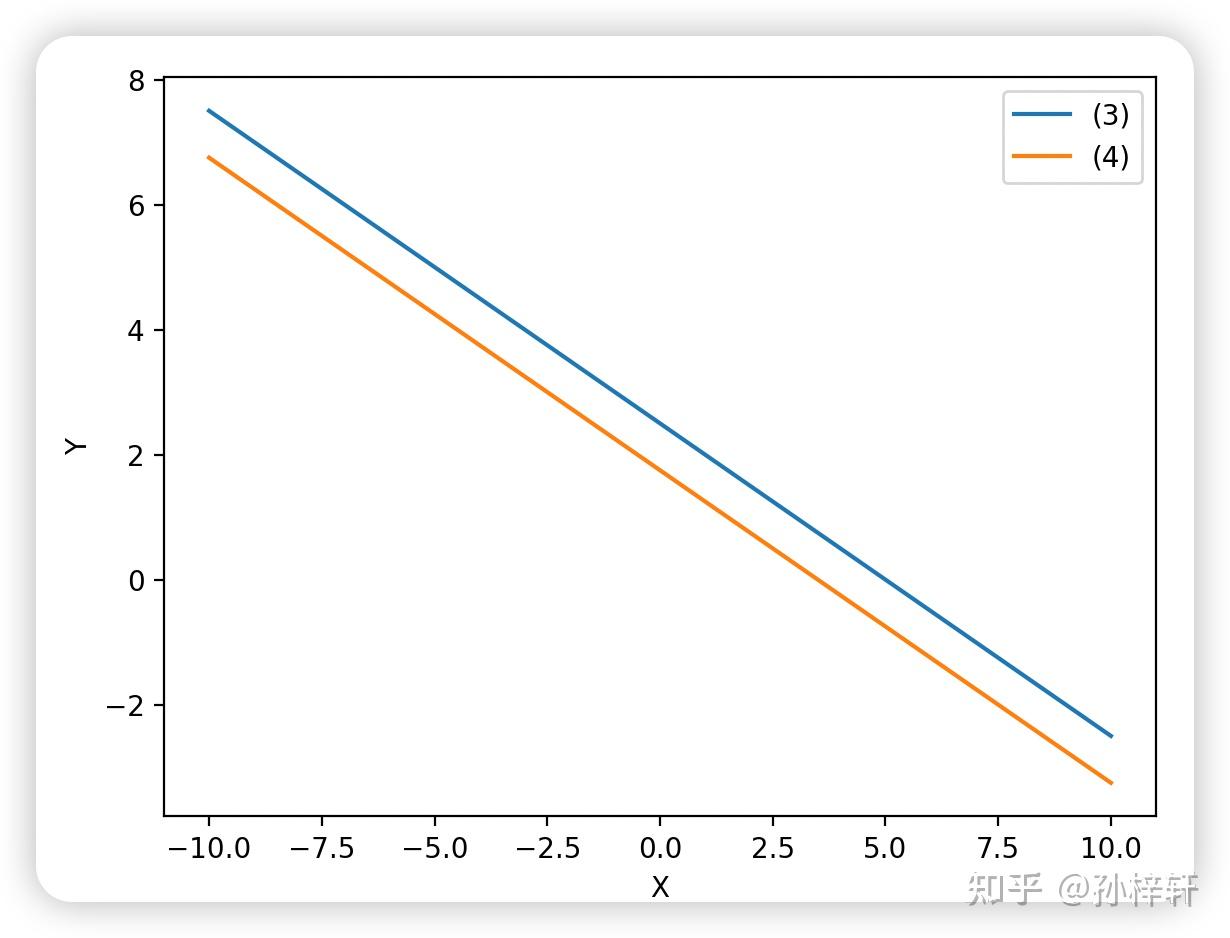
1.3 二元一次方程組的行圖像示例(無窮多解情形)
若方程組滿足“系數成比例且常數項成比例”,則對應的直線完全重合,解空間為整條直線,方程組有無窮多解。例如:
{x+2y=52x+4y=10\begin{cases} x + 2y = 5 \\ 2x + 4y = 10 \end{cases} {x+2y=52x+4y=10?
系數矩陣 A=[1224]\boldsymbol{A} = \begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix}A=[12?24?] 的兩行成比例(第二行是第一行的 2 倍),且常數項 555 與 101010 也成 2 倍比例,因此兩條直線完全重合,所有滿足 x+2y=5x + 2y = 5x+2y=5 的 (x,y)(x,y)(x,y) 均為解。
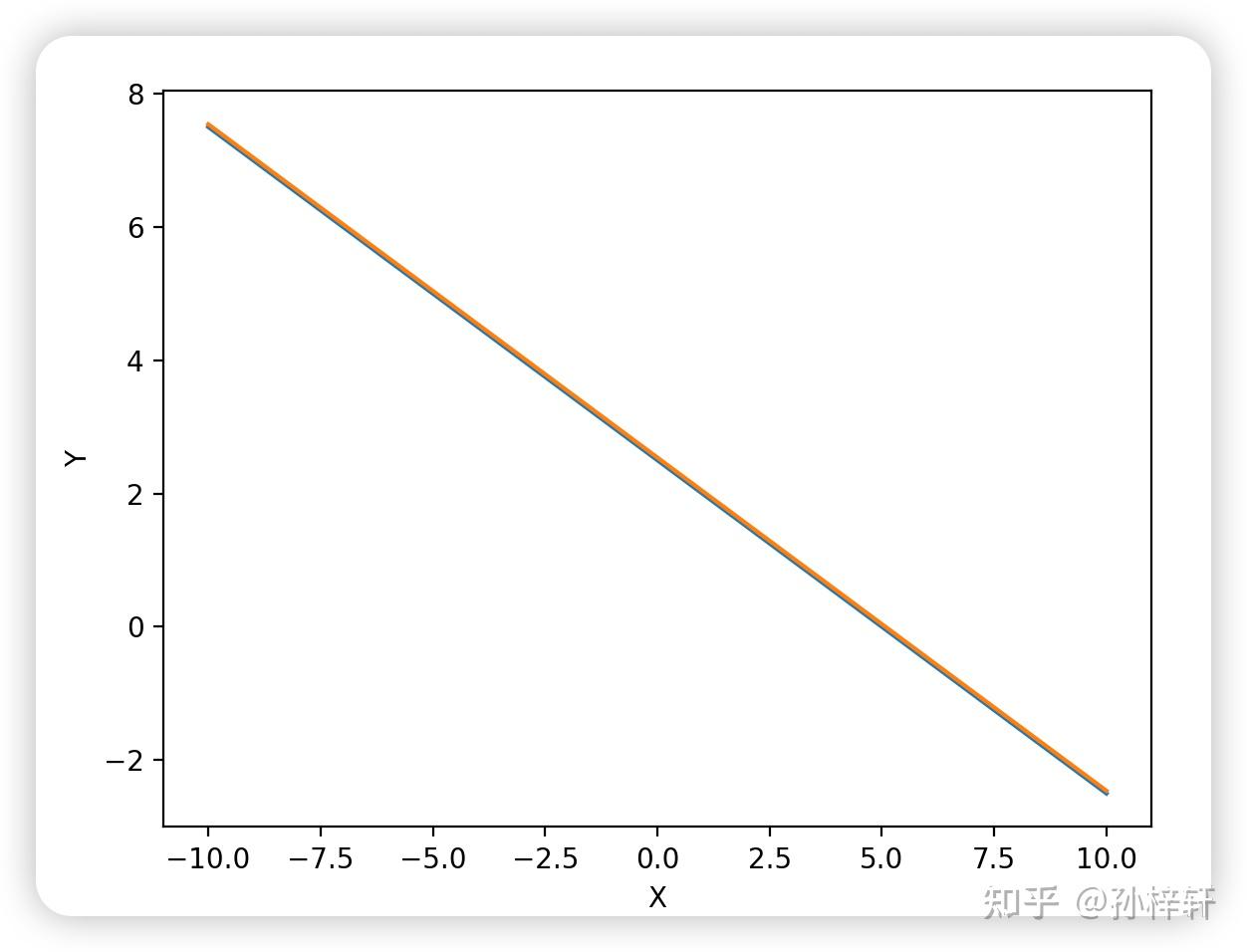
1.4 行向量的線性相關性與方程組可解性
將系數矩陣 A\boldsymbol{A}A 的每一行視為一個 行向量(如上述示例中,r1=[12],r2=[24]\boldsymbol{r}_1 = \begin{bmatrix} 1 & 2 \end{bmatrix}, \boldsymbol{r}_2 = \begin{bmatrix} 2 & 4 \end{bmatrix}r1?=[1?2?],r2?=[2?4?]),則:
- 若存在非零常數 kkk,使得 ri=k?rj\boldsymbol{r}_i = k \cdot \boldsymbol{r}_jri?=k?rj?(i≠ji \neq ji=j),則稱這兩個行向量 線性相關;
- 若不存在這樣的 kkk,則稱行向量 線性無關。
結合行圖像的幾何意義,可得出核心結論:
- 若系數矩陣 A\boldsymbol{A}A 的行向量 全部線性無關,則方程組 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b 必有解(且解唯一,二維情形下直線不平行、不重合);
- 若存在線性相關的行向量,則方程組可能無解(系數成比例但常數項不成比例),也可能有無窮多解(系數與常數項均成比例)——線性相關是“方程組無解或無窮多解”的必要非充分條件。
1.5 高維情形的行圖像推廣
行圖像的邏輯可自然推廣至高維方程組:
- 三元一次方程(3 個未知數)對應的解空間是 3 維空間(R3\mathbb{R}^3R3) 中的一個平面;
- 四元一次方程對應的解空間是 4 維空間(R4\mathbb{R}^4R4) 中的一個“超平面”(無法直觀作圖,但可通過維度邏輯分析)。
高維方程組的解即為所有超平面(或平面)的交集:交集為一點則有唯一解,交集為一條直線/平面則有無窮多解,無交集則無解。
2. 列空間的幾何意義與矩陣乘法的本質
列空間的核心是從“列向量線性組合”的視角理解矩陣乘法 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b,即將 Ax\boldsymbol{A}\boldsymbol{x}Ax 視為系數矩陣 A\boldsymbol{A}A 的列向量按 x\boldsymbol{x}x 的分量進行線性組合,最終得到 b\boldsymbol{b}b。
2.1 矩陣乘法的兩種計算視角
對于矩陣乘法 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b(其中 A∈Rm×n,x∈Rn×1,b∈Rm×1\boldsymbol{A} \in \mathbb{R}^{m \times n}, \boldsymbol{x} \in \mathbb{R}^{n \times 1}, \boldsymbol{b} \in \mathbb{R}^{m \times 1}A∈Rm×n,x∈Rn×1,b∈Rm×1),存在兩種等價的計算邏輯:
(1)行視角:行向量與列向量的點積
將 A\boldsymbol{A}A 的每一行視為行向量,與 x\boldsymbol{x}x(列向量)做點積,結果即為 b\boldsymbol{b}b 的對應分量。其通用公式為:
bi=∑k=1nAik?xk(i=1,2,…,m)b_i = \sum_{k=1}^n A_{ik} \cdot x_k \quad (i = 1,2,\dots,m) bi?=k=1∑n?Aik??xk?(i=1,2,…,m)
例如,對于 A=[1223],x=[xy]\boldsymbol{A} = \begin{bmatrix} 1 & 2 \\ 2 & 3 \end{bmatrix}, \boldsymbol{x} = \begin{bmatrix} x \\ y \end{bmatrix}A=[12?23?],x=[xy?],則:
b1=[12]?[xy]=x+2y,b2=[23]?[xy]=2x+3yb_1 = \begin{bmatrix} 1 & 2 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix} = x + 2y, \quad b_2 = \begin{bmatrix} 2 & 3 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix} = 2x + 3y b1?=[1?2?]?[xy?]=x+2y,b2?=[2?3?]?[xy?]=2x+3y
(2)列視角:列向量的線性組合
將 A\boldsymbol{A}A 的每一列視為列向量,以 x\boldsymbol{x}x 的分量為系數,對列向量進行線性組合,結果即為 b\boldsymbol{b}b。形式化表示為:
Ax=x1?a1+x2?a2+?+xn?an=b\boldsymbol{A}\boldsymbol{x} = x_1 \cdot \boldsymbol{a}_1 + x_2 \cdot \boldsymbol{a}_2 + \dots + x_n \cdot \boldsymbol{a}_n = \boldsymbol{b} Ax=x1??a1?+x2??a2?+?+xn??an?=b
其中 ak=[A1kA2k?Amk]\boldsymbol{a}_k = \begin{bmatrix} A_{1k} \\ A_{2k} \\ \vdots \\ A_{mk} \end{bmatrix}ak?=?A1k?A2k??Amk???(A\boldsymbol{A}A 的第 kkk 列列向量),xkx_kxk? 為 x\boldsymbol{x}x 的第 kkk 個分量。
以 A=[1223],x=[?13]\boldsymbol{A} = \begin{bmatrix} 1 & 2 \\ 2 & 3 \end{bmatrix}, \boldsymbol{x} = \begin{bmatrix} -1 \\ 3 \end{bmatrix}A=[12?23?],x=[?13?] 為例:
Ax=(?1)?[12]+3?[23]=[?1+6?2+9]=[57]=b\boldsymbol{A}\boldsymbol{x} = (-1) \cdot \begin{bmatrix} 1 \\ 2 \end{bmatrix} + 3 \cdot \begin{bmatrix} 2 \\ 3 \end{bmatrix} = \begin{bmatrix} -1 + 6 \\ -2 + 9 \end{bmatrix} = \begin{bmatrix} 5 \\ 7 \end{bmatrix} = \boldsymbol{b} Ax=(?1)?[12?]+3?[23?]=[?1+6?2+9?]=[57?]=b
2.2 列圖像的幾何直觀:線性組合的可視化
列圖像的本質是將“列向量線性組合得到 b\boldsymbol{b}b”的過程可視化。以上述示例為例,其幾何意義如下:
- 列向量 a1=[12]\boldsymbol{a}_1 = \begin{bmatrix} 1 \\ 2 \end{bmatrix}a1?=[12?](紅色虛線向量)經數乘 ?1-1?1 后,方向反向,得到 ?1?a1=[?1?2]-1 \cdot \boldsymbol{a}_1 = \begin{bmatrix} -1 \\ -2 \end{bmatrix}?1?a1?=[?1?2?](紅色實線向量);
- 列向量 a2=[23]\boldsymbol{a}_2 = \begin{bmatrix} 2 \\ 3 \end{bmatrix}a2?=[23?](藍色向量)經數乘 333 后,長度伸展為原來的 3 倍,得到 3?a2=[69]3 \cdot \boldsymbol{a}_2 = \begin{bmatrix} 6 \\ 9 \end{bmatrix}3?a2?=[69?];
- 將兩個數乘后的向量相加(遵循向量加法的“三角形法則”),最終得到 b=[57]\boldsymbol{b} = \begin{bmatrix} 5 \\ 7 \end{bmatrix}b=[57?](綠色向量)。
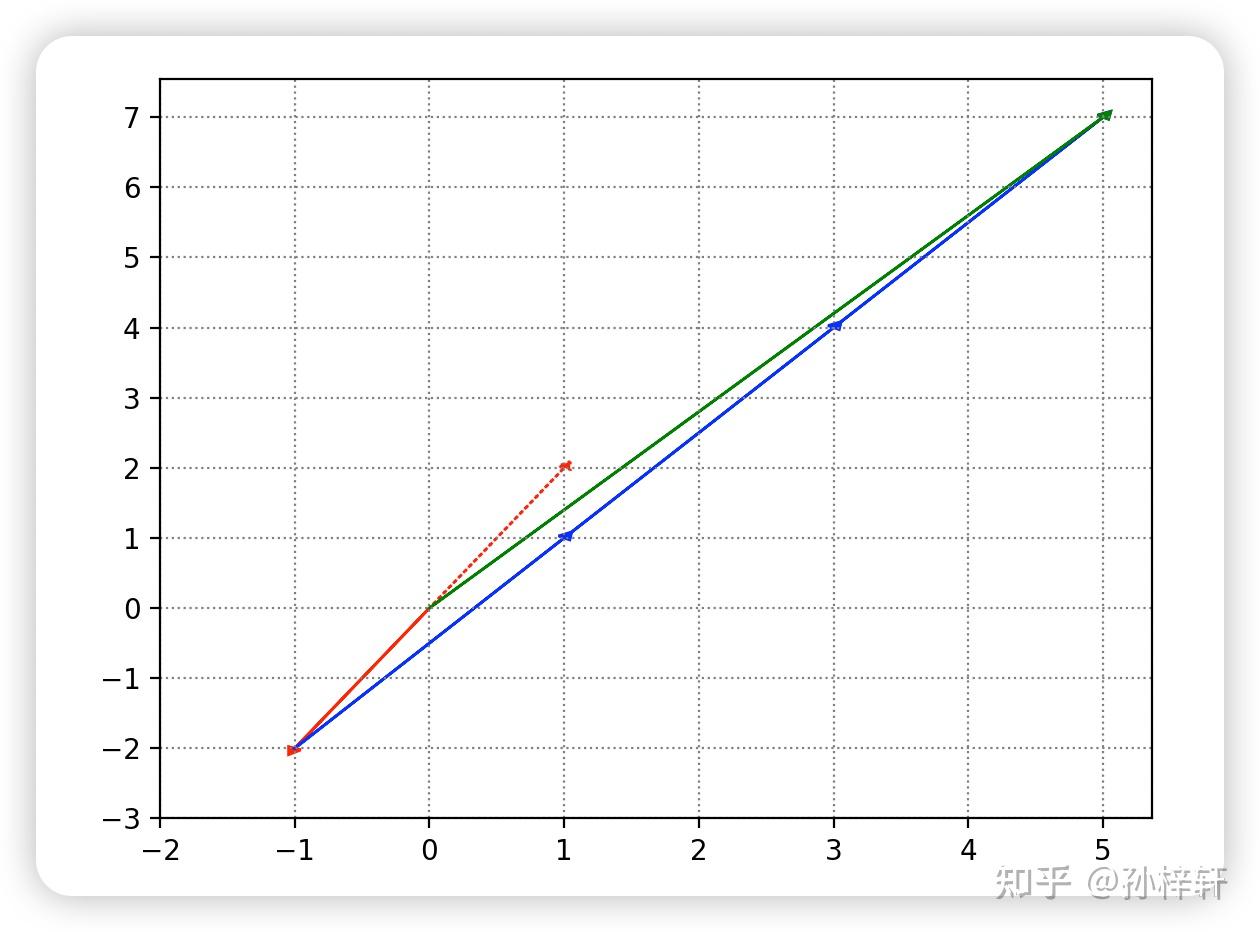
2.3 列向量的線性相關性與方程組可解性
列向量的線性相關性決定了“列向量線性組合能否覆蓋整個目標空間”,進而決定方程組 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b 是否有解。
(1)線性相關與線性無關的定義
對于 Rm\mathbb{R}^mRm 中的 nnn 個列向量 a1,a2,…,an\boldsymbol{a}_1, \boldsymbol{a}_2, \dots, \boldsymbol{a}_na1?,a2?,…,an?:
- 若存在不全為零的常數 k1,k2,…,knk_1, k_2, \dots, k_nk1?,k2?,…,kn?,使得 k1a1+k2a2+?+knan=0k_1\boldsymbol{a}_1 + k_2\boldsymbol{a}_2 + \dots + k_n\boldsymbol{a}_n = \boldsymbol{0}k1?a1?+k2?a2?+?+kn?an?=0,則稱這 nnn 個列向量 線性相關;
- 若僅當 k1=k2=?=kn=0k_1 = k_2 = \dots = k_n = 0k1?=k2?=?=kn?=0 時上式成立,則稱列向量 線性無關。
幾何上,二維空間中兩個列向量線性相關等價于“兩向量共線”(方向相同或相反);三維空間中三個列向量線性相關等價于“三向量共面”。
(2)列向量線性無關的充要條件與方程組可解性
核心結論:若系數矩陣 A\boldsymbol{A}A 的列向量 全部線性無關,則對任意 b∈Rm\boldsymbol{b} \in \mathbb{R}^mb∈Rm,方程組 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b 必有解。
原因如下:線性無關的列向量其線性組合可“充滿”整個目標空間(如二維空間中,不共線的兩個向量可組合出平面內所有向量;三維空間中,不共面的三個向量可組合出空間內所有向量)。因此,任意 b\boldsymbol{b}b 均可由這些列向量的線性組合表示,即存在對應的 x\boldsymbol{x}x 滿足 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b。
若列向量線性相關(如二維空間中兩向量共線),則其線性組合僅能覆蓋一條直線(無法充滿整個平面):
- 若 b\boldsymbol{b}b 在這條直線上,則方程組有解(無窮多解);
- 若 b\boldsymbol{b}b 不在這條直線上,則方程組無解。
2.4 行向量與列向量線性相關性的一致性
對于任意矩陣 A\boldsymbol{A}A,其行向量的線性相關性與列向量的線性相關性具有 一致性:
- 若 A\boldsymbol{A}A 的行向量全部線性無關,則其列向量也全部線性無關;
- 若 A\boldsymbol{A}A 存在線性相關的行向量,則其列向量也存在線性相關。
例如:
- 矩陣 A=[1224]\boldsymbol{A} = \begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix}A=[12?24?] 的行向量線性相關(第二行是第一行的 2 倍),列向量也線性相關(第二列是第一列的 2 倍);
- 矩陣 A=[1223]\boldsymbol{A} = \begin{bmatrix} 1 & 2 \\ 2 & 3 \end{bmatrix}A=[12?23?] 的行向量線性無關,列向量也線性無關。
這一一致性是后續“矩陣秩”概念的核心基礎(矩陣的行秩等于列秩)。
3. 解空間的維度與自由度
方程組解空間的維度(如直線、平面)本質是“自由度”的體現——自由度即“確定解所需獨立變量的個數”,解空間的維度等于自由度。
3.1 自由度與解空間維度的關系
以方程對應的解空間為例:
- 二元一次方程 y=ax+by = ax + by=ax+b(或 ax+by+c=0ax + by + c = 0ax+by+c=0):確定解 (x,y)(x,y)(x,y) 時,只需任意指定 xxx 的值,即可唯一確定 yyy 的值,因此 自由度為 1,解空間為 1 維(直線);
- 三元一次方程 z=ax+by+cz = ax + by + cz=ax+by+c(或 ax+by+cz+d=0ax + by + cz + d = 0ax+by+cz+d=0):確定解 (x,y,z)(x,y,z)(x,y,z) 時,需任意指定 xxx 和 yyy 的值,即可唯一確定 zzz 的值,因此 自由度為 2,解空間為 2 維(平面);
- nnn 元一次方程:自由度為 n?1n-1n?1,解空間為 n?1n-1n?1 維(超平面)。
本質上,方程的作用是“約束一個維度”,使原 nnn 維空間的解空間降維為 n?1n-1n?1 維。
由上述方程可知,其中一個維度的取值(一個未知變量對應一個維度,如前文的 yyy 和 zzz 可由其余兩個維度的取值(對應未知變量)唯一確定。當其余兩個維度對應的未知變量取值確定時,該維度的取值也隨之確定,即此維度不具備自由度。
具體而言,前文兩個方程中:
- 二元一次方程的自由度為 1;
- 三元一次方程的自由度為 2。
從空間維度與自由度的對應關系來看:
- 二維空間的自由度為 2;
- 三維空間的自由度為 3。
而上述方程對應的自由度(1 和 2)均低于其所在空間的自由度,因此方程的解空間發生維度退化(簡稱“降維”):
- 二元一次方程的解空間退化為自由度為 1 的空間,幾何形態表現為一條直線;
- 三元一次方程的解空間退化為自由度為 2 的空間,幾何形態表現為一個平面。
3.2 自由度與方程組解的個數
方程組解的個數由“所有方程約束后的總自由度”決定:
- 若總自由度為 0(如兩個不平行的二元一次方程,約束兩個維度),則解空間為 0 維(一個點),方程組有唯一解;
- 若總自由度為 k>0k > 0k>0(如兩個重合的二元一次方程,僅約束一個維度),則解空間為 kkk 維(一條直線或平面),方程組有無窮多解;
- 若方程之間存在矛盾(如兩個平行的二元一次方程),則無滿足所有約束的解,方程組無解。
4. 最后
本文通過行圖像與列圖像的雙視角,揭示了矩陣的幾何意義與方程組可解性的核心邏輯,關鍵結論可概括為:
- 行圖像:方程組的解是各方程對應解空間(直線、平面或超平面)的交集,解的存在性由行向量的線性相關性決定;
- 列圖像:矩陣乘法 Ax=b\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}Ax=b 是列向量的線性組合,解的存在性由列向量的線性相關性決定;
- 一致性:矩陣的行向量與列向量線性相關性一致,這是“矩陣秩”的核心屬性。
上述提到的方程組是否一定有解、維度、矩陣的秩(rank,反映線性無關向量的最大個數)以及矩陣是否可逆(方程組有唯一解的特殊情形),都是有相關性的。
via:
-
MIT線性代數筆記一 行圖像和列圖像_為什么行圖和列圖維度不一樣-CSDN博客
https://blog.csdn.net/herosunly/article/details/88698381- ref
- Gilbert Strang. Introduction to Linear Algebra (5th Edition). Wellesley-Cambridge Press.
- David C. Lay. Linear Algebra and Its Applications (5th Edition). Pearson.
- deep learning - Hung-yi Lee
https://speech.ee.ntu.edu.tw/~tlkagk/courses_ML19.html - 麻省理工 線性代數 (MIT 18.06, Linear Algebra, Gilbert Strang)【中英】_bilibili
https://www.bilibili.com/video/av34573725/ - 哈爾濱工業大學 矩陣分析 全72講 主講-嚴質彬 視頻教程_bilibili
https://www.bilibili.com/video/av11355346/
- ref
-
MIT—線性代數筆記01 行圖像和列圖像 - 知乎
https://zhuanlan.zhihu.com/p/45708880 -
矩陣的幾何意義(行圖像和列圖像) - 知乎
https://zhuanlan.zhihu.com/p/618370114













 在Window 系統的默認安裝配置)


,js(基本類型、運算符典例))
)

)