B題全部更新完畢 包含完整的文章+全部問題的代碼、結果、圖表

完整內容請看文末最后的推廣群

NIPT 的時點選擇與胎兒的異常判定
摘要
在問題一中，我們以無創產前檢測（NIPT）數據為研究對象，圍繞“胎兒 Y 染色體濃度”(記為 (V)) 隨孕周 (G) 與 BMI (B) 的變化規律展開系統論證。為克服重復測量與個體差異帶來的估計偏倚，我們以混合效應模型為主線，以對數幾率變換與半參數平滑為兩翼，構建“LME / logitLME / GAM”互證框架，并以極大似然推斷、懲罰樣條與交互效應檢驗為理論支撐。
在問題二的求解過程中，我們圍繞“男胎、BMI 分組、最優檢測孕周”這一核心任務，建立了概率—風險—決策的完整框架：首先通過邏輯回歸結合 B 樣條刻畫“達標概”與“通過概率 ”，并綜合二者得到一次成功率；其次利用重復檢測信息估計復檢延遲，將檢測結果映射為“期望風險”函數，以反映早、中、晚孕階段的風險差異；最后在 BMI 維度上進行候選分箱與復雜度懲罰下的最優切分，并在每組內搜索最小化期望風險的檢測時點，從而得到兼具統計合理性與臨床可操作性的“BMI 分組—推薦孕周”方案。
本文針對問題三，通過數據預處理、特征工程和數學建模，提出了一種優化NIPT檢測時點選擇的解決方案。首先，我們利用廣義估計方程（GEE）模型對多次檢測數據進行建模，采用Logit回歸預測孕婦在不同孕周的達標概率。然后，通過構建期望風險最小化的優化問題，選擇出每個BMI分組的最優檢測時點。最后，基于模型結果，我們進行了敏感性分析和可視化展示，驗證了模型的穩健性并為臨床決策提供了科學依據。
在問題四的求解過程中，我們針對女胎樣本的非整倍體判定，構建了一套“質控分流—規則判定—模型化灰區”的三段式框架。首先，通過對讀段數、GC 含量、比對比例等指標建立質量控制門檻，將低質量樣本直接標記為“需復檢”；其次，利用 Z 值的統計學性質設定高低閾值，對置信度足夠高的樣本進行快速判定；最后，對于處于邊界區間的灰區樣本，引入邏輯回歸模型，并結合概率校準與靈敏度優先的閾值優化方法進行判別。該方法既保持了統計學規則的可解釋性，又發揮了機器學習在復雜情境下的靈活性.
關鍵詞：混合效應模型、對數幾率變換、廣義加性模型、邏輯回歸

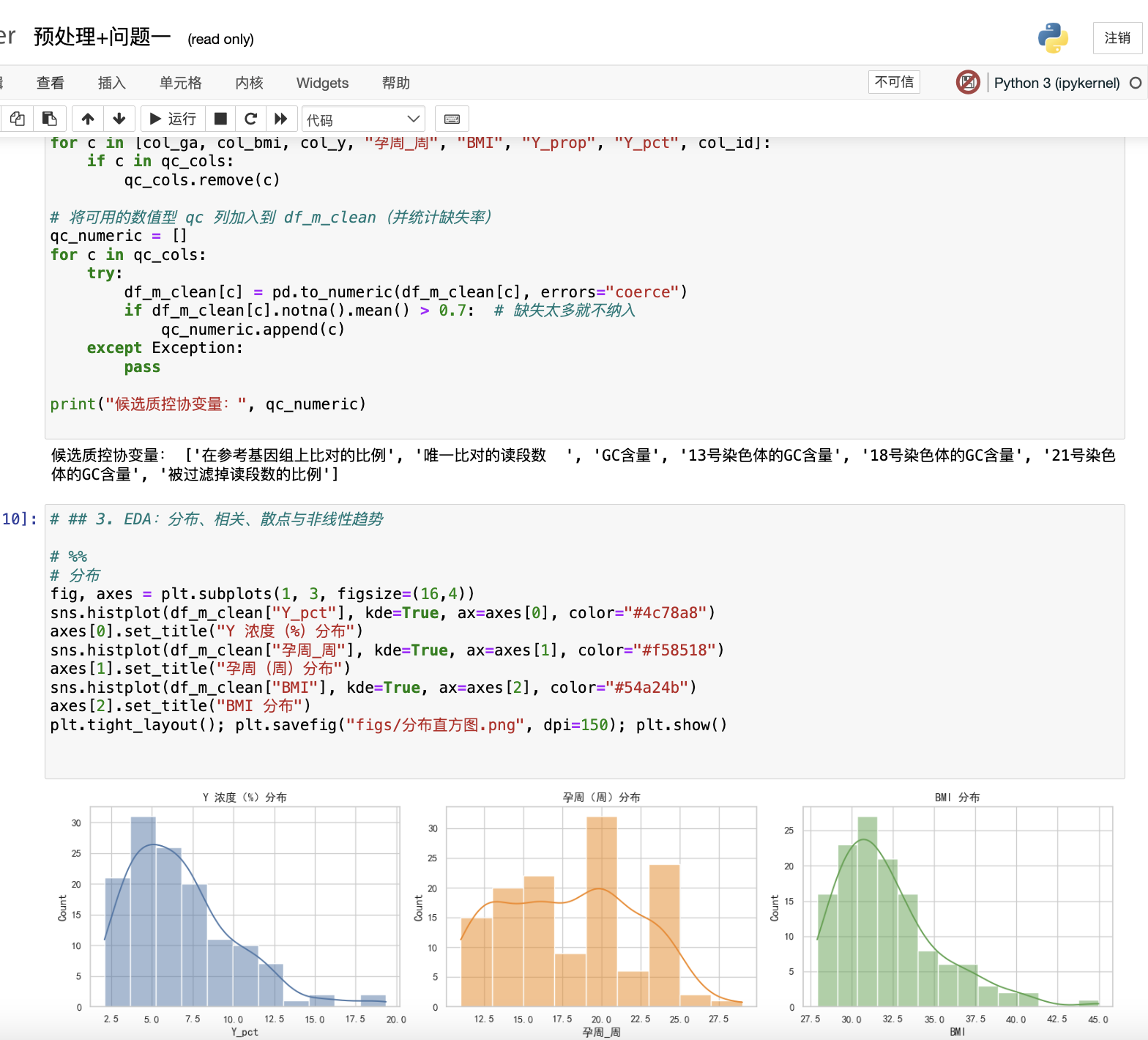
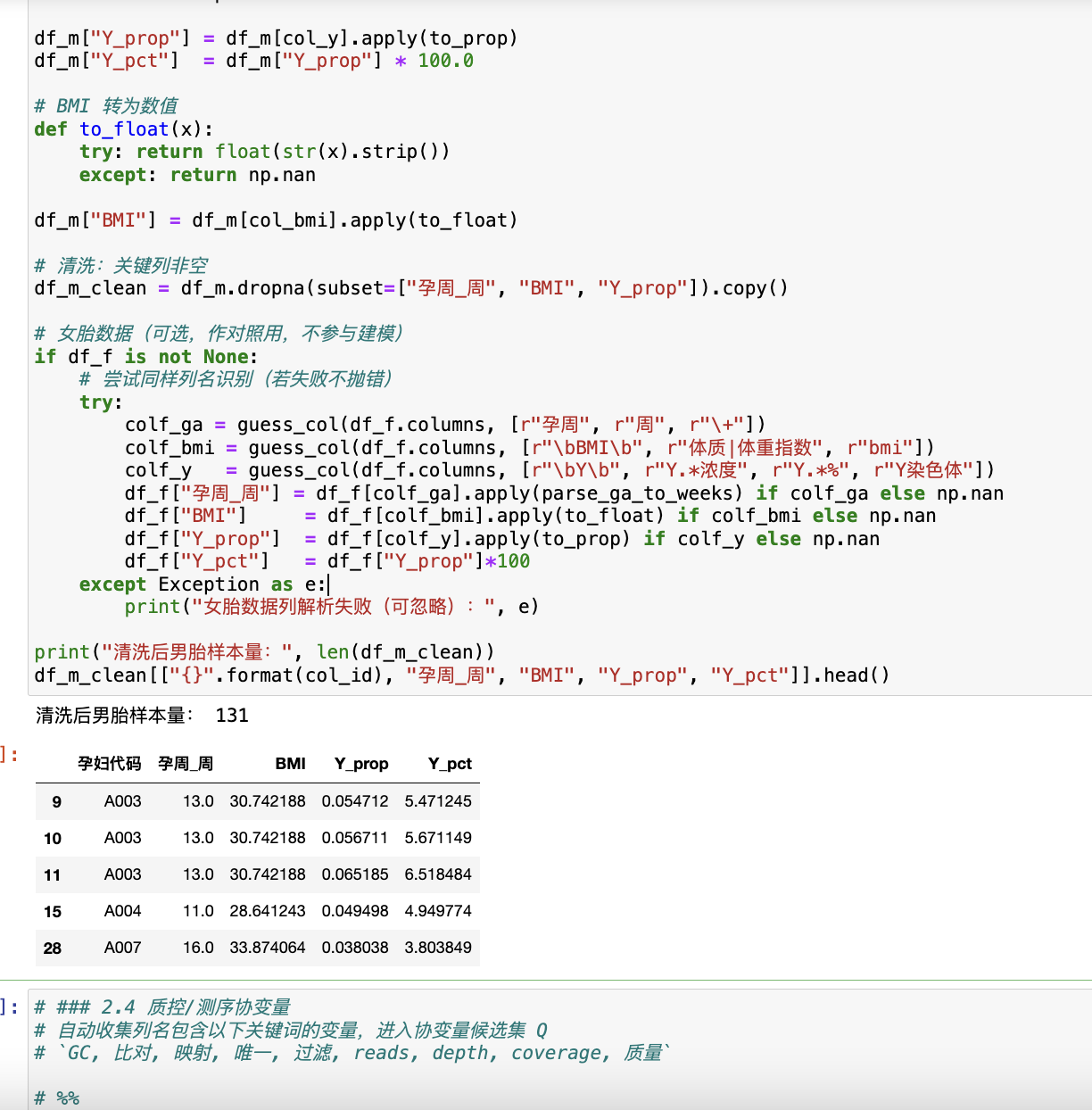
在本章中，我們以無創產前檢測（NIPT）數據為研究對象，圍繞“胎兒 Y 染色體濃度”(記為 (V)) 隨孕周 (G) 與 BMI (B) 的變化規律展開系統論證。為克服重復測量與個體差異帶來的估計偏倚，我們以混合效應模型為主線，以對數幾率變換與半參數平滑為兩翼，構建“LME / logit-LME / GAM”互證框架，并以極大似然推斷、懲罰樣條與交互效應檢驗為理論支撐。下文依次從問題表述與理論建模、數據預處理的數學化規范、模型構建與統計推斷、以及可視化與驗證四個層面展開，力求以嚴謹數學給出清晰可復核的證據鏈。

5.1 問題分析與理論建模

我們將每位受檢者記為 ，其于不同時點的觀測為 。其中 表示胎兒 Y 濃度（比例型變量）， 為以“周+天”折算的小數周， 為孕婦 BMI， 為測序/質控協變量向量（如 GC 含量、比對比例等）。同一受檢者可能存在多次檢測，數據天然具備“群組內相關性”。
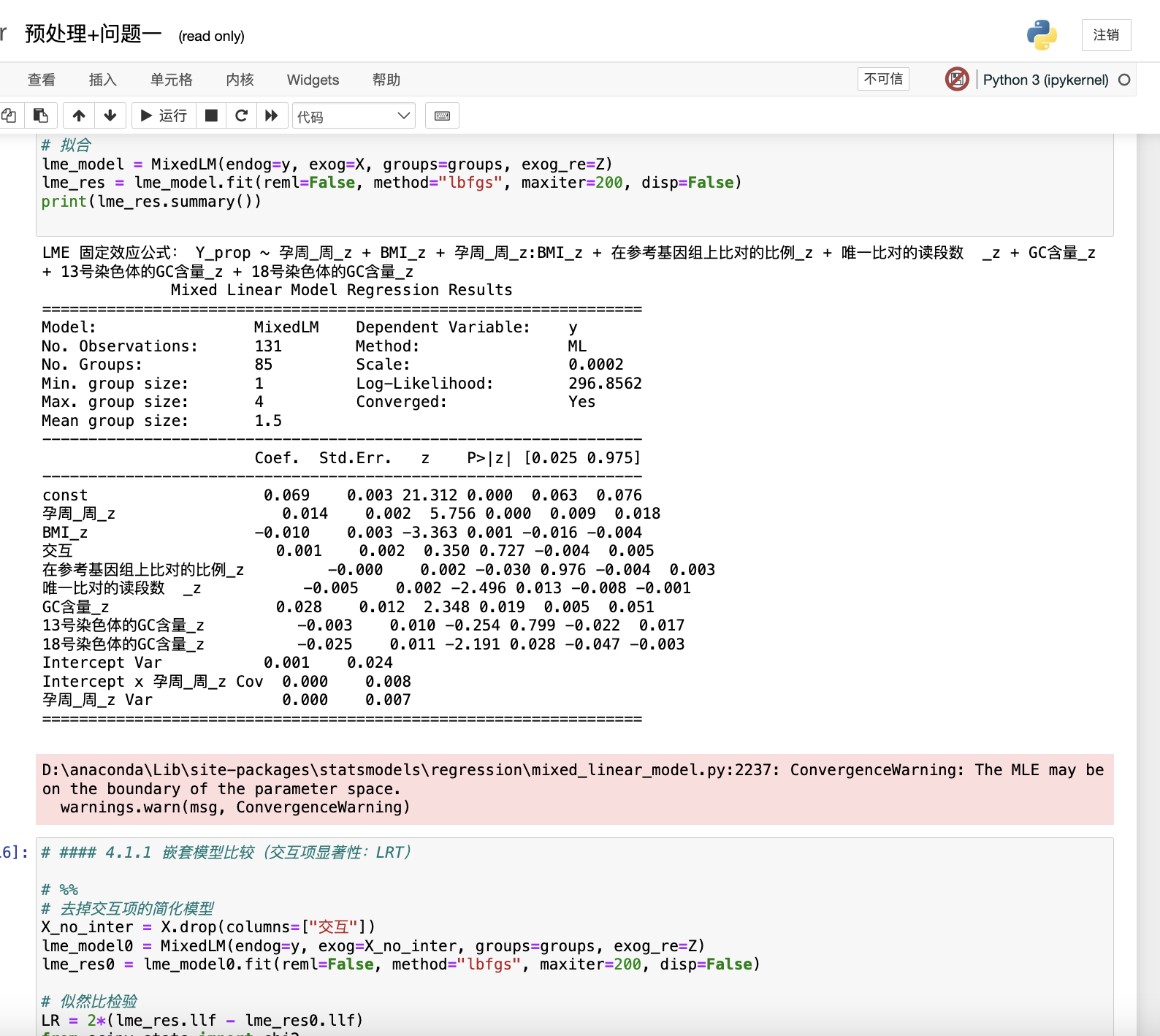
5.1.1 線性混合效應模型（LME）

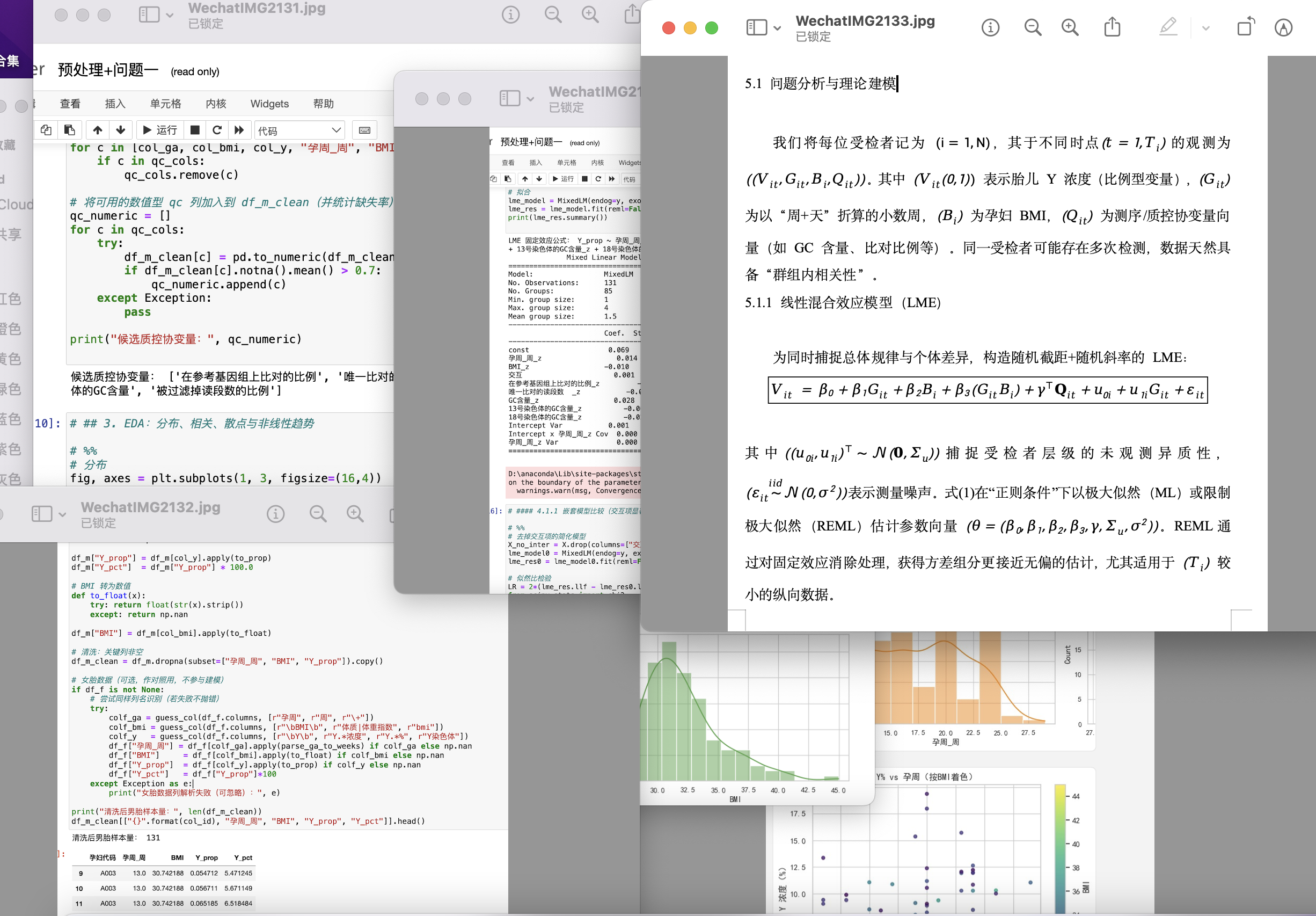
為同時捕捉總體規律與個體差異，構造隨機截距+隨機斜率的 LME：

其中捕捉受檢者層級的未觀測異質性，表示測量噪聲。式(1)在“正則條件”下以極大似然（ML）或限制極大似然（REML）估計參數向量 。REML通過對固定效應消除處理，獲得方差組分更接近無偏的估計，尤其適用于 較小的縱向數據。

推斷原理：在標準正則條件下， 漸近正態，

其中 為 Fisher 信息陣。據此對固定效應系數作 Wald 檢驗與區間估計；對模型嵌套關系（如是否需要交互項 或隨機斜率 ）可用似然比檢驗（LRT）：。

解釋幾何：式(1)給出條件均值（給定個體效應）下的線性面。其“簡單斜率”與“交互效應”可由偏導數表征：

若 ，則 BMI 改變孕周效應（與 有關的斜率），呈現“斜率非平行”的交互現象。

5.1.2 比例數據的 logit-LME（準 Beta 思路）

比例型響應常伴隨異方差與邊界效應。令 ，并取對數幾率變換 。構造與(1)同構的混合模型：

在對數幾率尺度上線性，回到原尺度的邊際預測為

閾值“等效孕周”：對某閾值 （如 4%），解方程：

據此可繪制“閾值等高線”，直觀呈現不同 BMI 下達到 的“等效孕周”。

5.1.3 廣義可加模型（GAM）與懲罰樣條

其目標函數為：

其中 為曲率懲罰， 由 GCV/REML 自適應選擇。