目錄
1.深度學習的介紹
2.神經網絡的構造
①神經元結構
②神經網絡組成
③權重核心性
3.神經網絡的本質
4.感知器
單層感知器的局限性:
5.多層感知器
多層感知器的優勢:
6.偏置
7.神經網絡的設計
8.損失函數
常用的損失函數:
9.softmax交叉熵損失函數
10.正則化懲罰
11.梯度下降
12.反向傳播
1.深度學習的介紹
深度學習(DL, Deep Learning)是機器學習(ML, Machine Learning)領域中一個新的研究方向。

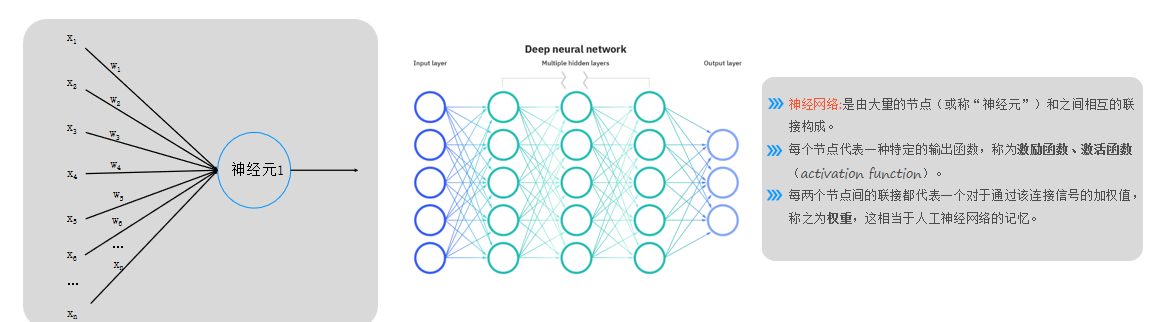
2.神經網絡的構造
①神經元結構
- 單個神經元模擬邏輯回歸,輸入信號(如圖片數據)通過權重(ω)加權求和后,經激活函數(如Sigmoid)輸出結果(0或1)。
- 輸入層(藍色)僅表示輸入數據,非神經元;輸出層(藍色末端)為最終結果。
②神經網絡組成
- 由大量神經元(節點)及連接線構成,每個節點代表一種特定的輸出函數,每層神經元按列排列,信號僅傳遞至下一層(無跨層或同層連接)。
- 激活函數(如Sigmoid)用于非線性映射,當前階段默認使用Sigmoid,后續會引入其他函數。
③權重核心性
- 權重(ω)是神經網絡的關鍵記憶單元,模型訓練的核心是求解權重值而非神經元本身。
3.神經網絡的本質
通過參數與激活函數來擬合特征與目標之間的真實函數關系。但在一個神經網絡的程序中,不需要神經元和線,本質上是矩陣的運算,實現一個神經網絡最需要的是線性代數庫。
4.感知器
有一層神經元組成的神經網絡叫做感知器,只能劃分線性數據

單層感知器的局限性:
- 單層感知器僅能處理線性分類問題(如用直線劃分數據),無法解決非線性分類(如圓形或復雜曲線分布的數據)。
5.多層感知器
增加了一個中間層,即隱含層(神經網絡可以做到非線性劃分的關鍵)????????
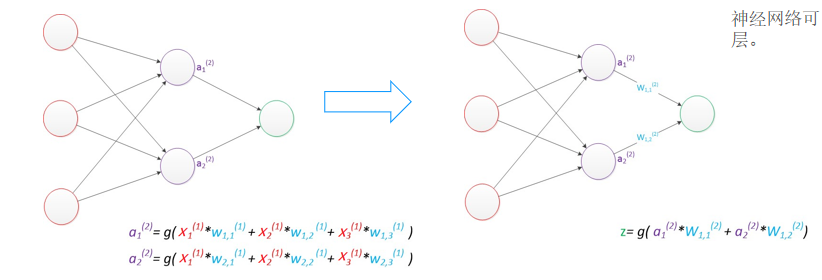
多層感知器的優勢:
- 引入隱含層后,通過多次非線性激活函數(如?
sigmoid)實現數據“彎曲”,從而處理非線性分類問題。 - 示例:
- 隱含層神經元數為1時,輸出為一條直線;
- 神經元數增至2或3時,可生成彎曲的決策邊界(如近似三角形或弧形),提升分類能力。
- 核心原理:前向傳播中,每層輸出經激活函數映射,疊加非線性特性。
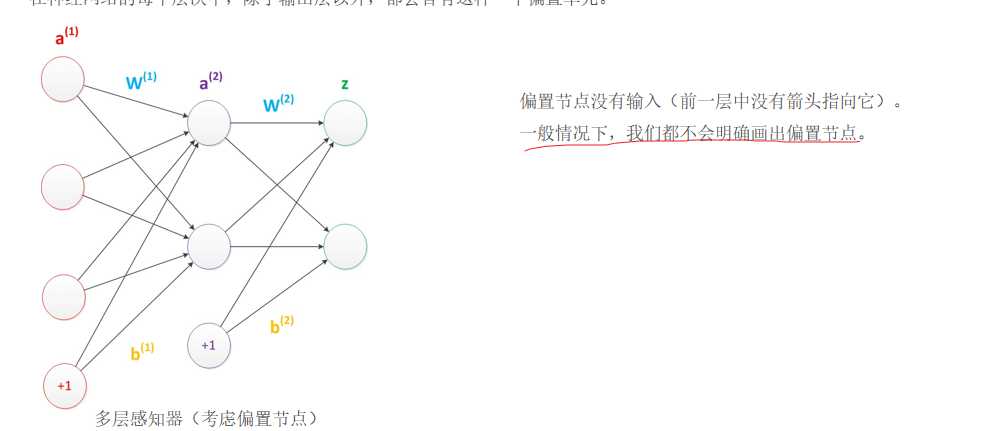
6.偏置
在神經網絡中需要默認添加偏置神經元(節點),它本質上是一個只含有存儲功能,且存儲值永遠為1的單元。 在神經網絡的每個層次中,除了輸出層以外,都會含有這樣一個偏置單元。
7.神經網絡的設計
輸入層的節點數:與特征的維度匹配
輸出層的節點數:與目標的維度匹配。
中間層的節點數:目前業界沒有完善的理論來指導這個決策。一般是根據經驗來設置。較好的方法就是預先設定幾個可選值,通過切換這幾個值來看整個模型的預測效果,選擇效果最好的值作為最終選擇。

8.損失函數
首先我們需要知道我們訓練模型的目的是使得參數盡可能的與真實的模型逼近。
具體做法:
1、首先給所有參數賦上隨機值。我們使用這些隨機生成的參數值,來預測訓練數據中的樣本。 2、計算預測值為yi,真實值為y。那么,定義一個損失值loss,損失值用于判斷預測的結果和真實值的誤差,誤差越小越好。
常用的損失函數:
0-1損失函數(二分類)
均方差損失
平均絕對差損失
交叉熵損失(分類)
合頁損失
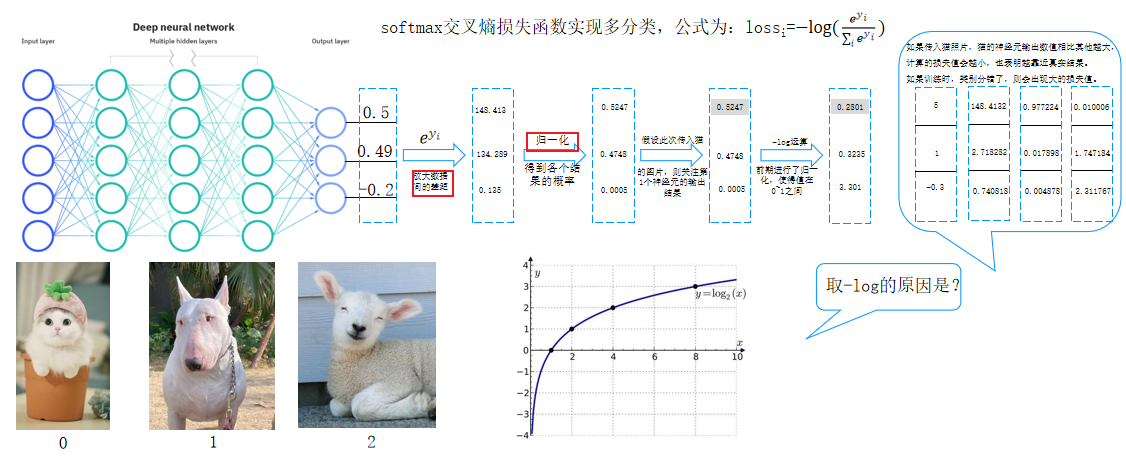
9.softmax交叉熵損失函數
softmax交叉熵損失函數實現多分類,公式為:lossi=?log?(e^y_i/∑_ie^y_i)????????
- 輸出層通過Softmax處理:
- 對神經元輸出值進行指數級放大(如e^{0.5}),拉大概率差異。
- 歸一化后得到各類別概率占比(總和為1)。
- 損失計算:
- 根據真實標簽選擇對應神經元的輸出概率。
- 通過負對數運算(-log(p))計算損失值:概率越接近1,損失越小;概率越低,損失越大。
- 多分類任務需對多張圖片的損失求平均值。
10.正則化懲罰
正則化懲罰的功能:主要用于懲罰權重參數w,一般有L1和L2正則化。
- 為防止過擬合和選擇更均衡的ω,損失函數需加入正則化項(如L1、L2正則化)。
- 正則化懲罰項的值隨ω的不均衡性增大而增大,促使模型選擇更均衡的參數
例如:
均方差損失函數:loss = 1/N∑_i=1^N(yp ? y)2+λR(W)
輸入為:x = [1,1,1,1]現有2種不同的權重值,
w1 = [1,0,0,0],w2 = [0.25,0.25,0.25,0.25]
w1和w2與輸入的乘積都為1,但w2 與每一個輸入數據進行計算后都有數據,使得w2會學習到每一個特征信息。而w1只和第1個輸入信息有關系,容易出現過擬合現象,因此w2的效果會比w1 好

11.梯度下降
梯度下降算法用于求解損失函數的極小值,通過計算損失函數對每個ω的偏導數確定下降方向
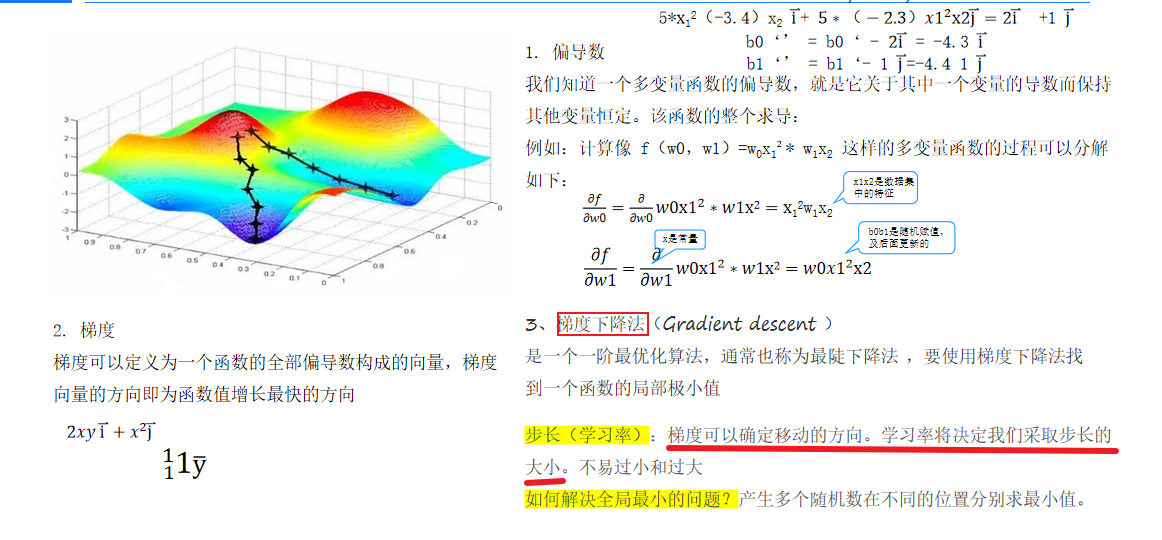
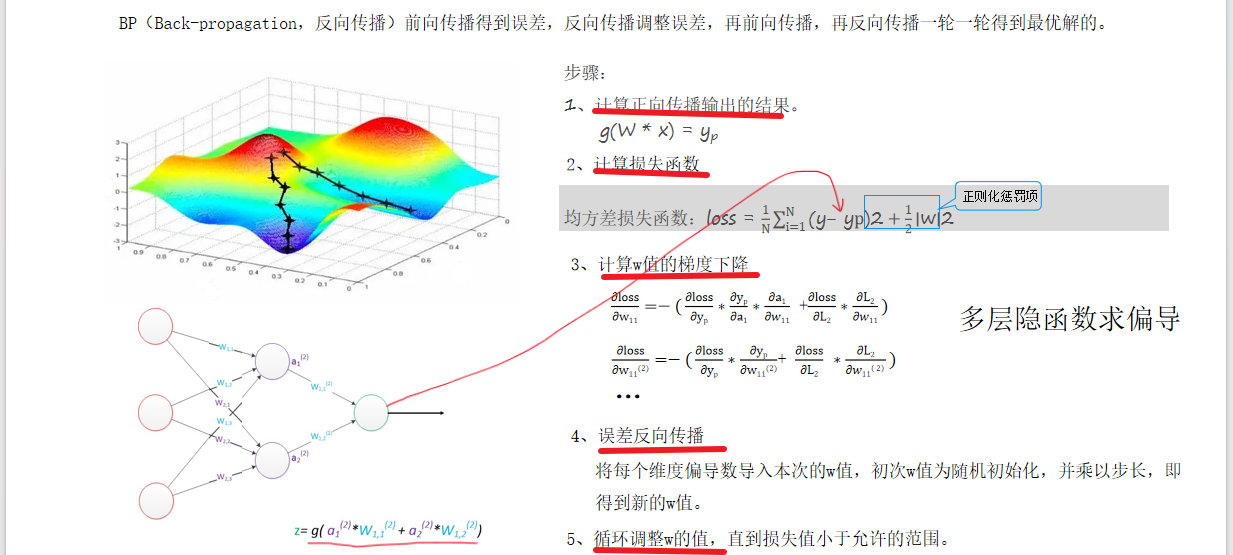
12.反向傳播
BP(Back-propagation,反向傳播)前向傳播得到誤差,反向傳播調整誤差,再前向傳播,再反向傳播一輪一輪得到最優解的。
- 反向傳播通過損失函數計算梯度,反向更新ω值,分為以下步驟:
- 隨機初始化ω。
- 前向傳播計算預測值(YP)和損失。
- 對每個ω求偏導(鏈式法則),代入當前ω值得到梯度方向。
- 根據學習率更新ω,迭代至收斂。
- 深層網絡中,偏導計算因隱函數嵌套變得復雜(如30層網絡需29次鏈式求導)。
)












)
)




與同義詞治理)