ICCV 2025 | Reverse Convolution and Its Applications to Image Restoration

在這里插入圖片描述

標題：Reverse Convolution and Its Applications to Image Restoration
作者：Xuhong Huang, Shiqi Liu, Kai Zhang, Ying Tai, Jian Yang, Hui Zeng, Lei Zhang
單位：Nanjing University, The Hong Kong Polytechnic University, OPPO Research Institute
論文：https://arxiv.org/abs/2508.09824
代碼：https://github.com/cszn/ConverseNet

convolution 和 transposed convolution 是神經網絡中廣泛使用的基礎算子。然而，transposed convolution（又稱 deconvolution）在數學形式上并非 convolution 的真正逆運算。迄今為止，尚未有 reverse convolution 算子被確立為神經架構的標準組件。
本文首次提出一種新穎的深度可分離 reverse convolution 算子，通過建立并求解正則化最小二乘優化問題，實現對 depthwise convolution 的有效反轉。我們全面研究了其核初始化、padding 策略等關鍵實現細節。
基于此算子，我們進一步構建 reverse convolution block，將其與 layer normalization、1×1 convolution 和 GELU 激活結合，形成類 Transformer 結構。所提出的算子與 block 可直接替換現有架構中的常規 convolution 和 transposed convolution 層，從而構建 ConverseNet。
針對典型圖像復原模型 DnCNN、SRResNet 和 USRNet，我們分別訓練三種 ConverseNet 變體，用于高斯去噪、超分辨率和去模糊。
大量實驗驗證了所提 reverse convolution 算子作為基礎構建模塊的有效性。我們希望這項工作能夠為深度模型設計中新算子的開發及其應用鋪平道路。

研究背景

卷積和轉置卷積（后面也稱為反卷積 deconvolution）是深度神經網絡中常用的基本操作。卷積用于特征提取并可以實現下采樣以減少空間維度。相反，轉置卷積廣泛用于對其輸入進行空間上采樣。這種功能關系導致一些研究將轉置卷積視為一種反向卷積形式。然而，從數學角度來看，轉置卷積不是卷積的真正逆運算；它可以通過在輸入元素之間插入零，然后進行標準卷積來描述。

與反卷積（deconvolution）相關的一個顯著方法是用于圖像去模糊的反卷積，它通過近似模糊過程的逆運算來從模糊圖像中恢復清晰圖像。然而，反卷積方法通常涉及迭代優化，并且通常專門用于去模糊，限制了其作為通用神經網絡模塊的靈活性。

另一個密切相關的工作是可逆卷積（invertible convolution），它通過施加特定約束（如相同的輸入輸出形狀和可處理的雅可比矩陣）來確保精確的可逆性。這些約束限制了其在深度網絡中的適用性。值得注意的是，可逆卷積本質上是標準卷積的約束形式，而不是一個全新的算子。因此，開發一個真正的反向卷積算子仍然是一個開放且有價值的研究方向。

盡管有效，這些方法通常會假定一個已知的模糊核操作在單通道灰度圖像或者三通道RGB圖像，這也限制了他們應用在深度網絡中的高維特征表征上的使用。盡管最近的深度Wiener Deconvolution可以應用到深度特征上，但是其主要針對于圖像去模糊。

因此，開發一個數學上嚴格、計算上高效、應用上廣泛的反向卷積（reverse convolution）算子具有重要的理論意義和實用價值。這種算子不僅能夠實現卷積的真正逆運算，還能夠在各種深度學習架構和任務中靈活應用，為深度模型設計提供新的思路和工具。

所以本文中，作者希望提出一種一次計算、無需迭代、支持任意通道維度、可直接嵌入現有網絡并真正反轉 depthwise convolution 的可學習算子。

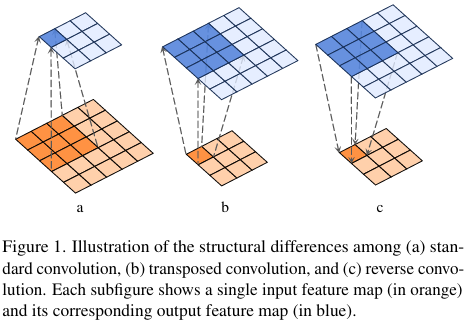
在這里插入圖片描述

研究內容

提出了一種深度可分離 reverse convolution 算子 Converse2D，用于 denoising、super-resolution、deblurring。

具體目標

給定 feature map $X∈RH×W\mathbf{X} \in \mathbb{R}^{H\times W}$ ，使用形狀為 $kh×kwk_h \times k_w$ 的depthwise卷積核 $K\mathbf{K}$ ，按照步長 $s$ 進行卷積后得到 $Y=(X?K)↓s\mathbf{Y} = (\mathbf{X} \otimes \mathbf{K}) \downarrow_s$ 。

目標是在已知 $Y,K,s\mathbf{Y}, \mathbf{K}, s$ 時，恢復 $X\mathbf{X}$ ，即 $X=F(Y,K,s)\mathbf{X} = \mathcal{F}(\mathbf{Y}, \mathbf{K}, s)$ 。

優化問題

如上恢復輸入的過程，可以看做是可以最小化重構輸出和實際輸出之間誤差的近似輸入。即最小化

$∥Y?(X?K)↓s∥F2+λ∥X?X0∥F2\|\mathbf{Y} - (\mathbf{X} \otimes \mathbf{K})\downarrow_s\|_F^2 + \lambda \|\mathbf{X} - \mathbf{X}_0\|_F^2$

$λ>0\lambda>0$ 為正則化參數，控制重構和正則化的權衡。在本文中，正則化參數可以在訓練過程中聯合優化，從而避免類似于現有大多數 deconvolution 算法中的手工調整
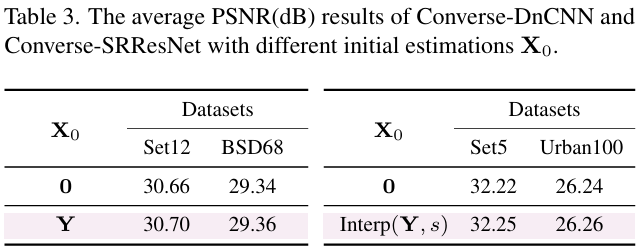
$X0\mathbf{X}_0$ 為初始估計，可以引導求解過程朝向更穩定和可信的結果，避免對于過擬合。

這里的 $λ∥X?X0∥F2\lambda \|\mathbf{X} - \mathbf{X}_0\|_F^2$ 是考慮到直接基于第一項的優化過程，由于退化恢復問題本身的病態特性可能導致的不穩定，而額外引入的正則化項。例如，跨步卷積的下采樣過程，恰好把高頻細節壓到 0，于是零空間包含大量高頻模式（即進過這種操作處理后會輸出0的輸入向量集合），從而從低分辨率輸出無法唯一確定高分辨率輸入，所以可以稱這個逆問題是“病態”的。所以通過引入額外的正則項，將實際的解限制在合理的初始解的附近，避免病態帶來的無意義的高頻噪聲。論文中引入了兩種簡單的初始估計 $X0=0\mathbf{X}_0 = \mathbf{0}$ 和 $X0=Interp(Y,s)\mathbf{X}_0 = \text{Interp}(\mathbf{Y}, s)$ ，后者表示對輸出的上采樣插值操作。

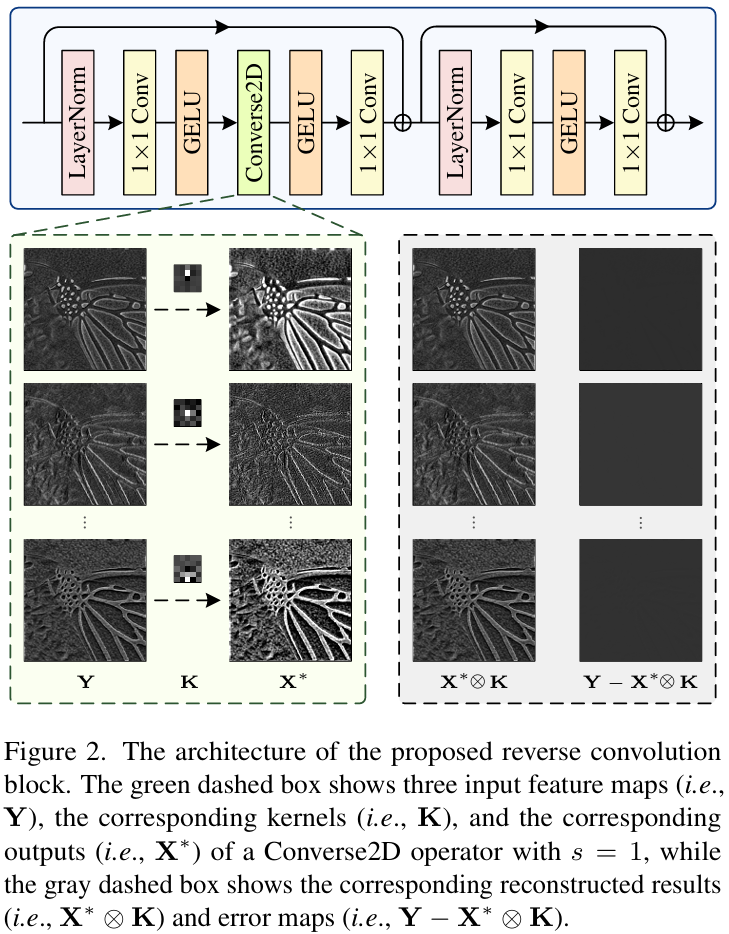
在這里插入圖片描述

求閉式解

這里采用了循環邊界假設（fast single image super-resolution using a new analytical solution for l2-l2 problems），即將二維特征圖在四個邊緣首尾相連后看做一個完整的環形圖像，例如上邊緣的上一行其實是原圖的最下面一行，左邊緣的左一列其實是原圖的最右面一列。在數學上，任意位置的像素都可以通過取模運算對應到圖像實際坐標上。這樣的處理方式，把卷積變成循環卷積（circular convolution），從而可用 FFT 在頻域一次性計算整幅圖，推導閉式解時能得到干凈的頻域公式。

整體的閉式解為

$X?=F?1(1λ(FK￣FY↑s+λFX0?L?FK￣⊙s(FKL)?s∣FK∣2?s+λ))\mathbf{X}^*=\mathbf{F}^{-1} \left(\frac{1}{\lambda} \left ( \underbrace{\overline{\mathbf{F}_K} \mathbf{F}_{Y \uparrow_s} + \lambda \mathbf{F}_{X_0}}_{\mathbf{L}} - \overline{\mathbf{F}_K} \odot_s \frac{(\mathbf{F}_K \mathbf{L}) \Downarrow_s}{| \mathbf{F}_K |^2 \Downarrow_s + \lambda } \right ) \right)$

$F(?)\mathbf{F}(\cdot)$ 表示 FFT， $F?1(?)\mathbf{F}^{-1}(\cdot)$ 表示正逆FFT
$∣Fk∣=Fk￣⊙Fk|\mathbf{F}_{k}|=\overline{\mathbf{F}_k} \odot \mathbf{F}_{k}$ ，即卷積核 $K\mathbf{K}$ 的傅里葉變換形式 $Fk\mathbf{F}_{k}$ 的復共軛和其自身之間的元素乘積，反映了平方幅度
$FY↑s\mathbf{F}_{Y \uparrow_s}$ 表示通過插入0值放大 $s$ 倍后特征的傅里葉變換
$⊙s\odot_s$ 表示在 $\times s$ 個不同塊上的元素乘法
$?s\Downarrow_s$ 為塊級別下采樣，即應用到 $\times s$ 個塊之間的平均操作
注意，該公式采用了 $↓s\downarrow_s$ 表示從 $\times s$ 塊中選擇左上角像素的下采樣形式的假設
當 $s = 1$ ，該公式簡化為 $X?=F?1(FK￣FY+λFX0∣FK∣2+λ)\mathbf{X}^*=\mathbf{F}^{-1} \left ( \frac{\overline{\mathbf{F}_K} \mathbf{F}_Y + \lambda \mathbf{F}_{X_0}}{| \mathbf{F}_K |^2 + \lambda } \right )$
這里的卷積核實際上可以聯合網絡學習，也可以以先驗的形式作為條件輸入

具體實現

為了實現Converse2D，這里介紹了幾個關鍵的組件細節：

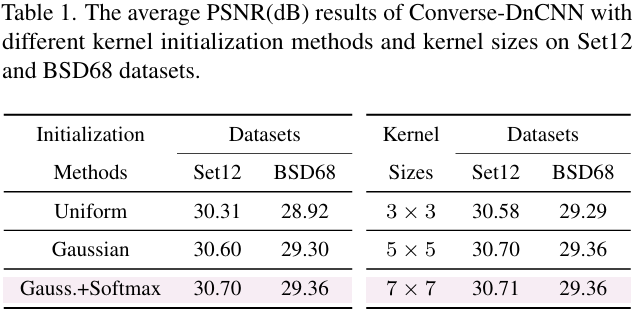
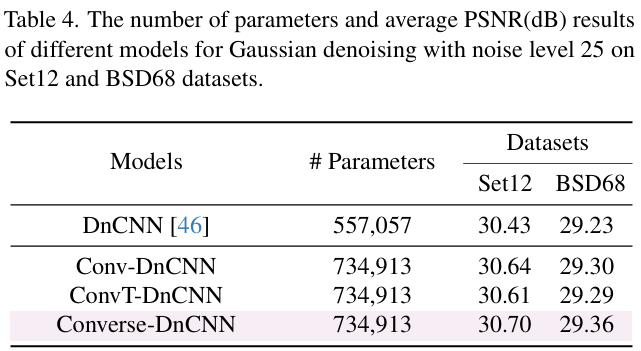
卷積核 $K\mathbf{K}$ ：初始化很重要，影響Converse2D生成的解的穩定性和準確性。受啟發于經典的去模糊方法，本文對隨機初始化的 $K\mathbf{K}$ 進一步應用 Softmax 歸一化，保證非負且和為 1。在高斯去噪任務上，這一方案效果優于均勻分布和高斯分布的初始化。同時實驗也展示了 $\times 5$ 大小的卷積核提供了更好的性能和效率的權衡。
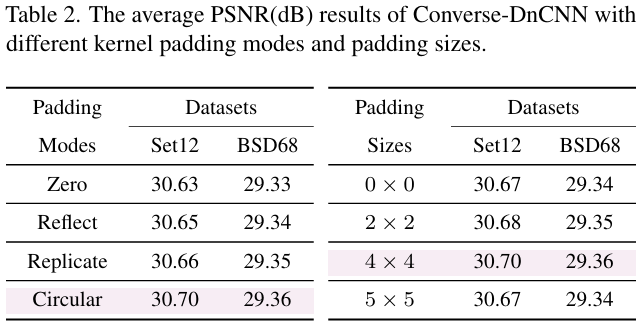
Padding策略：這回影響邊界信息的處理方式和輸出的空間尺寸。因此本文在提出的Converse2D上，分析了不同的padding模式（包括circular、reflect、replicate和zero padding）和尺寸。實驗中 padding size本身影響不大。circular padding 呈現了一致的優勢，這與現有去模糊的文獻中發現類似，因為circular padding可以更好的處理邊界并減少鋸齒。所以默認使用circular padding。
正則化參數：因為Converse2D本身是通道級別的應用形式，所以可以自然的為每個通道分配獨立的正則化參數來處理特征統計的變化，由于正則化參數本身也被集成到了Converse2D的計算中，所以可以自然地通過學習的方式來調整。這里使用了 $λ=Sigmoid(b?9.0)+?\lambda=\text{Sigmoid}(b-9.0)+\epsilon$ 的形式，其中 $e p s i l o n$ 是一個很小的常數來維持數值穩定。所有的可學習標量 $b$ 被初始化為0，并在訓練中自適應調整。而引入的偏移值“9”，則是用于產生一個較小的初始值，從而鼓勵訓練開始具有更強的數據保真度。
初始估計 $X0\mathbf{X}_0$ ：實驗對比反應了 Interp $(Y,s)(\mathbf{Y},s)$ 優于全零初始化，這是因為插值形式提供了一個更好的近似，而全零初始化導致更慢的收斂以及降低了恢復細微結構的能力。

基于算法偽代碼的大致實現如下：

import torch
import torch.nn.functional as F
import mathdef p2o(psf: torch.Tensor, out_shape):"""把空間核 (PSF)轉成頻域形式 (OTF)。卷積核之所以能被稱作 PSF（Point-Spread Function），是因為在圖像退化的線性系統里，卷積核恰好描述了“一個理想點光源經過該系統后所成的像”。psf: (B, C, kh, kw) PSF（Point-Spread Function） 就是空間域的卷積核 k，描述一個點光源經過系統后擴散成的“模糊斑”out_shape: (H*S, W*S) 目標高分辨率尺寸return: (B, C, H*S, W*S) OTF（Optical Transfer Function） 則是頻域的表示，等于 PSF 的傅里葉變換"""B, C, kh, kw = psf.shapeH, W = out_shape# 零填充到目標尺寸pad_h = H - khpad_w = W - kwpsf_pad = F.pad(psf, (0, pad_w, 0, pad_h))          # (B,C,H,W)# 循環移位，使核中心位于 (0,0)psf_pad = torch.roll(psf_pad, shifts=(-(kh//2), -(kw//2)), dims=(-2, -1))# 轉到頻域otf = torch.fft.fftn(psf_pad, dim=(-2, -1))return otfdef splits(x: torch.Tensor, s: int):"""把 tensor 切成 s×s 個塊x: (B, C, H*S, W*S)return: (B, C, H, W, s*s)"""B, C, HS, WS = x.shapeH = HS // sW = WS // sx = x.view(B, C, s, H, s, W)x = x.permute(0, 1, 3, 5, 2, 4).contiguous()x = x.view(B, C, H, W, s * s)return xdef sfold_upsampler(self, x: torch.Tensor, s: int):'''通過將元素復制到新的 sxs 局部區域的左上角來放大x: (B, C, H, W)return: (B, C, H*s, W*s)'''B, C, H, W = x.shapez = torch.zeros((B, C, H * s, W * s)).type_as(x)z[..., ::scale, ::scale].copy_(x)return zdef converse2d(X: torch.Tensor, K: torch.Tensor, S: int, bias: torch.Tensor) -> torch.Tensor:"""X: 輸入特征圖 (B, C, H, W)K: 卷積核 (B, C, kH, kW)S: 上采樣/下采樣比例bias: 可學習標量 (C,1,1) 用于生成 λreturn: 輸出特征圖 (B, C, H*S, W*S)"""B, C, H, W = X.shape# 1. 可學習的正則化參數 λlamb = torch.sigmoid(bias - 9.0) + 1e-5# 2. 最近鄰上采樣得到 X 的初始估計X_0 = F.interpolate(X, scale_factor=S, mode='nearest')# 3. 把輸入 X 通過插零放大Y_S = sfold_upsampler(X, S)# 4. 核轉到頻域 OTFFK = p2o(K, (H * S, W * S)) # (B,C,H*S,W*S) 復數FK_conj = torch.conj(FK) # 取共軛FK_2 = torch.abs(FK) ** 2 # 元素級 |FK|^2# 5. 頻域計算 L: B,C,H*S,W*SFKY = FK_conj * torch.fft.fftn(Y_S, dim=(-2, -1))L = FKY + torch.fft.fftn(lamb * X_0, dim=(-2, -1))# 6. 計算 FKL 與 FK2 的塊均值FKL_S = splits(FK * L, S).mean(dim=-1) # (B,C,H,W)FK2_S = splits(FK_2, S).mean(dim=-1)# 7. 頻域除法Fdiv = FKL_S / (FK2_S + lamb)# 8. 通過對整體的重復來恢復 Fdiv 到高分辨率Fmul = FK_conj * Fdiv.repeat(1, 1, S, S) # (B,C,H,W) -> (B,C,H*S,W*S)Fout = (L - Fmul) / lamb# 9. 逆 FFT 取實部out = torch.fft.ifftn(Fout, dim=(-2, -1)).realreturn out

模型細節

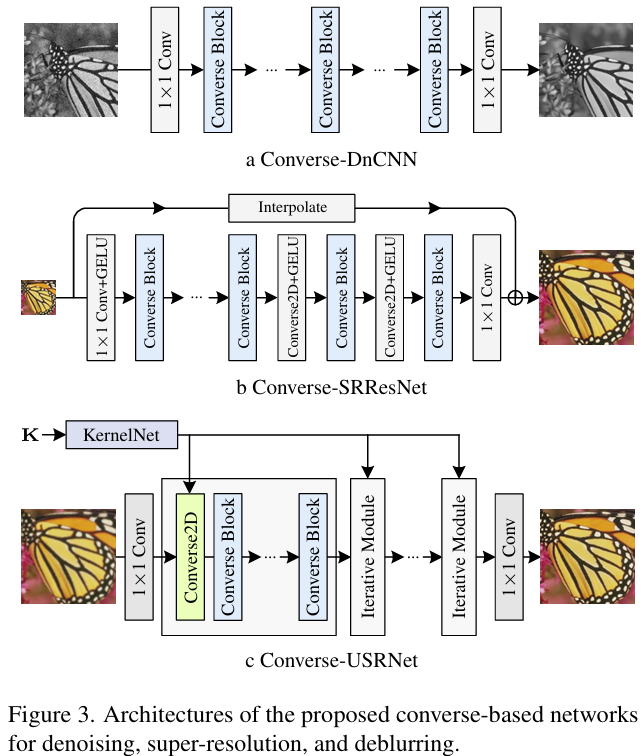
在這里插入圖片描述

本文基于提出的 Converse2D，構建了Reverse Convolution Block，其中包含 LayerNorm、1×1 Conv、GELU、Converse2D（深度分離的形式）、殘差連接，內部實現空間（主要由Converse2D負責）與通道（主要由1x1卷積處理）分離建模。

Converse-DnCNN和Converse-SRResNet均直接替換各自的核心構建塊為Converse2D算子模塊
Converse-USRNet則是用于展示所提算子在kernel-conditioned的場景中的表現，即非盲去模糊任務。將 USRNet 的 data module 換成 Converse2D、并替換其中的ResUNet denoiser為ConverseNet，這包含了7個Converse Block。也設計了 KernelNet 將模糊核映射到 64 維嵌入，這可以直接用于參數化 Converse2D，只有正則化參數是可學習的。

研究價值

首次給出 depthwise convolution 的嚴格可逆算子，一次前向完成反演；可直接替換現有卷積/轉置卷積層，無需迭代；支持任意通道維度，可在特征域而非圖像域完成 non-blind deblurring；實驗顯示在 denoising、super-resolution、deblurring 上均優于或與原結構持平，具有通用模塊潛力。

要點匯總

Converse2D 算子通過正則化最小二乘問題的閉式解實現了 depthwise convolution 的真正可逆運算 頻域推導給出一次性前向計算公式，無需迭代，可直接嵌入深度網絡（見“Closed-form Solution”）。
Converse2D 支持任意通道維度，可在高維特征空間完成 deblurring，突破傳統 deconvolution 僅限 1、3 通道圖像的限制 文中指出“unlike deconvolution methods … our operator … supports arbitrary channel dimensions, enabling broad adaptability across network architectures”（見 Abstract 和 Sec. 3）。
Converse Block 采用 Transformer-like 結構，將空間建模（Converse2D）與通道交互（1×1 Conv）解耦，提高模塊化與表達能力 “separation of spatial and channel-wise processing makes the Converse block an effective and flexible module”（見 Sec. 3.4）。
Softmax 歸一化的核初始化、Circular padding、插值初始估計 $X0\mathbf{X}_0$ 與可學習正則化參數 $λ\lambda$ 是 Converse2D 穩定訓練與性能提升的關鍵 實驗表格顯示 Softmax 初始化 PSNR 高于 Uniform/Gaussian；Circular padding 優于其他模式；Interp $(Y,s)(\mathbf{Y},s)$ 初始化優于全零（見 Sec. 4 和表 1–3）。

在這里插入圖片描述

在 Gaussian denoising 任務上，Converse-DnCNN 在 Set12 和 BSD68 數據集上以相同噪聲水平 σ=25 取得更高 PSNR，驗證算子有效性 表 4 顯示 Converse-DnCNN 在 BSD68 達 29.36 dB，高于 Conv-DnCNN 與 ConvT-DnCNN。
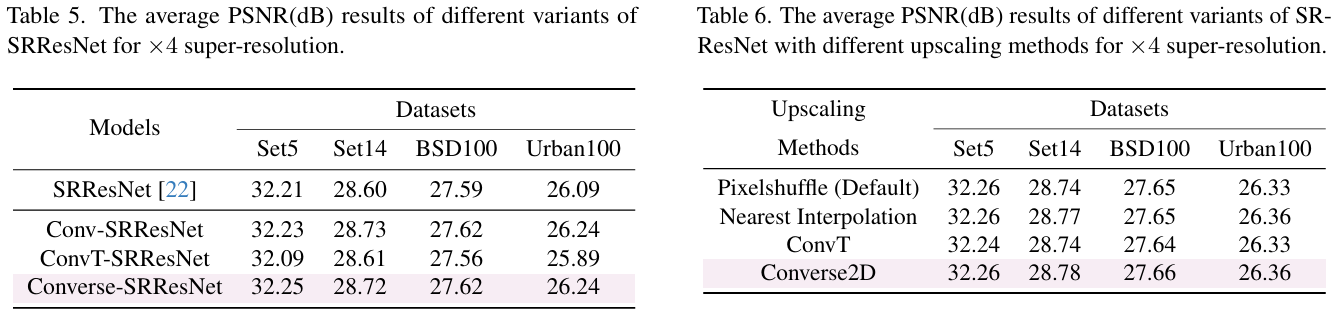
在 ×4 super-resolution 任務上，Converse-SRResNet 與 SRResNet、Conv-SRResNet、ConvT-SRResNet 性能持平，證明 Converse2D 可直接替換轉置卷積而不損失精度 表 5 給出各模型在 Set5/Set14/BSD100/Urban100 的 PSNR 對比。
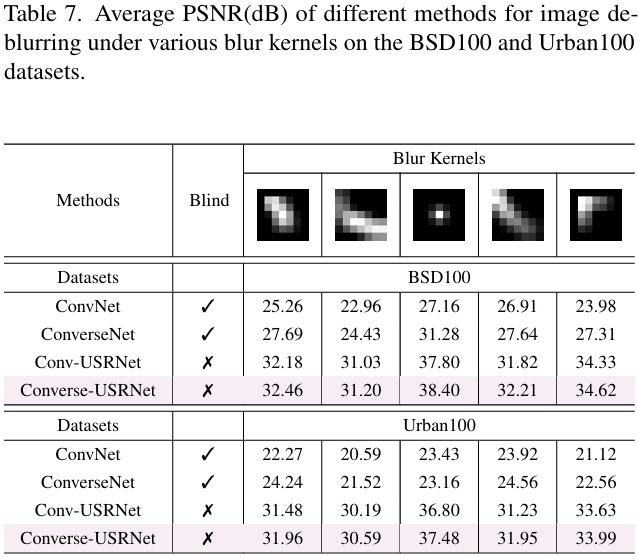
在非盲 deblurring 場景下，Converse-USRNet 通過 KernelNet 將模糊核嵌入特征域，PSNR 高于 Conv-USRNet，并減少邊界偽影 表 7 和圖 6 對比顯示 Converse-USRNet 在 BSD100/Urban100 上優于 Conv-USRNet，且“generate well-aligned and visually sharp outputs”。
在盲 deblurring 設置下，ConverseNet 仍優于 ConvNet，說明 Converse2D 本身具備去卷積能力，可減輕幾何失真 （見 Sec. 5.3）。