LeetCode 654. 最大二叉樹，【難度：中等；通過率：82.6%】，這道題的描述本身就是一份遞歸的構造方式，我們的任務就是將這份描述優雅地 翻譯成代碼；且思路類似 “由中序與前序/后序遍歷結果構建二叉樹”，參考：

• leetcode105深度解析：從前序與中序遍歷序列構造二叉樹
• leetcode106深度解析：從中序與后序遍歷序列構造二叉樹

一、 題目描述

給定一個不含重復元素的整數數組 nums。一個以此數組直接遞歸構建的 最大二叉樹 定義如下：

1. 二叉樹的根是數組 nums 中的最大元素
2. 左子樹是通過數組中 最大值左邊部分 遞歸構造出的最大二叉樹
3. 右子樹是通過數組中 最大值右邊部分 遞歸構造出的最大二叉樹

返回由 nums 構建的 最大二叉樹

示例:

示例 1:

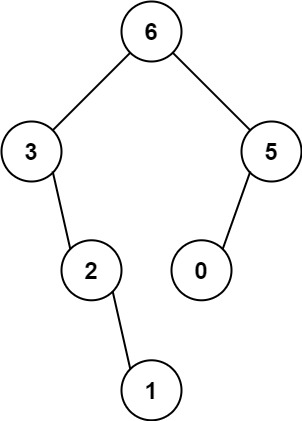
輸入: nums = [3,2,1,6,0,5]
輸出: [6,3,5,null,2,0,null,null,1]
解釋:
根節點是數組 [3,2,1,6,0,5] 中的最大值 6
左子樹是數組 [3,2,1] 構建出的最大二叉樹
右子樹是數組 [0,5] 構建出的最大二叉樹

示例 2:

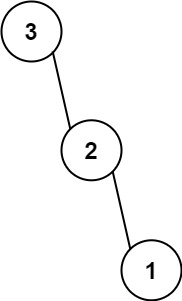
輸入: nums = [3,2,1]
輸出: [3,null,2,null,1]

---

二、 核心思路：分而治之與遞歸構造

題目的定義已經為我們指明了道路——遞歸。構建整棵樹的過程，和構建其任意子樹的過程，遵循著完全相同的規則，只是處理的數組范圍不同。這就是典型的“分而治之”思想

我們可以將構建過程分解為三步：

1. 找到根節點：在當前需要處理的數組范圍內，找到最大值及其索引。這個最大值就是當前子樹的根節點
2. 構建左子樹：對最大值左邊的子數組，遞歸地執行相同的構建過程，并將返回的根節點作為當前根節點的左孩子
3. 構建右子樹：對最大值右邊的子數組，遞歸地執行相同的構建過程，并將返回的根節點作為當前根節點的右孩子

這個過程會一直持續下去，直到需要處理的子數組為空，此時返回 null，遞歸終止

三、代碼實現與深度解析

直觀解法就是定義一個輔助遞歸函數，該函數接收數組和需要處理的索引范圍 [left, right] 作為參數

class Solution {public TreeNode constructMaximumBinaryTree(int[] nums) {// 調用輔助遞歸函數，初始范圍為整個數組return build(nums, 0, nums.length - 1);}/*** 輔助遞歸函數：在指定的數組范圍 [left, right] 內構建最大二叉樹* @param nums  原始數組* @param left  當前處理范圍的左邊界（包含）* @param right 當前處理范圍的右邊界（包含）* @return 構建好的子樹的根節點*/private TreeNode build(int[] nums, int left, int right) {// 步驟 1: 定義遞歸終止條件// 如果左邊界大于右邊界，說明當前范圍為空，無法構建節點if (left > right) {return null;}// 步驟 2: 在當前范圍 [left, right] 內找到最大值的索引int maxIndex = -1;int maxValue = Integer.MIN_VALUE;for (int i = left; i <= right; i++) {if (nums[i] > maxValue) {maxValue = nums[i];maxIndex = i;}}// 步驟 3: 創建根節點TreeNode root = new TreeNode(maxValue);// 步驟 4: 遞歸構建左子樹// 左子樹的范圍是 [left, maxIndex - 1]root.left = build(nums, left, maxIndex - 1);// 步驟 5: 遞歸構建右子樹// 右子樹的范圍是 [maxIndex + 1, right]root.right = build(nums, maxIndex + 1, right);// 步驟 6: 返回當前構建好的根節點return root;}
}

---

四、 關鍵點與復雜度分析

• 遞歸函數的定義：build(nums, left, right) 的定義非常關鍵。它清晰地界定了每次遞歸需要處理的子問題——在 nums 數組的 [left, right] 區間內構建最大二叉樹
• 尋找最大值：在每個遞歸步驟中，核心操作都是遍歷當前子數組以找到最大值。這是主要的耗時部分
• 時間復雜度：在最壞的情況下（例如，數組是升序或降序排列的），樹會退化成一個鏈表。每次尋找最大值的操作都需要掃描近乎整個子數組，總的時間復雜度為 O(N) + O(N-1) + … + O(1) = O(N2)
• 空間復雜度：空間開銷主要來自遞歸調用棧。棧的深度取決于樹的高度 H。在最壞情況下（退化為鏈表），樹的高度為 N，因此空間復雜度為 O(N)。在平均情況下（樹比較平衡），高度為 O(log N)，空間復雜度為 O(log N)

---

五、拓展解法

這道題的樸素遞歸解法時間復雜度是 O(N2)，有沒有優化的可能呢？

答案是肯定的。瓶頸在于每次都需要線性掃描來尋找最大值。如果我們能用更高效的方式在數組的一個區間內找到最大值，就能優化性能。例如，使用單調棧可以在 O(N) 的時間內完成整個構建過程。但這需要更復雜的邏輯，因為它將樹的構建過程從 “遞歸分解” 變為了 “迭代構建”，參考代碼如下：

單調棧解法

class Solution {public TreeNode constructMaximumBinaryTree(int[] nums) {if (nums == null || nums.length == 0) {return null;}// 使用數組（刷題環境顯然需要追求極致性能，別用Stack）模擬棧// 存儲 TreeNode 引用// 棧的大小最大為 nums.lengthTreeNode[] stack = new TreeNode[nums.length];int top = -1; // 棧頂指針，初始化為 -1 表示棧空for (int num : nums) {TreeNode node = new TreeNode(num); // 創建當前節點// 步驟 1: 處理棧頂元素 (pop)// 如果棧不為空，且棧頂元素的值小于當前節點的值// 那么棧頂元素應該成為當前節點的左孩子while (top != -1 && stack[top].val < node.val) {node.left = stack[top]; // 棧頂元素成為當前節點的左孩子top--; // 彈出棧頂元素}// 步驟 2: 連接當前節點的右孩子 (peek)// 如果棧不為空，且棧頂元素的值大于當前節點的值// 那么當前節點應該成為棧頂元素的右孩子if (top != -1) {stack[top].right = node; // 當前節點成為棧頂元素的右孩子}// 步驟 3: 當前節點入棧 (push)top++;stack[top] = node;}// 循環結束后，棧底（即 stack[0]）的元素就是整棵樹的根節點// 因為它是最后一個入棧的，且沒有比它更大的元素讓它彈出或成為右孩子return stack[0]; }
}

兩種解法對比

	遞歸構建 (樸素、直觀解法)	單調棧 (O(N) 優化解法)
核心思路	分而治之：找到當前范圍最大值作為根，遞歸處理左右子數組	利用結構：通過維護一個單調遞減棧，一次遍歷確定每個節點的左右孩子
構建過程	1. 遍歷當前子數組找最大值 2. 創建根節點 3. 遞歸構建左子樹 4. 遞歸構建右子樹	1. 遍歷數組元素，創建節點 curr 2. 棧頂小于 curr，彈出并作為 curr 的左孩子 3. 棧頂大于 curr，curr 作為棧頂的右孩子 4. curr 入棧
時間復雜度	O(N2)：每次遞歸都可能線性掃描子數組找最大值	O(N)：每個元素最多入棧一次、出棧一次，哈希表操作平均 O(1)
空間復雜度	O(N)：遞歸棧深度最壞為 N (退化為鏈表)	O(N)：棧中最多存儲 N 個節點 (最壞情況)
代碼可讀性	高：與題目定義高度吻合，直觀易懂	中等/低：邏輯較為抽象，需要理解單調棧的特性和指針連接規則
理解難度	較低，適合初學者入門遞歸	較高，需要對棧、樹結構和相對大小關系有深入理解
底層實現	遞歸函數調用棧	通常使用數組 或 Deque (如 ArrayDeque) 模擬棧；不建議使用Stack
缺點	效率低，可能導致超時	邏輯復雜，不易一次性寫對