接上篇
重溫無功功率測量-CSDN博客
已知被測阻抗兩端電壓與流過 通過兩個ADC同步采集到。
激勵頻率10k, 采樣率1M, 每周期100個點
關鍵是:采樣率除以激勵頻率, 得是4的倍數... 所以ADC不能自由運行, 得用一個timer來觸發.
因為要進行同相分量正交分量計算。
1:直流分量計算
int buf_size = sizeof(pdc->data.adc_buf) / sizeof(pdc->data.adc_buf[0]);for(int i = 0; i < buf_size; i++) {mean_v += pbuf[i].v;mean_i += pbuf[i].i;}mean_v /= buf_size;mean_i /= buf_size; // 求平均值, 用于直流平衡2:計算相位
for(int i = 50; i < buf_size - 50; i++) {prod_i += -(pbuf[i].v - mean_v) * (pbuf[i].i - mean_i); // v和i做直流平衡后相乘, 累加得到同相分量prod_q += (pbuf[i + 25].v - mean_v) * (pbuf[i].i - mean_i); // 激勵頻率10k, 采樣率1M, 每周期100個點, 因此移動25個點再平衡, 相乘, 累加就是正交分量了}prod_i /= buf_size;prod_q /= buf_size;phase = atan2(prod_q, prod_i); // 同相分量和正交分量, atan2即得到相位差原理解釋
使用
atan2函數和同相、正交分量的平均值,確實可以得到相位角。 這也是一種在數字信號處理中非常常用和穩健的相位計算方法。原理簡述
首先,讓我們理解什么是同相分量和正交分量。
假設你有一個信號 s(t)=Acos(ωt+?),它的同相分量 (In-phase, I) 和正交分量 (Quadrature, Q) 可以通過將其與參考信號(通常是 cos(ωt) 和 ?sin(ωt) 或 sin(ωt))相乘,并取其在周期內的平均值來得到。
同相分量 (I): 表示信號在參考信號 cos(ωt) 上的投影。它與信號的幅度和相位有關。
正交分量 (Q): 表示信號在參考信號 sin(ωt) 上的投影。它也與信號的幅度和相位有關。
通過積分或求平均值,我們可以得到:
I=T1?∫0T?s(t)cos(ωt)dt=2A?cos(?)
Q=T1?∫0T?s(t)sin(ωt)dt=2A?sin(?)
注意:在數字信號處理中,積分會變成求和。
為什么
atan2(Q, I)有效?根據上面的公式,我們可以看到:
IQ?=2A?cos(?)2A?sin(?)?=cos(?)sin(?)?=tan(?)
所以,?=arctan(IQ?)。
但是,
arctan(y/x)有一個問題:它只能輸出 ?π/2 到 π/2 之間的角度,無法區分第一、三象限和第二、四象限的角度。
atan2(y, x)函數解決了這個問題。它通過同時使用 y (這里的 Q) 和 x (這里的 I) 的正負號信息,來確定相位角所在的完整 2π 范圍,即 ?π 到 π。
如果 I>0,Q>0,相位角在第一象限。
如果 I<0,Q>0,相位角在第二象限。
如果 I<0,Q<0,相位角在第三象限。
如果 I>0,Q<0,相位角在第四象限。
因此,
atan2(Q, I)能夠精確地計算出信號的相位角,而不會產生象限模糊。步驟
選擇基準頻率:確定你要分析的信號的基波頻率 f0?,并生成兩個正交的參考信號:cos(2πf0?t) 和 sin(2πf0?t)。
計算同相分量 (I):將你的原始采樣信號與 cos(2πf0?t) 相乘,并對結果求平均值(或在一個周期內求和)。
計算正交分量 (Q):將你的原始采樣信號與 sin(2πf0?t) 相乘,并對結果求平均值(或在一個周期內求和)。
計算相位角:將得到的 Q 和 I 值代入
atan2函數:相位角=atan2(Q,I)
這個方法等同于對信號進行離散傅里葉變換 (DFT),然后取基波頻率處的實部和虛部。同相分量 I 對應于傅里葉變換的實部,正交分量 Q 對應于傅里葉變換的虛部。因此,這是一種非常可靠且常用的方法。
這種方法通常被稱為 I/Q 解調 (In-phase and Quadrature Demodulation) 或 正交解調。
在數字信號處理中,I/Q 是同相 (In-phase) 和正交 (Quadrature) 的縮寫。通過將信號分別與一對正交的參考信號(例如 cos(ωt) 和 sin(ωt))相乘并求平均,我們可以提取出信號的 I 分量和 Q 分量。
I 分量 對應于信號的實部。
Q 分量 對應于信號的虛部。
這兩個分量共同構成了一個復數,這個復數包含了信號的幅度和相位信息。而
atan2(Q, I)函數正是用來從這個復數中計算出精確的相位角。因此,這個方法在很多領域都有廣泛應用,尤其是在通信、雷達和各種數字信號處理系統中,用來對信號進行解調、分析和處理。
3:計算阻抗模
for(int i = 50; i < buf_size - 50; i++) {rms_sq_sum_v += pow((pbuf[i].v - mean_v),2); rms_sq_sum_i += pow((pbuf[i].i - mean_i),2);}float U_rms = sqrt(rms_sq_sum_v / buf_size);float I_rms = sqrt(rms_sq_sum_i / buf_size);float Z_modulus = U_rms / I_rms;原理解釋?
第1步:計算電壓的有效值 (U_rms)
有效值(方均根值)代表了交流信號的等效能量。它的計算方法是:
對每個電壓采樣點進行平方。
將所有平方值相加求和。
將求和結果除以采樣點數 (1000)。
對最終結果開方。
第2步:計算電流的有效值 (I_rms)
使用同樣的方法計算電流的有效值:
對每個電流采樣點進行平方。
將所有平方值相加求和。
將求和結果除以采樣點數 (1000)。
對最終結果開方。
第3步:計算阻抗的模 (∣Z∣)
阻抗的模等于電壓的有效值除以電流的有效值。
∣Z∣=Urms??/Irms?
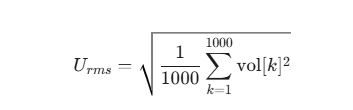
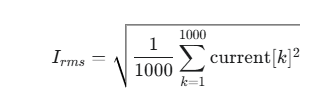



![Agents-SDK智能體開發[4]之集成MCP入門](http://pic.xiahunao.cn/Agents-SDK智能體開發[4]之集成MCP入門)















