03 基于sklearn的機械學習-線性回歸、損失函數及其推導

線性回歸

分類的目標變量是標稱型數據，回歸是對連續型的數據做出預測。

一、標稱型數據（Nominal Data）

標稱型數據屬于分類數據（Categorical Data） 的一種，用于描述事物的類別或屬性，沒有順序或數值意義，僅用于區分不同的組別。

核心特征

離散性：數據值是有限的、離散的類別，無法進行數學運算（如加減乘除）。
無順序性：類別之間沒有高低、大小或先后順序，彼此平等。
標簽化：通常用字符串或整數標簽表示（如 “紅色”“藍色”，或用 0、1、2 代表不同類別），但標簽的數值不具備實際意義。

常見例子

性別：男 / 女
顏色：紅 / 黃 / 藍
職業：教師 / 醫生 / 工程師
學歷：高中 / 本科 / 碩士（注意：學歷若僅作為類別則是標稱型，若強調順序則是有序型數據，屬于分類數據的另一種）

二、連續型數據（Continuous Data）

連續型數據是可以取無限多個數值的定量數據，通常用于衡量事物的數量或程度，具有數值意義和順序性。

連續型數據可直接參與數值計算，但為了提升模型效果，通常需要預處理：標準化/歸一化/離散化

核心特征

連續性：在一定范圍內可以取任意值（理論上可無限細分），如身高 175cm、體重 62.5kg 等。
可運算性：支持加減乘除等數學運算，且結果有實際意義（如身高差、體重和）。
有序性：數值之間有明確的大小關系（如 180cm > 170cm）。

常見例子

物理量：身高、體重、溫度、時間
統計量：收入、成績、點擊率、年齡（嚴格來說年齡可視為離散型，但通常按連續型處理）

線性回歸

線性回歸（Linear Regression）是監督學習中最基礎的算法之一，用于建模自變量（特征或者X）與因變量（目標，y）之間的線性關系。

需要預測的值:即目標變量,target,y

影響目標變量的因素: $X_1,X_2...X_n$ ,可以是連續值也可以是離散值

因變量和自變量之間的關系:即模型,model

對于數學中的線性回歸通常為數學公式，例如y=w**x+b，是完全對的，但是在現實生活中，預測的結果與實際結果不完全一致，因此機器學習中的線性回歸的目的是通過擬合一條直線，使預測值盡可能地接近真實值。

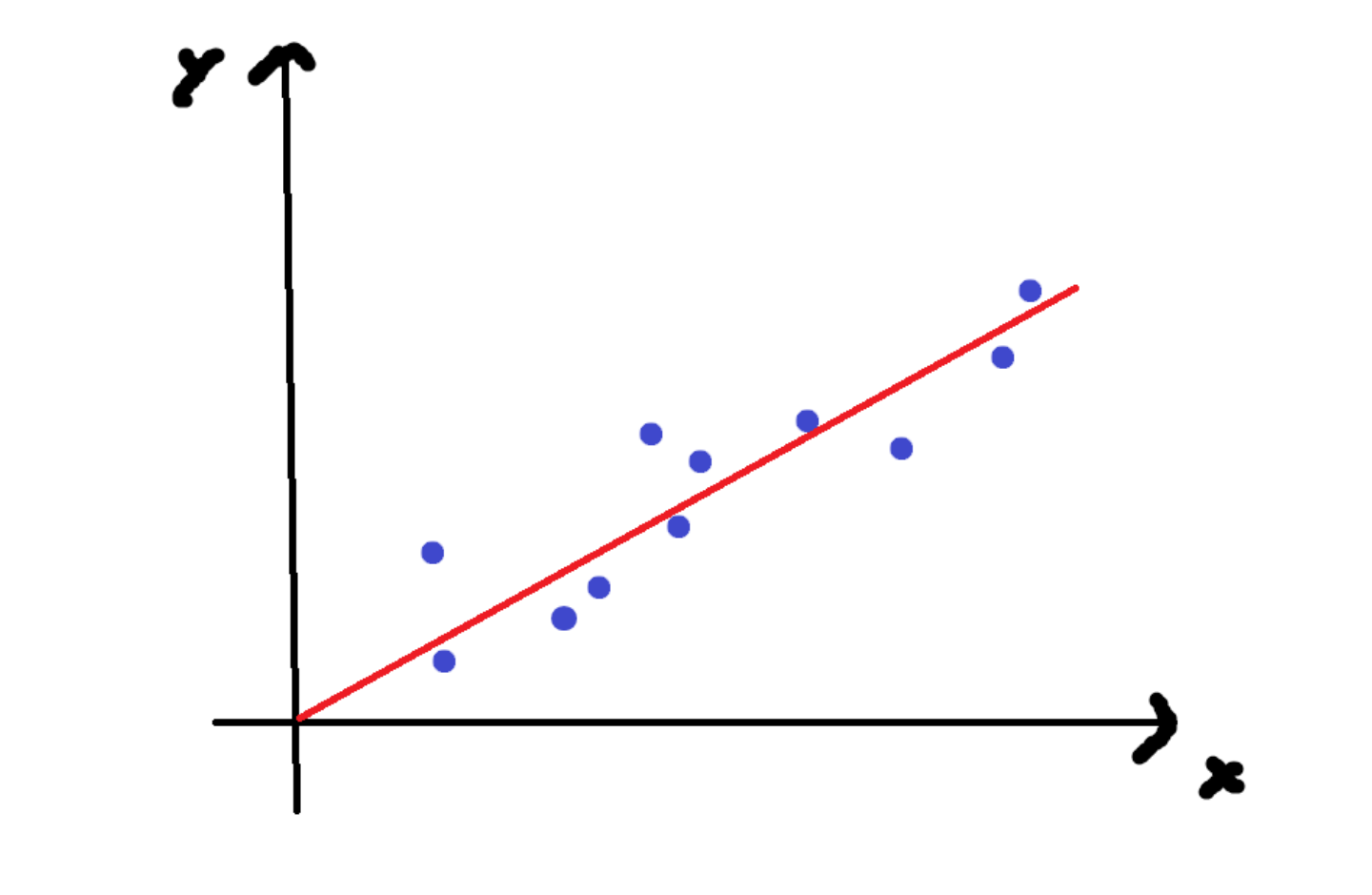
在這里插入圖片描述

損失函數

損失函數（Loss Function）是衡量模型預測錯誤程度的函數，定義為預測值與真實值之間的差異。

假設: $y = w x + b$

把 $x_1,x_2,x_3...$ 帶入進去然后得出:

$y_1^,=wx_1+b$

$y_2^,=wx_2+b$

$y_3^,=wx_3+b$

…

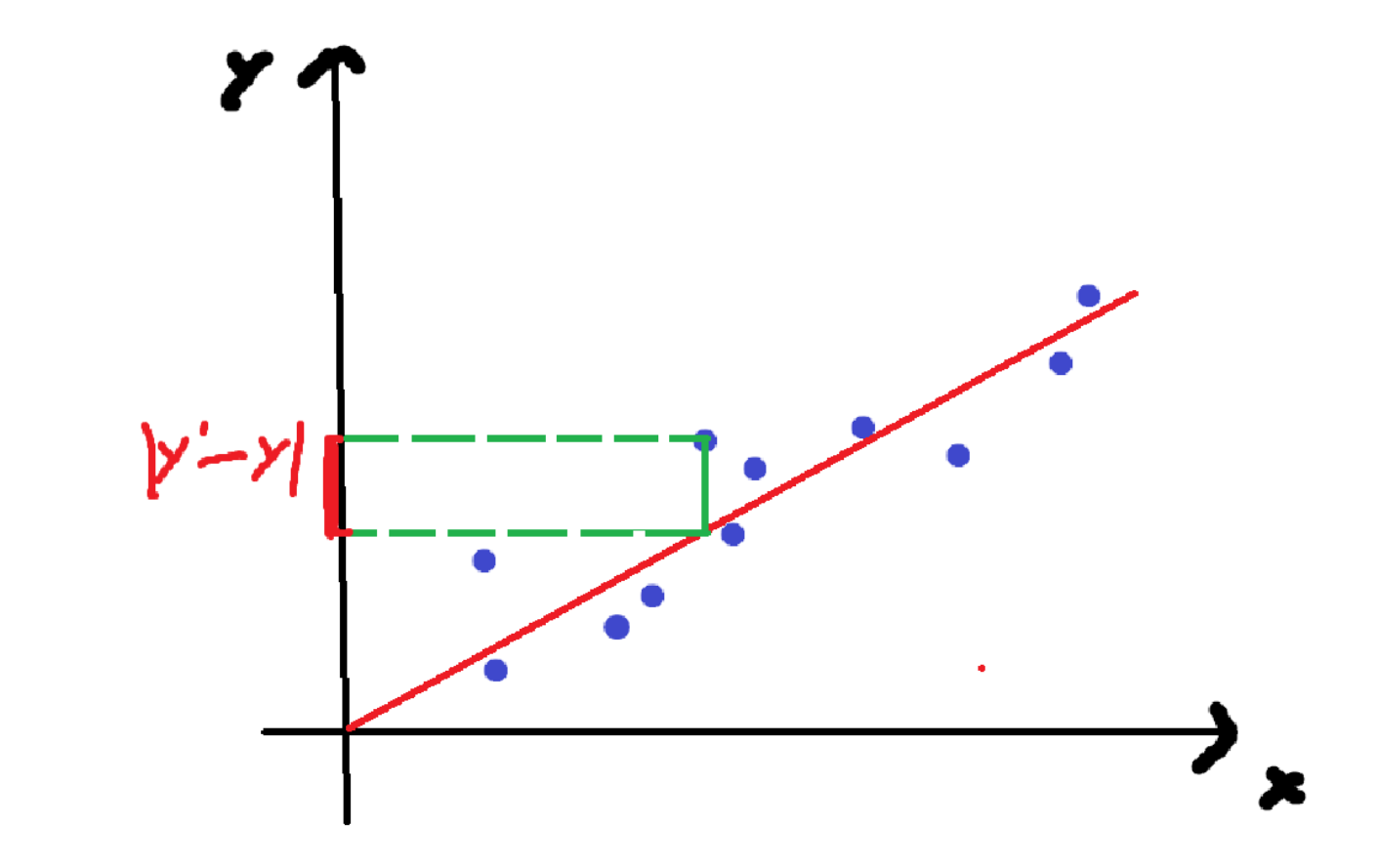
在這里插入圖片描述

將每個點的真實值與計算值的差值全部算出來

總誤差(損失):

loss= ${(y_1-y_1^,)^2}+{(y_2-y_2^,)^2}+....{(y_n-y_n^,)^2}$

總誤差會受到樣本點的個數的影響，樣本點越多，該值就越大，所以我們可以對其平均化，求得平均值

這樣就得到了損失函數:

$eˉ=1n∑i=1n(yi?wxi?b)2\bar e = \frac{1}{n} \textstyle\sum_{i=1}^{n}(y_{i}-w x_{i} - b)^{2}$

線性回歸的目標是找到最優參數 w，使總損失最小化。

方法 1：解析解（最小二乘法）

通過對損失函數求導并令導數為 0，直接參數的解析解。

步驟 1：將預測值表示為矩陣形式

設特征矩陣為 X（含截距項時，首列全為 1），維度為 m X (n+1)；

參數向量為 (w = (w_0, w_1, …, w_n)^T)；

真實標簽向量為 y=(y1,…,y**m)T。則預測值向量為： y’ = Xw

步驟 2：將總損失函數表示為矩陣形式

$loss=12∣∣(XW?y)∣∣2求導:loss=\frac{1}{2}||(XW-y)||^2 求導:$

$loss=12(XW?y)T(XW?y)loss=\frac{1}{2}(XW-y)^T(XW-y)$

$loss=12(WTXT?yT)(XW?y)loss=\frac{1}{2}(W^TX^T-y^T)(XW-y)$

$loss=12(WTXTXW?WTXTy?yTXW+yTy)loss=\frac{1}{2}(W^TX^TXW-W^TX^Ty-y^TXW+y^Ty)$

步驟 3：對 w 求導并令導數為 0

$loss′=12(WTXTXW?WTXTy?yTXW+yTy)′loss'=\frac{1}{2}(W^TX^TXW-W^TX^Ty-y^TXW+y^Ty)'$

$loss′=12(XTXW+(WTXTX)T?XTy?(yTX)T)loss'=\frac{1}{2}(X^TXW+(W^TX^TX)^T-X^Ty-(y^TX)^T)$

$loss′=12(XTXW+XTXW?XTy?XTy)loss'=\frac{1}{2}(X^TXW+X^TXW-X^Ty-X^Ty)$

$loss′=12(2XTXW?2XTy)loss'=\frac{1}{2}(2X^TXW-2X^Ty)$

$loss'=X^TXW-X^Ty$

令導數 $l os s^{'} = 0$

$0=X^TXW-X^Ty$

$X^TXW=X^Ty$

矩陣沒有除法,使用逆矩陣轉化

$X^TX)^{-1}(X^TX)W=(X^TX)^{-1}X^Ty$

$W=(X^TX)^{-1}X^Ty$

方法 2：鏈式求導（梯度下降法）

當 $X^TX$ 不可逆（如特征存在多重共線性）或樣本量極大時，解析解計算復雜，需用梯度下降法迭代求解：

內部函數是 f(W) = XW - y ，外部函數是 g(u) = 1/2 *u^2 ，其中 u = f(W) 。

外部函數的導數：
$\frac{\partial g}{\partial u} = u = XW - y$
內部函數的導數：
$\frac{\partial f}{\partial W} = X^T$
應用鏈式法則，我們得到最終的梯度：
$\frac{\partial L}{\partial W} = \left( \frac{\partial g}{\partial u} \right) \left( \frac{\partial f}{\partial W} \right) = (XW - y) X^T$

sklearn.linear_model.LinearRegression()

fit_intercept：是否計算此模型的截距(偏置)b, default=True
屬性
- coef_ 回歸后的權重系數w
- intercept_ 偏置

from sklearn.linear_model import LinearRegression
import numpy as np
data=np.array([[0,14,8,0,5,-2,9,-3,399],[-4,10,6,4,-14,-2,-14,8,-144],[-1,-6,5,-12,3,-3,2,-2,30],[5,-2,3,10,5,11,4,-8,126],[-15,-15,-8,-15,7,-4,-12,2,-395],[11,-10,-2,4,3,-9,-6,7,-87],[-14,0,4,-3,5,10,13,7,422],[-3,-7,-2,-8,0,-6,-5,-9,-309]])
x = data[:,:-1]
y = data[:,-1]
# fit_intercept=True : 有w0
model = LinearRegression(fit_intercept=True)
# 訓練
model.fit(x,y)# 查看參數
print(model.coef_)
# 查看w0
print(model.intercept_)

[ 3.41704677  9.64733333  9.96900258  0.49065266 10.67072206  4.5085292217.60894156 12.27111727]
18.18163864119797

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/web/91334.shtml
繁體地址，請注明出處：http://hk.pswp.cn/web/91334.shtml
英文地址，請注明出處：http://en.pswp.cn/web/91334.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！