圖-多對多

Graph（V,E），圖（頂點Vertex，邊Edge）

圖可以沒有邊，只有一個頂點也叫圖，但是單獨的一條邊，或者一個頂點連一條邊，不能叫圖

有向圖：

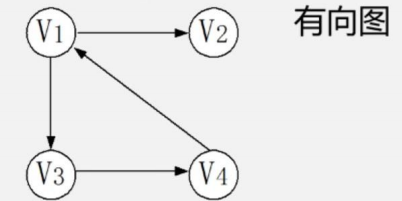
無向圖：

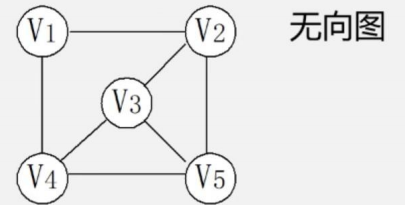
完全圖：任意兩個頂點都有一條邊相連

無向完全圖：n個頂點，n（n-1）/2條邊

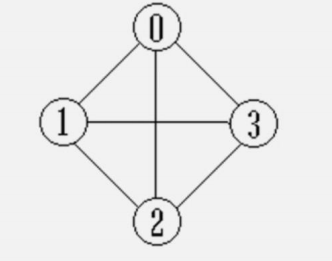
有向圖：n個頂點，n（n-1）條邊

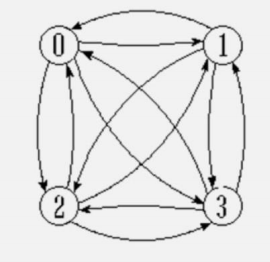
稀疏圖：有很少邊或弧的圖（e<nlogn，以2為底）
稠密圖：有較多邊或弧的圖
網：邊 / 弧帶權的圖

鄰接： 有邊 / 弧相連的兩個頂點之間的關系
存在(vi, vj)，則稱vi和vj互為鄰接點--->無向
存在<vi, vj>，則稱vi鄰接到vj，vj鄰接于vi--->有向

關聯 (依附)：邊 / 弧與頂點之間的關系
存在(vi, vj)、<vi, vj>， 則稱該邊 / 弧關聯于vi和vj

頂點的度：與該頂點相關聯的邊的數目，記為TD(v)

頂點的度：在無向圖中，頂點的度數之和等于邊數的2倍

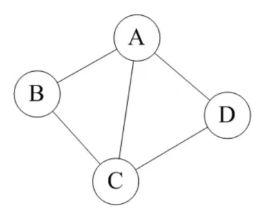
在有向圖中，所有頂點的出度之和 = 入度之和 = 弧的數量

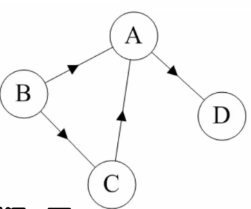
在有向圖中, 頂點的度等于該頂點的入度與出度之和

頂點v的入度是以v為終點的有向邊的條數, 記作ID(v) input

頂點v的出度是以v為始點的有向邊的條數, 記作OD(v) output

用例子分析加深理解：

下圖中V0有兩條邊，所以度為2，V1有三條邊，度為3，以此類推

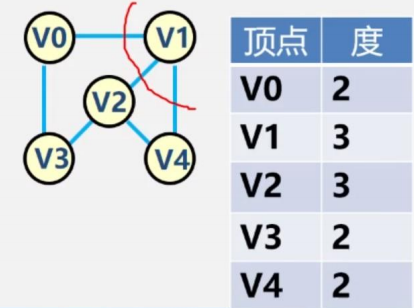
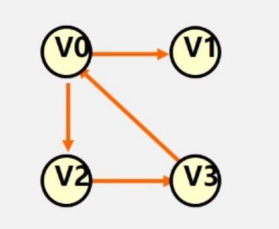
下圖中，V0出度的有兩條（V0-->V1,V0-->V2)，入度有一條（V3-->V0），所以度是2+1=3

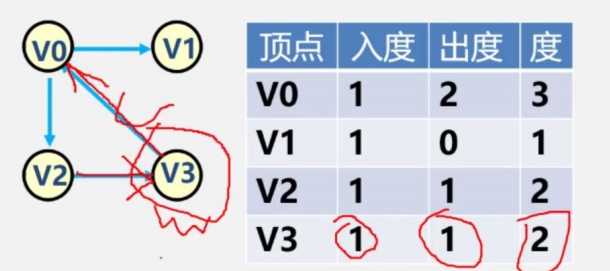
如果僅有一個頂點的入度為0，其余頂點入度均為1，是什么形狀？

答案：樹

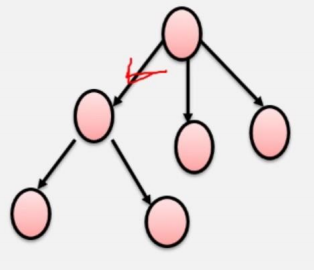
路徑：接續的邊構成的頂點序列

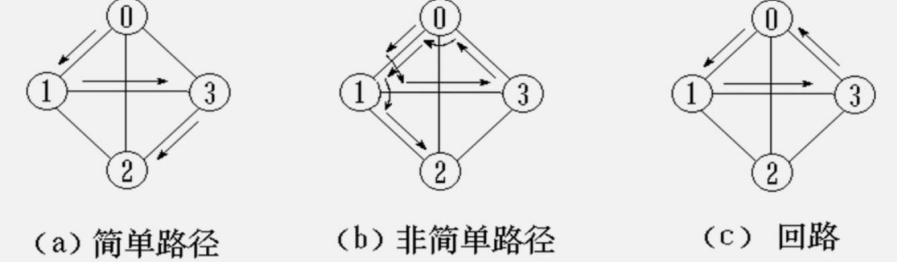
路徑長度：路徑上邊或弧的數目/權值之和

回路(環)：第一個頂點和最后一個頂點相同的路徑

簡單路徑：除路徑起點和終點可以相同外，其余頂點均不相同的路徑

簡單回路(簡單環)：除路徑起點和終點相同外，其余頂點均不相同的路徑

連通圖--無向

強連通圖--有向

連通圖是針對無向圖的，而強連通是針對有向圖的，這兩者的定義均是在圖中，任取兩個頂點u、v，均存在u到v的路徑

我們那幾張圖分析一下：

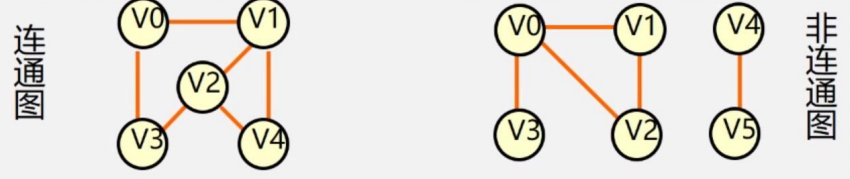
上圖中，左圖是連通圖，我們不難發現，任取兩個頂點，他們之間是有路徑可以連接的，比如V0到V2，可以是V0-->V1-->V2的路徑

右圖是非連通圖，V1是到不了V4的等等

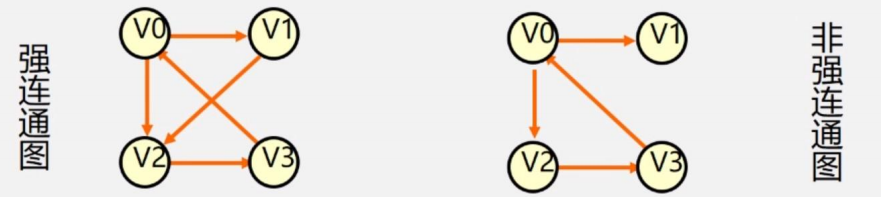
上圖中，左圖是強連通圖，任取兩個頂點，都有路徑能往返

而右圖是非強連通，我們發現，V1是到不了V0和V3的

子圖：a子圖的頂點包含于b子圖的頂點，同時a子圖的邊也包含于b子圖的邊，我們稱a是b的子圖

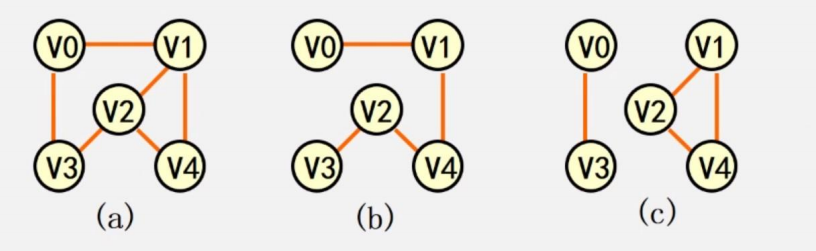
很顯然，b、c是a的子圖

有向圖G 的極大強連通子圖稱為G的強連通分量

極大強連通子圖意思是：該子圖是G的強連通子圖，將D的任何不在該子圖中的頂點加入，子圖不再是強連通的

下圖很明顯是一個非強連通圖，因為V1到不了V0，但是如果把V1單獨拿開，把V0.V2,V3構成的強連通圖也單獨拿開，就會變成圖二

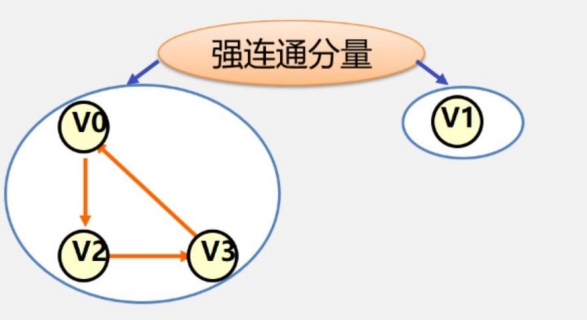
極小連通子圖：該子圖是G 的連通子圖，在該子圖中刪除任何一條邊，子圖不再連通

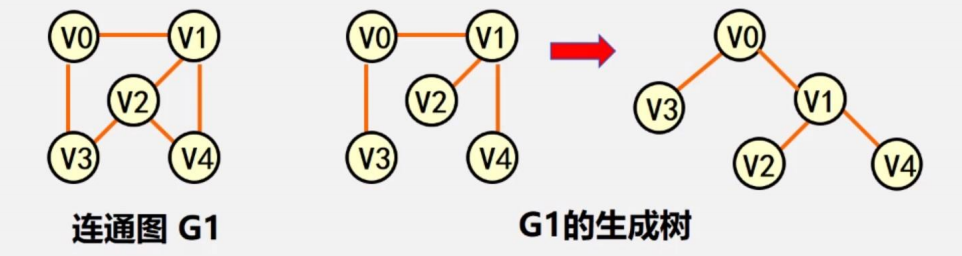
生成樹：包含無向圖G 所有頂點的極小連通子圖

在無向連通圖中，極小連通子圖實際上就是該圖的生成樹?

生成森林：對非連通圖，由各個連通分量的生成樹的集合