一、環形鏈表Ⅰ

1、題目描述

https://leetcode.cn/problems/linked-list-cycle

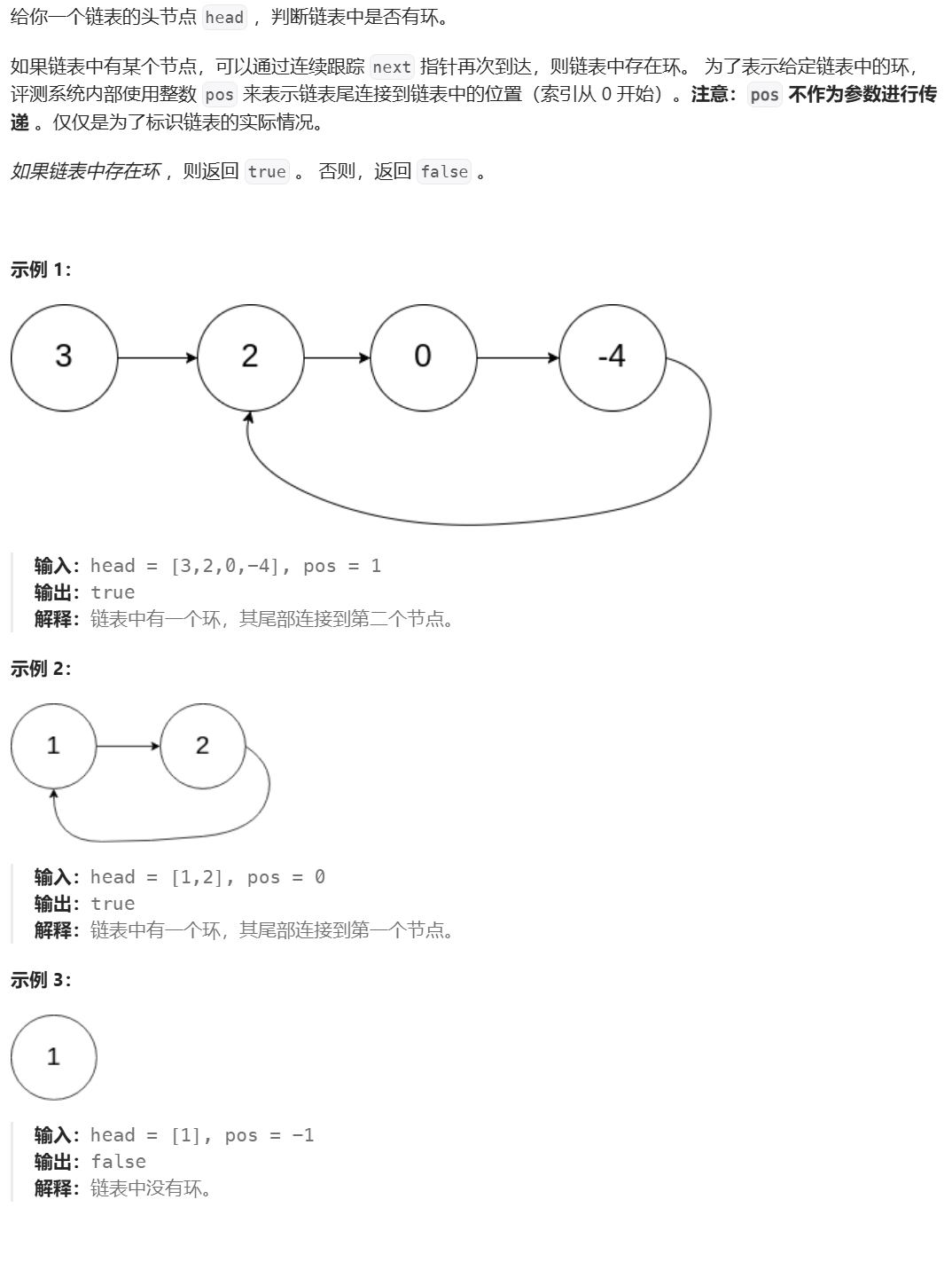
2、算法分析

思路：快慢指針?

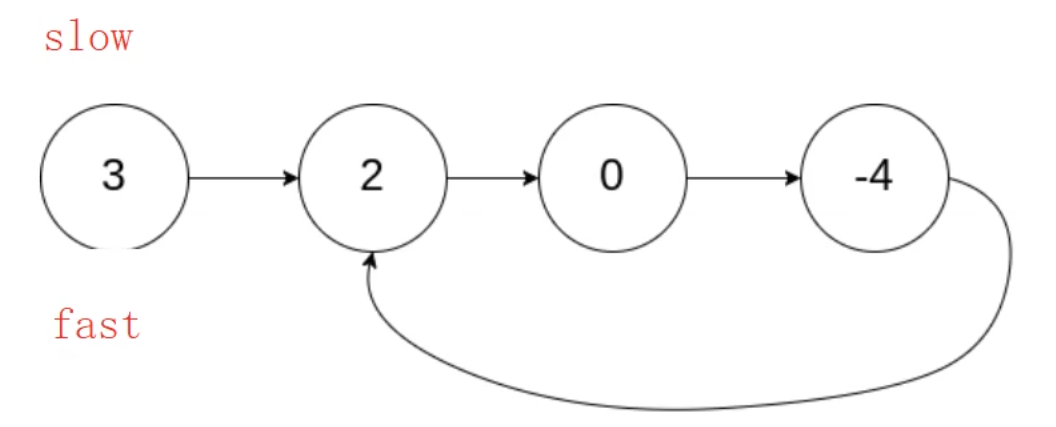
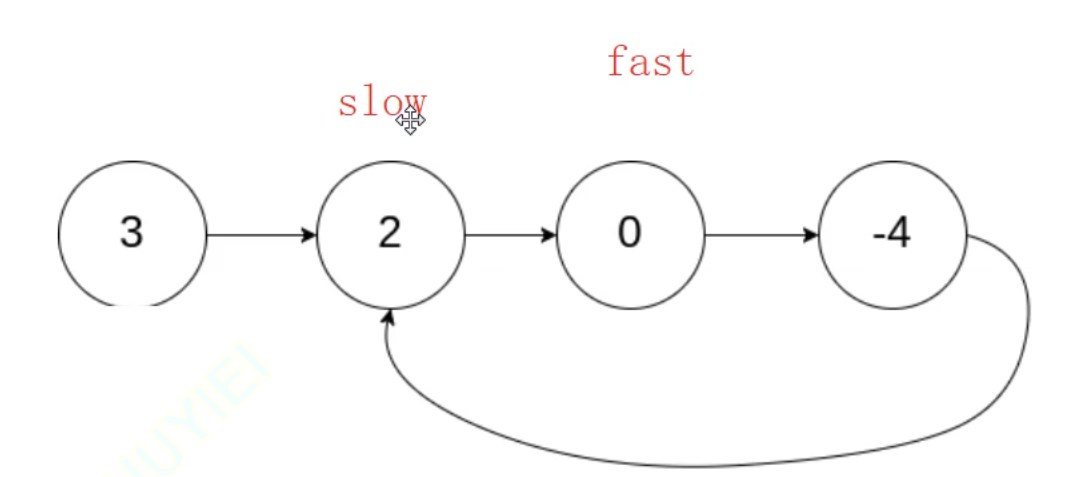
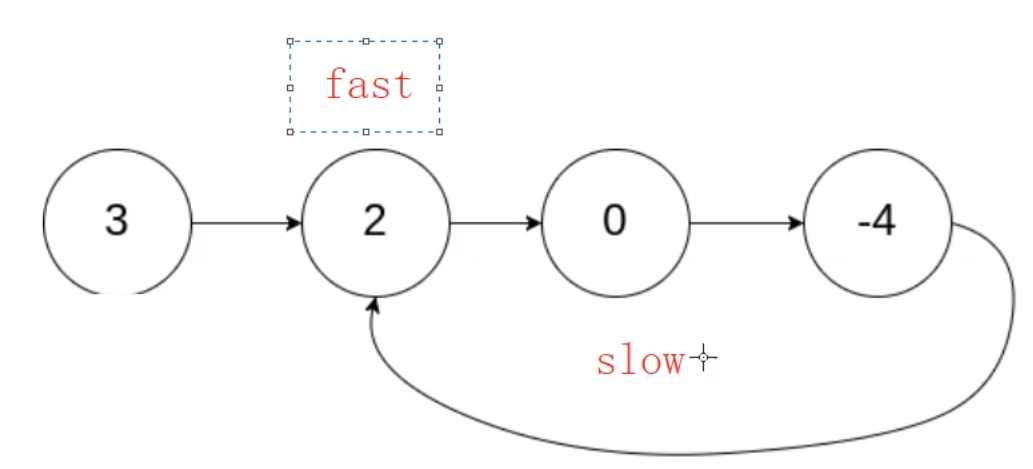
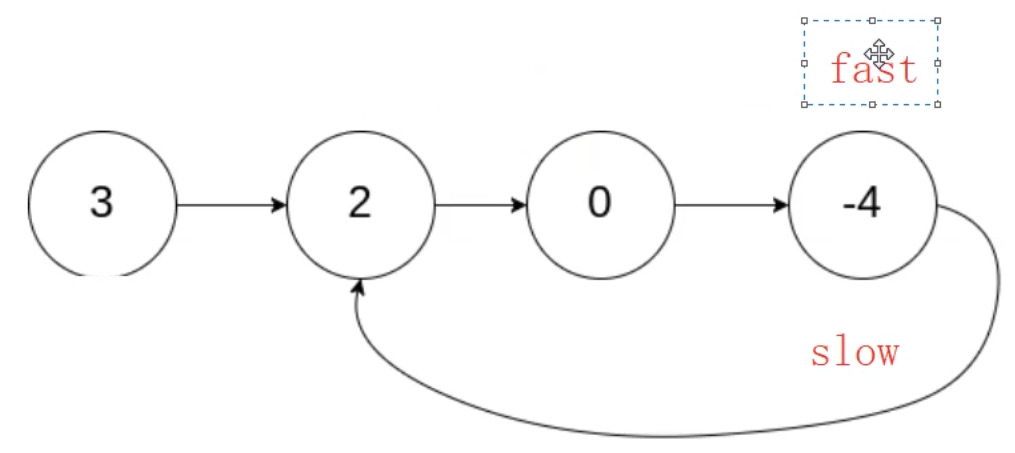
根據上圖所示的流程，我們可以推測出這樣一個結論：若鏈表帶環，快慢指針一定會相遇。

那么，這個猜測是否正確呢？下面給出嚴格的證明——

證明1：在環形鏈表中，快慢指針為什么在環里一定會相遇？（慢指針每次走一步，快指針每次走兩步）

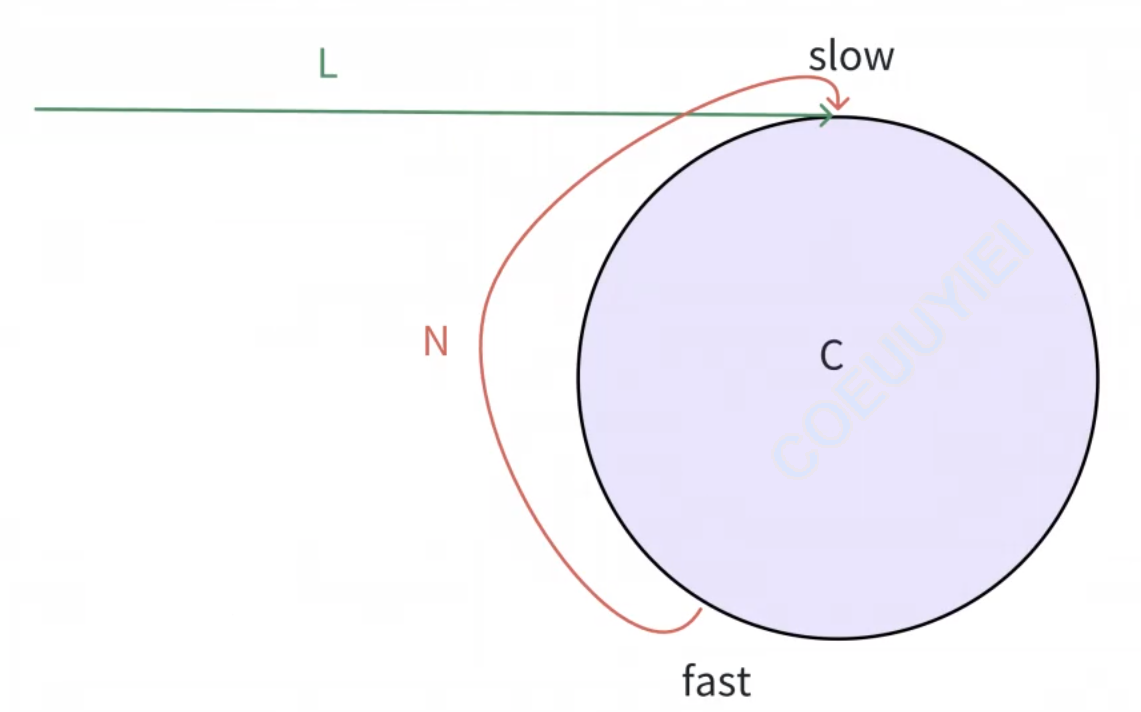
以上面的圖為例，假設slow剛入環，此時slow和fast之間的距離達到最大，最大值為N。接下來，slow前進一步，fast前進兩步，此時兩者距離變為N-1。同理，fast和slow再繼續向后走，距離依次變為N-2，N-3……2，1，0?。當距離為0時，兩指針相遇。

證明2：在環形鏈表中，慢指針每次走一步，但快指針每次走3/4/5/6……步，快慢指針在環里是否還會相遇？

假設慢指針每次走一步，快指針每次走三步。還是以剛才那副圖為例，fast和slow之間的距離依次變為N-2，N-4，……如果N為偶數，那么最后距離變為4,2,0，快慢指針相遇。但是N為奇數的話，最后距離變為3,1，-1，距離變為-1時說明出現了套圈，也就是二者并沒有相遇，此時二者之間的距離為C-1（假設環的周長為C）。那下一圈二者能否相遇呢？根據剛才的分析，當N為奇數的時候才會出現套圈的情況，若C-1為奇數，即C為偶數，一定不會相遇。若C-1為偶數，即C為奇數，下一圈一定會相遇。快指針走的總路程是慢指針的三倍，也就是3 * 慢指針 = 快指針。我們假設慢指針剛入環，快指針已經走了n圈，也就是慢指針當前走的總路程為L，快指針走的總路程為L+C-N+nC。帶入公式得：3L = L + C - N + nC。化簡得：2L = (n+1)C - N。等式左邊的2L一定是偶數，根據數學知識可以知道：①偶數 - 偶數 = 偶數? ?②奇數 - 奇數 = 偶數。所以我們得到下面的結論：C為奇數，N為奇數；C為偶數，N為偶數。但是我們先前又得到N為奇數，C為奇數一定會相遇；N為奇數，C為偶數一定不會相遇。所以C為偶數，N為奇數的情況不存在，既然不存在該情況，也就是說快指針一次走三步，最終也一定會相遇。同理，快指針每次走4、5、……步也是一樣的道理。綜上：快指針無論每次走多少步，快慢指針都可以在帶環鏈表中相遇。但是在編寫代碼時會有額外程序步驟的引入，所以我們習慣上還是快指針走兩步，慢指針走一步~

3、參考代碼

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     struct ListNode *next;* };*/
typedef struct ListNode ListNode;
bool hasCycle(struct ListNode *head) 
{//快慢指針ListNode* slow = head;ListNode* fast = head;while(fast && fast->next){slow = slow->next;fast = fast->next->next;if(slow == fast){//相遇return true;}}return false;
}

二、環形鏈表Ⅱ

1、題目描述

https://leetcode.cn/problems/linked-list-cycle-ii

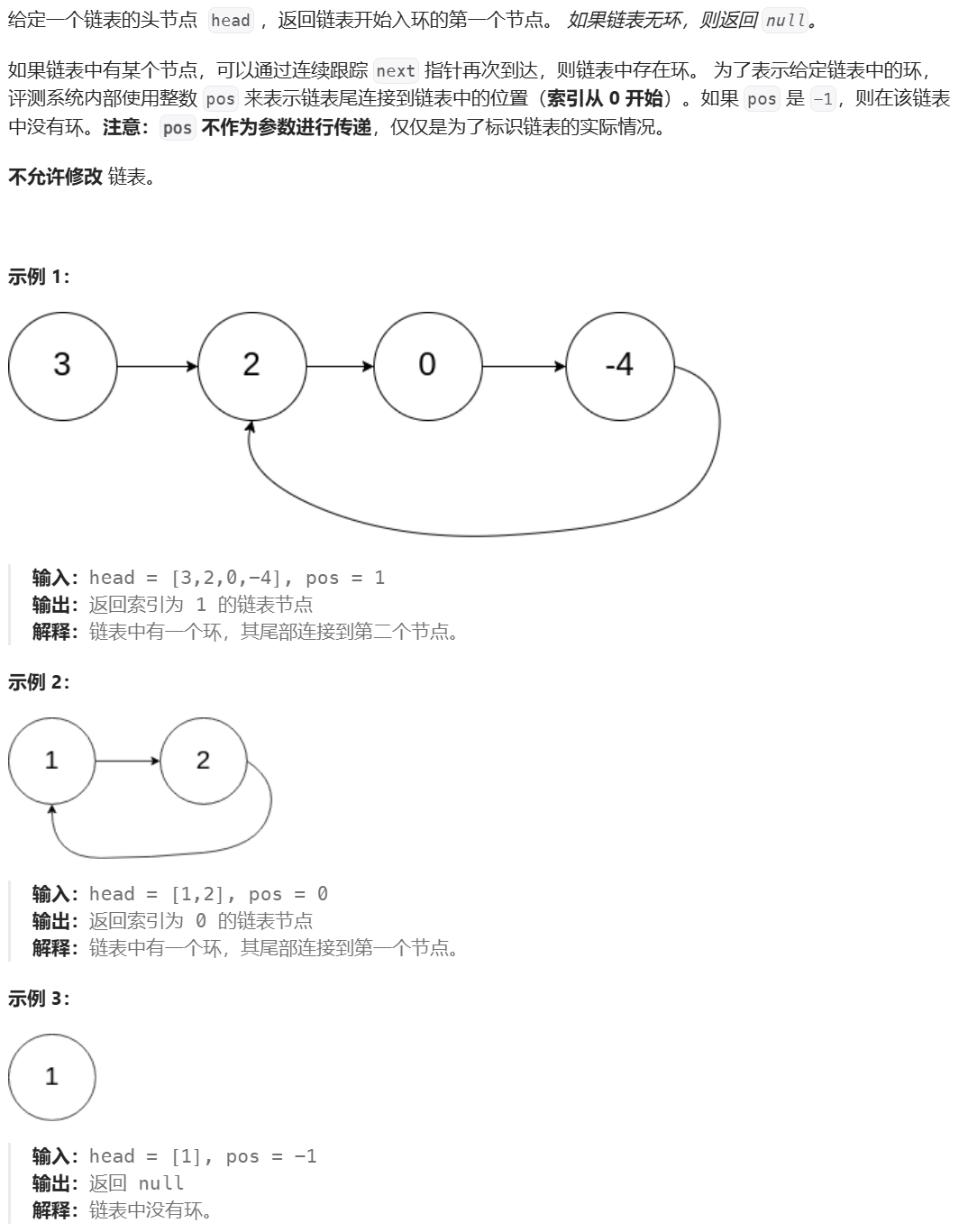
2、算法分析?

思路：快慢指針

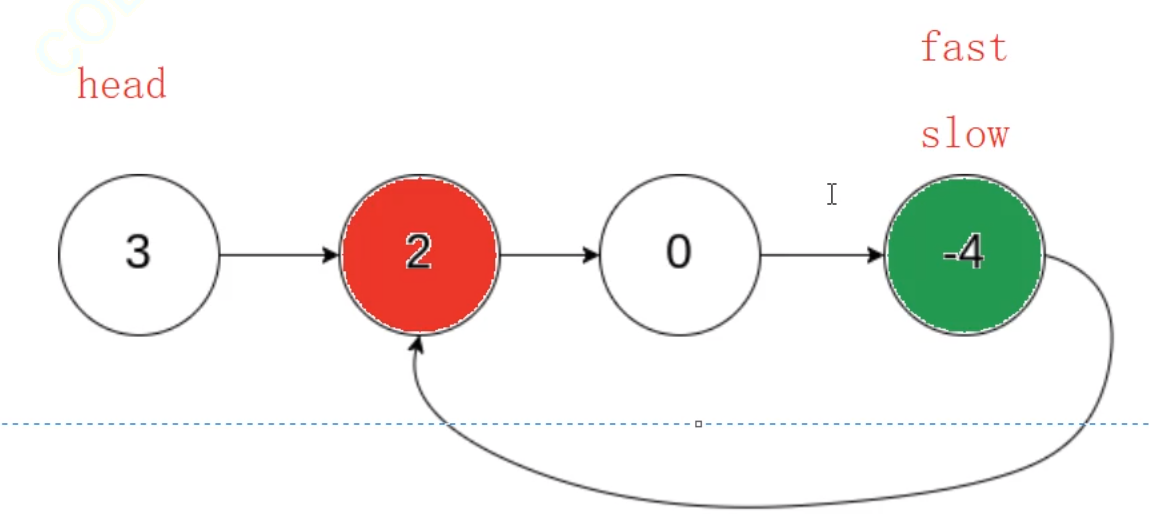
slow和fast相遇節點距離入環節點的距離為1，而頭結點距離入環節點的距離也是1~

?

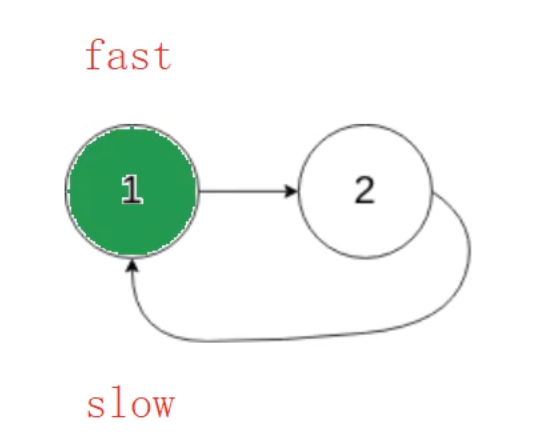?slow和fast相遇節點距離入環節點的距離為0，而頭結點距離入環節點的距離也是0~

?

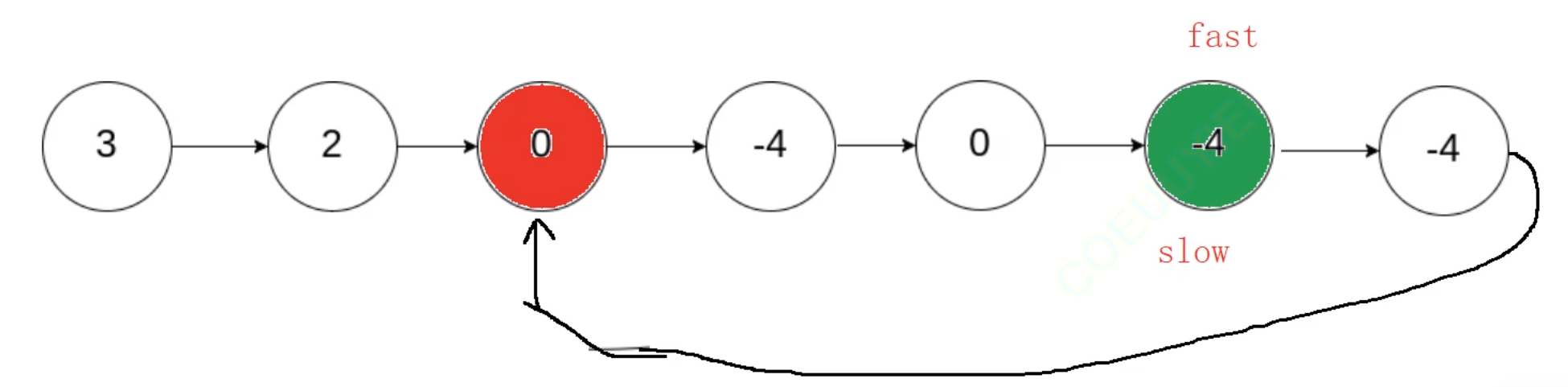?slow和fast相遇節點距離入環節點的距離為2，而頭結點距離入環節點的距離也是2~?

根據上面三個案例，我們可以作出猜想：快慢指針相遇點和頭結點到入環起始節點的距離是相等的。下面給出嚴格的證明——

證明：為什么在帶環鏈表中，快慢指針相遇點和頭結點到入環第一個結點的距離相等？

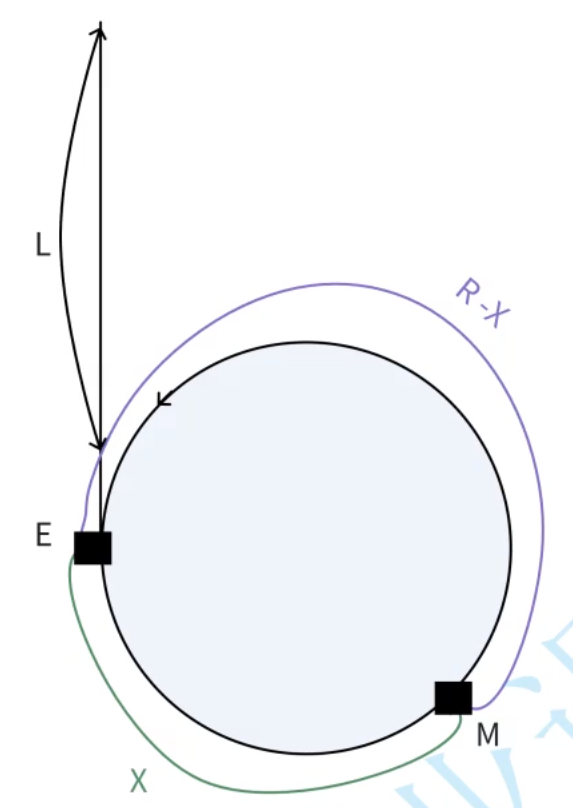
快指針走的總路程是慢指針的兩倍， 根據這句話，我們得到公式：2 * slow = fast。慢指針走過的總路程為L + X，快指針走過的總路程為L + X + nR。帶入上述公式得：2(L + X) = L + X + nR。化簡得：L + X = nR。即L = nR - X。變形一下得：L = (n-1)R + (R-X)。L是頭結點到入環第一個結點的距離，R - X是相遇點到入環第一個結點的距離，(n-1)R是走過的完整的環的路程，對師資并沒有影響，所以得到L = R - X，也就是快慢指針相遇點和頭結點到入環第一個結點的距離相等。證明完畢~

3、參考代碼

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     struct ListNode *next;* };*/
typedef struct ListNode ListNode;
struct ListNode *detectCycle(struct ListNode *head) 
{//快慢指針ListNode* slow = head;ListNode* fast = head;while(fast && fast->next){slow = slow->next;fast = fast->next->next;if(fast == slow){//找相遇點//相遇點和頭結點到入環第一個節點的距離相等ListNode* pcur = head;while(pcur != slow){slow = slow->next;pcur = pcur->next;}//pcur == slowreturn pcur;}}return NULL;
}

三、鏈表分割

1、題目描述

2、算法分析?

思路：創建兩個鏈表（小鏈表、大鏈表），遍歷原鏈表，小的結點尾插到小鏈表中，大的節點尾插到大鏈表中，最后讓大鏈表和小鏈表首尾相連。

3、參考代碼

/*
struct ListNode {int val;struct ListNode *next;ListNode(int x) : val(x), next(NULL) {}
};*/
class Partition
{
public:ListNode* partition(ListNode* pHead, int x){//創建兩個帶頭的空鏈表ListNode* lessHead, *lessTail;lessHead = lessTail = (ListNode*)malloc(sizeof(ListNode));ListNode* greaterHead, *greaterTail;greaterHead = greaterTail = (ListNode*)malloc(sizeof(ListNode));ListNode* pcur = pHead;while(pcur){if(pcur->val < x){lessTail->next = pcur;lessTail = lessTail->next;}else{greaterTail->next = pcur;greaterTail = greaterTail->next;}pcur = pcur->next;}//大鏈表尾結點的next指針置為NULL(避免死循環)greaterTail->next = NULL;//大小鏈表首尾相連lessTail->next = greaterHead->next;ListNode* ret = lessHead->next;free(lessHead);free(greaterHead);lessHead = greaterHead = NULL;return ret;}	
};