前言

? ? ? ? 本文是小編對六道國賽試題中的最后一個試題，單向后方交會的一篇學習日志。

? ? ? ? 本文的整體架構，依舊首先拿訓練數據跟大家介紹本題涉及到的數據的屬性含義，涉及到算法的原理、執行流程和終極目的。然后附上小編用C#來實現的程序，從窗體設計到各大類體。最后的總結部分，會跟大家分享小編的一些思考，然后這也是小編的廢話文學區哈哈。

? ? ? ? 小編的任務，就是20號之前完成六道賽題的第一輪摸排。過去的日子里，從六月中旬開始吧，就一點一點研究這六個題目，從RANSAC開始，到GNSS，地圖圖幅，再到GNSS基于7月最新資訊的更新，泰森，后方，為國賽搭建起的專欄中的文章從0到9，這也是一種時間的可視化吧哈哈。

? ? ? ? 小編沒有出關于點云去噪的文章，因為這個考到的概率，emmm，不多說了大家應該懂哈哈，不過可能之后我還是會捏一篇簡單的關于這道題的思路和實現方案的分享，之后再看。

---

一、數據＆原理解析

（一）數據

• 上半部分:(相機內方位元素，考到一定會給的，知道是干嘛的就行)

  • fk(mm)：相機主距，單位為毫米（mm）。
    含義：相機鏡頭中心到像平面（感光元件）的距離，是相機的核心內方位元素（就相當于一個來確定放縮系數的參數吧）。
    作用：共線方程中需用主距計算像點與攝影中心的幾何關系，直接影響像點坐標的投影精度。

  • x0、y0：像主點坐標，單位為毫米（mm）。
    含義：相機主光軸與像平面的交點坐標，理想情況下位于像平面中心（此處均為 0）。
    作用：共線方程中需用像主點坐標校正像點位置，消除鏡頭光學中心與像平面中心不重合的誤差（簡單講，就是起一個原點的作用）。

  • m：攝影比例尺分母。
    作用：用于估計攝影中心初始 Z 坐標（Zs0 = m × fk），為迭代計算提供合理初值，加速收斂。

• 下半部分（控制點）:

  • x(mm)、y(mm)：像點坐標，單位為毫米（mm）。
    含義：控制點在影像上的投影位置坐標，就是所謂像點坐標。
    作用：作為共線方程的觀測值，與物方坐標聯立求解外方位元素。

  • X(m)、Y(m)、Z(m)：物方坐標，單位為米（m）。
    含義：控制點在地面坐標系中的實際三維坐標，真值。
    作用：作為已知基準，在共線方程中拿來解算外方位元素。

• 為啥用這些？

  • 相機內方位元素（fk、x0、y0）：就是一把尺，用這個尺子，來建立起像點和物方點的關系。（就是建立起成像與真實的關系）

  • 比例尺（m）：用來估計攝影重心高度Z滴，是為算法服務的。

  • 控制點（x、y與X、Y、Z）：像點坐標（x、y）是觀測值，反映物方點在影像上的投影位置；物方坐標（X、Y、Z）是已知真值，用于約束外方位元素的解算。兩者結合形成 “觀測 - 已知” 對，通過共線方程反推相機的位置和姿態（就是外方位元素）。

（二）核心實現方案

????????單像空間后方交會的核心目標就是通過控制點求解共線方程中的外方位元素，從而建立物方坐標與像點坐標之間的數學關系，還是一個對參數的最優估計問題。（這部分用到的各種公式的詳細介紹，小編總結之后，放在與本篇綁定的PDF中了 ，大家可參考著看）

• 旋轉矩陣（a1~c3的計算）

  • What:旋轉矩陣R是三個基本矩陣的乘積：R = R_Z(κ) · R_Y(ω) · R_X(φ)
  • Why:描述像空間坐標系到物方空間坐標系的旋轉關系，是求解像點坐標的基礎。(基本矩陣見下圖，不過只需要理解這玩意兒在干嘛就OK，公式不必太深究)

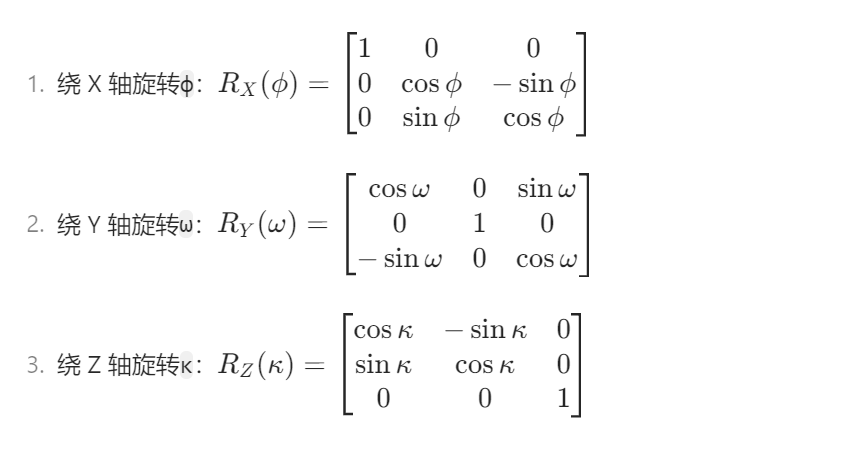
a1 = Cos(phi) * Cos(kapa) - Sin(phi) * Sin(omiga) * Sin(kapa);  // R[0,0]
a2 = -Cos(phi) * Sin(kapa) - Sin(phi) * Sin(omiga) * Cos(kapa); // R[0,1]
a3 = -Sin(phi) * Cos(omiga);                                   // R[0,2]
b1 = Cos(omiga) * Sin(kapa);                                   // R[1,0]
b2 = Cos(omiga) * Cos(kapa);                                   // R[1,1]
b3 = -Sin(omiga);                                              // R[1,2]
c1 = Sin(phi) * Cos(kapa) + Cos(phi) * Sin(omiga) * Sin(kapa);  // R[2,0]
c2 = -Sin(phi) * Sin(kapa) + Cos(phi) * Sin(omiga) * Cos(kapa); // R[2,1]
c3 = Cos(phi) * Cos(omiga);                                    // R[2,2]

• 像點近似坐標計算

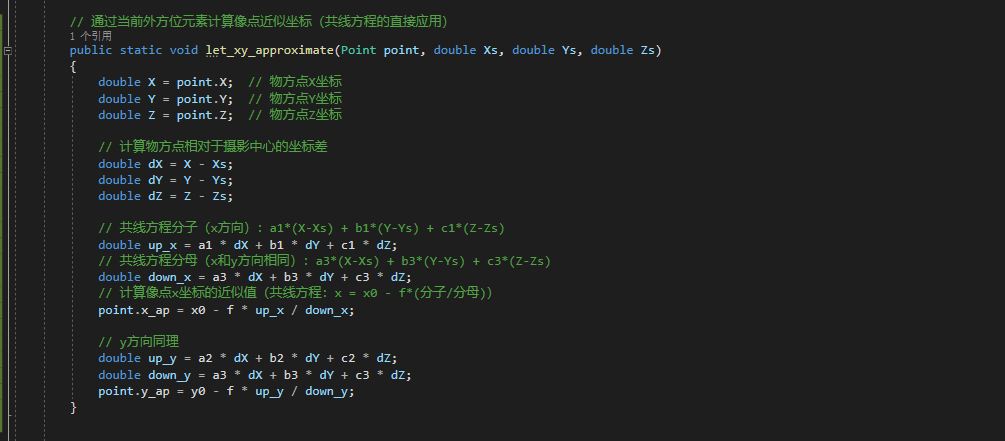
  • What:通過設置的外方位元素計算像點的近似坐標(x_ap, y_ap)，對應共線方程的直接應用。
  • Why:x_ap, y_ap是用當前外方位元素（近似值）計算的像點 “理論坐標”，后續會與觀測值(x,y)對比，計算誤差用于迭代優化。

// 計算物方點到攝影中心的偏移量
double dX = X - Xs;  // X - Xs
double dY = Y - Ys;  // Y - Ys
double dZ = Z - Zs;  // Z - Zs// 共線方程分子（x方向）：a1*(X-Xs) + b1*(Y-Ys) + c1*(Z-Zs)
double up_x = a1 * dX + b1 * dY + c1 * dZ;
// 共線方程分母（x和y方向相同）：a3*(X-Xs) + b3*(Y-Ys) + c3*(Z-Zs)
double down_x = a3 * dX + b3 * dY + c3 * dZ;
// 近似x坐標：x0 - f*(分子/分母)（對應共線方程x的表達式）
point.x_ap = x0 - f * up_x / down_x;// y方向同理
double up_y = a2 * dX + b2 * dY + c2 * dZ;
double down_y = a3 * dX + b3 * dY + c3 * dZ;
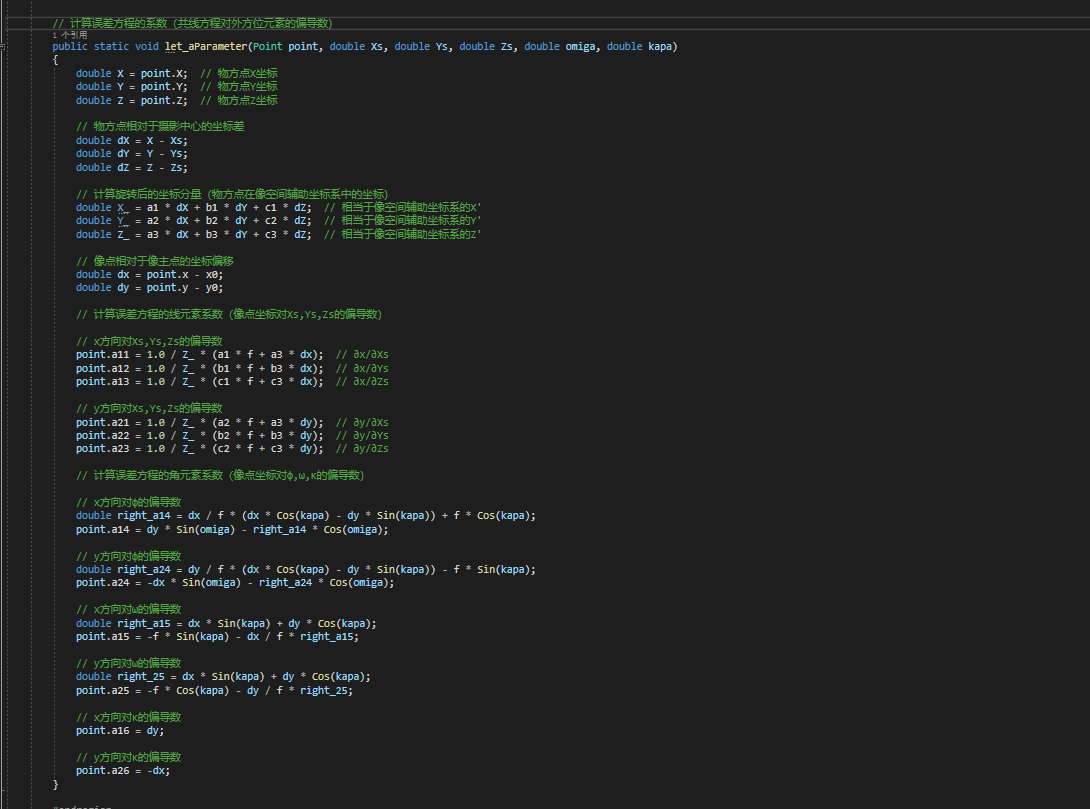
point.y_ap = y0 - f * up_y / down_y;

• 誤差方程系數

  • What:是共線方程對外方位元素的偏導數（變化率）(外方位元素有6個，每一個像點(x,y)對應 2 個偏導方程，6×2，要產生12個系數)
  • Why:把非線性的共線方程轉化為線性的誤差方程，咱們之后就是要用最小二乘來基于誤差方程進行求最優解滴。

// N = a1*dX + b1*dY + c1*dZ（共線方程分子）
double X_ = a1 * dX + b1 * dY + c1 * dZ;  
// D = a3*dX + b3*dY + c3*dZ（共線方程分母）
double Z_ = a3 * dX + b3 * dY + c3 * dZ;  
// (x - x0)：像點觀測值與像主點的偏移
double dx = point.x - x0;  
double dy = point.y - y0;  // a11 = x對Xs的偏導數：(a1*f + a3*dx)/Z_
point.a11 = 1.0 / Z_ * (a1 * f + a3 * dx);  
// a12 = x對Ys的偏導數：(b1*f + b3*dx)/Z_
point.a12 = 1.0 / Z_ * (b1 * f + b3 * dx);  
// a13 = x對Zs的偏導數：(c1*f + c3*dx)/Z_
point.a13 = 1.0 / Z_ * (c1 * f + c3 * dx);  // y方向同理（a21~a23是y對Xs,Ys,Zs的偏導數）
point.a21 = 1.0 / Z_ * (a2 * f + a3 * dy);  
point.a22 = 1.0 / Z_ * (b2 * f + b3 * dy);  
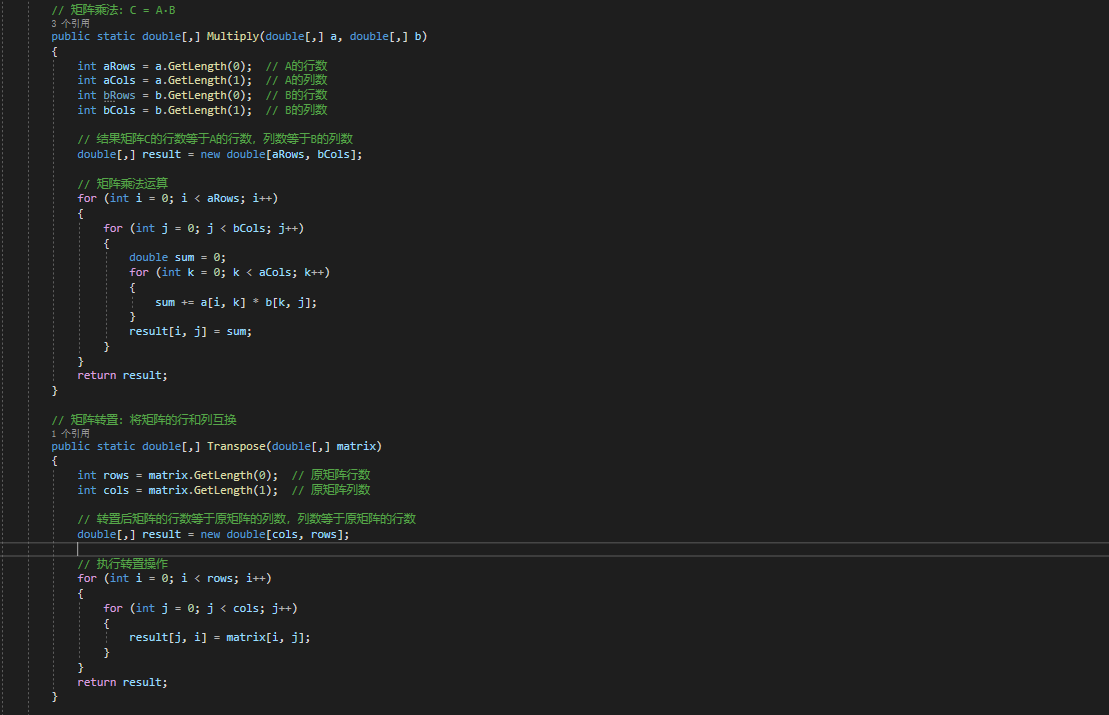
point.a23 = 1.0 / Z_ * (c2 * f + c3 * dy);  

• 最小二乘法與矩陣運算（法方程求解）

  • What:單像空間后方交會本質是 “解超定方程組”（說人話，就是方程數量多于未知數數量的方程組），咱需用最小二乘法求最優解。（又是矩陣哈哈）
  • Why:通過矩陣運算，得到外方位元素的改正數(要拿去校準現有值的尺子)，用于迭代優化。

// 1. 計算A的轉置矩陣A^T
var AT = Transpose(A);  // 2. 計算A^T·A（法方程左邊矩陣）
var ATA = Multiply(AT, A);  // 3. 計算A^T·A的逆矩陣(A^T·A)?1
var ATA_inverse = Inverse(ATA);  // 4. 計算A^T·L（法方程右邊向量）
var ATL = Multiply(AT, L);  // 5. 求解改正數ΔX = (A^T·A)?1 · (A^T·L)
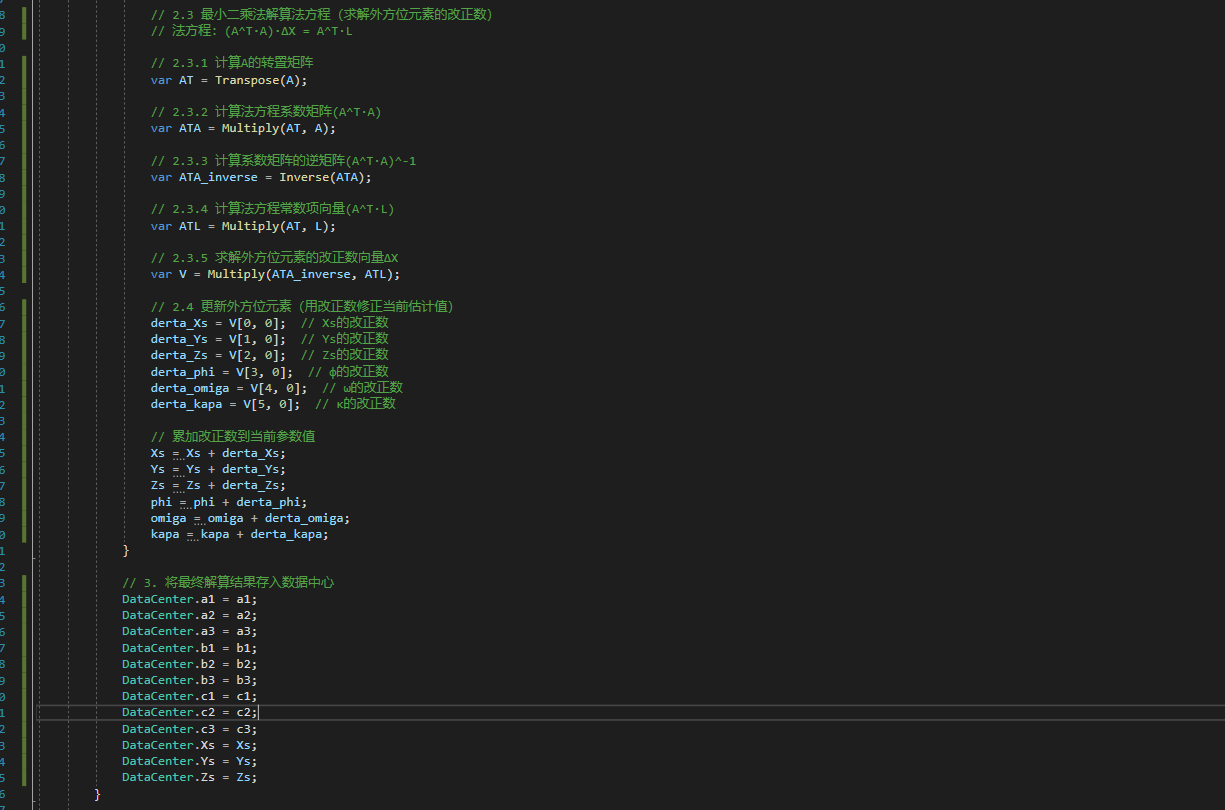
var V = Multiply(ATA_inverse, ATL);  

• 迭代更新（外方位元素的優化）

  • What:每次迭代后用改正數更新外方位元素，直到改正數足夠小,就是無限接近真值（也就是所謂收斂）。

// 用改正數更新外方位元素
derta_Xs = V[0, 0];  // ΔXs
derta_Ys = V[1, 0];  // ΔYs
// ... 其他改正數
Xs = Xs + derta_Xs;  // Xs_new = Xs_old + ΔXs
Ys = Ys + derta_Ys;  // Ys_new = Ys_old + ΔYs
// ... 其他元素同理

（三）小總結

?//這道題的整體實現思路：

• ?基操：
  • 窗體
  • 數據結構
  • 數據讀取＆管理
• 算法：
  • 一般來講，把各個步驟放到各個方法中具體實現，然后定義一個main方法作為處理入口，在這一方法中對整體算法進行調用，這樣會好看一點。以下是處理步驟：
    • 用旋轉矩陣描述相機姿態；
    • 用共線方程計算像點近似坐標；
    • 用偏導數構建誤差方程的系數矩陣；
    • 用法方程求解外方位元素的改正數；
    • 迭代更新外方位元素，直到收斂。? ? ? ? ? ?

---

二、C#實現

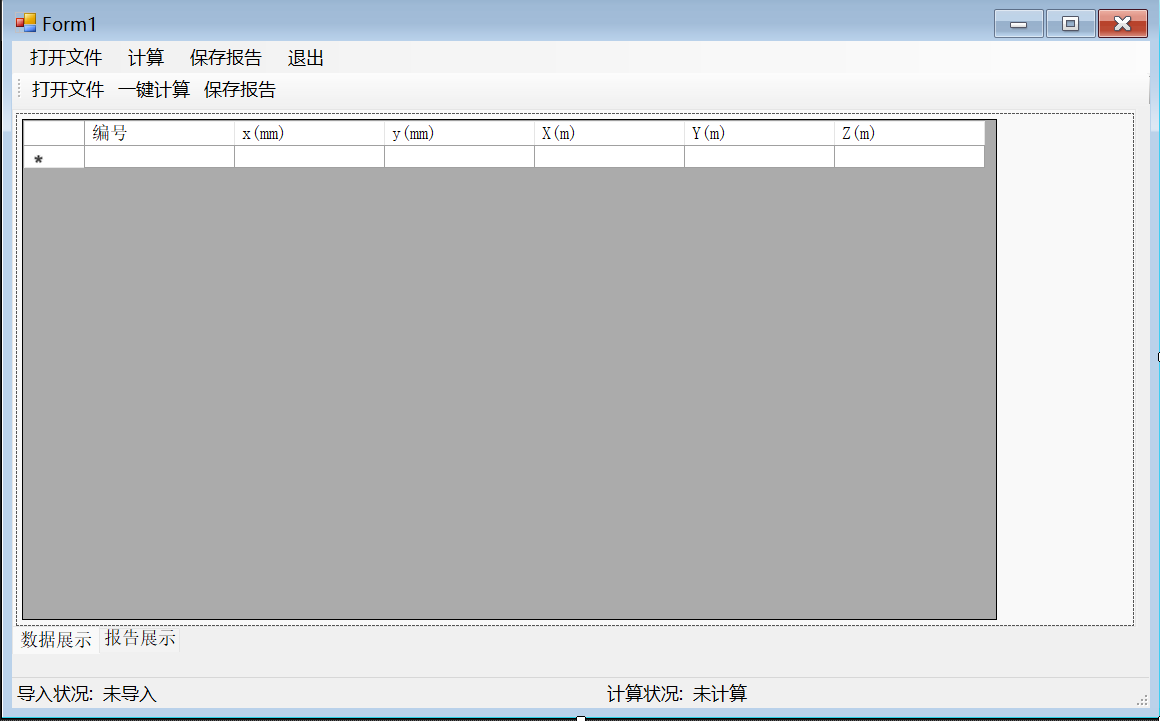
（一）窗體

//一以貫之的風格，說到做到的小編哈哈哈哈。

（二）核心算法類

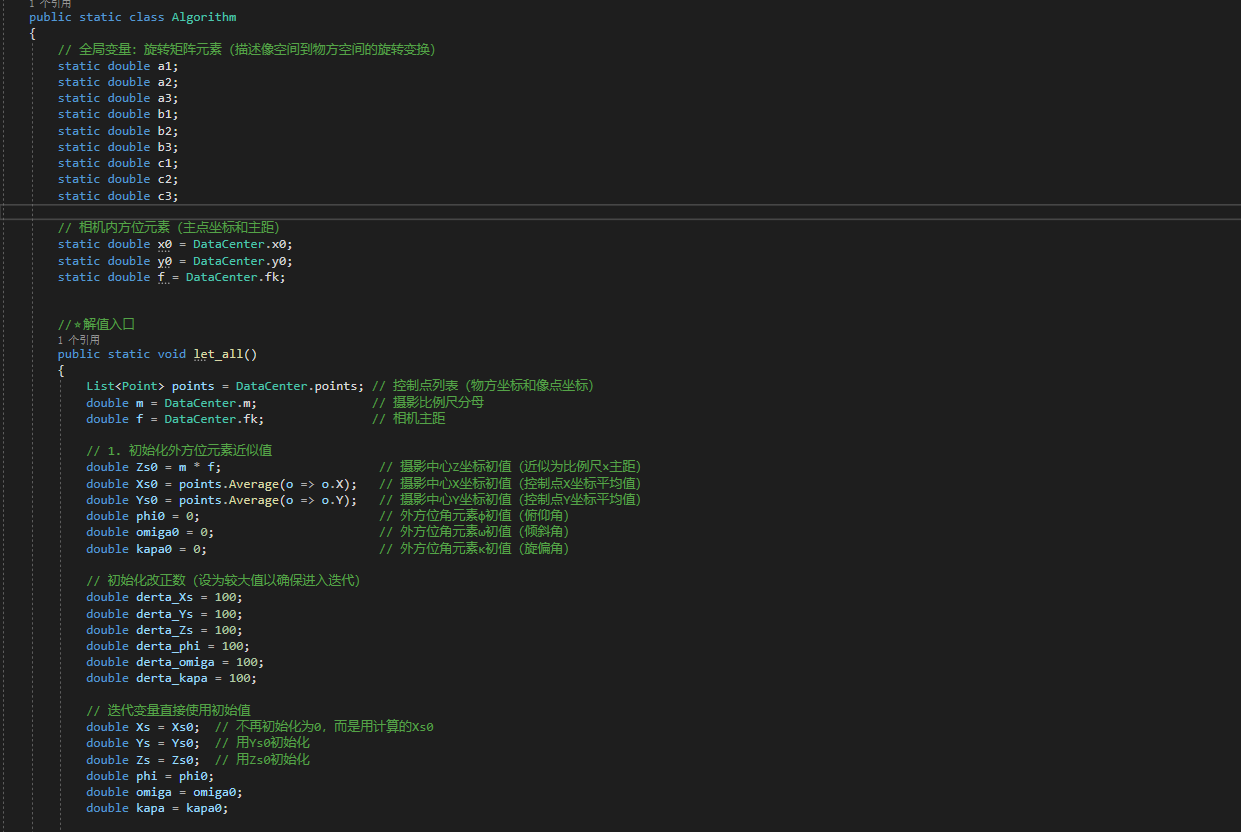
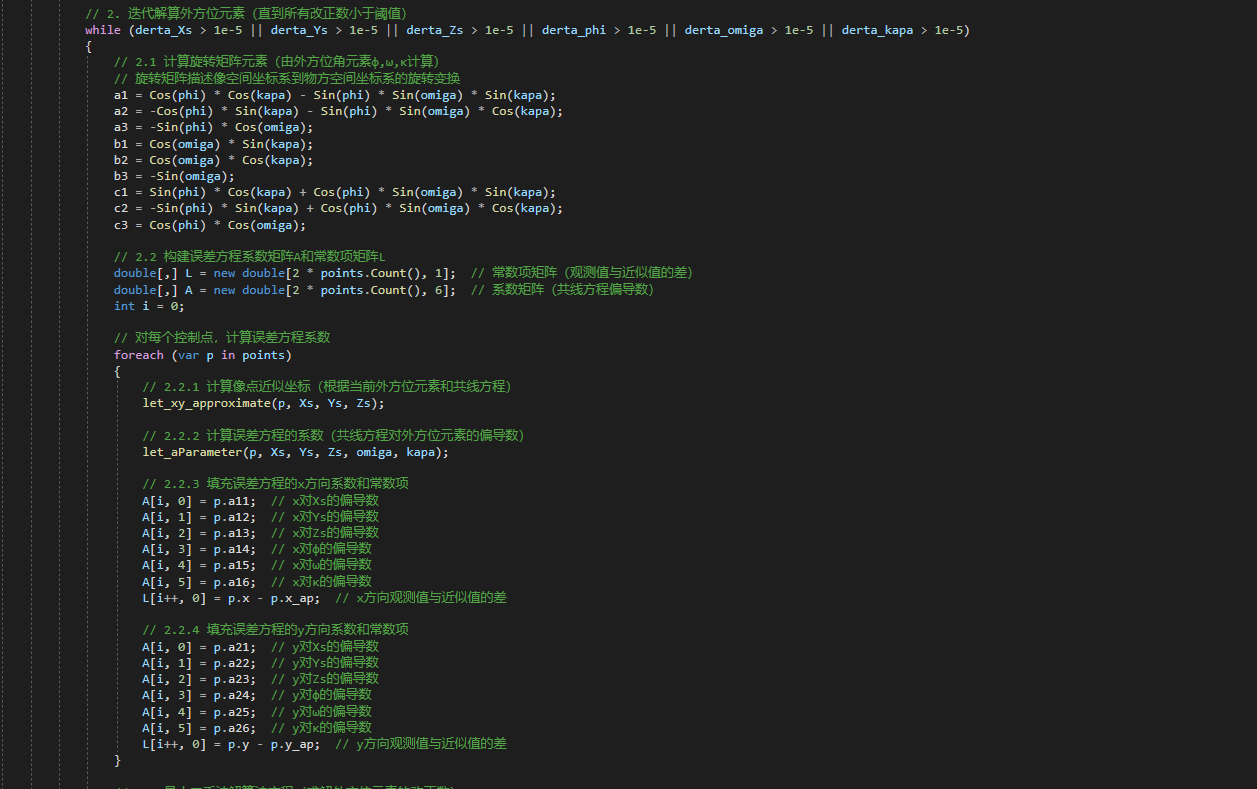
• Main

• 參數輔助

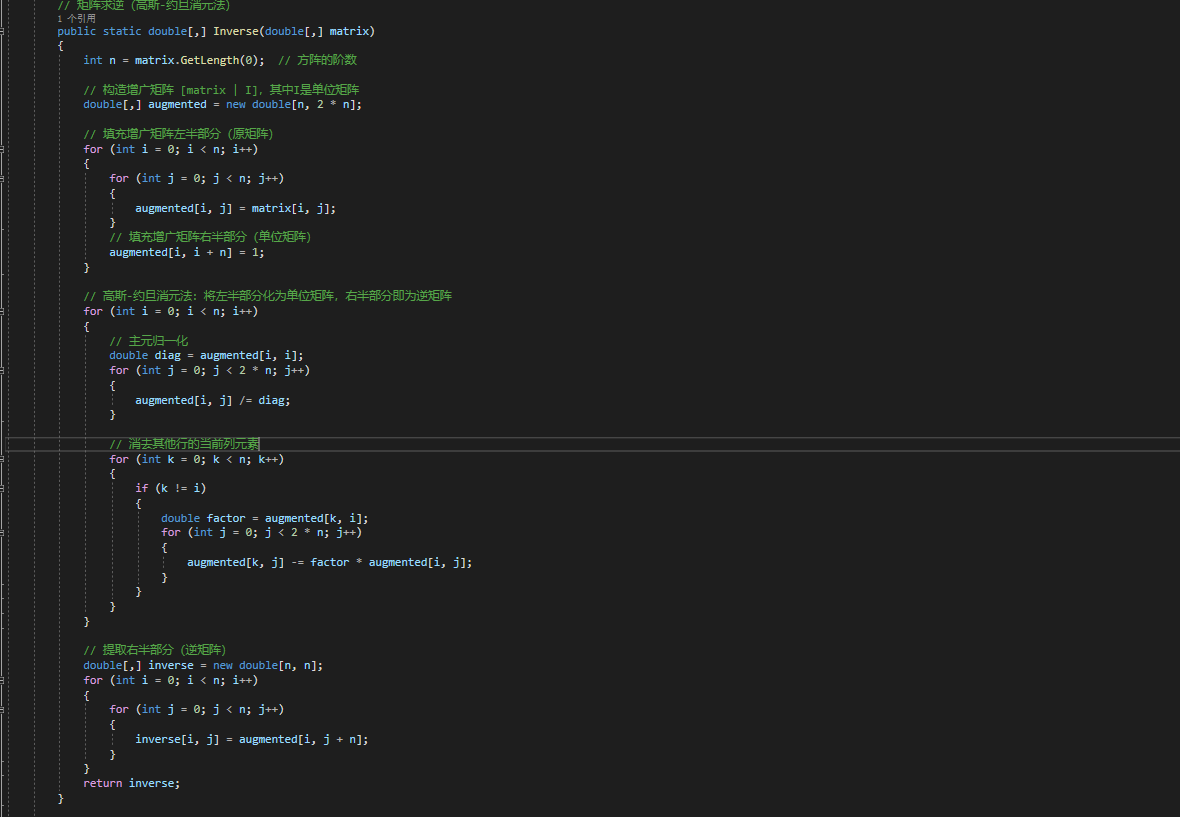
• 矩陣

（三）各大輔助類

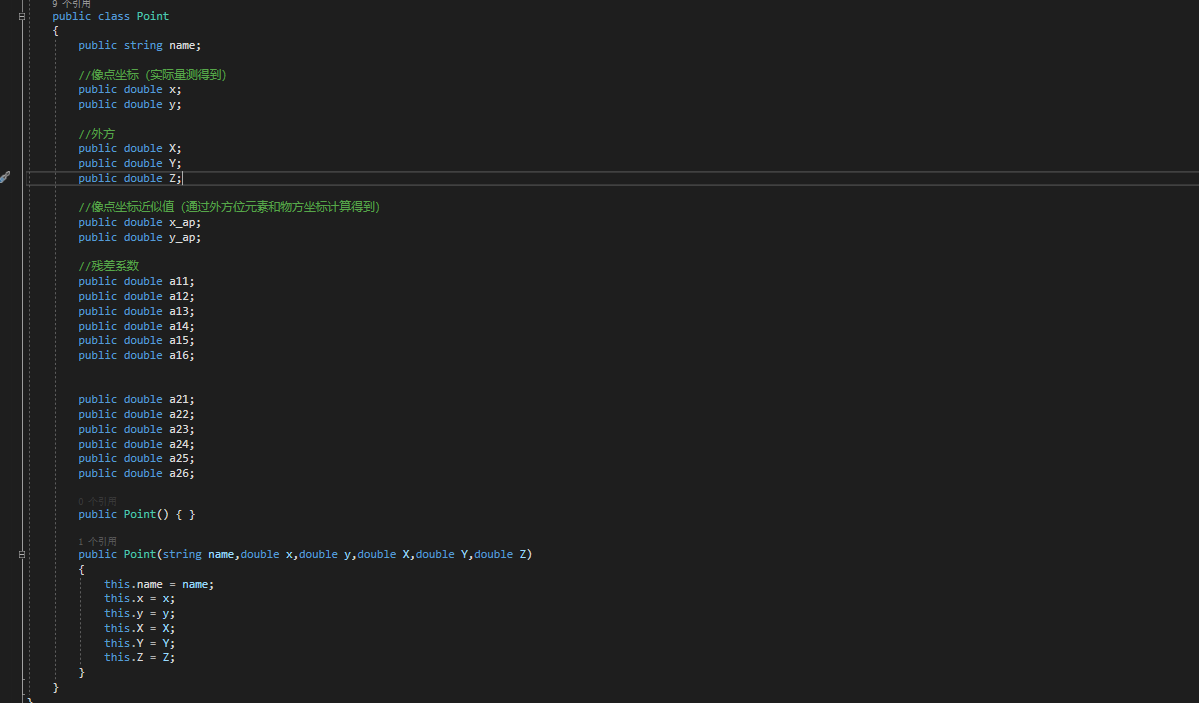
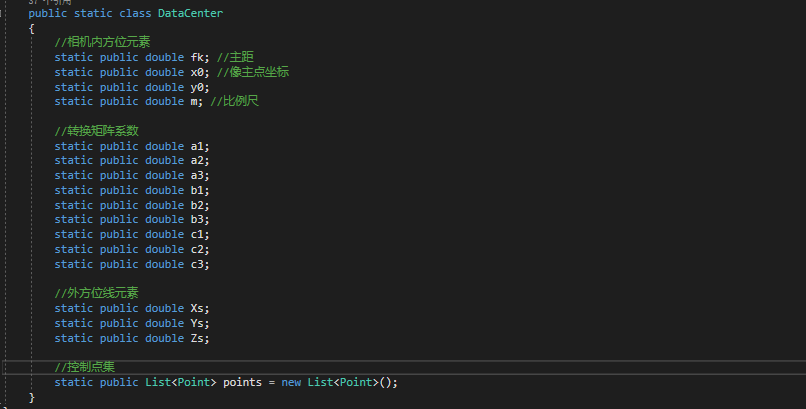
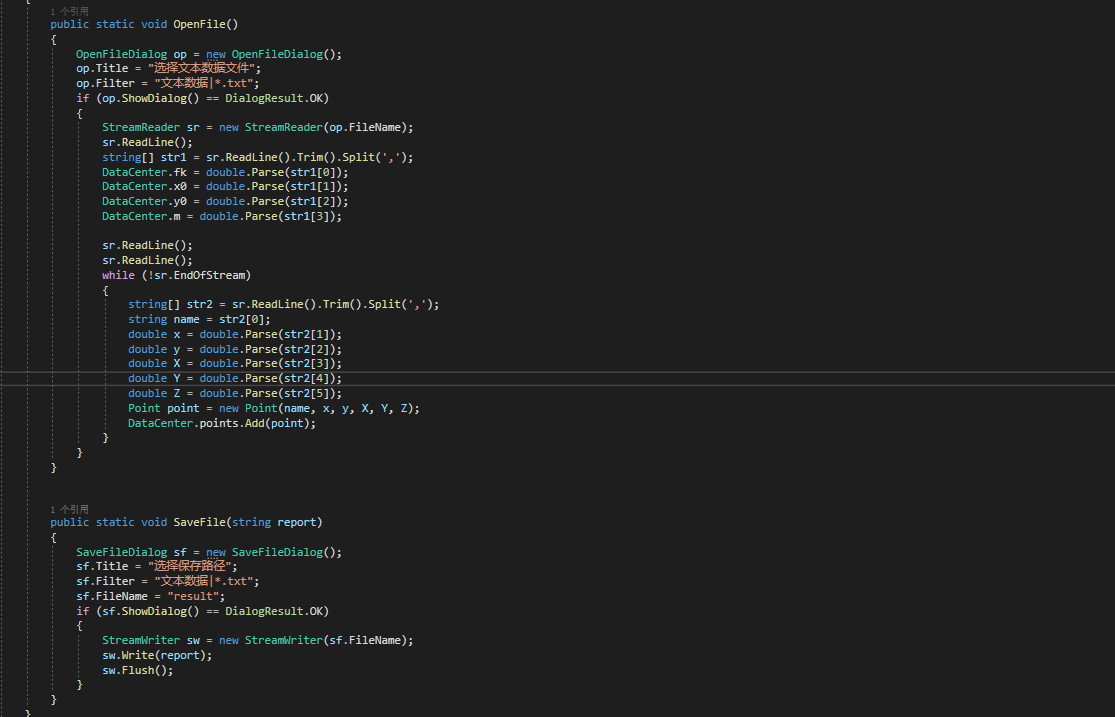
（四）結果

---

三、嘮嘮叨叨

? ? ? ? 先來總結。這道題在干的，就是用已知求參來推未知，和深度學習什么的在擬合和反演上的用意是大差不差的，都是我們拿有限的數據，來推測和繁衍出我們沒有的信息。（只不過這個有明確已知的限制參數）。

????????依舊是首先根據數據來設計數據結構類體，這里小編一個很大的感受就是在程序設計里，定義一個好的數據結構，明白數據是怎么在你的程序里流動的，真的很重要。然后設計算法，這里小編用的就是攝影測量中的常規方法，不過矩陣是真的（省略一萬字）。

? ? ? ? 這道題，考的可能性也不是多大。矩陣相關的方法撐起了核心算法的大半邊天，如果真要考，那就可以說是負和博弈了哈哈。

//以下就是小編的嘮嗑兒(廢話)區

? ? ? ? 哈哈，現在回看，沒想到已經走了這么遠了。七月過去的這兩周對小編來說可以說是一個多事之秋哈哈，無論是搬遷還是其它一些瑣事真的有時候讓小編感覺身心俱疲，但是這個過程中，小編收獲到的鼓勵支持，感受到的幸運，也真的超級多。

? ? ? ? 可能人就是需要在一些艱難困苦的日子里，才能捕獲到那些被忽視的藏在細節里的幸運吧。很感謝我的老師們，很感謝我的前輩們，也很感謝那些比我優秀的我的同伴們。很感謝我的朋友們，也很感謝你們大家。?你們都是，在險處穩穩托舉著我的力量。當然也要給自己豎一個大拇指，堅持不放棄。

? ? ? ? 其實走到了今天，于小編個人而言的，參加這場比賽的終極目標，已近乎達成了。唯結果論有其存在的意義，但站在功利之上，對個人能力的淬煉，對自我的提升，一定鋪散在日拱一卒的備賽時光和我們的雙手碰觸鍵盤時，按鍵的每一次震顫中。未來十多天，小編要做的就是在已經理解原理的基礎上，繼續深入，和賽題建立更深層的聯結，相信大家也應該都已經或早或晚進入了這個階段。未來呢，小編有什么新的感悟也會繼續把它們做成文章分享給大家，大家有想法也都可以私信或在評論區說說，評論區就是我們的聊天區哈哈。

? ? ? ? 最后還是想說，小編本人就是半瓶子晃蕩（河北話，就是“也啥也不啥”哈哈），在行文邏輯、算法理解、代碼實現上一定會存在著大大小小的問題，各位家人們如果覺得哪一部分可以再詳細或簡略一些呀，如果覺得哪里小編說的稀里糊涂或者存在錯誤呀···都可以在我們的聊天區分享出來，小編及時改正，及時調整。

????????作為一個編者，小編給自己的戒訓首先就是尊重知識，虛心受教，力爭優質。

????????一起加油。