本文是《A-VAX: Applying Quality by Design to Vaccines》第七個研究的R語言解決方案。

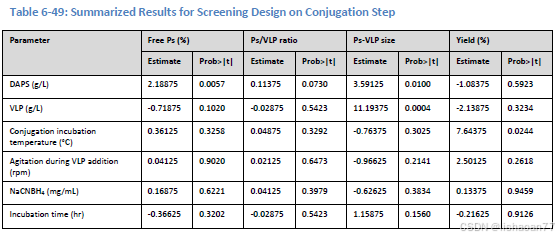
使用帶兩個中心點的二水平析因設計。運行10次實驗。結果是分辨度為III的設計。

A <- c(25,25,15,15,15,25,25,20,15,20)

B <- c(12,8,8,12,8,12,8,10,12,10)

C <- c(35,15,15,15,35,15,35,25,35,25)

D <- c(250,250,250,150,150,150,150,200,250,200)

E <- c(20,20,10,20,20,10,10,15,10,15)

F <- c(24,12,24,12,24,24,12,18,12,18)

A <- c(1,1,-1,-1,-1,1,1,0,-1,0)

B <- c(1,-1,-1,1,-1,1,-1,0,1,0)

C <- c(1,-1,-1,-1,1,-1,1,0,1,0)

D <- c(1,1,1,-1,-1,-1,-1,0,1,0)

E <- c(1,1,-1,1,1,-1,-1,0,-1,0)

F <- c(1,-1,1,-1,1,1,-1,0,-1,0)

y1<-c(11.58,12.78,7.58,7.13,8.31,10.19,13.33,9.4,7.35,11.24)

y2<-c(0.59,0.49,0.24,0.28,0.26,0.25,0.58,0.49,0.22,0.40)

y3<-c(54.36,31.31,27.57,48.32,26.85,59.2,32.84,41.21,46.24,37.73)

y4<-c(53,45,44,35,57,35,53,47,58,56)

study6<- data.frame (A=A,B=B,C=C,D=D,E=E,F=F)

#aliases( lm( y1~ (.)^4, data = study6))

mod1 <- lm( y1 ~ (.), data = study6)

summary(mod1)

> summary(mod1)

Call:

lm.default(formula = y1 ~ (.), data = study6)

Residuals:

????? 1?????? 2?????? 3?????? 4?????? 5?????? 6?????? 7?????? 8?????? 9????? 10

?0.0160 -0.2315? 0.0160? 0.0160 -0.2315 -0.2315? 0.0160 -0.4890 -0.2315? 1.3510

Coefficients:

??????????? Estimate Std. Error t value Pr(>|t|)???

(Intercept)? 9.88900??? 0.27566? 35.873 4.76e-05 ***

A??????????? 2.18875??? 0.30820?? 7.102? 0.00574 **

B?????????? -0.71875??? 0.30820? -2.332? 0.10195???

C??????????? 0.36125??? 0.30820?? 1.172? 0.32576???

D??????????? 0.04125??? 0.30820?? 0.134? 0.90200???

E??????????? 0.16875??? 0.30820?? 0.548? 0.62212???

F?????????? -0.36625??? 0.30820? -1.188? 0.32020???

---

Signif. codes:? 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.8717 on 3 degrees of freedom

Multiple R-squared:? 0.9516,??? Adjusted R-squared:? 0.8548

F-statistic: 9.829 on 6 and 3 DF,? p-value: 0.04393

mod2 <- lm( y2 ~ (.), data = study6)

summary(mod2)

> summary(mod2)

Call:

lm.default(formula = y2 ~ (.), data = study6)

Residuals:

????? 1?????? 2?????? 3?????? 4?????? 5?????? 6?????? 7?????? 8?????? 9????? 10

?0.0425 -0.0750? 0.0425? 0.0425 -0.0750 -0.0750? 0.0425? 0.1100 -0.0750? 0.0200

Coefficients:

??????????? Estimate Std. Error t value Pr(>|t|)??

(Intercept)? 0.38000??? 0.03752? 10.129? 0.00205 **

A??????????? 0.11375??? 0.04194?? 2.712? 0.07305 .

B?????????? -0.02875??? 0.04194? -0.685? 0.54229??

C??????????? 0.04875??? 0.04194?? 1.162? 0.32920??

D??????????? 0.02125??? 0.04194?? 0.507? 0.64731??

E??????????? 0.04125??? 0.04194?? 0.983? 0.39791??

F?????????? -0.02875??? 0.04194? -0.685? 0.54229??

---

Signif. codes:? 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.1186 on 3 degrees of freedom

Multiple R-squared:? 0.7837,??? Adjusted R-squared:? 0.3511

F-statistic: 1.811 on 6 and 3 DF,? p-value: 0.3347

mod3 <- lm( y3 ~ (.), data = study6)

summary(mod3)

> summary(mod3)

Call:

lm.default(formula = y3 ~ (.), data = study6)

Residuals:

????? 1?????? 2?????? 3?????? 4?????? 5?????? 6?????? 7?????? 8?????? 9????? 10

?0.2095? 0.3370? 0.2095? 0.2095? 0.3370? 0.3370? 0.2095? 0.6470? 0.3370 -2.8330

Coefficients:

??????????? Estimate Std. Error t value Pr(>|t|)???

(Intercept)? 40.5630???? 0.5500? 73.754 5.49e-06 ***

A???????????? 3.5913???? 0.6149?? 5.840 0.010002 *?

B??????????? 11.1938???? 0.6149? 18.204 0.000362 ***

C??????????? -0.7637???? 0.6149? -1.242 0.302458???

D??????????? -0.9662???? 0.6149? -1.571 0.214127???

E??????????? -0.6262???? 0.6149? -1.018 0.383437???

F???????????? 1.1588???? 0.6149?? 1.884 0.156005???

---

Signif. codes:? 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.739 on 3 degrees of freedom

Multiple R-squared:? 0.992,???? Adjusted R-squared:? 0.9761

F-statistic: 62.35 on 6 and 3 DF,? p-value: 0.003075

mod4 <- lm( y4 ~ (.), data = study6)

summary(mod4)

> summary(mod4)

Call:

lm.default(formula = y4 ~ (.), data = study6)

Residuals:

??? 1???? 2???? 3???? 4???? 5???? 6???? 7???? 8???? 9??? 10

-2.05? 0.45 -2.05 -2.05? 0.45? 0.45 -2.05 -1.30? 0.45? 7.70

Coefficients:

????????????? Estimate Std. Error t value Pr(>|t|)???

(Intercept)? 4.830e+01? 1.619e+00? 29.840 8.27e-05 ***

A??????? ???-1.000e+00? 1.810e+00? -0.553?? 0.6191???

B?????????? -2.250e+00? 1.810e+00? -1.243?? 0.3021???

C??????????? 7.750e+00? 1.810e+00?? 4.282?? 0.0234 *?

D??????????? 2.500e+00? 1.810e+00?? 1.381?? 0.2610???

E??????????? 2.728e-15? 1.810e+00?? 0.000?? 1.0000???

F?????????? -2.500e-01? 1.810e+00? -0.138?? 0.8989???

---

Signif. codes:? 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 5.119 on 3 degrees of freedom

Multiple R-squared:? 0.8806,??? Adjusted R-squared:? 0.6417

1. statistic: 3.686 on 6 and 3 DF,? p-value: 0.1558