一,引言

計數排序是一種針對整數數據的高效排序算法。其主要流程可分為三個步驟：首先計算整數數據的數值范圍；接著按大小順序統計各數值的出現次數；最后根據統計結果輸出排序后的數據序列。

二,求最值

遍歷現有數據，獲取最大值和最小值。通過計算兩者差值確定數據區間范圍，據此確定統計次數數組的分配空間大小。舉個例子：

經過遍歷得到最小值為1，最大值為9。用最大值減去最小值再加1，可得出數據范圍為1到9，共包含9個不同數值。因此需要分配能存儲9個整型數據的空間。代碼如下：

void sort(int* arr, int n)
{int min = arr[0];int max = arr[0];for (int i = 1; i < n; i++){if (arr[i] < min){min = arr[i];}if (arr[i] > max){max = arr[i];}}int* p = (int*)calloc((max - min + 1), sizeof(int));
}

三,統計次數

遍歷原數組時，先用最小值調整每個元素，將其轉換為計數數組的索引位置。隨后在計數數組對應的索引位置進行累加操作。完成所有元素的遍歷后，即可生成最終的計數數組。舉個例子：

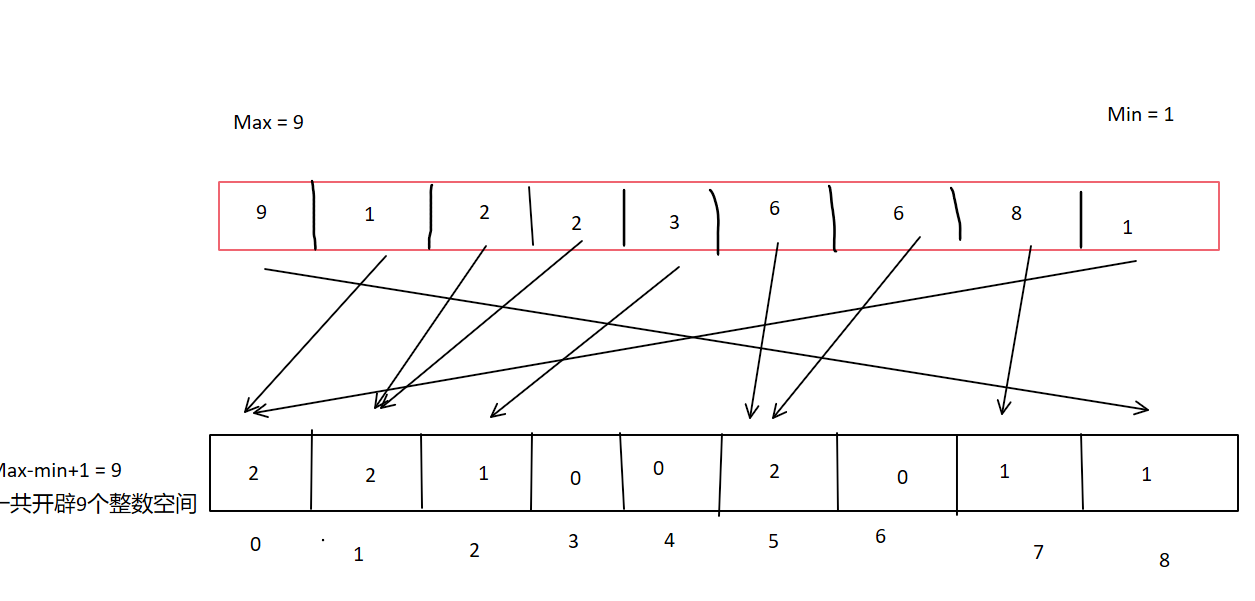
每一次箭頭的指向代表進行一次加加操作。代碼實現：
?

for (int i = 0; i < n; i++){p[a[i] - min]++;}

四,排序

統計數組的每一個數據加上min就得出原數組的值。統計數組的順序就是原數組排序后的相對位置。舉個例子：

代碼實現：

int j = 0;for (int i = 0; i < (max-min+1); i++){while (j[i]--){a[j++] = i + min;}}

五,總結

?計數排序的時間復雜度為ON遠遠小于一般排序，且該排序為穩定排序。但是計數排序要求輸入數據必須是確定范圍的整數。浮點數或字符串等數據類型無法直接使用該算法。當數據范圍k遠大于元素數量n時，需消耗O(k)額外空間存儲計數數組。若k過大（如排序少量超大整數），會造成顯著的空間浪費。對于動態范圍或未知范圍的數據，需先遍歷確定范圍值，增加預處理開銷。此過程可能影響整體效率。