DAY 48 隨機函數與廣播機制

知識點回顧：

1. 隨機張量的生成：torch.randn函數
2. 卷積和池化的計算公式（可以不掌握，會自動計算的）
3. pytorch的廣播機制：加法和乘法的廣播機制

ps：numpy運算也有類似的廣播機制，基本一致

作業：自己多借助ai舉幾個例子幫助自己理解即可

1、隨機張量的生成：torch.randn函數

# 生成3維張量（常用于圖像數據的通道、高度、寬度）
tensor_3d = torch.randn(3, 224, 224)  # 3通道，高224，寬224
print(f"3維張量形狀: {tensor_3d.shape}")  # 輸出: torch.Size([3, 224, 224])

# 生成4維張量（常用于批量圖像數據：[batch, channel, height, width]）
tensor_4d = torch.randn(2, 3, 224, 224)  # 批量大小為2，3通道，高224，寬224
print(f"4維張量形狀: {tensor_4d.shape}")  # 輸出: torch.Size([2, 3, 224, 224])

torch.rand():生成[0,1）范圍內均勻分布的隨機數

x = torch.rand(3, 2)  # 生成3x2的張量
print(f"均勻分布隨機數: {x}, 形狀: {x.shape}")

torch.randint()：生成指定范圍內的隨機整數

x = torch.randint(low=0, high=10, size=(3,))  # 生成3個0到9之間的整數
print(f"隨機整數: {x}, 形狀: {x.shape}")

torch.normal()：生成指定均值和標準差的正態分布隨機數。

mean = torch.tensor([0.0, 0.0])
std = torch.tensor([1.0, 2.0])
x = torch.normal(mean, std)  # 生成兩個正態分布隨機數
print(f"正態分布隨機數: {x}, 形狀: {x.shape}")

2、卷積和池化的計算公式（可以不掌握，會自動計算的）

3、pytorch的廣播機制：加法和乘法的廣播機制

案例 1：張量 a(3, 1)?與張量 b(3,)

• 步驟 1：補全維度
  張量的形狀可以理解為 “維度的元組”，為了對齊，先給維度少的張量補 1（在最左側補）?。這里?b?原本是?(3,)（1 維），補全后變成?(1, 3)（2 維），和?a?的維度數（2 維）對齊。
• 步驟 2：逐維擴展
  對每個維度，若其中一個張量該維度大小為?1，就復制數據擴展到另一張量的維度大小?。a?形狀是?(3, 1)，b?補全后是?(1, 3)：
  • 第 1 維（行方向）：a?是?3，b?是?1?→?b?第 1 維擴展為?3（復制自身 3 次）。
  • 第 2 維（列方向）：a?是?1，b?是?3?→?a?第 2 維擴展為?3（復制自身 3 次）。
    最終兩者都擴展為?(3, 3)，就能逐元素運算。

案例 2：張量 a(5, 1, 4)?與張量 b(1, 3, 1)

• 直接對比每個維度（從右往左）：
  • 第 3 維（最右側）：a?是?4，b?是?1?→ 兼容（1?可擴展）。
  • 第 2 維：a?是?1，b?是?3?→ 兼容（1?可擴展）。
  • 第 1 維：a?是?5，b?是?1?→ 兼容（1?可擴展）。
• 擴展后，每個維度取較大值?：第 1 維?5、第 2 維?3、第 3 維?4，最終形狀?(5, 3, 4)?，滿足廣播。

案例 3：張量 a(2, 1, 3, 4)?與張量 b(5, 1, 4)

• 步驟 1：補全維度
  b?是 3 維，a?是 4 維 → 給?b?最左側補?1，變成?(1, 5, 1, 4)?，和?a?維度數（4 維）對齊。
• 步驟 2：逐維擴展
  對比每個維度（從右往左）：
  • 第 4 維：a?是?4，b?是?4?→ 相等，無需擴展。
  • 第 3 維：a?是?3，b?是?1?→?b?第 3 維擴展為?3（復制）。
  • 第 2 維：a?是?1，b?是?5?→?a?第 2 維擴展為?5（復制）。
  • 第 1 維：a?是?2，b?是?1?→?b?第 1 維擴展為?2（復制）。
    最終形狀?(2, 5, 3, 4)?，完成廣播。

3.1加法的廣播機制

二維+一維

import torch# 創建原始張量
a = torch.tensor([[10], [20], [30]])  # 形狀: (3, 1)
b = torch.tensor([1, 2, 3])          # 形狀: (3,)result = a + b
# 廣播過程
# 1. b補全維度: (3,) → (1, 3)
# 2. a擴展列: (3, 1) → (3, 3)
# 3. b擴展行: (1, 3) → (3, 3)
# 最終形狀: (3, 3)print("原始張量a:")
print(a)print("\n原始張量b:")
print(b)print("\n廣播后a的值擴展:")
print(torch.tensor([[10, 10, 10],[20, 20, 20],[30, 30, 30]]))  # 實際內存中未復制，僅邏輯上擴展print("\n廣播后b的值擴展:")
print(torch.tensor([[1, 2, 3],[1, 2, 3],[1, 2, 3]]))  # 實際內存中未復制，僅邏輯上擴展print("\n加法結果:")
print(result)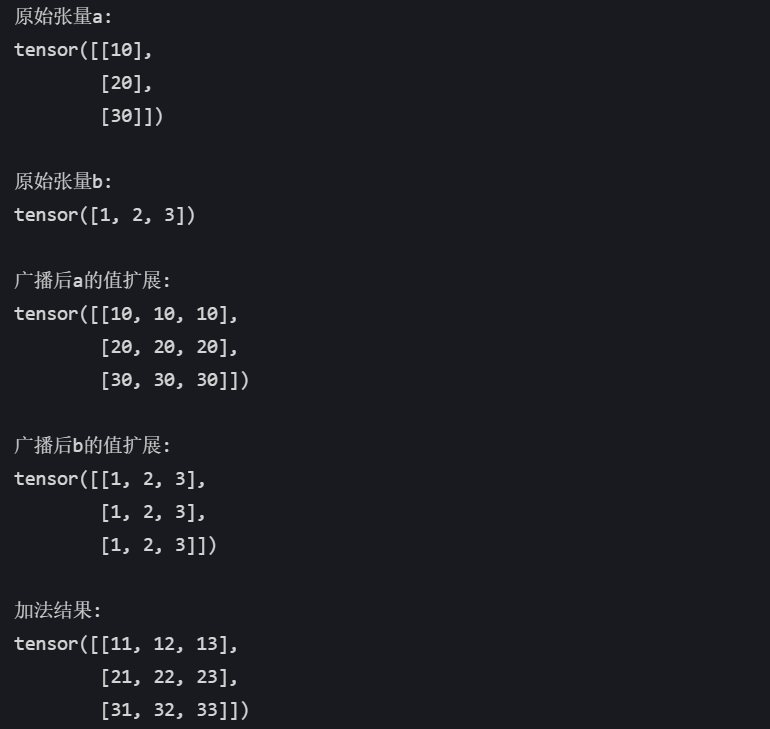

三維+二維

# 創建原始張量
a = torch.tensor([[[1], [2]], [[3], [4]]])  # 形狀: (2, 2, 1)
b = torch.tensor([[10, 20]])               # 形狀: (1, 2)# 廣播過程
# 1. b補全維度: (1, 2) → (1, 1, 2)
# 2. a擴展第三維: (2, 2, 1) → (2, 2, 2)
# 3. b擴展第一維: (1, 1, 2) → (2, 1, 2)
# 4. b擴展第二維: (2, 1, 2) → (2, 2, 2)
# 最終形狀: (2, 2, 2)result = a + b
print("原始張量a:")
print(a)print("\n原始張量b:")
print(b)print("\n廣播后a的值擴展:")
print(torch.tensor([[[1, 1],[2, 2]],[[3, 3],[4, 4]]]))  # 實際內存中未復制，僅邏輯上擴展print("\n廣播后b的值擴展:")
print(torch.tensor([[[10, 20],[10, 20]],[[10, 20],[10, 20]]]))  # 實際內存中未復制，僅邏輯上擴展print("\n加法結果:")
print(result)

二維+標量

# 創建原始張量
a = torch.tensor([[1, 2], [3, 4]])  # 形狀: (2, 2)
b = 10                              # 標量，形狀視為 ()# 廣播過程
# 1. b補全維度: () → (1, 1)
# 2. b擴展第一維: (1, 1) → (2, 1)
# 3. b擴展第二維: (2, 1) → (2, 2)
# 最終形狀: (2, 2)result = a + b
print("原始張量a:")
print(a)
# 輸出:
# tensor([[1, 2],
#         [3, 4]])print("\n標量b:")
print(b)
# 輸出: 10print("\n廣播后b的值擴展:")
print(torch.tensor([[10, 10],[10, 10]]))  # 實際內存中未復制，僅邏輯上擴展print("\n加法結果:")
print(result)
# 輸出:
# tensor([[11, 12],
#         [13, 14]])

3.2乘法的廣播機制

批量矩陣與單個矩陣相乘

import torch# A: 批量大小為2，每個是3×4的矩陣
A = torch.randn(2, 3, 4)  # 形狀: (2, 3, 4)# B: 單個4×5的矩陣
B = torch.randn(4, 5)     # 形狀: (4, 5)# 廣播過程：
# 1. B補全維度: (4, 5) → (1, 4, 5)
# 2. B擴展第一維: (1, 4, 5) → (2, 4, 5)
# 矩陣乘法: (2, 3, 4) @ (2, 4, 5) → (2, 3, 5)
result = A @ B            # 結果形狀: (2, 3, 5)print("A形狀:", A.shape)  # 輸出: torch.Size([2, 3, 4])
print("B形狀:", B.shape)  # 輸出: torch.Size([4, 5])
print("結果形狀:", result.shape)  # 輸出: torch.Size([2, 3, 5])

批量矩陣與批量矩陣相乘（部分廣播）

# A: 批量大小為3，每個是2×4的矩陣
A = torch.randn(3, 2, 4)  # 形狀: (3, 2, 4)# B: 批量大小為1，每個是4×5的矩陣
B = torch.randn(1, 4, 5)  # 形狀: (1, 4, 5)# 廣播過程：
# B擴展第一維: (1, 4, 5) → (3, 4, 5)
# 矩陣乘法: (3, 2, 4) @ (3, 4, 5) → (3, 2, 5)
result = A @ B            # 結果形狀: (3, 2, 5)print("A形狀:", A.shape)  # 輸出: torch.Size([3, 2, 4])
print("B形狀:", B.shape)  # 輸出: torch.Size([1, 4, 5])
print("結果形狀:", result.shape)  # 輸出: torch.Size([3, 2, 5])

三維張量與二維張量相乘（高維廣播）

# A: 批量大小為2，通道數為3，每個是4×5的矩陣
A = torch.randn(2, 3, 4, 5)  # 形狀: (2, 3, 4, 5)# B: 單個5×6的矩陣
B = torch.randn(5, 6)        # 形狀: (5, 6)# 廣播過程：
# 1. B補全維度: (5, 6) → (1, 1, 5, 6)
# 2. B擴展第一維: (1, 1, 5, 6) → (2, 1, 5, 6)
# 3. B擴展第二維: (2, 1, 5, 6) → (2, 3, 5, 6)
# 矩陣乘法: (2, 3, 4, 5) @ (2, 3, 5, 6) → (2, 3, 4, 6)
result = A @ B               # 結果形狀: (2, 3, 4, 6)print("A形狀:", A.shape)     # 輸出: torch.Size([2, 3, 4, 5])
print("B形狀:", B.shape)     # 輸出: torch.Size([5, 6])
print("結果形狀:", result.shape)  # 輸出: torch.Size([2, 3, 4, 6])