Graph Neural Network(GNN)

我們首先要了解什么是圖,圖是由節點和邊組成的,邊的不一樣也導致節點的不同(參考化學有機分子中的碳原子)

gnn可以處理classification的問題,也就是分類的問題

也可以處理generation的問題

借一部日劇來說明,這個日劇是講主角尋找殺害他父親的兇手的,劇中的人物有姓名和特征

假如我們已經有一些label,我們知道誰肯定不是兇手,將這些人的信息丟進model中,訓練model

但是,這是不夠的,每個角色的關系也是非常重要的

不過,我們想要運用gnn也有一些難點,我們怎么理順每個節點間的關系,考慮全局的情況,當這個圖變得很大的時候,我們怎么處理,如果我們不知道全部的label,我們該怎么辦

我們怎么用已知label的node?我們知道相連的節點間肯定存在著不為人知的關系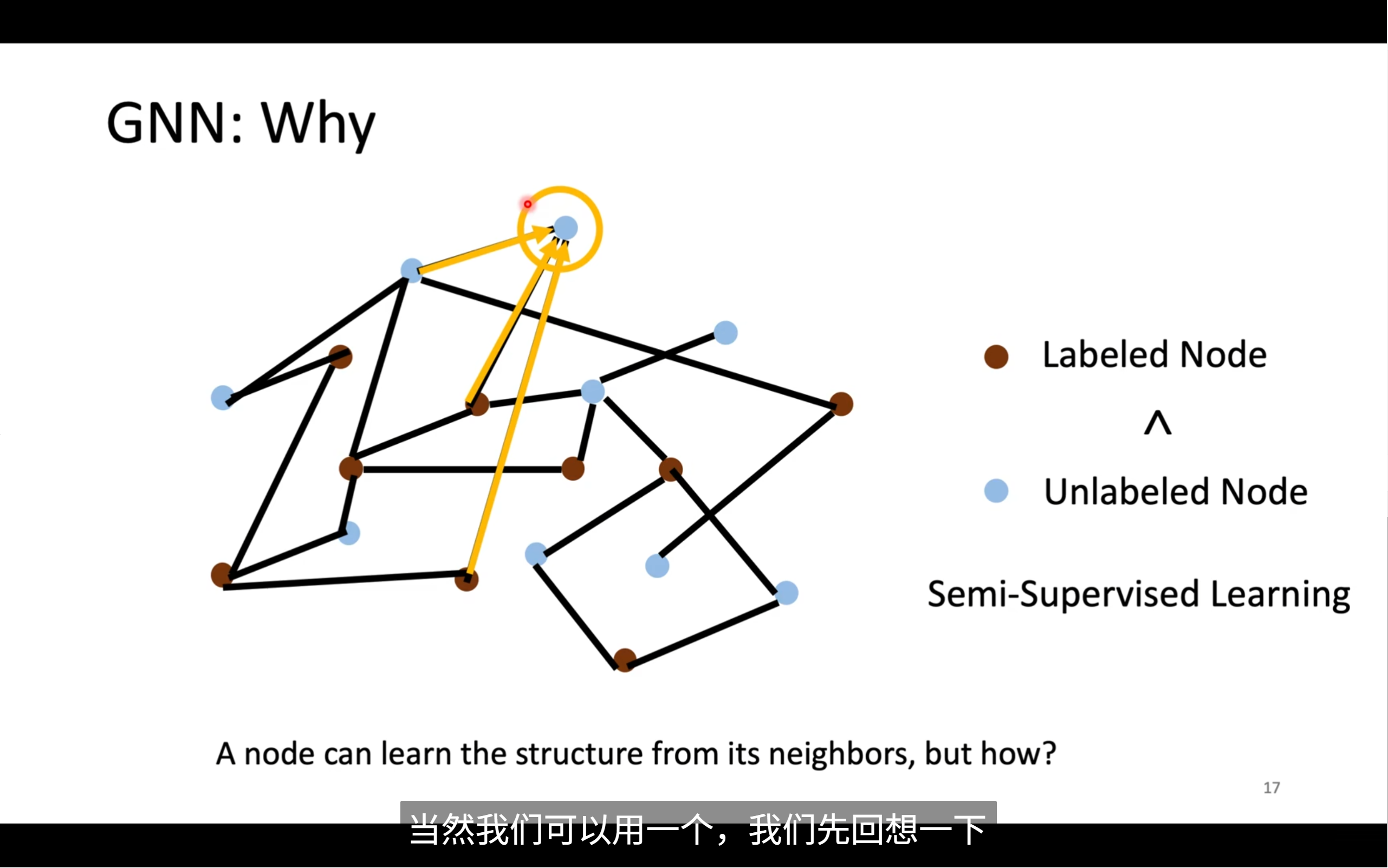

我們在cnn中知道我們做convolution使用卷積核在圖像上移動,通過相乘相加來得到一個kernel在區域內的值,也就是feature map,我們該如何將這個方法運用到gnn中呢?

首先來看convolution

🧭 圖譜：GNN Roadmap 總覽

這張圖從四個角度總結了 GNN 的發展路線：

🟨 1. 核心機制：Convolution（圖卷積）

GNN 的核心思想是：“將神經網絡中的卷積思想遷移到圖結構中”，對圖中節點進行了特征聚合。

圖卷積方法大致分為兩類：

Spatial-based（空間域方法）：從節點鄰接結構出發，直接對鄰居節點進行特征聚合
Spectral-based（頻譜域方法）：基于圖拉普拉斯分解引入傅里葉變換處理圖信號

🧩 2. 空間基 GNN（Spatial-based）

空間方法模擬“鄰居信息匯總”的過程，主要體現在不同的?Aggregation（聚合）策略?和對應方法：

Aggregation 類型	示例方法
Sum（求和）	NN4G（Neural Network for Graphs）
Mean（平均匯總）	DCNN, DGC, GraphSAGE
Weighted sum（加權求和）	MoNet, GAT（Graph Attention Network）, GIN（Graph Isomorphism Network）
LSTM 聚合（帶門控）	GraphSAGE（使用 LSTM 聚合鄰居）
Max Pooling（取鄰居最大值）	GraphSAGE

🧠 特別說明：

GraphSAGE?是一個靈活框架，支持多種聚合方式（Mean / LSTM / Pooling 等）
GAT?使用注意力機制決定各個鄰居對當前節點的“權重”
GIN?是表達能力最強的空間方法之一，理論上能判別最多非同構圖

🟧 3. 頻譜基 GNN（Spectral-based）

頻譜方法的核心來自圖信號處理，先用圖拉普拉斯矩陣對圖進行譜分解，再定義“卷積”。

主要發展路線如下：

ChebNet → GCN → HyperGCN

ChebNet：使用切比雪夫多項式逼近圖濾波器（更高階）
GCN（Graph Convolutional Network）：最經典的頻譜 GNN，使用局部一階逼近，簡潔高效
HyperGCN：將 GCN 推廣到超圖結構

🎯 頻譜方法優點是理論扎實，缺點是需要固定圖結構，難以泛化到新圖。

🧩 4. 任務（Tasks）：GNN常見應用方向

GNN 強大的表達能力使其適用于多種圖數據學習任務：

Supervised Classification：圖節點/圖整體的分類任務
Semi-supervised Learning：只給部分節點打標簽，GNN可以利用鄰居信息傳播標簽
Representation Learning：學習節點/圖的表示，如 Graph Contrastive Learning（Graph InfoMax）
Generation：生成新的圖結構，如：
- GraphVAE（基于 VAE 的圖生成）
- MolGAN（生成分子結構）

🔵 5. GNN 與 NLP 的結合（底部藍色部分）

“Application: Natural Language Processing”

GNN 在 NLP 中表現出強大的建模能力，因為語言中的很多結構天然可以表示為圖：

NLP結構	如何構圖
句法依存分析	構建?句法依存圖（詞作為節點，依存關系作為邊）
知識圖譜	實體為節點，關系為邊，一種典型異構圖
文檔建模	構建“文檔-詞”或者“詞-詞共現圖”
QA系統	通過 GNN 做 reasoning，對知識路徑建模
文本生成	用 GNN 學習長文本邏輯結構關系

經典方法如：

Text GCN
Heterogeneous GNN
GAT for tokens

🧠 圖中提到兩種理論分析方法：

🔶 頂部橙色部分提到了：

Theoretical analysis: GIN, GCN

說明：

GCN：頻譜理論代表作，奠定 GNN 理論的基礎
GIN：理論上能判別大多數圖的結構，表達能力最強

因此兩者處于理論分析的重要位置。

? 總結：這張圖告訴我們什么？

部分	內容	說明
💛 中間黃色	GNN 的核心機制是圖卷積（Spatial vs Spectral）
🟫 棕色框	Spatial 里的不同聚合策略和實例方法
🟧 桃色框	Spectral 的發展脈絡（ChebNet → GCN → HyperGCN）
? 綠色框	GNN 支持的主要 AI 任務
🔵 藍色框	GNN 在 NLP 中的重要應用方向

把convolution用在graph上有個區別,就是kernel原本是一個固定大小的kernel,但是圖中的kernel是根據節點的edge來變的,只會跟節點的鄰居有關

🧠 一、什么是 NN4G？

NN4G（Neural Network for Graphs）?是最早將神經網絡的思想用在圖結構數據上的一種方法。提出于 2009 年（論文鏈接見圖上），核心思想是：

通過多層感知機（MLP）的形式，把一個節點的鄰居特征棧起來輸入虛擬“神經元”，合成高層表達。

它可以看作 GNN 的雛形 💡，是圖神經網絡的鼻祖之一。

🧮 二、整體結構解析

圖中展示了圖神經網絡在某一節點 ( v_3 ) 上的前向傳播過程，分為三層結構：

🔸 Input Layer（輸入層）

節點表示如下所示，每個節點都有一個特征向量 ( \mathbf{x}_i )，比如：

x?, x?, x?, x?, x?

其中?x??是我們關注的節點 ( v? ) 的原始輸入特征。

🔹 Hidden Layer 0（隱藏層0）

對每個節點 ( v_i )，定義其在第0層的隱藏表示為： [ h_i^0 = \text{MLP}_0(x_i) ] 圖中藍色框表示 ( h_0^0, h_2^0, h_4^0 ) 是節點 ( v_3 ) 的鄰居在第0層的表示，紅色圓框圈出了這些鄰居節點。

這種在圖中根據邊連接找鄰居、獲取鄰居表示的操作，叫做：

鄰居特征聚合（Neighborhood Aggregation）

🔸 Hidden Layer 1（隱藏層1）

要生成節點 ( v_3 ) 的下一層表示 ( h_3^1 )，它由?兩部分信息組合而成：

📐 三、關鍵公式講解（圖右上角）：

[ h_3^1 = \widehat{W}_{1,0} \cdot (h_0^0 + h_2^0 + h_4^0) + \widehat{W}_1 \cdot x_3 ]

我們來逐塊解釋：

🟩 ① 聚合鄰居的隱藏表示總和：

[ (h_0^0 + h_2^0 + h_4^0) ] 代表節點 ( v_3 ) 的所有鄰居節點在 Hidden layer 0 的表示。

黃色點表示鄰居節點
紅色圈出了鄰接節點
藍框內是節點隱藏表示

🟩 ② 聚合鄰居后，乘以線性變換：

[ \widehat{W}_{1,0} \cdot ( \cdots ) ] 是一個可學習權重矩陣，對鄰居的聚合信息進行線性變換，類似于傳統神經網絡的?W·x

🟨 ③ 加上自身特征變換：

[

\widehat{W}_1 \cdot x_3 ] 也對節點本身的原始輸入特征做一次映射

? 整體理解：

“隱藏層新的狀態 = 聚合鄰居表征 + 本節點特征處理”

這個思想已經是現代 GNN 的共識，后來很多流行 GNN（GCN、GAT、GIN）都在這基礎上進行優化：

模型	提升方向
GCN	用歸一化、簡化計算，變成矩陣形式
GAT	通過注意力機制為不同鄰居賦予不同權重
GraphSAGE	把聚合策略做成模塊化（mean, max, LSTM 等）
GIN	理論上最強，有最大表達能力

🧭 圖中標注說明

圖中元素	含義
🟫 棕色節點?`v? ~ v?`	圖中的節點
🟨 黃色框?`x_i`	節點在輸入層的原始特征向量
🔵 藍色框?`h_i^0`	節點在第0層的隱藏層表示（由輸入計算得出）
🟥 紅色橢圓	當前節點 ( v? ) 的鄰居集合（準備聚合）
🟨+🟩 相加權公式	封裝了新的表示生成邏輯

🔍 用一句話來總結 NN4G：

NN4G 是將圖結構信息引入神經網絡最原始的方式 —— 它通過“鄰居求和 + 自身特征”的線性方式來構建節點的逐層表示。

? 后續你可以深入的方向：

手動實現 NN4G 的更新函數（用 PyTorch）
比較 NN4G 和 GCN 的異同
用小圖跑一遍 Forward Pass
引入非線性/Attention/歸一化，看看體驗提升

readout是怎么做的呢?

📌 類比記憶（便于理解）

你可以把整個過程想象成一個投票系統，每一層節點像一組專家：

第0層：只知道自己和鄰居，局部看問題
第1層：知道兩跳關系，有一定全局視角
第2層：更深，能看懂更多上下文

最終，我讓三組專家都說一句話，然后用自己設定的權重，綜合判斷這個圖怎么分類。

省略了兩個model,接下來的是用weighted sum方法的model,因為每個node的重要性是不一樣的,所以會有權重

🧠 MoNet 的核心思想是什么？

MoNet 是一種可以適配不同圖結構的通用圖神經網絡。相比傳統 GCN 的**“平均鄰居表示”**，它做了兩個關鍵改進：

? 1. 給每個鄰居一個?可學習的權重

不再簡單平均！而是根據鄰居與中心節點的相對結構關系計算權重。

? 2. 使用?偽坐標 (pseudo-coordinates)?來定義鄰居之間的關系

🧩 圖中公式的逐步講解

?1. 聚合操作（核心公式）

我們以節點 3 的更新公式（圖右上）為例：

h?1 = w(??,?) · h?? + w(??,?) · h?? + w(??,?) · h??

說明：

h?1：節點 3 在第 1 層的表示
h??, h??, h??：第 0 層時，節點 0、2、4 的表示（鄰居們）
w(??,?)：鄰接權重（表示節點 3 和節點 0 的關系，由神經網絡計算）
·：向量加權
所有鄰居的表示都乘上權重后求和，等價于帶權聚合

這是一個加權求和（weighted sum）動作，但權重由“距離函數”學習得到。

?2. 什么是?`??,y`？

MoNet 的權重函數是作用在“偽坐標”上的。這個偽坐標為：

u(x, y) = [ 1/√deg(x),   1/√deg(y) ]

說明：

deg(x)：節點 x 的度（鄰居數量）
所以它是一個 2 維向量，代表了邊 (x, y) 兩個點的局部結構情況

舉例：?如果：

節點 3 度數是 3
節點 0 度數是 2

那么：

u(3, 0) = [1/√3, 1/√2]

然后我們通過一個變換函數（比如一個 MLP）變成：

??,? = f(u(3, 0))   → 輸入偽坐標，輸出用于計算權重

?3. 權重函數怎么定義？

MoNet 使用一種高斯核 + 神經網絡的方法來定義權重，右下角的公式是核心：

Σ?y ∈ N(x)?  ∑?  e^(-0.5 · (?(x,y) - μ?)? Σ??1 (?(x,y) - μ?)) · f?(h_y)

我們拆解它：

?(x,y)：x 和 y 之間的偽坐標（高維）
μ?：某個核中心（高斯分布中心）
Σ?：核的協方差矩陣
f?(h_y)：對鄰居節點 y 的表示的映射（例如一個MLP）
最外層累加：將不同核的加權結果疊加

?解釋起來像什么？

它就是在說：

“我把相鄰節點 y 拿來，把它的距離（?）投給多個高斯核，然后根據這個概率來做加權，決定它對中心節點 x 的影響程度。”

🎨 圖示解讀補充（連圖一起復習）

🔵 圖中的內容含義總結：

圖中符號	含義
`h??`（藍色方塊）	節點 0 在 0 層時的特征
`h?1`（橙色方塊）	節點 3 在 1 層的特征（正在更新）
`u?,?`	節點 3 與節點 0 的邊的偽坐標
`w(??,?)`	神經網絡作用在偽坐標上的輸出權重
黃色點	是節點 3 的鄰居

? 總結 MoNet 的核心邏輯

步驟	描述
① 定義偽坐標?`u(x,y)`	利用節點度數、位置等，描述結構關系
② 定義權重函數?`w(?)`	可以用神經網絡對?`?`?建模
③ 加權聚合鄰居特征	權重 × 特征后求和，更新中心節點表示

? MoNet 的優勢

優勢	說明
?? 通用性強	可應用于圖結構、網格、點云等
?? 表達能力強	可學習的連續權重模型更細膩
?? 包含多個 GNN 的特例	特定情況下它可以約簡成 GCN、GAT 等

GAT是對每一個節點的鄰居做attention,它的weight是自己學出來的,來分辨鄰居對他的重要性

GIN

📌 MLP 是什么？

MLP 全稱是：Multi-Layer Perceptron，即?多層感知機，是最基礎也是最重要的一種神經網絡結構。

? 在 GNN/GNN 中，MLP 是個模塊/函數：

它的作用是：

把一個向量（比如節點的聚合特征）作為輸入，經過若干層?線性變換 + 激活函數，生成新的節點表示。

可以簡單表示為：

[ \text{MLP}(x) = \sigma(W_2 \cdot \sigma(W_1 \cdot x + b_1) + b_2) ]

x：輸入的向量
W_1, W_2：權重矩陣
b_1, b_2：偏置項
σ：激活函數（通常是 ReLU）

🧠 在 GIN 的公式中 MLP 的具體作用

首先看 GIN 的聚合和更新公式（圖上方）：

[ h_v^{(k)} = \text{MLP}^{(k)}\left( (1 + \epsilon^{(k)}) \cdot h_v^{(k-1)} + \sum_{u \in \mathcal{N}(v)} h_u^{(k-1)} \right) ]

我們逐部分拆開解釋：

? 1. 聚合（鄰居加和值）

[ \sum_{u \in \mathcal{N}(v)} h_u^{(k-1)} ]

意思是：把節點 v 的鄰居 u 的特征向量都加起來，不做平均、不做權重。

這是 GIN 的創新——使用 sum 聚合，對表示能力更強！

? 2. 加上自己的殘差：

[ (1 + \epsilon^{(k)}) \cdot h_v^{(k-1)} ]

這里的 ε 是一個可學習的參數（或固定為 0/1），用于控制保留多少“自己的信息”。

? 3. 輸入 MLP 做非線性映射：

[ \text{MLP}^{(k)}( \cdots ) ]

這一步才是真正更新后的節點表示?h_v^{(k)}，它相當于把“原始 + 鄰居特征的整合結果”映射到新空間中。

每一層的 MLP 可以是獨立的（擁有自己的一組參數），如下用 PyTorch 實現：

# 輸入維度 d_in，隱藏層 2 層，每層都有 ReLU 激活 import torch.nn as nn mlp = nn.Sequential( nn.Linear(d_in, hidden), nn.ReLU(), nn.Linear(hidden, d_out) )

🏗 舉個例子形象理解

你可以把 GIN 中的 MLP 理解為下面這個過程：

你聚合鄰居說話內容（特征向量加在一起）
加點你自己的聲音（殘差）
然后這些內容交給一個“智能變壓器”——MLP
這個變壓器幫你重新加工，變成新的一種表達（下一層特征）

🥇 為什么 GIN 要用 MLP？

作者（Xu et al., 2018）證明：

只有這樣一套設計（sum 聚合 + MLP 映射）才能擁有和 Weisfeiler-Lehman(Graph Isomorphism Test) 一樣強的判別能力！

? 總結

關鍵詞	含義
MLP	Multi-Layer Perceptron，多層感知機
作用	對聚合后的節點特征做非線性映射，提升模型表達能力
在 GIN 中的地位	必不可少，核心結構
與 GCN/GAT 不同	GCN 用線性映射，GIN 用 MLP 所以更強表達性

以上都是spatial based的convolution的方法,下面講的是很神奇的spectral based的方法

📘 Spectral-Based Convolution（頻譜圖卷積）- 通俗解析版

🔍 1. 什么是頻譜圖卷積？

在圖神經網絡中，頻譜卷積（Spectral Convolution）?是一種用“頻率”視角來處理圖上節點特征的方法。

它的核心思想是：

把圖上的節點特征信號變換到頻域，在頻率維度做濾波，再重新變回來。

這與音頻處理中的傅里葉變換非常相似。

🧠 2. 整體流程梳理

我們假設圖的一層節點特征是：

Layer i: h0, h1, h2, h3, h4 -> 原始節點的向量特征

我們用以下步驟來“做圖卷積”：

步驟 1：Graph Fourier Transform（圖傅里葉變換）

輸入節點特征 h 轉換為“頻率分量”
可以想象你提取出：高頻信息（變化劇烈），低頻信息（平滑）

步驟 2：頻域乘以 Filter（濾波器）

這個濾波器決定保留哪些頻率信號（就像音頻強調低音/高音）

步驟 3：Inverse Transform（逆變換）

把濾波后的頻率信息還原回原始節點空間
得到新的節點特征 h'

📐 3. 對于一個圖，怎么操作呢？

3.1 構造圖的 Laplacian 矩陣

圖的拉普拉斯矩陣 L 定義如下：

L = D - A

或者使用歸一化形式：

L = I - D^(-1/2) × A × D^(-1/2)

其中：

A 是鄰接矩陣（誰和誰有邊）
D 是度矩陣（每個節點連接了幾個點）
I 是單位矩陣

3.2 做特征值分解（Eigen Decomposition）

對拉普拉斯矩陣 L 分解成：

L = U × Λ × U^T

含義如下：

U 是一組正交向量矩陣（“頻率基底”）
Λ 是一個對角矩陣，表示每個頻率的強度

可以想象 U 類似于圖片/音頻信號中的“正弦波模式”。

3.3 圖傅里葉變換

用 U 把節點特征 h 轉換到頻域：

h_hat = U^T × h

h_hat 是每個頻率分量對應的權重。

3.4 應用濾波器

我們設計一個頻率濾波器 g，用它乘以譜域表示：

h_hat_filtered = g(Λ) × h_hat

這個乘法會對某些頻率加強、某些頻率減弱（比如保留低頻）。

3.5 逆變換回去

最后，我們把經過濾波的頻率信號變回節點特征：

h' = U × h_hat_filtered

這個 h' 就是 Layer i+1 層的新節點表示。

💬 4. 總結一下圖中的流程

圖中展示了從一層到下一層的過程：

Layer i (藍色) → Layer i+1 (橙色) ↓ ↑ Graph Fourier Transform Inverse Transform ↓ ↑ 頻率域表示 × 濾波器（例如一個 3x3 矩陣權值）

這就是頻譜法進行圖卷積操作的完整流程。

? 5. 優點 & 缺點對比

項目	優點 ?	缺點 ?
理論基礎	來源于圖信號處理系統，數學嚴謹	直觀性差，不容易解釋
濾波能力	可以嚴格控制信息流（高頻 / 低頻）	濾波器是全局的，對“局部鄰居”不敏感
適用范圍	在小圖、固定結構圖上表現很好	不支持動態圖 / 新圖泛化
計算成本	原理上是可控的頻率分析	拉普拉斯分解需要 O(n3)，不能用于大圖

? 6. 衍生版本（簡化頻譜 GNN 的方法）

由于原始譜卷積太復雜，下面這些方法是對它的高效版本改進：

模型	思想
ChebNet	用多項式（切比雪夫多項式）來“近似濾波器”，提升效率
GCN（Kipf）	截斷到一階近似，變成鄰居平均的操作，計算極快、效果穩定

🔚 總結金句

Spectral-based GNN 是一種用“頻域濾波”思想來設計圖卷積的方式，它繼承了信號處理的經典理論，但實際應用中通常會轉化為簡化形式（如 GCN）。

我們進一步理解圖傅里葉變換

? 目標：用“生活語言”+ 形象解釋，帶你讀懂圖傅里葉卷積的構建磚塊！

🧩 一、傅里葉變換到底是什么？

? 類比：語音中的“高頻”和“低頻”

想象你聽一段音樂，有低音（鼓聲），有高音（小提琴），它們疊加起來構成整段音樂。

傅里葉變換的本質就是：

把一個復雜“信號”（比如音樂）分解成很多純粹的“頻率波”相加得到的結果。

我們用一個“頻率眼鏡🔍”來觀察信號里的結構，看它“包含了哪些高低音”。

? 數字信號里也一樣

假設你有個連續點的信號：

信號：1 1 1 1 0 0 0 0

一看就是有“變化”
傅里葉變換會說：
- 它包含一個低頻分量（因為左邊四個一樣）
- 有一個邊緣突然變化 → 含高頻信號

所以：傅里葉變換 ≈ 用振動圖告訴你一個東西是平還是抖

? 拓展到“圖”上怎么辦呢？

普通傅里葉變換處理的是連續音頻波形
→ 圖就像復雜的結構化信號，它是離散但有連邊（結構）

我們想知道：

圖上節點的特征變化是“光滑”的，還是“很震蕩”的？

于是我們對“圖上的信號”（比如節點特征）也想做傅里葉分析，那就用下面這些數學工具！

📘 二、度矩陣 D 是什么？

非常簡單！

對于每個節點來說，它連接了幾個鄰居？

我們稱這個數量為“度數”Deg。

節點	鄰居	度數
A	B, C	2
B	A, C, D	3
C	A, B	2

我們會構造一個對角矩陣 D，比如上面的圖會變成：

D = 
[2, 0, 0]
[0, 3, 0]
[0, 0, 2]

行列都是節點
對角元素就是“每個節點的連邊數”
非對角部分全是 0 ?

📘 三、鄰接矩陣 A 是什么？

鄰接矩陣就是：

如果兩個節點有邊連接，填 1
沒連接就是 0

A =
[0 1 1]
[1 0 1]
[1 1 0]

這個結構就表示“誰和誰連著”，矩陣視角下的圖結構。

📘 四、拉普拉斯矩陣 L 是什么？

圖的核心符號來了！

我們用度矩陣 D 和鄰接矩陣 A 構造出一個矩陣 L：

L = D - A

也就是說：

自己度數（連邊多少） → 放在對角線
去掉其他連接關系 → 做差

它本質上是——

懲罰“你和鄰居差太多”的一個矩陣！

? 舉個具體例子：

D = [2, 0, 0] [0, 3, 0] [0, 0, 2] A = [0 1 1] [1 0 1] [1 1 0] ? L = D - A = [ 2 -1 -1 ] [-1 3 -1 ] [-1 -1 2 ]

這個矩陣是圖傅里葉分析的靈魂！

🧠 五、特征值分解（Eigen Decomposition）是啥？

你可以理解為：

把矩陣抽象成很多“方向 + 伸縮量”的集合

像把物體旋轉 → 拆解成“每個方向上”是什么形狀。

對于矩陣來說，分解成：

L = U × Λ × U^T

含義是：

U：圖的“頻率基底”，像音頻里的“正弦波”
Λ：每個頻率的權重 = 頻率“強度”
U^T：還原回原始空間的方法

U^T × h：就是“把節點特征投影到頻率空間”
Λ × （這個h）：就是“濾波”
U × (...) ：是把頻率信息還原成節點結構

? 六、整套流程順口溜（保姆級）：

💬 一句話：

圖 → 構造鄰接矩陣 A 和度矩陣 D
得到拉普拉斯矩陣 L = D - A
分解得到頻率基底：U，Λ
把節點特征 h 變到頻率空間：U^T × h
濾波器作用：乘 Λ 或 g(Λ)
再變回來：U × 上一步 → 得到 h'

? 七、總結一句話！

概念	通俗理解
度矩陣 D	每個節點有幾個朋友？
鄰接矩陣 A	誰和誰是朋友？
拉普拉斯矩陣 L	你和鄰居之間的“差異衡量”
特征分解	把圖的頻率結構提取出來
傅里葉變換	看哪些點“震蕩得多”

再具體講解一下鄰接矩陣是怎么表示節點間關系的

📘 什么是鄰接矩陣（Adjacency Matrix）？

鄰接矩陣用于表示圖中有哪些節點連在一起。是一個二維矩陣，每一行和每一列都對應同一個節點。

? 舉個圖的例子

假設我們有一個很簡單的無向圖，它有 4 個節點，編號為 0、1、2、3，并且結構如下：

圖結構： (0) / \ (1)-(2) | (3)

連接邊是：

節點 0 連著節點 1、2
節點 1 連著節點 0 和 2
節點 2 連著節點 0、1、3
節點 3 連著節點 2

🧱 它的鄰接矩陣 A 是：

我們創建一個 4×4 的矩陣，行列都代表節點編號。

0 1 2 3 ← 列（目標節點） A = [ ← 行（源節點） [ 0 1 1 0 ], # 節點0連了1和2 [ 1 0 1 0 ], # 節點1連了0和2 [ 1 1 0 1 ], # 節點2連了0,1,3 [ 0 0 1 0 ] # 節點3只連了2 ]

🔎 如何看這個矩陣？

你可以這樣記住：

A[i][j] = 1?表示節點?i 和 j 有連邊
A[i][j] = 0?表示?i 和 j 沒有連邊

比如：

A[0][1] = 1 → 節點 0 連了節點 1 ?
A[3][0] = 0 → 節點 3 沒連節點 0 ?
A[2][3] = 1 → 節點 2 連了節點 3 ?

因為圖是無向圖，所以鄰接矩陣是對稱的！

🧠 那“節點的特征表示”數據在哪？

題問得非常好！鄰接矩陣?只負責表示“結構”，
節點真正的?數值特征表示是什么，是另外一個矩陣 (X) —— 節點特征矩陣！

假設我們給每個節點一個特征向量

節點 0: 特征 = [1.0, 0.2] 節點 1: 特征 = [0.9, 0.1] 節點 2: 特征 = [0.3, 0.8] 節點 3: 特征 = [0.2, 0.5]

我們寫成矩陣：

X = [ [1.0, 0.2], # 節點 0 [0.9, 0.1], # 節點 1 [0.3, 0.8], # 節點 2 [0.2, 0.5] # 節點 3 ]

也就是說：

每一行是一個節點的特征
列表示這個特征的維度（可以是 2 維、5 維、100 維都行）

🔁 在 GNN 中我們怎么用這些？

在圖神經網絡里，我們常常做的是：

用鄰接矩陣 A 來“指導”節點之間互相傳遞表示（特征）

結構來源于 A（誰影響誰）
特征來源于 X（每個節點自身內容，比如文本、圖像等）

? 用最簡單的代碼說明

使用 PyTorch 簡化說明：

import torch # 鄰接矩陣 A（4個節點） A = torch.tensor([ [0, 1, 1, 0], [1, 0, 1, 0], [1, 1, 0, 1], [0, 0, 1, 0] ], dtype=torch.float32) # 節點特征 X（每個節點是2維向量） X = torch.tensor([ [1.0, 0.2], # 節點 0 [0.9, 0.1], # 節點 1 [0.3, 0.8], # 節點 2 [0.2, 0.5], # 節點 3 ]) # 簡單的圖卷積核心思想：A @ X output = A @ X print(output)

你會發現，它就是用鄰接矩陣，把鄰居特征“加”過來了！

🏁 最后一句話總結：

對象	表示什么
鄰接矩陣 A	表示圖結構：誰和誰相連
特征矩陣 X	表示節點內容（如每個節點標題、顏色、向量等）
A × X	就是用結構去聚合鄰居的節點特征（最基本 GCN 核心）

進一步理解傅里葉變換

📘 一、傅里葉變換的第一性問題：它想干啥？

用一句話說：

傅里葉變換（Fourier Transform）就是把你身邊“復雜的信號”分解成一組“簡潔的正弦波”來表達。

原始信號可能又高又低、快慢不一，看起來很復雜
傅里葉告訴我們：其實所有的復雜波形都可以看作一個個**“純頻率的波”**疊加得到

🎵 舉個通俗例子（一聽就懂）：

你聽一段音樂，感覺很復雜：

有小提琴 → 高頻
有大鼓 → 低頻
有人聲 → 中頻

你聽不出哪些部分有啥，但傅里葉變換可以“分析”出來每種頻率分量有多強。

📊 二、從信號圖像看傅里葉

🔶 假設你有這樣一個函數：

f(t) = 一段起伏變化的信號（比如語音、電壓、氣溫序列）

它是關于時間 t 的函數，如下圖（想象）：

     ^
f(t) |            (ˉˉˉ)      (ˉ)|         (ˉˉ)    (__)|    (___)+--------------------------→ t

你看它好像亂七八糟，但其實：

? 傅里葉告訴你：

這個 f(t)，其實是若干個不同頻率的正弦/余弦波疊加出來的！

也就是說：

f(t) ≈ a?·cos(w?·t) + a?·cos(w?·t) + a?·sin(w?·t) + ...

每個 cos(w·t) 是一段波（頻率為 w）
a 是振幅，表示這個頻率有多強
全部加在一起，就變成原始函數！

🔍 三、那傅里葉“變換”到底是什么？

傅里葉“變換”是個運算符號，它把函數從 “時間/空間域” 轉換到 “頻率域”。

? 數學表達：

如果：

f(t) 是一個實數函數

則它的傅里葉變換 F(ω) 定義為：

F(ω) = ∫( -∞ 到 ∞ ) f(t) · e^(-iωt) dt

解釋：

這是一個“投影”的過程，把 f(t) 投到復指數 (e^{-iωt}) 上
相當于問：“在頻率 ω 這一波上，有多少存在？”
得到所有 ω 對應的“存在感”后，就得到了頻域表達 (F(ω))

🧠 概念翻譯（不講復雜積分）：

🔁 還有逆變換！

你也能從頻率分量“還原”原圖：

f(t) = ∫( -∞ 到 ∞ ) F(ω) · e^(iωt) dω

? 四、傅里葉變換的幾種直觀“視角”

角度	描述
🎶 聲音分析	從時域變頻域，看哪些音高（頻率）最強
📷 圖像壓縮	看哪些空間頻率信息最有用
🌊 信號濾波	把高頻噪音濾掉，保留低頻“主體結構”
?? 系統模擬	看一個系統是對哪些頻率響應強（濾波器響應）

? 五、小例子：你真想試一試傅里葉變換的效果？

用 Python（僅 5 行代碼！）看看頻域長啥樣：

import numpy as np import matplotlib.pyplot as plt t = np.linspace(0, 1, 1000) signal = np.sin(2 * np.pi * 5 * t) + 0.5 * np.sin(2 * np.pi * 20 * t) freq = np.fft.fftfreq(len(t), t[1] - t[0]) fft_result = np.fft.fft(signal) plt.plot(freq[:500], np.abs(fft_result)[:500]) plt.title("頻率分布圖") plt.xlabel("頻率(Hz)") plt.ylabel("振幅") plt.show()

你會看到兩個頻率上有峰值：5Hz 和 20Hz，說明信號來自這兩個振動！

🧠 總結（一句話背下來）：

傅里葉變換就是把一個信號分解成頻率的組合，把“混音”變成“頻譜”，就像給嗓音做頻率分析一樣！

? 你現在知道的：

名詞	通俗解釋
時域 (f(t))	就是原始數據隨時間變化的樣子
頻域 (F(ω))	就是告訴你“有哪些頻率組成了這個信號”
傅里葉變換	從時域 → 頻域
逆變換	從頻域 → 時域
正弦/余弦波	就是最基本的高頻/低頻振動單位，傅里葉的“積木”

在信號與系統中,當然,也在數學中

我們用合成與分析來進行傅里葉變換

📘 N-dim Vector Space（N維向量空間）

🌟 一、這張圖講的是什么？

這張圖討論的是：

在一個 N 維空間中，任何向量（A）都可以表示為一組“基底”的加權和。

就像：你可以用“【上下】【左右】”這兩個方向，來表示地圖上的任意一點。

? 圖中三個公式解釋如下：

🟢 1?? 合成公式（構建一個向量）

A = ∑(k = 1 到 N) [ a_k × v?_k ]

翻譯成中文：

向量 A?是由?N 個基底向量 v_k，乘上它們各自的系數 a_k，最后加起來組成的。我們稱這組 v_k 是一組“基底（basis）”。

🔸 舉個例子（二維）：

A = [3, 4]  
= 3 × [1, 0] + 4 × [0, 1]  
→ 用 x 軸上的單位向量 + y 軸上的單位向量，來合成整個 A。

這就是 “合成”。

🟣 2?? 分析公式（如何計算每個系數）

a_j = A · v?_j

翻譯：

想知道 “A 在第 j 個方向上的強度”，只需要求 A 與第 j 個基底向量的點積。

也就是說：

如果你手上有一個向量
想知道它“在某個方向上有多大分量”
就用點乘（dot product）去計算

🔵 3?? 正交公式（基底之間互不打架）

v?_i · v?_j = δ_ij   （δ_ij 是克羅內克δ）

含義：

當 i = j → 點乘結果 = 1
當 i ≠ j → 點乘結果 = 0

這是說：

一組好的基底向量彼此之間是正交的（垂直的），它們互相沒有“混疊”，獨立純粹。

這在傅里葉變換中特別重要：

不同頻率 = 不同的方向
用一組正交波形（正弦、余弦）來表示所有信號
所以傅里葉基底是“正交基底”

? 圖中合成 & 分析的對比

概念	對應公式	含義
合成（Synthesis）	A = ∑ a_k · v_k	把基底拼在一起組成向量 A
分析（Analysis）	a_k = A · v_k	把向量 A 拆到每個基底方向上的強度
正交性	v_i · v_j = 0（i ≠ j）	每個方向不會影響另一個方向

🔄 類比到傅里葉變換（連接頻域的核心）

向量范疇	傅里葉范疇
向量 A	時域信號 f(t)
基底 vector v_k	正弦波 e^(iωt)（頻率基底）
系數 a_k	頻率分量 F(ω)
合成公式	f(t) = ∑ F(ω) × e^(iωt)
正交性	正弦/余弦之間也是正交的

🎯 用一張圖總結

      ←---------------------------→
時域信號 f(t)     ←→     頻域分量 F(ω)合成                              分析??                                   ??∑ a_k·v_k        ←        Dot Product（拼成向量）               （拆分方向強度）

? 總結一句話

向量空間中的“分析”、“合成”思想，就是傅里葉變換的數學基礎！

把信號 f(t) 看作一個向量
把頻率波形 e^(iωt) 看作一組正交基底
傅里葉變換 = 分析信號“投影到各頻率”的大小
傅里葉逆變換 = 合成出完整信號

接下來是

🧠 本頁要講解的是：構建譜圖卷積中的圖結構數據

🎯 1. 什么是 Graph G = (V, E)

這個是圖的基本定義：

V?是圖的節點集合（比如人、人、城市）
E?是圖的邊集合（誰和誰有關系）
N = |V|?表示節點數量，例如有 5 個節點 → N = 5

📦 2. 鄰接矩陣 A ∈ ????

我們用一個矩陣?A?來表示圖的結構（也叫權重矩陣、Adjacency Matrix）。

A[i][j] = 邊 (i, j) 的權重

圖中定義了：

A[i][j] = { 0 如果 i 和 j 之間沒邊 w(i, j) 如果 i 和 j 之間有邊（權重） }

如果是無權圖，我們一般寫成 1 表示有邊
如果是加權圖，用?w(i, j)?表示邊的權重值

? 特別說明：

圖中說：

We only consider?undirected graphs

也就是說：

A[i][j] = A[j][i]
鄰接矩陣是對稱的！

🔢 3. 度矩陣 D ∈ ????

Degree Matrix，表示的是每個節點“有幾個鄰居”。

D[i][i] = d(i) = 節點 i 的度數（跟幾個人連接） D[i][j] = 0 如果 i ≠ j （非對角線全 0）

也就是說：

度矩陣是一個對角矩陣，每個對角線元素的值等于該節點的度數（即 A 的每一行之和）

? 公式解釋：

D[i][j] = { d(i), 如果 i == j （對角線） 0, 否則 }

你可以把它想象成：

D = diag([度數0, 度數1, ..., 度數N])

📊 4. 圖上的信號 f : V → ??

這句話特別關鍵！

把圖上的每個?節點?都賦一個?數值信號（特征）。

比如：

節點 i	f(i) 表示
0	溫度 = 25℃
1	文本情感值 = 0.8
2	像素強度 = 135

我們用一個函數：

f : V → ?

或者記作一個向量：

f = [f(0), f(1), f(2), ..., f(N-1)]

🔁 🧠 總結一下這頁討論的核心元素

符號	含義
G = (V, E)	圖結構（節點 + 邊）
N	節點數量
A	鄰接矩陣（結構連接關系）
D	度矩陣（每行度數）
f(i)	圖上每個節點攜帶的特征或信號

這些元素是譜圖卷積中建模圖結構的“數學基礎”，后面你就會看到拉普拉斯矩陣、傅里葉變換等都會基于這些計算。

?? 后面會涉及的概念預告（幫你銜接理解）：

下一步，我們會使用：

A 和 D 來構造?圖拉普拉斯矩陣 L?：L = D - A
然后用 L 做特征分解，做圖傅里葉變換
實現圖神經網絡中的頻域卷積（如 ChebNet, GCN 等）

📘 圖譜理論中的核心知識點：Graph Laplacian 的光譜分解

? 1. 圖拉普拉斯矩陣：L = D - A

這是譜方法中最基礎的一步：

A?是鄰接矩陣，用于表示每對節點之間有沒有連邊
D?是度矩陣，每個對角線元素是某節點的度（連接數）
L = D ? A?被稱為非歸一化拉普拉斯矩陣

它本質上在做什么？

表示“一個節點和它的鄰居有多不一樣”的結構度量。

? 2. L 是對稱矩陣（symmetric）

如果圖是?無向的（Undirected Graph），那么 A 是對稱的，因此 L = D - A 也是對稱矩陣。

對稱矩陣有哪些好處？

一定可以被特征值分解
有一組正交的特征向量作為基底

這為后面進行傅里葉變換做鋪墊！

? 3. 光譜分解：L = U × Λ × U?

這是最關鍵的一步，也叫譜分解，或者特征值分解。

你可以把它理解為對這個“圖的結構矩陣”進行“頻譜分析”。

U?是由 L 的特征向量組成（每一列是一個特征向量）
Λ?是對應的特征值，排成一個對角矩陣（對角線上是 λ）

📌 數學上講： [ L \cdot u_k = \lambda_k \cdot u_k ] 也就是說：每個 ( u_k ) 是 L 的一個特征向量，對應特征值 ( \lambda_k )

一個特征值 λ_k 對應一個頻率

一個特征向量 u_k 就是“這個頻率方向上的基底”

? 4. 矩陣符號說明

符號	含義
Λ（Lambda）	一個對角矩陣，對角線上是特征值 λ?, λ?,...
U	N×N 的矩陣，每一列是 L 的特征向量 ( u_0, u_1, ..., u_{N-1} )
U?	U 的轉置，作為還原操作（就像傅里葉逆變換）
L	拉普拉斯矩陣，通過 U 和 Λ 組合可以還原出來

? 5. 可視化解釋圖（下方彩色方塊）

這個圖像表達的是：

L = U × Λ × U?

可以類比如下操作：

復雜圖 L → （解構）→ 頻率空間（Λ）+ 基底方向（U） → → 再還原回來（U?）

黃色方塊（L）：復雜原始數據（表示節點之間的結構關系）
中間藍綠藍（U * Λ * U?）：對它進行分解為頻率分量（Λ），各方向上的響應（U）

🧠 特征值 λ 與“頻率”的直覺理解：

λ 小 → 平滑的特征 → 類似于低頻（變化不大）
λ 大 → 抖動劇烈的特征 → 類似于高頻（變化大）

圖傅里葉變換就是：

用?U? × f?把節點特征投影到這些“頻率維度”上，分析其中成分。

📌 最后一行結論

λ? 是一個特征值（frequency），
u? 是它對應的特征向量（frequency direction）

正如：

在普通傅里葉中：頻率 = 1Hz, 2Hz, ..., 震動方向 = cos(ωt), sin(ωt)
在圖信號中：頻率 = λ，振蕩模式 = u?

📋 總結表格

項目	含義	類比于普通傅里葉中
L	圖結構的整體拉普拉斯矩陣	f(t) 的二階導數結構
U	圖的“基底向量”	正弦波 / 復指數函數 e^(iωt)
Λ	圖的頻率分量（特征值）	各頻率大小 ω2
a? = U? · f	投影到頻域的系數	Fourier Coefficients

🙋 快問快答（幫你理解更牢）

Q1：為什么我們要做這個分解？

→ 把圖信號投影到頻率空間上（做濾波、分析）

Q2：為啥 L 可以被這樣分解？

→ 因為 L 是實對稱矩陣（性質好），所以一定能特征值分解

Q3：U 和傅里葉基底有什么關系？

→ 就是圖上的傅里葉基，定義的是“節點之間的振動模式”

就象是這樣的

圖譜理論

能量差異越大,頻率也就越大

💡 圖信號的平滑度 (smoothness) 與拉普拉斯算子

這張圖解釋的是如何通過圖拉普拉斯矩陣?L?計算圖信號的“抖動程度”或“變化強度”，
也就是《圖傅里葉變換》和《圖神經網絡》中信號處理的基礎！

📌 總體目標：

探索圖信號在圖結構下的“變化程度”：

變化劇烈（高頻） → 信號不平滑
差異小（低頻） → 信號平滑

最后我們會看到這個關鍵詞：

(1/2) × ∑∑ w_ij × [f(v_i) - f(v_j)]2

它測量了：所有邊上兩個節點的值差異之“平方和加權平均”——就是圖信號的“粗糙程度”。

🧠 我們從第一行開始分解說明：

? 第 1 行

(Lf)(v?) = ∑(v? ∈ V) w?? · (f(v?) - f(v?))

這表示對于圖中的每個節點 (v?)，圖拉普拉斯作用在函數 f 上的值，是：

自己和鄰居之間的一種加權差值和
( w_{ij} ) 是節點 i 和 j 之間的邊權（出自鄰接矩陣 A）

從圖濾波的角度，它表示“當前節點與鄰居節點值的偏差總量”。

? 第 2 行：寫成整體的矩陣二次型形式

f?·L·f = ∑(v? ∈ V) f(v?) × ∑(v? ∈ V) w?? (f(v?) - f(v?))

這是更常見的譜空間內寫法，表示的是“信號 f 在結構 L 下的變異度”。

? 第 3 行：展開乘法

把每一項的乘法乘進去：

= ∑∑ w?? × (f(v?)2 - f(v?)·f(v?))

? 第 4 行：對稱性合并項，乘 (1/2)

這個是技巧，只適用于?無向圖（對稱情況）：

= 1/2 × ∑∑ w?? × [f(v?)2 - f(v?)f(v?) + f(v?)2 - f(v?)f(v?)]

? 第 5 行：最終簡化公式???

= 1/2 × ∑∑ w?? × (f(v?) ? f(v?))2

這就是最重要的一步：

? 它表示信號在圖結構上的總變化程度（能量）
即：兩個連接節點之間，數值差得越多，代表圖信號變化劇烈

🧮 通俗總結就是：

圖結構上：

如果兩點連得近（大 w??）但值差很多 → 懲罰很大
如果兩點連得近但值差不多 → 懲罰小

→ 所以這個式子是一個“圖信號的光滑度量 / 不一致程度量”。

📊 信號平滑舉例：

節點對	f(vi)	f(vj)	差的平方	權重 w??	加權項貢獻
A-B	5	5	0	1	0
C-D	5	0	25	1	25

→ smooth 的信號在一條邊上變化小，值更小。

🟩 為什么這重要？

在圖神經網絡中，我們希望：

學到的特征 f 不要在圖上亂跳動
它要盡量“隨著連接關系而變化平滑”

所以這個公式就非常重要，用來衡量：

GCN 中信息傳播的平滑化本質
圖傅里葉中濾波器行為
圖正則化（Graph Laplacian Regularization）

? 數學 vs 直覺總結對照表

符號部分	通俗直覺
f?Lf	信號在圖結構中的粗糙度
(Lf)(v?)	點 vi 的“變化趨勢"
∑∑ w??(f? ? f?)2	所有“邊上差異”的總能量
權重大但值差 → 懲罰大	更不平滑，更高頻

? 最后一整句話總結

圖拉普拉斯作用于信號 f （f?Lf）衡量了信號在圖結構中“跳動”的大小。
它越小，說明信號越平滑，越是沿著圖結構自然傳播或變化的。

對于這個特征值(λ)和我們的頻率之間的關系

? 簡單一句話：

在譜圖理論中，λ 是特征值（eigenvalue），它表示信號在圖結構上變化的“幅度”或“頻率”。

🧠 圖結構中的 λ 是一種“頻率尺度”

再多解釋一點：

在傅里葉變換中，我們把一個信號（函數）表示為很多不同頻率的正弦波的疊加
在圖上沒有正弦波了，我們用特征向量?u??來代替“頻率基”
對應的 λ? 就是這個“頻率基”對應的頻率強度

🔍 圖中內容逐行講解

? 第一行公式是什么？

公式如下：

uiT?L?ui=λiuiT??L?ui?=λi?

這是標準的特征值定義：

你試圖在某個方向 u? 上施加圖拉普拉斯變換（L），

看它會乘上一個比例因子多少 —— 這個比例就是 λ?。

你可以理解為：

u?：某個“震蕩/振動”的方向（圖上的基底）
λ?：這個振動基底的“頻率能量大小”

小 λ ? 平滑（低頻）

大 λ ? 抖動明顯（高頻）

? 第二行英文解釋：

The eigenvectors corresponding to small λ belong to the low-pass part of a graph signal.

意思是：

小 λ 對應的特征向量 u 表示的是圖信號中“變化較小”（很平滑、低頻）的部分。

也就是說——在圖上傳播得越“順”，λ 越小；變化越突然（比如兩個連的點，值差很大），λ 越大。

📊 表格解釋

λ（特征值）	所代表的頻率	對應的特征向量?`u`	圖中信號示意
λ = 0	最小頻率（平滑）	`[0.5, 0.5, 0.5, 0.5]?`	所有節點值一樣（DC 分量）
λ = 1	低頻	`[?0.41, 0, ?0.41, 0.82]?`	僅輕微起伏
λ = 3	高頻	`[0.71, 0, ?0.71, 0]?`	一端高一端低（變化劇烈）
λ = 4	最高頻率	`[?0.29, 0.87, ?0.29, ?0.29]?`	中間瘋狂震蕩（像鋸齒）

🔍 圖下方圖示解釋

這些橙色垂直線表示：

每一列 u? 是一個長度為節點數的向量，每個數值表示一個節點的“振動強度”

你可以把它想成圖上的一個振動模式：

所有 u? 的值一致 → 沒有起伏（DC成分）
逐漸變化 → 低頻
左右跳躍、正負交替 → 高頻

🧠 類比到普通傅里葉

普通傅里葉變換	圖傅里葉（譜圖理論）
正弦波 sin(ωt)	特征向量 u?（圖上的“頻率波”）
頻率 ω? > ω?	特征值 λ? > λ?
頻率越高 ? 震動越快	λ 越大 → 信號在圖上起伏越劇烈

🔚 總結一句話：

λ 是圖結構的“頻率”，u 是頻率的“形狀”，f·u 就能得到你的圖信號在這個頻率方向上有多強。

在圖神經網絡中，我們常常：

用 λ 控制圖卷積要保留“低頻”還是“高頻”
用 u? 來對信號做傅里葉變換
λ 越小 → 表明方向越“平滑”，適合做平滑卷積
λ 越大 → 方向抖動大，感覺像“噪聲通道”

🎁 補充圖示記憶法 🎨

λ = 0 → －－－（全部一樣） λ = 1 → ／＼／＼（起伏輕微） λ = 3 → －v－^－（左右翻轉感） λ = N-1 → －^－v^－（變化頻繁，高頻）

對于這個圖傅里葉變換來說

x?是圖上每個節點對應的原始特征（信號）
U?是圖的“頻率基底”（Laplacian 的特征向量矩陣）
x??就是頻率空間下的圖信號，通過逐個特征向量?u??點乘?x?得到
把 x 投影到各個震蕩方向上，得分解強度

每一行：`u? · x`?表示什么？

就是圖信號在第 k 個頻率方向（特征向量 u?）上的分量有多強！

對應左邊那列紫色標簽：

u? ? x   → 低頻
u? ? x   → 中低頻
u? ? x   → 中高頻
u? ? x   → 高頻（震蕩很大）

小 λ 對應的頻率低，圖信號“平滑”
大 λ 對應的頻率高，圖信號“變化大”

圖傅里葉逆變換：

x=U?x^x=U?x^

把不同頻率方向上的振動強度組合還原，回到原圖信號
就是紫色頻譜反向合成橙色原始向量

? 左下角：（圖譜空間 x? 的直覺圖）

你可以看到橫軸是 λ（頻率），縱軸是信號?x?在每個頻率基 u? 上的投影大小：u? · f?

這張小圖就告訴你信號中含有多少“低頻”、“高頻”成分。

? 中下圖（圖上的原始信號）

在圖結構上，每個節點都有一個信號值：

f(v0), f(v1), f(v2), f(v3)

這些就是我們一開始的輸入信號向量?x

? 右上角（普通傅里葉對比）

上圖：

原始波形函數：f(t) 的時間序列
下圖：
- 把 f(t) 投影到不同頻率之后的頻譜圖
- 每個向量 a? = f(t) 投影到 sin/cos 頻率空間上

圖傅里葉做的和這個一模一樣：

只是把 sin() 替換成 u?（特征向量）

🤔 用圖上數據做個直覺小例子

假設你圖上有 4 個節點：

x = [1, 2, 2, 1]

意思是：

v? = 1
v? = 2
v? = 2
v? = 1

這個信號很平滑（中間比邊上高），你變換后會看到它在低頻 λ?, λ?上有很大能量，而在高頻 λ?上沒有多少。

? 最終總結金句：

圖傅里葉變換是把圖信號投到“結構頻率”的空間，讓我們分析它是平滑還是震蕩。

這個頻率空間是由拉普拉斯矩陣的特征向量?u??決定的，

? 圖中概念關鍵詞解讀：

項目	含義
x	圖信號（每個節點的數值）
U	圖的特征向量矩陣（頻率基底）
x?	圖信號在頻率空間下的表達
U?·x	圖傅里葉變換（分析）
U·x?	圖傅里葉逆變換（還原）

然后就是圖傅里葉逆變換

我們將頻譜中的頻率信號乘上一個對角矩陣,也就是機器要去學習的,得到yhead,這就是filter的原理

我們要將頻譜中的信號重新轉到圖信號,所以

最終這個方法可以總結成

但會造成一些問題,比如說對g的選擇會影響L,節點的大小也會影響model大小,并不像cnn一樣,不管圖片是多大,model的大小是一樣的,還有第二個問題,比如說g就是cosL,泰勒展開后會有L的N次方

L·x?→ 融合了一階鄰居
L2·x?→ 相當于走了 2 步，考慮的是二階鄰居
L3·x?→ 考慮三階鄰居
...
L^N·x?→ 所有節點都會影響所有節點（全局信息傳遞

ChebNet可以解決信號在全局的問題

但這個net的問題在于時間復雜度太高了,那么怎么降低呢,可以用一個遞歸的函數

然后我們就可以將x替換,得到下圖中的式子

進行這個轉換的原因是為了讓計算簡單,就像下面數學題

接下來是數學推導

我們當然可以learn出來幾個filter

GCN是最受歡迎的model

L是歸一化后地矩陣,最大特征值是2

? 最終把整個 GCN 你可以這樣理解：

步驟	做了什么
A? + D?	處理圖結構（誰和誰有邊、還包括自己）
歸一化	確保鄰居平均傳播，不影響不同節點度數
H^{(l)} × W	相當于全連接層
σ(...)	激活函數加非線性

🧠 總結記憶：

GCN = 鄰居信息平均 + 網絡權重投影 + 非線性

? GCN 的好處

優點	含義
💡 局部化傳播	每一層只看一階鄰居，結構清晰可解釋
?? 高效	不需要計算譜分解，沒有 UΛU?
💪 可遷移	可以泛化到任意圖結構，不固定拉普拉斯