反思

首先，先悔恨一下這次的比賽成績。

這次比賽的教訓就是，簡單的題目一定要打不要被復雜的題面震懾到，以及變量名不能是保留字，如第一題的x1,y1，要開long long，計算好數據范圍，如第三第四題。

T1

代碼思路

??????? 暴力枚舉寶石礦邊上的每一個點（整數，且是邊上的點，顯而易見邊上的點一定比中間的點要近），找出最小值排序輸出即可；注意小數精度問題。

AC代碼

#include<bits/stdc++.h>
using namespace std;const int N = 1e6+10;
struct Node{double xx,yy;
}a[N];
int xx1,yy1,x22,yy2,n,id; double func(double xx,double yy){double minn = 1e9;for(int i = xx1; i <= x22; i++){minn = min(minn,sqrt(pow(i-xx,2)+pow(yy1-yy,2)));}for(int i = xx1; i <= x22; i++){minn = min(minn,sqrt(pow(i-xx,2)+pow(yy2-yy,2)));}for(int i = yy1; i <= yy2; i++){minn = min(minn,sqrt(pow(xx1-xx,2)+pow(i-yy,2)));}for(int i = yy1; i <= yy2; i++){minn = min(minn,sqrt(pow(x22-xx,2)+pow(i-yy,2)));}return minn;
}int main(){freopen("cow.in","r",stdin);freopen("cow.out","w",stdout);ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);double mn = 1e9;cin >> n >> xx1 >> yy1 >> x22 >> yy2;for(int i = 1; i <= n; i++){cin >> a[i].xx >> a[i].yy;}for(int i = 1; i <= n; i++){double nw = func(a[i].xx,a[i].yy);if(nw < mn){mn = nw;id = i;}printf("%.9lf ",nw);}printf("\n%d",id);return 0;
} 

T2

代碼思路

??????? 首先講一下如何處理操作1,2，就拿map存每個數出現的次數，存加去減即可。

??????? 然后預處理1e5以內的數的因數是哪些，循環遍歷x的因數，看看map中是否存在，再計算出最大的k即可。

代碼

#include<bits/stdc++.h> 
using namespace std;const int N = 1e5+10; map<int,int> mp; //出現次數 
vector<vector<int>> a(N); //存因數 void init(){for(int i = 1; i <= N; i++){for(int j = i; j <= N; j += i){a[j].push_back(i);}}
}int mx_k(int d,int x){if(d == 1) return 0;int k = 0;while(x%d == 0){x/=d;k++;}return k;
}int query(int x){int mxx = 0;for(int i = 0; i < a[x].size(); i++){int d = a[x][i];if(d == 1) continue;if(mp.find(d) != mp.end() && mp[d] > 0){int k = mx_k(d,x);if(k > mxx){mxx = k;}}}return mxx;
}int main() {freopen("set.in","r",stdin);freopen("set.out","w",stdout);ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);init();int n,q;cin >> n >> q;for(int i = 1; i <= n; i++){int x; cin >> x;mp[x]++;}while(q--){int op,x;cin >> op >> x;if(op == 1) mp[x]--;else if(op == 2) mp[x]++;else cout << query(x) << endl;}return 0;
}

T3

代碼思路

?????? 按照題意建邊即可，但是第二個建邊要求直接暴力會超時，思考一下，可以直接建i到i-1的邊跑dijkstra就行了。還要注意數據范圍開2e6+10即可。

代碼

#include<bits/stdc++.h>
using namespace std;typedef pair<int,int> PII;
const int N =2e6+10;
int h[N],e[N],ne[N],w[N],idx,dist[N];
int n,m;
bool s[N];void add(int a,int b,int c){e[idx] = b;w[idx] = c;ne[idx] = h[a];h[a] = idx;idx++;
} void dijkstra(int st){memset(dist,0x3f,sizeof dist);memset(s,0,sizeof s);dist[st] = 0;priority_queue<PII,vector<PII>,greater<PII> > heap;heap.push({dist[st],st});while(!heap.empty()){auto t = heap.top();heap.pop();int k = t.second,dis = t.first;if(s[k]) continue;s[k] = 1;for(int i = h[k]; i != -1; i = ne[i]){int j = e[i];if(!s[j]){if(dist[j] > dis+w[i]){dist[j] = dis+w[i];heap.push({dist[j],j});}}}}
}int main(){freopen("paths.in","r",stdin);freopen("paths.out","w",stdout);ios::sync_with_stdio(0),cin.tie(0),cout.tie(0); memset(h,-1,sizeof h);cin >> n >> m;for(int i = 1; i < n; i++){int j = i+1;add(i,j,abs(i-j)),add(j,i,abs(i-j));}for(int i = 1; i <= m; i++){int a,b,z; cin >> a >> b >> z;add(a,b,z),add(b,a,z);}dijkstra(1);for(int i = 2; i <= n; i++){cout << dist[i] << " ";}return 0;
} 

T4

代碼思路

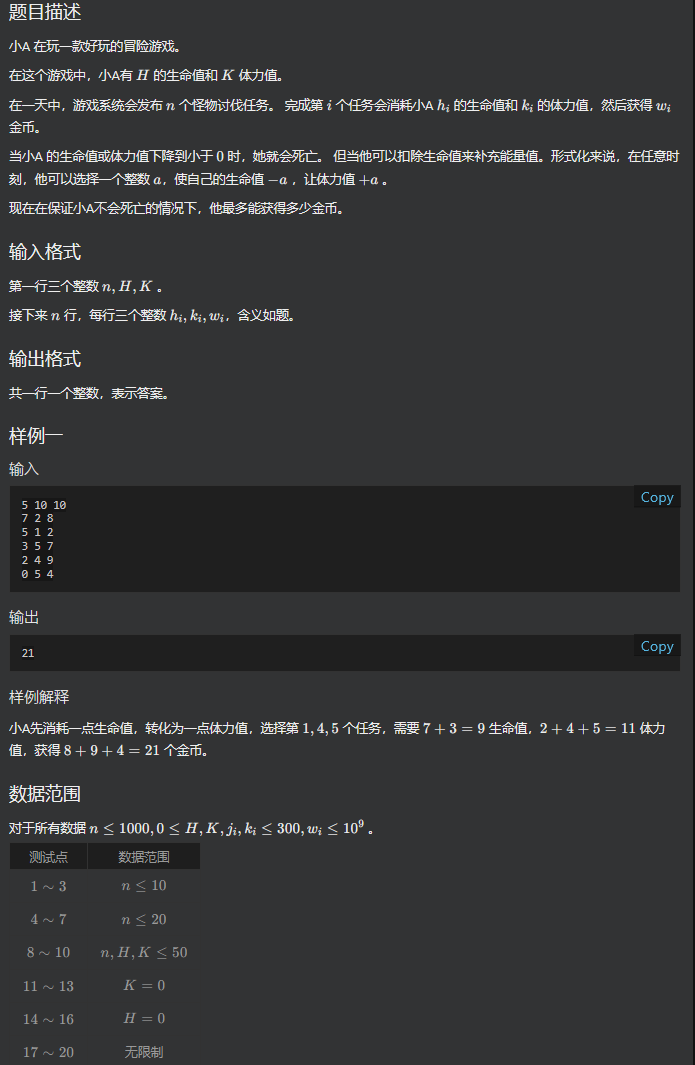
??????? 很明顯是個dp思路因為要分階段求最優方案，我們可以看成01背包，因為每個任務只能做一次，而“總背包空間”就是兩重約束，其中多余的生命值可以轉化為體力值。之后正常dp即可，要注意最優方案我們需要從0枚舉到生命值，以及0到體力值+剩余生命值，的最大值即可，還要開long long。

代碼

#include<bits/stdc++.h>
using namespace std;int n,H,K; 
const int N = 1e3+10;
long long k[N],w[N],h[N],dp[N][N];int main(){freopen("adventure.in","r",stdin);freopen("adventure.out","w",stdout);ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin >> n >> H >> K;for(int i = 1; i <= n; i++) cin >> h[i] >> k[i] >> w[i];for(int i = 1; i <= n; i++){for(int j = H; j >= h[i]; j--){for(int f = H+K-j; f >= k[i]; f--){dp[j][f] = max(dp[j][f],dp[j-h[i]][f-k[i]]+w[i]);}}}long long mxx = -1e9;for(int i = 0; i <= H; i++){for(int j =0; j <= H+K-i; j++){
//			cout << dp[i][j] << " ";mxx = max(mxx,dp[i][j]);}
//		cout << endl;}cout << mxx << endl;return 0;
} 

繼續努力，加油！！