一、目的

掌握Matlab中函數求導、函數極值和極限問題的求解,能夠借助Matlab工具對簡單優化模型進行求解。

二、內容與設計思想

1、函數求導

1.1求解給定函數的一階導數：diff(y, x)用于對變量x求y的導數。
1.2求解給定函數的二階導數：在求出一階導數的基礎上對其進行再次求導，得出二階導數。
1.3求解隱函數的導數
首先，通過定義符號變量建立隱函數模型。然后，使用diff函數對隱函數進行求導，得到一階導數和二階導數。再使用simplify函數簡化導數表達式，使結果更為直觀。最后，使用subs函數代入特定點的坐標，求解導數的實際值。

2、函數極值

2.1一元函數極值
1）先計算函數的一階導數，并解出一階導數等于零的所有點。由于題目要求區間 [-5, 1] 內的極值點，所以篩選掉了不在這個范圍內的點。然后，計算所有有效極值點的函數值，并從中找到了最小的那個。最后打印這個最小值。
2）首先定義了總成本函數C(q)，然后基于這個函數構造了平均成本函數A(q)。接著，它計算了平均成本函數的一階導數，并設置這個導數等于零來找到極值點。最后，它求解了這個方程，并輸出了解析出來的產量q的值，這是使得平均成本達到最小的生產量。
2.2多元函數極值
initial = [0, 0];設定優化算法的初始點為 (0, 0)。這是算法開始搜索最優解的起點。
配置優化選項:使用optimoptions設置優化過程的選項，Display, iter：在每次迭代時輸出當前狀態，幫助跟蹤優化過程，Algorithm, quasi-newton指定使用擬牛頓法。
使用fminunc函數對目標函數f進行優化，找到其最小值。返回值為最優點min_point和最小值min_value。
為了找到函數的最大值，定義了一個新的目標函數F，該函數是原函數f的負值。通過對負值進行最小化，間接地實現了最大化。再次使用fminunc函數來尋找最大值點和最大值。

三、實驗使用環境

Matlab

四、實驗步驟和調試過程

1、函數求導

1.1求解給定函數的一階導數
代碼如下：

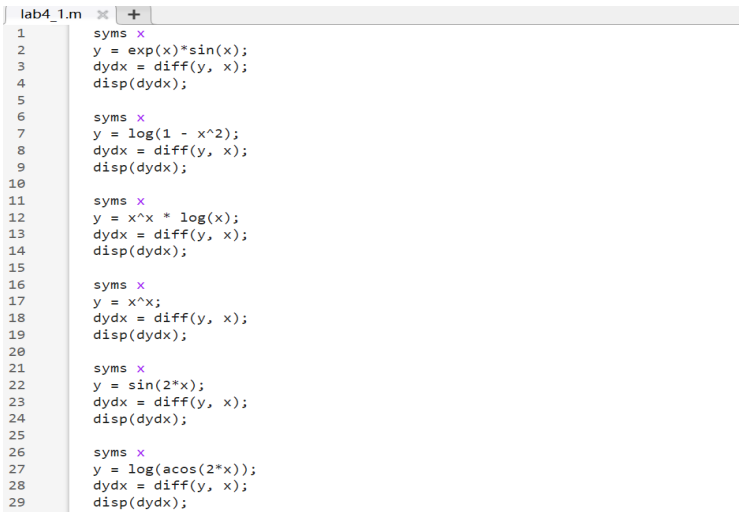
結果如下：

1.2求解給定函數的二階導數
代碼如下：

首先定義符號變量x，接著在求出一階導數的基礎上對其進行再次求導，得出二階導數。
結果如下：

1.3求解隱函數的導數
代碼如下：

使用diff命令對方程兩邊同時取偏導數，得到關于y′的方程，即隱函數的一階導數，再使用simple函數簡化導數的表達式。
結果如下：

2、函數極值

2.1一元函數極值
1）代碼如下：

首先定義符號變量 x，然后定義了一元函數 f。接著計算函數的一階導數，并解出一階導數等于零的所有點，且篩選掉了不在區間 [-5, 1] 內的點。接著計算所有有效極值點的函數值，并從中找到最小的那個。
結果如下：

2）代碼如下：

首先定義平均成本A，即將總成本C除以產量q。然后，求取平均成本A對產量q的導數，以確定平均成本的極小值點。通過解方程導數為零的情況，找出使平均成本最低的產量解。接下來，篩選出所有正的解（因為產量不能為負），并將其轉換為雙精度數值。最后，檢查是否找到了符合條件的解，如果找到了，則輸出該產量及其對應的最低平均成本；如果沒有找到，則輸出相應的提示信息。
結果如下：

2.2多元函數極值
代碼如下：

首先定義目標函數f，并設置一個初始點(0, 0)，為后續的優化算法提供起始位置。接下來，代碼使用optimoptions配置優化選項，選擇無約束優化的fminunc函數，并指定使用準牛頓法來提高收斂速度，同時設置顯示選項為iter，以便在優化過程中輸出迭代信息。再通過調用fminunc，尋找目標函數的最小值，返回最小值點和對應的最小值。為了尋找最大值，通過取負的方式定義了一個新的目標函數F。再次調用fminunc，這次用于尋找這個負函數的最小值，從而間接得到原函數的最大值。最終，輸出最大值點和最大值的結果。結果如下：

五、小結

1、實驗中遇到的問題

問題1：當使用solve()函數時，得到了符號解而不是數字解。
解決：添加了一些額外的檢查以確保只有當在有效的正數解時才輸出結果。并使用double()
函數將符號轉換成雙精度浮點數，以便它可以被num2str()接受。
問題2: 在求解高階導數時，可能會遇到復雜度較高的方程組。
解決: 可以先簡化方程，再逐步求解。

2、實驗中產生的錯誤

錯誤1：梯度計算有誤導致迭代方向錯誤。
原因：可能是數學推導或編碼時出現了疏漏。
錯誤2：程序運行時間過長。
原因：可能是學習率設置不當，導致收斂速度慢。

3、實驗體會和收獲

在本次實驗中，我學習了如何使用Matlab進行復雜的數學分析，掌握MATLAB的符號計算功能，特別是syms, diff, solve等命令的應用；加深了對于導數、極值點、極限等概念的理解，提升了編程技能；了解隱函數求導的方法，學會了如何通過調整參數來改進算法性能；加深了對梯度下降算法的理解。通過這次實驗我提高了解決問題的能力，發現了理論知識與實踐之間的差距，也認識到了理論指導實踐的重要性。