《A Landslide Displacement Prediction Model Based on the ICEEMDAN Method and the TCN–BiLSTM Combined Neural Network》

發表于 Water 期刊，2023年。

---

📌 主要內容概述

這篇論文提出了一種滑坡位移預測模型，結合了：

• ICEEMDAN（改進完全集合經驗模態分解與自適應噪聲法）用于將滑坡累計位移序列分解為：

  • 趨勢項（由滑坡內部地質條件決定）
  • 波動項（由降雨、地下水位等外界因素驅動）

• TCN–BiLSTM 組合神經網絡

  • TCN（時序卷積網絡）提取特征
  • BiLSTM（雙向長短期記憶網絡）捕捉特征間的時序關系
  • 結合兩者，提升對滑坡位移波動項預測的精度，尤其是復雜非線性時序數據。

---

📌 核心方法流程

1. 數據分解：

   • 用 ICEEMDAN 將滑坡位移數據分解成多個 IMF 和殘差項。
   • 殘差項作為趨勢項，其余 IMF 疊加成波動項。

2. 趨勢項預測：

   • 采用三次多項式擬合，預測趨勢項未來走勢。

3. 波動項預測：

   • 通過灰色關聯度（GRG）和最大信息系數（MIC）篩選主要影響因子：

     • 前幾天的位移、降雨量、地下水位及其變化

   • 使用 TCN 提取高維特征，輸入 BiLSTM 網絡進行時序預測。

4. 預測值重構：

   • 將趨勢項和波動項預測值相加，得到總位移預測值。

5. 效果驗證：

   • 對比了 LSTM、BiLSTM、TCN、TCN–LSTM 和 TCN–BiLSTM 等5個模型，結果顯示：

     • TCN–BiLSTM 綜合性能最佳，MAPE 僅 0.002，R2 高達 0.999。

---

📌 應用案例

• 研究對象：四川通江縣萬家灣滑坡

• 監測內容：

  • 地表位移、降雨、地下水位（65個時段）
  • 發現降雨和地下水位是主要觸發因素，滑坡位移存在顯著滯后性。

---

📌 結論

• ICEEMDAN 分解方法 能有效提高數據物理意義和預測準確性。
• TCN–BiLSTM 組合模型 在處理滑坡非線性波動位移預測時表現優異，適合用于滑坡預警、工程建設安全管理。
• 后續建議：關注模型復雜度和計算資源消耗，合理篩選輸入特征以優化效率。

---

全文翻譯

摘要
受原生地質條件和外部環境變化的影響，滑坡演化多為非線性演化。針對傳統遞歸神經網絡在位移波動型滑坡預測中的不足，提出了一種結合時間卷積神經網絡(TCN)和雙向長短期記憶神經網絡(BiLSTM)的組合神經網絡預測模型。基于時間序列分解的思想，采用改進的帶自適應噪聲的全系綜經驗模態分解(ICEEMDAN)方法，將位移時間序列數據分解為趨勢項和波動項。趨勢位移主要受滑坡內部地質條件的影響，采用多項式擬合確定未來趨勢位移;波動項的位移主要受滑坡外部環境的影響。本文選取降雨、地下水位高程、滑坡歷史位移三種類型的滑坡影響因素。它使用灰色關聯(GRG)和互信息(MIC)關聯模塊的組合進行特征篩選。然后利用TCN提取滑坡特征因子，BiLSTM捕捉特征與位移之間的關系，實現對波項位移的預測。最后，對趨勢項和波動項位移預測值進行重構，得到總位移預測值。結果表明，本文提出的ICEEMDAN-TCN-BiLSTM模型能夠準確預測滑坡位移，具有較高的工程應用價值，有助于滑坡防災工程的規劃和建設。

關鍵詞* 滑坡位移預測;時間分解;神經網絡;地質災害

1. 簡介

山體滑坡作為世界上發生最頻繁、分布最廣泛、破壞性最強的地質災害之一，對附近居民的安全、生命和財產造成了重大影響[1-5]。據統計，每年山體滑坡造成4500人死亡，每年山體滑坡造成的經濟損失可高達200億美元[6]。可引發滑坡的因素包括降雨[7-12]、地下水位變化[13-16]、地震[17-19]、人類工程活動[20,21]等，這些因素都有可能引發滑坡等地質災害。因此，分析和考慮滑坡的影響因素，建立高精度的滑坡位移預測模型，對于準確把握滑坡演化階段，減少滑坡災害損失具有重要意義[22,23]。

滑坡累積位移由隨時間變化的趨勢項位移和由外部因素[24]引起的位移波動項組成。將滑坡累積位移分解為具有實際物理意義的分量，分別建立預測模型，可有效預測滑坡的累積位移。Du et al.[25]將滑坡累積位移分解為趨勢項和波動項，并使用BP神經網絡預測位移分量。Yang等人[26]使用移動平均法分離滑坡累積位移，并使用支持向量機(SVM)預測周期項位移。Liu et al.[27]使用聚類分析(K-means)表征了滑坡的外部位移和內部狀態，并使用支持向量機(SVM)和長短期記憶神經網絡(LSTM)預測了滑坡位移。Zhang等人[28]采用變分模態分解(VMD)將監測值分解為高頻、中頻和低頻分量，并構建深度雙向長短期記憶神經網絡(BiLSTM)分別預測位移分量。Zhang等人[29]采用完整集合經驗模態分解(complete ensemble empirical mode decomposition, CEEMD)對累積位移觀測值進行分解，并通過多群智能算法(multi-swarm intelligence algorithms, MSI)對SVR模型進行優化，實現滑坡位移預測。

上述方法都取得了不錯的效果，但也有各自的不足。在位移時間序列分解方面，移動平均法操作簡單，但只能提取位移的趨勢項，無法獲得滑坡位移的波動項部分。K-means方法對時間序列數據進行分解重構，重構后的數據不具有實際的物理意義。VMD方法可以自由選擇位移分量的個數，但對初始條件的依賴性高，計算復雜。CEEMD方法在分解時間數據時存在模態混疊和殘留白噪聲的問題[30,31]。針對這些問題，ICEEMDAN[32]方法減少了偽模態的數量和殘余白噪聲的影響。與CEEMD方法相比，該方法還具有較小重構誤差少、計算收斂速度快等優點，被廣泛應用于生物醫學工程和計算機科學等領域[0]。因此，本文采用ICEEMDAN方法對滑坡位移進行分解，提高數據分解質量，使分解項更具物理意義。

預測滑坡位移依賴于預測模型的發展。目前使用的預測模型主要可分為靜態模型和動態模型[34-36]。常用的靜態模型包括支持向量機回歸模型(SVR)和極限學習機模型(ELM)。由于山體滑坡的位移行為主要由外部條件的變化引起，靜態模型往往難以考慮山體滑坡復雜的演化過程，無法有效提取歷史序列數據[37]。動態模型考慮了時間序列數據的歷史特征，如Yang等人[38]和Zhang等人[39]使用LSTM神經網絡預測滑坡周期項的位移，其預測效果優于靜態模型SVM。Zhang等[40,41]利用門控循環單元(gated recurrent unit, GRU)動態模型挖掘時間數據中的有效歷史特征，實現了滑坡位移波動段的準確預測。傳統的動態模型雖然已經實現了滑坡時間位移的動態預測，但由于滑坡災害的突發性和破壞性以及監測樣本數據的局限性，其預測精度受到限制。LSTM神經網絡需要大量的訓練數據，這會導致計算成本增加，模型泛化能力差。然而，GRU神經網絡的計算效率優于LSTM神經網絡，但其簡化的門控結構不能更好地保留和傳輸信息。Lin等[36]采用雙向長短期記憶神經網絡(bidirectional long - short memory neural network, BiLSTM)同時考慮影響滑坡位移的歷史和未來因素，有效預測了白水河滑坡的位移。由于其獨特的雙向處理結構，BiLSTM神經網絡通常可以提供更豐富的特征表示，這意味著它可以學習與傳統的LSTM和GRU相比，預測精度得到了進一步提高。

近年來，時間卷積網絡(temporal convolutional network, TCN)神經網絡在氣象數據預測、計算機數據挖掘等領域得到了廣泛的應用。例如，P. Hewage等人將TCN應用于氣象預報，實現了對未來天氣的長期預測。Fan等人[43]提出了一種基于TCN神經網絡的PSTA-TCN框架，通過并行計算顯著縮短了模型的訓練時間，同時顯著提高了準確率。TCN具有擴展的因果卷積結構和出色的特征提取能力，可以挖掘多維特征時間信息。目前，BiLSTM-TCN組合模型很少用于各種社區，幾乎從未應用于滑坡災害。滑坡災害由于其突發性和季節性，往往表現出非線性位移曲線。預測模型的特征提取和學習能力對于準確預測滑坡位移至關重要。

本文將BiLSTM與TCN相結合，應用于非線性時間位移的預測。通過TCN提取特征變量，并將其輸入到時間序列網絡BiLSTM中，大大提高了時間序列網絡中記憶單元的處理效率，從而減少了訓練時間，獲得了更準確的預測結果。

本文以萬家灣滑坡為研究區域。采用ICEEMDAN分解方法，將滑坡位移監測值分解為具有實際物理意義的趨勢項和波動項。擬合多項式得到趨勢項位移預測公式，用于預測趨勢項位移。采用GRG灰色關聯和MIC互信息值的雙指標篩選方法，對位移分量、降雨量和地下水位三個候選影響因素進行篩選，得到相關性最大的影響因素。然后，將選取的影響因素作為BiLSTM-TCN組合模型的輸入，對模型進行超參數優化訓練，用于滑坡波動位移預測。最后，將趨勢項的預測位移與波動項的預測位移疊加，得到滑坡的累積位移預測值，并對其進行驗證和分析。滑坡位移預測流程圖如圖1所示。

圖1 滑坡位移預測流程圖:(a)數據處理，(b)位移預測，(c）模型驗證。

2. 方法

2.1. 經驗模態分解

EMD在信號處理、振動分析等領域有著廣泛的應用。其本質是將非平穩信號數據分解成一系列具有不同特征尺度的序列。分解后的序列稱為內稟模態函數(IMF)， IMF的不同內稟模態分量表示不同的特征波動序列。具體分解過程如下[44,45]。

1. 標記監測數據x(t)中的極值點，并將局部最大值點和局部最小值點分別連接起來，形成上下包絡曲線，其中m1(t)為上下包絡線之間的均值曲線。

2. 進行第一次篩選，第一分量C1(t)的計算公式如下:

在第二次篩選過程中，C1(t)被認為是原始數據，m2(t)是上下包絡線之間的平均曲線。重復上述步驟，即可得到分量C2(t)。

3. 重復上述篩選過程，直到Cn(t)為內稟模態函數或殘差分量rn(t)變為單調函數，分解過程終止。

4. 分解后的IMF項與rn(t)項之和即為原序列，x(t)公式如下:
   

2.2. 改進的全系綜經驗模態分解與自適應噪聲

CEEMDAN通過加入高斯白噪聲解決了EEMD模式混疊和殘余噪聲問題。ICEEMDAN與CEEMDAN不同，后者在分解過程中直接加入高斯白噪聲。而是選取EMD分解后的白噪聲的第k個IMF分量，即噪聲Ek(ω(i))。以下是ICEEMDAN[30]的一般步驟。

1. 將噪聲E1(ω(i))加到原始信號x上，得到:

式中，β0為噪聲標準差;ω(i)為加高斯白噪聲。

2. 計算第一個模態分量的IMF值:

式中，r1表示一階殘差;c ~ 1為第一模態分量IMF值。

3. 計算第二個模態分量的IMF值:

式中，r2表示二階殘差;c ~ 2為第二模態分量IMF值。

4. 以此類推，計算第k個模態分量的IMF值:

式中，rk表示k階殘差;c ~ k是第k個模態分量的IMF值。

2.3. Temporal Convolutional Network

TCN是一種卷積神經網絡，旨在解決遞歸神經網絡中的常見缺陷。它通常用于挖掘圖像信息和預測序列數據。TCN結構比典型遞歸網絡更簡單清晰，主要由因果卷積核和殘差模塊[46]組成。

2.3.1. Causal Dilated Convolutional

因果卷積可以理解為時間數據的單向傳輸。與傳統的卷積神經網絡不同，在因果卷積中，未來的數據不能影響過去，只在當前和之前的時間步長執行卷積操作。因此，它被稱為因果卷積[47]。

如圖2所示，在基于因果卷積的卷積過程中，允許對輸入進行區間采樣。如果d = 1，則表示對每個數據點進行采樣;如果d = 2，則表示每兩個數據點采樣一次。類似地，卷積網絡可以得到

即使在更少的卷積層中，也能獲得更大的接受場。式(7)是因果擴張卷積[43]的數學表達式:

**圖2。**因果展開卷積結構圖。

式中，yh,t表示時間t時網絡中h層的序列值，fi表示濾波器，k表示卷積核的大小，d表示卷積展開率。

2.3.2. 殘差塊

殘差模塊是訓練深度網絡的一種有價值的技術，因為它允許在層之間發送信息，這有助于防止深度網絡訓練期間梯度消失或破裂[48,49]。如圖3所示，本文構建了一個殘差塊來代替卷積層。兩層非線性映射和卷積構成了一個殘差塊。

**圖3。**殘塊結構圖。

2.4. BiLSTM

LSTM是一種改進的遞歸神經網絡，它引入了一種稱為“門”的內部機制，通過學習重要信息和遺忘次要信息來調節信息流，從而更好地處理序列中的長期依賴關系。與標準LSTM不同，BiLSTM同時運行兩個獨立的LSTM網絡，一個處理前端輸入序列，另一個處理后端輸入序列，如圖4所示。這使得網絡能夠捕獲每個時間步之前和之后的信息，包括過去和未來的信息。

2.5. TCN-BiLSTM

由于采用了擴展的因果卷積結構，TCN具有出色的特征提取能力。因此，TCN可以融合原始特征獲得更高維度的抽象特征，從而加強對特征信息的挖掘。BiLSTM網絡具有較強的時間預測能力。通過結合TCN和BiLSTM網絡，

將TCN特征提取并輸入到BiLSTM網絡中，提高了BiLSTM網絡記憶單元的計算性能，使預測模型更有效地學習時間序列的復雜交互關系。因此，本文構建了TCN-BiLSTM預測模型，組合模型結構如圖5所示。

**圖4。**BiLSTM神經網絡結構圖。

**圖5。**TCN-BiLSTM組合模型結構圖。

2.6. 評價指標

本文選取滑坡位移預測中常用的均方根誤差(root mean square error, RMSE)、決定系數(coefficient of determination, R2)和平均絕對百分比誤差(mean absolute percentage error, MAPE)等技術，對模型的準確性和適用性進行評價。以下是測量指標的計算公式:

公式中，yk為第k個真值樣本，yk為第k個預測值樣本，yk為所有真值的算術平均值。根據RMSE、MAPE、R2的計算結果進行評價，三者的計算結果均在0 ~ 1的范圍內。

3. 研究區概覽

3.1. 概述

萬家灣滑坡位于四川省通江縣北部興隆鎮安平村。它位于通江縣北部，大同江西側，小同江東側。地形起伏較大，總體呈東北高、西南低的趨勢。坡度方向228?左右，地形坡度一般為10-20?。滑坡后緣左側與工程場地平整區相鄰，滑坡坡腳位于生活營地內，如圖6所示。

**圖6。**萬家灣滑坡:(a)滑坡邊界及監測點布置圖;(b) II-II段地質剖面圖。

滑坡整體高程在840 ~ 890 m之間，整個滑坡區寬度約222 m。整體平面形狀呈“圓椅”狀。滑坡縱向長度約為275 m，面積約為3.84 ×104 m2。含碎石的粉質粘土構成了滑坡體的大部分，礫石則主要由砂巖塊組成。滑坡體積在38.4 ×104 m3左右，滑坡體平均厚度在10 m左右。滑動帶為軟塑性粉砂質粘土期含少量角礫巖，透水性差，可形成相對不透水層。滑層為下伏基巖，主要由強至中度風化的碳質砂質泥巖和砂巖組成。

3.2. 宏觀變形特征

萬家灣滑坡屬淺層滑坡，規模為中型滑坡。由于地表土層暴露，加之長期降雨的綜合作用，最終發生了滑坡災害。2022年7月7日，井臺北側上層居住區出現裂縫(圖7a)，裂縫最大寬度為20 mm，裂縫最大長度為500 mm。2022年7月19 - 27日在坡腳區進行開挖施工，期間發生兩次降雨事件。現場現有裂縫擴大，后緣工程現場平坦區域出現新的裂縫(圖7b)。從2022年8月7日開始，在滑坡區設置位移監測點和地下水位監測點。監測期間，既有裂縫不斷加劇，新的裂縫不斷出現(圖7c)。2022年8月7日至28日，除滑坡中心找平區外，位移和變形相對穩定，整體變化較小，而充填區變形較大。2022年8月30-31日連續兩天降雨后，發生在居民區的地表沉降裂縫整體變形(圖7d)明顯加劇。綜合分析，滑坡已處于蠕變變形階段，雨后有加劇的趨勢。

圖7。滑坡裂縫發育照片:(a)滑坡后緣裂縫，(b)工程場地平坦區域裂縫，?滑坡中部裂縫，(d)臺階裂縫。

3.3. 監測數據及觸發因素分析

影響滑坡的因素往往非常復雜，根據其來源可分為內部因素和外部因素[50-52]。不利的環境地質條件，包括斜坡地貌、厚而松散的土層、高度風化的巖性、工程開挖形成的大規模自由面等，是滑坡[53]發生發展的主要內部因素。在內部因素的影響下，滑坡的時間位移關系曲線呈現近似單調函數，反映了滑坡整體累積位移的趨勢項。外部因素不同于靜態因素，主要是滑坡外部的動態環境因素，包括自然降雨、地下水位、風荷載、環境溫濕度等。在外界因素的影響下，滑坡的時間位移關系曲線呈現出一定的波動規律。

本工程采用多種監測方法，獲得的監測數據主要包括降雨量、地下水位、地表位移、深部土體位移等。以上數據均來源于現場工程監測報告。對各監測點的數據進行處理分析后，位于滑坡中下部的地表位移監測點D1、D18、J12在整個監測周期內均呈現明顯的位移發展趨勢。選取上述3個地表位移監測數據和位于滑坡中段的地下水位監測點數據進行研究。所有監測數據包括65個時間段(從2022年8月7日到2022年10月10日)，如圖8所示。

圖8。萬家灣滑坡累積位移、降雨量、地下水位監測資料。

監測期為夏季降雨頻繁期，地下水位波動頻繁。8月初和8月底發生了兩次暴雨事件，導致地下水位急劇上升，期間各監測點的累計位移明顯增加。非降雨期，地下水位呈緩慢下降趨勢，累計位移增速放緩。8月份的兩次暴雨打破了萬家灣邊坡原有的穩定狀態，邊坡的整體安全儲備大大減少。9、10月連續降雨下，累積位移增長趨勢變大，且地下水位上升后累積位移明顯增大。在監測周期內，幾乎所有的位移加速階段都發生在降雨事件之后和地下水位波動期間，說明地下水位與降雨量的變化具有一定的

對滑坡變形影響顯著。在降雨的作用下，雨水沿著地表裂縫向下滲透到相對不透水的滑動帶界面，底部的軟質、塑性、粉狀粘土被浸透軟化，導致滑動帶的物理機械強度不斷下降。同時，隨著土壤含水率的增加，滑動體的重力也隨之增大。當滑動力超過抗滑動力時，土壤就會發生滑動。因此，滑坡位移的加速階段往往發生在降雨事件之后。隨著降雨事件的持續，地下水得到大氣降雨的補充，導致水位急劇上升。邊坡內部的應力場和滲流場在短時間內發生顯著變化，從而加速滑坡事件的發生。因此，地下水位的波動也會導致滑坡的加速發生。

4. 結果

4.1. 數據分解

通過對所有監測數據的處理和分析，位于滑坡中心區域的D1監測點數據呈現出明顯的位移趨勢。由于此時監測數據的完整性較好，因此本文利用該位移序列建立了萬家灣滑坡預測模型。我們選取了2022年8月7日至2022年9月27日的52個監測數據集作為訓練樣本。測試樣本為以下13個數據集，時間為2022年9月28日至2022年10月10日。本工作在MATLAB 2022a環境下開發了ICEEMDAN算法，并利用該算法對所選位移序列樣本進行解構，如式(3)-(6)所示。該過程的參數設置如下:200次迭代為最大值，標準差比為0.15。

分解后的數據如圖9所示。將原始位移序列樣本劃分為4組位移序列分量，其中IMF1分量波動頻率最高，其次是IMF2和IMF3分量，剩余分量R相對平穩，幾乎沒有波動。因此，殘差分量R作為趨勢項位移，波動顯著的分量IMF1-IMF3之和作為波動項位移。合并后的數據如圖10所示。

圖9。滑坡總位移ICEEMDAN分解項:(a) IMF1， (b) IMF2， ? IMF3， (d) R。

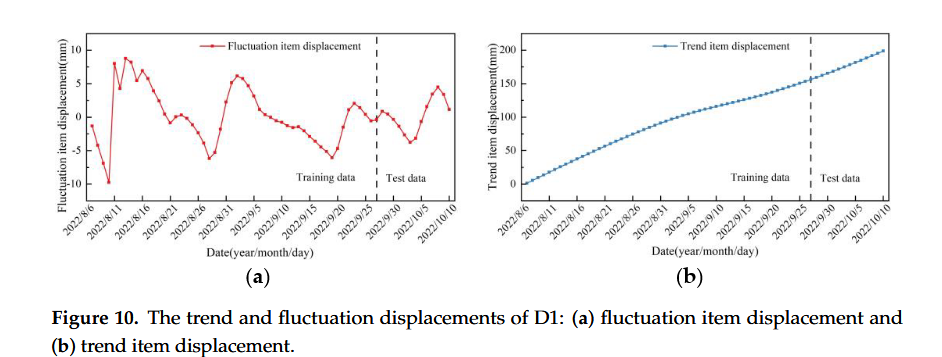
圖10。D1的趨勢和波動位移:(a)波動項位移和(b)趨勢項位移。

4.2. 確定影響因素

影響因素的合理選擇決定了預測模型準確率的上限[54-56]。Du等人[57]的研究表明，滑坡過去的狀態可以在一定程度上影響滑坡的發展趨勢。因此，本文將位移監測值作為滑坡的影響因素之一。在研究河岸邊坡時，降雨和水庫水位往往被認為是影響滑坡位移的主要因素[58,59]。本文的研究區域位于大同河與曉通河之間，滑坡區離河面較遠。因此，未考慮水庫水位對滑坡的影響。根據現有的工程監測資料并仔細考慮，降雨、地下水位和歷史位移是萬家灣滑坡的主要影響因素。

圖11為地下水位、日降雨量與波動項位移之間的關系。從圖中可以觀察到，在降雨頻繁的時期，滑坡區內波動項的位移變化明顯。在無小雨或有小雨的天氣環境中，波動項的位移變化相對平穩。考慮到歷史降雨對滑坡未來狀態的影響較大，本文將當日、前一日、兩天的累積降雨量作為影響滑坡位移的關鍵因素(輸入4-6)。進一步，滑坡區地下水位變化與降雨量之間存在正相關關系，且波動項的位移在地下水位上升時呈現快速增大的趨勢。當地下水位略有變化或保持在一定范圍內時，波動項的位移變化較小。且波動項的位移往往發生在地下水位上升之后，且地下水位變化對波動項位移的影響具有滯后效應。因此，本文將當日地下水位高程值、前一日及后地下水位變化、與前一日相比地下水位變化減少(輸入7-10)作為波動項位移的關鍵影響因素。最后，本文以前一天的位移、前兩天的位移和前一天的累計位移作為波動項位移的影響參數(輸入1-3)。

根據上述分析結果，本文初步選取了10個可能的候選因素，如表1所示。圖12顯示了各因素之間的GRG和MIC值。灰色關聯度分析結果表明，降雨和地下水位對波動項位移的影響較大。相比之下，歷史位移因子對波動項位移的影響相對較小。最大信息系數分析結果表明，過去一天的位移、每日地下水位高程、與前一天相比地下水位變化減少量與波動項的位移相關性較低。另一個候選項因子項與波動項的位移有較好的相關性;其中，前一天累計位移與波動項位移高度相關。為保證預測結果的準確性，本文選取滿足GRG值大于0.80、MIC值大于0.25條件的候選因子作為預測模型的主要影響因子。因此，本文排除了輸入1、輸入7和輸入10三個候選因素，并將其余7個因素確定為影響滑坡波動項位移的關鍵因素。

圖11。地下水位、日降雨量與波動項位移變化的關系。

表1。候選因素。

圖12。影響因素的相關分析:(a) GRG和(b) MIC。

4.3. 位移預測

4.3.1. 趨勢項目位移預測

趨勢項位移使用多項式回歸方程進行擬合。為了盡可能保證數據的預測精度，避免使用高階多項式進行過擬合，本文進行了多次實驗分析，最終確定使用三次多項式對數據進行擬合。擬合公式如下，擬合優度R2為0.999，說明擬合效果極佳。

式中，y表示趨勢項的位移，x表示時間。

上述方程作為預測模型中趨勢項的預測公式，圖13顯示了趨勢項的位移預測結果。MAPE為0.002,RMSE為0.425,R2為0.999。評價指標的計算結果表明，采用三次多項式擬合方法進行趨勢位移預測可以取得較好的預測效果。

圖13。趨勢項目位移預測結果。

4.3.2. 波動項位移預測

在TCN模型中，擴展因子設為4，卷積核大小設為3，隱藏層數設為4。LSTM和BiLSTM模型的隱層神經元取64個。在訓練過程中，輸入特征是經過相關濾波后最相關的7個特征，將前5組歷史數據作為模型預測未來兩組數據的輸入項。該模型采用貝葉斯優化算法進行超參數優化。組合模型也遵循單個模型的參數設置。

圖14顯示了不同神經網絡的預測結果。LSTM神經網絡對波動項位移的預測效果最差，TCN神經網絡次之，BiLSTM神經網絡次之。根據預測結果計算的預測誤差如表2所示。具體分析如下:

1. 由于工程項目提供的滑坡監測數據有限，訓練后的LSTM模型泛化性能較差，導致R2為0.915，預測性能不理想。

2. 由于其獨特的雙向處理結構，BiLSTM神經網絡通常提供更豐富的特征表示，這意味著它們可以更好地捕獲輸入序列中的模式和關系。從總體誤差分布來看，BiLSTM的預測誤差略低于LSTM的預測誤差。最終計算結果LSTM神經網絡的預測結果R2為0.945，預測效果優于LSTM。

3. 由卷積神經網絡進化而來的TCN比LSTM需要更少的參數，使其更容易訓練和調整。因此，即使在有限的訓練數據支持下，TCN神經網絡也可以實現更準確的位移預測。最終TCN神經網絡R2計算結果為0.945，預測效果優于LSTM。

圖14。不同神經單網絡波動項的位移預測結果。

表2。不同神經網絡模型的預測誤差。

總體而言，上述三種類型的神經網絡在波動項位移曲線的單調增減階段都取得了較好的預測性能。但在波動項位移曲線的拐點處仍會存在明顯的誤差，無法達到準確預測的目的。

單個神經網絡組合預測波動項位移的情況如圖15所示。從整體預測誤差來看，組合的兩個神經網絡模型改善了波動項位移曲線拐點處預測不準確的問題，模型的整體預測精度更高。其中，TCN-BiLSTM的預測性能優于TCN-LSTM。具體分析如下。

TCN具有因果擴展卷積結構和出色的特征提取能力。它可以融合原始特征，獲得高維抽象特征，增強特征信息的挖掘。LSTM和BiLSTM時間序列網絡具有較強的時間預測能力，可以更好地捕捉輸入序列中的模式和關系。lstm型網絡可以與TCN網絡結合進行波動項位移預測。通過TCN提取特征變量并將其輸入到時間序列網絡中，大大提高了時間序列網絡中存儲單元的處理效率。因此，組合預測模型在學習時間序列的復雜交互關系方面更加有效。

圖15。帶波動項的不同組合神經網絡的位移預測結果。

從絕對誤差分布直方圖上看，TCN-BiLSTM的總體誤差分布小于TCN-LSTM。通過計算，得到了利用兩種組合網絡進行滑坡波動項位移預測的預測誤差指標。與TCN - lstm相比，TCN與BiLSTM的組合使MAPE平均降低了71.955%，使得TCN - BiLSTM組合網絡的預測精度更高。

4.3.3. 總位移預測

如圖16所示，將多項式擬合預測的趨勢位移與TCN-BiLSTM聯合神經網絡預測的波動位移疊加，得到滑坡的總預測位移。通過將滑坡總預測位移與實際值進行對比，發現預測的滑坡總累積位移與實際值高度吻合。總預測位移中，MAPE為0.002,RMSE為0.406,R2為0.999，預測效果較好。

圖16。滑坡總位移預測結果。

實驗結果表明，該模型對滑坡起伏項位移的預測精度高于其他5種模型。對于非線性波動項位移曲線，曲線拐點處數據點的準確預測至關重要。模型的特征提取和學習能力決定了位移預測的準確性。與LSTM相比，TCN和BiLSTM在單個神經網絡中的預測誤差更小。這是由于TCN模型具有出色的特征提取能力，可以深入挖掘非線性特征。雙向LSTM網絡結構可以充分利用輸入特征信息，獲得更豐富的特征表示進行學習。將TCN與BiLSTM相結合可以實現對非線性特征的準確預測。萬家灣滑坡波動項的位移與降雨和地下水位高度有關，這些特征變化在雨季往往是非線性的。因此，構建TCN-BiLSTM組合模型可以更準確地把握滑坡的運動趨勢。

另一方面，TCN-BiLSTM組合模型具有較高的復雜度，需要更多的計算資源和訓練時間。因此，在訓練過程中選擇關鍵的輸入特征就顯得尤為重要。

5. 結論

本文重點研究了降雨誘發滑坡的高精度位移預測問題，深入分析了影響因素與滑坡累積位移的關系，并結合BiLSTM和TCN的優點，提出了基于TCN - BiLSTM聯合結構神經網絡的降雨誘發滑坡位移預測模型。并將該預測模型應用于萬家灣滑坡的位移預測，并將其預測結果與LSTM、TCN、BiLSTM和TCN - LSTM模型的預測結果進行了比較。得到以下結論:

(1) ICEEMDAN算法對滑坡位移-位移序列分解具有較強的適應性。通過選擇合理的信噪比分解，可以將滑坡累積位移有效分解為相對穩定的高頻波動項和低頻殘差項，得到的位移分量具有實際物理意義。

(2)在預測滑坡位移波動項的特征數據選擇中，降水、地下水位、滑坡歷史位移與滑坡波動項的位移分量高度相關。本文采用GRG-MCI組合篩選方法對處理后的參數數據進行處理，識別出的影響因素與滑坡波動項的位移分量高度相關。

(3)對于滑坡趨勢位移預測，采用多項式擬合方法可獲得較好的預測結果，預測值R2為0.999，表明預測精度較高，能較準確地反映滑坡位移的趨勢變化。在預測滑坡波動項位移時，TCN - BiLSTM組合結構神經網絡模型能準確捕捉滑坡位移的波動變化，預測值R2為0.997，優于傳統的LSTM、TCN、BiLSTM和TCN - LSTM模型。

(4)本文采用ICEEMDAN-TCN-BiLSTM模型對萬家灣滑坡D1監測點位移進行預測。對預測結果的各項評價指標證明，該模型對滑坡位移預測具有較高的適用性。據此推斷，該方法可有效應用于其他滑坡位置的位移預測。但其在預測其他類型滑坡位移方面的適用性仍需進一步驗證。