在這里，我們來看一下（Arikan，2009）中提供的連續取消解碼算法。

顧名思義，SC解碼算法從u0開始按順序解碼比特。

• 凍結的比特節點總是被解碼為0。

在解碼ui時，根據以下規則使用由向量表示的可用比特來解碼ui：

其中A是信息位置的集合。

概率計算在計算上更容易，在對數域中不太容易出現舍入誤差。

• 因此，我們考慮LLR而不是概率來避免數值溢出。

第t位的LLR定義為：

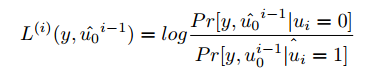
因此，決策規則更改如下：?

極性碼的二叉樹結構可以用來簡化連續抵消解碼。

????????二叉樹有個階段，編號從s=0開始到n，即。每個階段s包含節點，每個節點對應位。

依次遍歷樹以執行連續的抵消解碼。

• 在每個節點上，消息傳遞如下：每個節點將LLR對應的LLR值（即α）傳遞給子節點，并在sage（即β）處向父節點發送估計的硬比特。左消息和右消息計算如下：

?

?我們定義了兩個函數來執行這些操作，即f和g，定義如下：

?但是f函數的計算成本很高，因此，我們使用最小和近似法將其近似為硬件友好版本，如下所示：

其中sign表示輸入的符號，min表示兩個輸入中的最小值。

該算法從樹的根節點（級別n+1）開始，遍歷到葉節點（級別0）。

對于每個節點，都會發生以下一組操作。

1. 如果當前節點有一個未被訪問的左子節點，則計算αl并移動到左子節點。
2. 如果當前節點有一個未被訪問的右子節點，則計算αr并移動到右子節點。
3. 如果來自子節點的兩條消息都可用，則計算β并移動到父節點。

一旦到達葉節點，就使用二進制量化函數h基于相應LLR的符號做出決定，如下所示：

?

?

?

?

?