閆式dp分析法:
從集合角度來分析DP問題。
核心思想:
DP是一種求有限集中的最值或者個數問題
由于集合中元素的數量都是指數級別的,直接用定義去求,把每種方案都用dfs暴力枚舉一遍,時間復雜度很高,此時用DP問題去優化。
DP 優化兩個階段(核心思想)

?動態規劃解題步驟
步驟一:確定集合以及集合的屬性
將問題看成一個集合,按照上述集合劃分依據,分成若干不同子集。
按照屬性定義狀態,例如用 f[i] 表示考慮前 i 個元素時的某種最優解或狀態。
?步驟二: 狀態計算
找出狀態之間的關系,即狀態轉移方程。這個方程描述了如何從已知子集的解構建出整個集合的解。?
步驟三:確定初始值
確定基本情況或邊界條件。這些是狀態轉移方程中無法通過遞推得到,需要直接給出的值。有時候可以直接將f數組定義為全局數組,則數組的元素會被默認初始化為0。?
例如f[0] = 0 ,表示容量為0時的最大價值為0。?
步驟四:輸出結果
根據問題的要求,輸出最終結果。在很多情況下,最終結果存儲在 f[n] 中,其中 n 是問題的規模。?
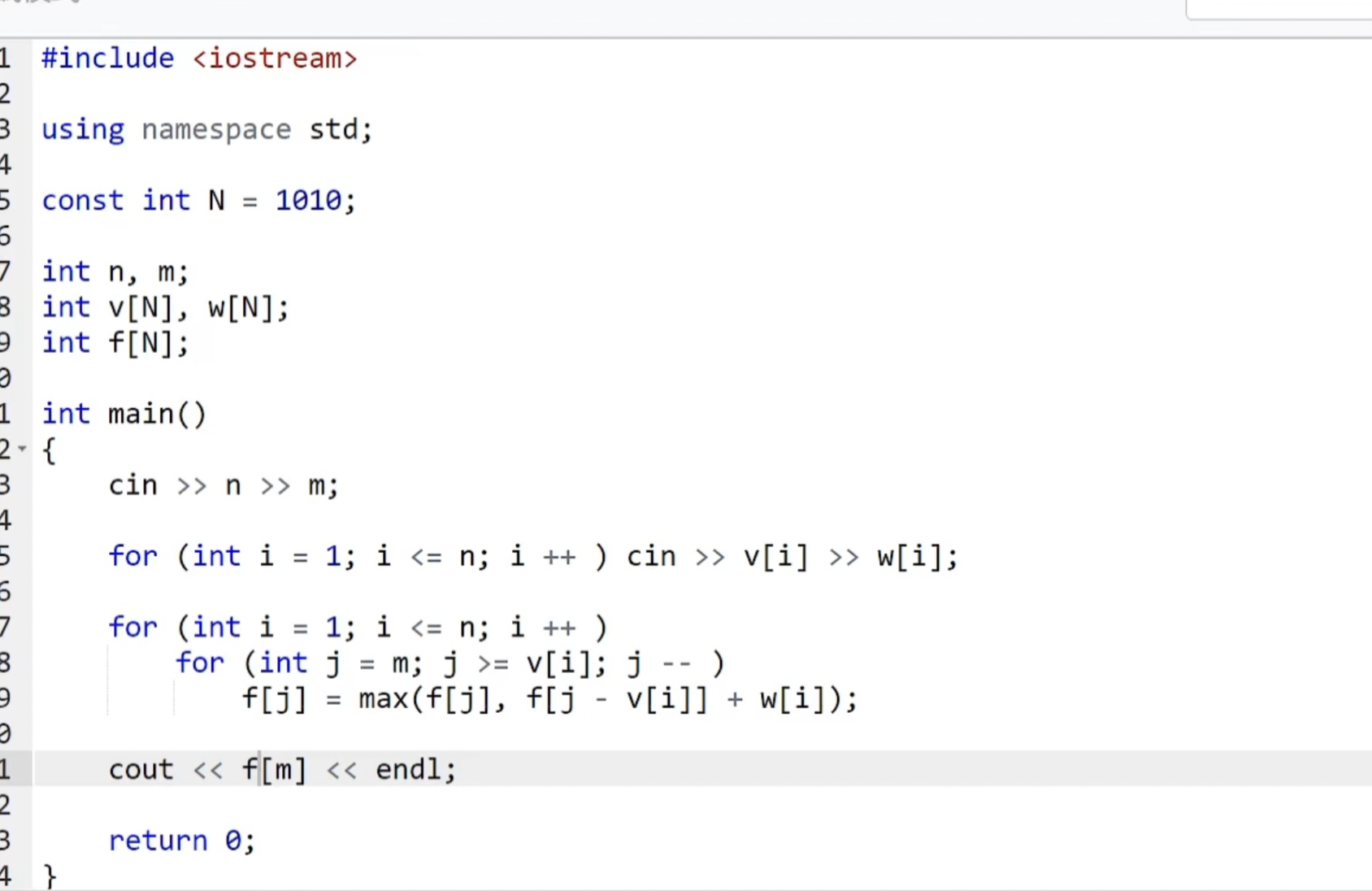
eg:01背包問題
分析:
從2的n次方個方案中,找到總價值最大的方案,即有限集合中的最值問題,用閆式DP分析法來做。

分別求出左邊的最大值,右邊集合的最大值,兩邊取max,就是f(i,j)?的值

左邊=f(i-1,j)
右邊:每個方案都包含i,不變,要想值最大,需要前面變化的(1~i-1)部分最大
樸素代碼

?優化空間后的代碼
DP問題所有的優化都是對代碼做等價變形
等價變形過程如下

?由上圖分析可得,與原方程不等價。為了使之等價,可以將內層倒序循環(由大到小循環),這樣fj會比這件f(j-vi)先更新,那么此時用到的j-vi一定是上一層的,即第i-1層。

繼續優化,刪掉恒等式f[j]=f[j]等得到優化結果
注意:
必須保證代碼優化后是等價的?
內層循環:遍歷每個可能的容量是為了計算在不同容量限制下的最大價值,確保我們考慮了所有可能的容量。因為在考慮第i個物品是否放入背包的時候,我們需要用當前背包的容量減去第i個物品的體積,而第i個物品的體積是任意的,因此我們需要考慮第i個物品在所有可能的容量限制下的最大價值,從而能夠通過比較放入和不放入當前物品時的價值計算出在每個容量下的最大價值。
eg2:完全背包
閆式DP分析問題

?樸素代碼

優化空間后的代碼
按照01背包問題的方法做等價變形過程如下

?如圖,恰好等價
繼續優化,刪掉恒等式f[j]=f[j],將判斷條件放到內層循環初始化里,因為不滿足這個條件的部分會被直接跳過。
得到代碼

兩個問題狀態轉移方程如下

eg3:石子合并(區間DP問題)
分析

第一次可以選擇合并的堆數是n-1,因為一共有n排,選擇的相鄰堆一共n-1種選法。第二次合并的時候,就剩下n-1堆,相鄰兩堆的個數只剩下了n-2,所以第二次合并的時候只剩下了n-2種選法,以此類推,所有不同的合并順序一共有(n-1)!種。
滿足有限集,方案很多,可以考慮DP
由分析可知,最后合并的時候一定是把左邊的某一段和右邊的某一段合并,因此可以分界點作為劃分的依據,具體來說可以以左半邊連續一段的最后一堆,如上圖,最后一堆可以在第i個位置,以此類推。但至少要有兩堆,所以左邊這一堆最大到j-1,因此可以分成上面的j-i類。
現在只要把每一類求出來取一個min,即每個子集的min,再從這些min中取出一個最小值,就是整個集合的最小值。
最終的f[i][j]枚舉k,從i到j-1 ,在里面取一個min即可。
代碼

區間dp問題:先枚舉區間長度,再枚舉區間左端點,若區間長度為1,不用合并,所以從長度2開始枚舉。
因為要在區間長度一定的情況下,在同一[i,j]區間枚舉所有k的可能取值中最f[i][j]的最小值,可以先讓f[i][j]等于一個正無窮,然后再枚舉k
f[i][j]含義:所有將[i,j]區間合并成一堆的方案的集合中的最小值。
總體思想:把這一排石子看成一個集合,然后枚舉所有可能的區間當成一個子集。在每個區間中把石子分成左右兩堆,K為左右兩堆的分界點,每一次枚舉k,都要更新當前區間合并石子的最小值。最終根據f數組的含義,f[1][n]即為答案。
eg3:最長公共子序列
子串要求連續,子序列只要求相對順序。
一個長度為n的序列,據每個數是在或不在這個子序列兩種情況,所以一共有2的n次方個不同的子序列。暴力枚舉一定會超時,所以用dp來做。
分析

按照最后一個不同點劃分:第一個字符串的最后一個字符a[i]是否包含在這個子序列里,第二個字符串的最后一個字b[j]是否包含在這個字序列里來劃分。a[i]和b[j]是否包含各有兩種選擇,所以一共是四種選擇。用0表示不包含,1表示包含,前面的代表a[i],后面的代表b[j],四種情況如上圖
對于11這種情況,只有a[i]=b[j]時才存在
對于01這種情況,f(i-1, j) 不一定會存在 bj,但已經考慮了含概 bj 可能中的最大值,雖然不含 ai 和 bj 已經在 00 中考慮了,這里就是重復,求最大最小值,重復考慮是沒問題的,但是求和的時候不能重復考慮。
同理,對于10這種情況,重復考慮也是沒問題。
f[i][j]含義:所有序列a[1~i]與序列b[1~j]的公共子序列的集合中,最長公共子序列的長度。
因此,f[n][m]即為最終答案。
代碼

最后
我們要相信科學,不要相信玄學。
如果上述解釋有不對的地方,歡迎大家指正





:基礎概念與架構)













