目錄
1.線性表
2.順序表
2.1概念與結構
2.2分類
2.2.1靜態順序表
2.2.2動態順序表?
3.動態順序表的實現
3.1.SeqList.h
3.2.SeqList.c
3.2.1初始化
?3.2.2銷毀
3.2.3打印
3.2.4順序表擴容?
3.2.5尾部插入及尾部刪除?
3.2.6頭部插入及頭部刪除?
3.2.7特定位置插入及刪除?
3.2.8查找元素,返回下標?
?4.順序表算法題
1.力扣:移除元素
核心思想
算法步驟
?2.力扣:刪除有序數組的重復項
核心思想
算法步驟
?3.力扣:合并兩個有序數組
核心思想
算法步驟
1.線性表
在講順序表之前,我們首先要介紹一個概念,線性表。
線性表(Linear List)是數據結構中最基礎、最常用的一種結構,它的特點是數據元素之間按線性順序排列,每個元素最多有一個前驅和一個后繼。
線性表有兩種實現方式,其一是順序表,其二是鏈表。以下我們來為他們做一個簡單區分:
| 順序表(順序存儲) | 鏈表(鏈式存儲) | |
| 實現方式 | 用數組存儲元素,內存連續分配 | 用結點存儲元素和指針,內存非連續分配 |
| 特點 |
|
|
| 適用場景 | 元素數量固定、頻繁查詢、少增刪。 | 頻繁增刪、元素數量變化大。 |
表格內容暫時看不明白沒有關系,這里只是做一個簡介,相信等你看完博客之后會有一個新的體會。
今天我們著重介紹的是順序表,鏈表會放在下一篇博客中精講。
2.順序表
2.1概念與結構
概念:順序表是??段物理地址連續的存儲單元依次存儲數據元素的線性結構,?般情況下采?數組存儲。

順序表和數組的區別??
順序表是數據結構中線性表的一種實現方式,本質是基于數組的封裝,通過數組實現元素的連續存儲,并添加了對數據操作的邏輯(如插入、刪除、擴容等)。
2.2分類
2.2.1靜態順序表
定義與特點
-
固定容量:在創建時分配固定大小的內存空間,無法動態擴展或收縮。
-
內存分配:通常在編譯階段確定(如全局數組)或在棧上分配(如局部數組),內存管理由系統自動完成。
-
操作限制:僅支持基本的讀寫操作,插入和刪除需手動移動元素,效率較低。
#define SLDataType int // 定義順序表元素類型為int(便于后期類型修改)
#define N 7 // 定義順序表容量為7(固定大小)// 靜態順序表結構體定義
typedef struct Seqlist { // 類型重命名為SLSLDataType arr[N]; // 固定大小的數組存儲元素int size; // 記錄當前有效元素個數(核心狀態標識)
} SL; // 類型重命名簡化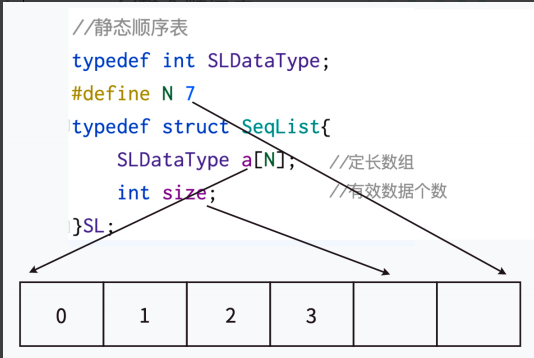
2.2.2動態順序表?
?定義與特點
-
可變容量:支持運行時動態調整容量(擴展或收縮),通過重新分配內存實現。
-
內存分配:通常在堆上動態分配,由程序邏輯管理(如?
malloc?或?new)。 -
高級操作:封裝了插入、刪除、擴容等復雜邏輯,用戶無需手動處理內存。
// 定義順序表存儲的元素類型為int
// 使用宏定義方便后續修改元素類型(例如改為float或自定義結構體)
#define SLDataType int // 動態順序表結構體定義
typedef struct Seqlist {SLDataType* arr; // 指向動態分配數組的指針(存儲元素)int size; // 當前順序表中有效元素的數量int capacity; // 當前順序表的總容量
} SL; // 使用typedef將結構體重命名為SL,簡化代碼
將靜態順序表和動態數據表做一個對比:
| 特性 | 靜態順序表 | 動態順序表 |
| 存儲方式 | 固定大小數組(棧內存/全局區) | 動態分配數組(堆內存) |
| 容量 | 編譯時確定(#define N 7),不可變 | 運行時動態調整(通過malloc/realloc) |
| 內存分配 | 自動分配和釋放(無需手動管理) | 需手動管理(malloc/free) |
| 擴容/縮容 | 不支持,大小固定 | 支持,可動態調整(如capacity不足時擴容) |
經過比對,我們發現?
靜態順序表簡單但僵化,適合確定性的小規模數據。
動態順序表復雜但強大,是現代編程語言中動態數組的基礎實現。
本文將以實現動態順序表為主,詳細講述動態順序表的擴容,頭插,尾插,刪除等操作。
3.動態順序表的實現
3.1.SeqList.h
#pragma once#include<stdio.h>
#include<stdlib.h>
#include<assert.h>typedef int SLDataType;// 動態順序表 -- 按需申請
typedef struct SeqList
{SLDataType* arr;int size; // 有效數據個數int capacity; // 空間容量
}SL;//初始化和銷毀
void SLInit(SL* ps);
void SLDestroy(SL* ps);
void SLPrint(SL* ps);//擴容
void SLCheckCapacity(SL* ps);//頭部插?刪除 / 尾部插?刪除
void SLPushBack(SL* ps, SLDataType x);
void SLPopBack(SL* ps);
void SLPushFront(SL* ps, SLDataType x);
void SLPopFront(SL* ps);//指定位置之前插?/刪除數據
void SLInsert(SL* ps, int pos, SLDataType x);
void SLErase(SL* ps, int pos);int SLFind(SL * ps, SLDataType x);
一個動態順序表至少應該能夠實現以上功能,下面我們來逐一實現。
3.2.SeqList.c
3.2.1初始化
void SLInit(SL* ps)
{ps->arr = NULL;ps->capacity = 0;ps->size = 0;
}?3.2.2銷毀
void SLDestroy(SL* ps)
{if (ps->arr){free(ps->arr);}ps->arr = NULL;ps->capacity = 0;ps->size = 0;
}注意:這里釋放空間需要判斷指針是否為空,如果是空指針直接釋放會報錯,同時我們要檢查的是ps->arr,并不是ps,需要額外注意,不要釋放ps的空間和將ps置空指針
3.2.3打印
void SLPrint(SL* ps)
{for (int i = 0; i < ps->size; i++){printf("%d ", ps->arr[i]);}printf("\n");
}3.2.4順序表擴容?
void SLCheckCapacity(SL* ps)
{// 檢查是否需要擴容(當前元素數 == 當前容量)if (ps->capacity == ps->size){// 計算新容量:如果當前容量為0(初始狀態)則設為4,否則擴容2倍int new_capacity = ps->capacity == 0 ? 4 : 2 * (ps->capacity);// 嘗試重新分配內存SLDataType* tem = realloc(ps->arr, new_capacity * sizeof(SLDataType));// 處理內存分配失敗的情況if (tem == NULL){perror("realloc"); // 打印錯誤信息exit(EXIT_FAILURE); // 終止程序(EXIT_FAILURE是標準錯誤退出碼)}// 更新順序表結構ps->arr = tem; // 指向新分配的內存ps->capacity = new_capacity; // 更新容量值}
}關鍵點說明:
擴容時機:
當
size == capacity時觸發擴容,這是為了防止下一次插入操作導致溢出擴容策略:
初始容量設為4(常見設計,避免初期頻繁擴容)
之后每次按2倍擴容(標準庫常用策略,均攤時間復雜度為O(1))
內存管理:
使用
realloc而不是malloc,可以保留原有數據必須檢查返回值是否為NULL(內存分配可能失敗)
錯誤處理:
使用
perror輸出錯誤信息(會顯示系統級的錯誤原因)
EXIT_FAILURE是標準庫定義的錯誤退出碼(通常值為1)安全性:
先將realloc結果賦給臨時變量
tem,確認成功后再賦給ps->arr避免直接
ps->arr = realloc(...)導致內存泄漏
3.2.5尾部插入及尾部刪除?
/*** @brief 在順序表尾部插入一個元素* @param ps 指向順序表結構的指針(必須非空)* @param x 要插入的元素值*/
void SLPushBack(SL* ps, SLDataType x) {assert(ps); // 確保順序表指針有效(若ps為NULL則終止程序)SLCheckCapacity(ps); // 檢查并擴容(若容量不足)ps->arr[ps->size++] = x; // 在尾部插入元素,并更新size
}/*** @brief 刪除順序表尾部元素(邏輯刪除)* @param ps 指向順序表結構的指針(必須非空且arr有效)*/
void SLPopBack(SL* ps) {assert(ps && ps->arr); // 確保順序表指針和內部數組指針均有效ps->size--; // 減少size,忽略最后一個元素(邏輯刪除)
}3.2.6頭部插入及頭部刪除?
/*** @brief 在順序表頭部插入一個元素* @param ps 指向順序表結構的指針(必須非空且內部數組已初始化)* @param x 要插入的元素值* @note 時間復雜度 O(n),需要移動所有元素*/
void SLPushFront(SL* ps, SLDataType x) {// 1. 參數校驗assert(ps && ps->arr); // 確保順序表指針和內部數組指針有效// 2. 容量檢查(必要時擴容)SLCheckCapacity(ps); // 檢查并處理容量不足的情況// 3. 移動元素:從后往前逐個后移for (int i = ps->size; i > 0; i--) {ps->arr[i] = ps->arr[i - 1]; // 將元素向后移動一位}// 4. 插入新元素到頭部ps->arr[0] = x; // 在數組頭部放入新元素// 5. 更新元素計數ps->size++; // 順序表長度+1
}/*** @brief 刪除順序表頭部元素* @param ps 指向順序表結構的指針(必須非空且順序表不為空)* @note 時間復雜度 O(n),需要移動剩余所有元素*/
void SLPopFront(SL* ps) {// 1. 參數校驗assert(ps && ps->size > 0); // 確保順序表有效且不為空// 2. 移動元素:從前往后逐個前移for (int i = 0; i < ps->size - 1; i++) {ps->arr[i] = ps->arr[i + 1]; // 將元素向前移動一位}// 3. 更新元素計數ps->size--; // 順序表長度-1/* 可選:清零最后一個元素位置的值ps->arr[ps->size] = 0; // 防止臟數據*/
}3.2.7特定位置插入及刪除?
/*** @brief 在順序表指定位置前插入元素* @param ps 指向順序表結構的指針(必須非空)* @param pos 要插入的位置索引(0 ≤ pos ≤ ps->size)* @param x 要插入的元素值* @note 時間復雜度 O(n),需要移動元素* @note 邊界情況:* - pos=0:相當于頭部插入* - pos=size:相當于尾部追加*/
void SLInsert1(SL* ps, int pos, SLDataType x) {assert(ps); // 確保順序表指針有效assert(pos >= 0 && pos <= ps->size); // 檢查位置合法性SLCheckCapacity(ps); // 檢查并擴容(若容量不足)// 從后往前移動元素,騰出pos位置for (int i = ps->size; i > pos; i--) {ps->arr[i] = ps->arr[i - 1]; // 元素后移}ps->arr[pos] = x; // 在pos位置插入新元素ps->size++; // 更新元素數量
}/*** @brief 在順序表指定位置后插入元素* @param ps 指向順序表結構的指針(必須非空)* @param pos 參考位置索引(0 ≤ pos < ps->size)* @param x 要插入的元素值* @note 時間復雜度 O(n),需要移動元素* @note 邊界情況:* - pos=0:在第一個元素后插入* - pos=size-1:相當于尾部追加*/
void SLInsert2(SL* ps, int pos, SLDataType x) {assert(ps); // 確保順序表指針有效assert(pos >= 0 && pos < ps->size); // 檢查位置合法性SLCheckCapacity(ps); // 檢查并擴容// 從后往前移動元素,騰出pos+1位置for (int i = ps->size; i > pos + 1; i--) {ps->arr[i] = ps->arr[i - 1]; // 元素后移}ps->arr[pos + 1] = x; // 在pos+1位置插入新元素ps->size++; // 更新元素數量
}/*** @brief 刪除順序表指定位置的元素* @param ps 指向順序表結構的指針(必須非空且順序表非空)* @param pos 要刪除的位置索引(0 ≤ pos < ps->size)* @note 時間復雜度 O(n),需要移動元素* @note 邊界情況:* - pos=0:刪除頭部元素* - pos=size-1:刪除尾部元素*/
void SLErase(SL* ps, SLDataType pos) {assert(ps && ps->size > 0); // 確保順序表有效且非空assert(pos >= 0 && pos < ps->size); // 檢查位置合法性// 從pos位置開始,用后續元素覆蓋當前元素for (int i = pos; i < ps->size - 1; i++) {ps->arr[i] = ps->arr[i + 1]; // 元素前移}ps->size--; // 更新元素數量/* 可選:清除殘留數據(防止臟數據)ps->arr[ps->size] = 0;*/
}3.2.8查找元素,返回下標?
/*** @brief 在順序表中查找指定元素的位置* @param ps 指向順序表結構的指針(必須非空)* @param x 要查找的元素值* @return 如果找到,返回元素的索引(0 ≤ index < size);* 如果未找到,返回 -1* @note 時間復雜度 O(n),需要遍歷數組*/
int SLFind(SL* ps, SLDataType x) {assert(ps); // 確保順序表指針有效// 遍歷順序表查找元素for (int i = 0; i < ps->size; i++) {if (ps->arr[i] == x) {return i; // 找到元素,返回索引}}return -1; // 未找到元素
}?4.順序表算法題
1.力扣:移除元素

核心思想
使用?雙指針技巧:
src(源指針):遍歷原始數組,檢查每個元素。
dst(目標指針):記錄非?val?元素的存儲位置。算法步驟
初始化?
src?和?dst?為 0。遍歷數組:
如果?
nums[src] == val:跳過該元素(src++)。如果?
nums[src] != val:將其復制到?nums[dst],然后?src++?和?dst++。最終?
dst?的值即為新數組的長度。
代碼:
int removeElement(int* nums, int numsSize, int val) {int src = 0,dst = 0;while(src<numsSize){if(nums[src]==val)src++;else{nums[dst] = nums[src];dst++;src++;}}return dst;
}?2.力扣:刪除有序數組的重復項

核心思想
使用?雙指針技巧:
dst(目標指針):記錄唯一元素的存儲位置。
src(源指針):遍歷數組,尋找與?dst?不同的元素。算法步驟
初始化?
dst = 0(第一個元素必定唯一),src = 1。遍歷數組:
如果?
nums[dst] == nums[src]:跳過重復元素(src++)。如果?
nums[dst] != nums[src]:將?nums[src]?復制到?nums[++dst],然后?src++。最終?
dst + 1?即為新數組的長度(因為索引從 0 開始)。
?代碼:
int removeDuplicates(int* nums, int numsSize) {int dst = 0,src = 1;while(src<numsSize){if(nums[dst]==nums[src]){src++;}else{nums[++dst] = nums[src++];}}return dst+1;
}?3.力扣:合并兩個有序數組

核心思想
使用?逆向雙指針法?從后向前合并,避免覆蓋?
nums1?中的未處理元素。算法步驟
初始化指針:
l1 = m - 1:指向?nums1?的最后一個有效元素。
l2 = n - 1:指向?nums2?的最后一個元素。
l3 = m + n - 1:指向?nums1?的末尾(合并后的位置)。逆向遍歷合并:
比較?
nums1[l1]?和?nums2[l2],將較大的值放入?nums1[l3],并移動對應指針。重復直到?
nums1?或?nums2?遍歷完畢。處理剩余元素:
如果?
nums2?有剩余元素(l2 >= 0),直接復制到?nums1?的前端。
代碼:
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) {int l1 = m-1,l2 = n-1,l3 = m+n-1;while(l1>=0 && l2>=0){if(nums1[l1]>nums2[l2]){nums1[l3] = nums1[l1];l3--;l1--;}else{nums1[l3] = nums2[l2];l2--;l3--;}}while(l2>=0){nums1[l3] = nums2[l2];l2--;l3--;}
}


)






)






)

