【優先算法】專題—

一、【模版】前綴和

參考代碼：

二、【模版】二維前綴和

參考代碼：

三、尋找數組的中心下標

參考代碼：

四、除自身以外數組的乘積

參考代碼：

五、和為K的子數組

參考代碼：

六、和可被K整除的子數組

參考代碼：

七、連續數組

參考代碼：

八、矩陣區域和

參考代碼：

總結

一、【模版】前綴和

【模版】前綴和

題目描述：

數組的元素是從標為1開始的，n是數組的個數，q是查詢的次數，查詢l到r這段區間的和。

解法一：暴力解法，直接查找l到r這段區間之和，但是效率太低，查詢q次每次遍歷一遍數組時間復雜度O(q*N)n和q的數據范圍是1到10^5，暴力解法過不了。

解法二：前綴和，快速求出數組中某一個連續區間的和，時間復雜度O(q)+O(N)

第一步：預處理出來一個前綴和數組，我們要要求1到3的和我們用dp[i-1]+arr[i]就是1到3的和了。

dp[i]表示：表示[1,i]區間內所有元素的和。

dp[i] = dp[i-1] + arr[i]

第二步：使用前綴和數組

如下比如我們要查找l~r這段區間的和那么我們直接去dp數組取出下標為r的這個元素，此元素就是1~r的之和我們減去l-1得到的就是l~r這段區間之和。

這里還有一個問題就是為什么下標要從1開始計數：為了處理邊界情況

初始化：添加虛擬結點（輔助結點）

參考代碼：

#include <iostream>
#include <vector>
using namespace std;int main() 
{//1.讀入數據int n,q;cin>>n>>q;vector<int>arr(n+1);for(int i = 1;i<= n;i++) cin>>arr[i];//2.預處理出來一個前綴和數組vector<long long>dp(n+1); //防止溢出for(int i = 0;i<=n;i++) dp[i] = dp[i-1] + arr[i];//3.使用前綴和數組int l,r;while(q--){cin>>l>>r;cout<<dp[r] -dp[l-1]<<endl;}}

時間復雜度：O(q)+O(n)?

二、【模版】二維前綴和

題目鏈接：二維前綴和

題目描述：

題目解析：?

1.從第一行第一列開始到第二列，到二行二列。（如下）

2.從第一行第一列開始到第三列，到三行三列。

3.從第一行第二列開始到4列，到三行四列。

算法原理：

解法一：暴力解法,模擬，讓我求哪段區間我就加到哪段區間，如下比如讓我們全部求出來那就從頭加到尾，時間復雜度高，這道題過不了因為時間復雜度為O(n*m*q)

解法二：前綴和

1.預處理出來一個前綴和矩陣

dp[i][j]表示：從[1,1]位置到[i,j]位置，這段區間里面所有元素和。

如下圖我們把它抽象出來，這里我們分為四塊面積分別為A、B、C、D，我們要求得dp[i][j]這段區間的和，我們A+B+C+D就等于dp[i][j]，我們求B和C這段區間的和是不太好求的，所以我們這樣求(A+B) + (A + C) + D - A這里減A是因為多算了一個A所以要減掉，A+B這段區間的值非常好求就是dp[i-1][j]這個位置，A+C就是dp[i][j-1]再加上D這個位置的值就是數組里面的arr[i][j]減去A也就是dp[i-1][j-1]，這樣就推出了我們預處理的公式。如下圖：

2.使用前綴和矩陣

如下假如我們要求D這段區間的和那么我們又被分成了四個部分，竟然要求D這段區間的和我們就A+B+C+D求得結果之后我們先減去上面這部分就是A+B這部分因為A+B這部分可以直接算出了，也就是下圖綠色小方塊那個位置，在減去A+C這部分但是這樣我們發現多減了一個A所以我們要加上一個A，D = A+B+C+D - (A+B)-(A+C)+A(通分之后就等于D)，A+B+C+D其實就等于dp[x2][y2]然后減去A+B也就是dp[x1 - 1][y2]再減去A+C也就是dp[x2][y1-1]在加上A也就是dp[x1-1][y1-1]，我們直接套用公式就能用O(1)的時間復雜度得出結果。

參考代碼：

#include <iostream>
#include <vector>
using namespace std;int main() 
{//1.讀入數據int n = 0,m = 0,q = 0;cin>>n>>m>>q;vector<vector<long long>>arr(n+1,vector<long long>(m+1));for(int i = 1;i <=n;i++)for(int j = 1;j <=m ;j++)cin>>arr[i][j];//2.預處理前綴和矩陣vector<vector<long long>>dp(n+1,vector<long long>(m+1));//防止溢出for(int i = 1; i<=n; i++)for(int j = 1; j<=m ;j++)dp[i][j] = dp[i-1][j] + dp[i][j-1] + arr[i][j] - dp[i-1][j-1];//3.使用前綴和矩陣int x1=0,y1=0,x2=0,y2=0;while(q--){cin>> x1 >> y1 >> x2 >>y2;cout<<dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]<<endl;}return 0;}

時間復雜為：O(n*m) + O(q)

三、尋找數組的中心下標

題目鏈接：尋找數組的中心下標

題目描述：

題目解析：?

如下圖兩邊都等于11那么就返回6的下標，如果全是0那么就返回最左邊的下標也就是0因為有多個中心下標，不存在則返回-1

解法一：暴力解法，枚舉中心下標左邊相加的值是否等于右邊相加的值，每次枚舉一次中心下標都要左邊相加右邊相加，枚舉下標時間復雜O(N)，求和依舊使用O(N)的時間復雜度，最終時間復雜度O(N^2)。

解法二：前綴和

我們利用前綴和的思想來實現，竟然要求某一段區間的和那么前綴和預處理出來的那個數組不就可以，我們還要求后面那一段區間的和我們把前綴和改一下改成后綴和就可以了。

我們用f來表示前綴和數組：f[i]表示：[0,i-1]區間，所有元素的和。

f [i]? = f [i-1] + nums[i-1]

g：后綴和數組：g[i]表示：[i+1,n-1]區間，所有元素的和

g [i] = g?[i+1] + nums[i+1]

最后進行判斷，枚舉所有的中心下標從0~n-1然后判斷f[i] == g[i]，如果有很多中心下標要返回最左邊的，所以我們枚舉所有的中心下標i，然后判斷f[i] == g[i]，因為f[i]表示的就是左邊所有元素的和g[i]保存的就是右邊所有元素的和，判斷是否相等如果相等返回i不相等繼續往后面找，找到最后一個位置依舊沒找到就返回-1

細節問題：

當我們的f等于0的時候我們代入上面發現會越界訪問，0~-1這里沒有元素所以f(0)= 0

當g等于n-1的時候我們代入上面也會發生越界訪問，n-1的右邊是沒有任何元素的所以g(0) = 0

填寫元素順序，f表是正著填的從左到右，g表是倒著填的從右到左

參考代碼：

class Solution {
public:int pivotIndex(vector<int>& nums) {int n = nums.size();vector<int>f(n),g(n);//1.預處理前綴和數組以及后綴和數組for(int i = 1;i<n;i++)f[i] = f[i-1] + nums[i-1];for(int j = n-2;j>= 0;j--)g[j] = g[j + 1] + nums[j+1];//2.使用for(int i = 0;i<n;i++){if(f[i] == g[i])return i;}return -1;}
};

時間復雜度：O(N)

四、除自身以外數組的乘積

題目鏈接：除自身以外數組的乘積

題目描述：

舉個例子：?

除1以為2*3*4等于24，除2以外1*3*4等于12，除3以為1*2*4等于8，除4以為1*2*3等于6，題目已經提示我們了使用前綴和后綴和。

解法一：暴力解法

暴力解法其實和我們上面舉的例子一樣，比如我們要求除第一個位置以外的值我們就從頭遍歷尾，要求第二個位置就從第一個開始遍歷跳過我們自己然后依次遍歷，以此類推。

但是時間復雜度太高了，O(N^2)

解法二：前綴積

本題的思路和上題的思路一樣，但是有些細節有變化。

1.預處理前綴積以及后綴積

我們不需要i位置的元素，只要0~i-1位置的元素即可。表示如下：

f：表示前綴積：f [0,i -1 ] 區間內所有元素的乘積

我們要求i-1位置的乘積的時候我們知道i-2位置的乘積讓它乘以i-1位置的值就可以了

f[i] = f [i-1] * nums[i-1]

注意：我們上面的f [i-1 ]位置是上圖i-2的位置，因為我們f[i]表示的是i-1位置。

我們知道了i+2位置的乘積之后用它乘以i+1位置的值即可。

g：表示后綴積：g[i]表示：[i+1,n-1]

g[i] = g[i+1] * nums[i+1]

2.使用

我們在i這個位置填寫數據的時候我們用f[i] * g[i]因為f[i]表示左邊的乘積g表示右邊的乘積

3.細節問題

當我們i等于0的時候，其實會越界訪問所以我們需要處理，那么我們f(0)給什么值合適上面那道題我們給的是0，這道題我們不能給0因為0*nums[i-1]還是0，那么會影響我們的結果所以我們要給1,f(0) = 1，g(n-1) = 1

參考代碼：

class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();vector<int>f(n,1),g(n,1);vector<int> answer(n);//1.預處理前綴積 后綴積for(int i = 1;i<n;i++)f[i] = f[i-1] * nums[i-1];for(int i = n-2;i>=0;i--)g[i] = g[i+1] * nums[i+1];//2.使用for(int i = 0;i<n;i++){answer[i] = f[i] * g[i];}return answer;}
};

時間復雜度：O(N)

五、和為K的子數組

題目鏈接：560. 和為 K 的子數組 - 力扣（LeetCode）

題目描述：

前綴和+哈希表

以i位置為結尾的所有的子數組在[0,i-1]區間內，有多少個前綴和等于sum[i] - k就有多少個和為k的子數組，哈希表中分別存儲前綴和、次數。

細節問題：

1.在計算i位置之前，哈希表里面只保存[0,i-1]位置的前綴和

2.不用真的創建一個前綴和數組，用一個變量sum來標記前一個位置的前綴和即可

3.如果整個前綴和等于k那么我們需要提前把hash[0] = 1。<0,1>

注意：不能使用滑動窗口來做優化(雙指針)因為有0和負數，如下圖這種情況我們left不斷向右移動，那么有可能中間還有子數組和為 k

參考代碼：

class Solution {
public:int subarraySum(vector<int>& nums, int k) {unordered_map<int,int>hash;int sum = 0,ret = 0;hash[0] = 1;for(auto x : nums){sum += x;if(hash.count(sum - k)) ret += hash[sum - k];hash[sum]++;}return ret;}
};

時間復雜度為 O(n)，空間復雜度也為 O(n)?

六、和可被K整除的子數組

題目鏈接：和可被K整除的子數組

題目描述：

補充知識：

1.同余定理：

(a - b) / p = k.....0? ? =>?a % p = b % p

舉個例子：(26-12) / 7? ?=>? ?26 % 7 = 12 % 7

7 % 2 = 1? ?-> 7 - 2 = 5 - 2 =3 -2 = 1

取余數的本質就是你這個數有多少個2的倍數就把2的倍數干掉，減到這個數比2小

(1+2 * 3) % 2 = 1(相當于有3個2的倍數，得出等式：(a + p * k) % p = a % p

證明：

(a- b) / p = k

a - b = p * k

a = b + p * k（左右相等，那么左右%p也相等）

a %p = (b + p * k) % p = b % p（p * k有k個p可以直接干掉）

2.C++，java：[負數 % 正數]的結果以及修正

負 % 正 = 負修正 a % p + p 正負統一(a %p +p) % p（如果a為正數那么就多加了一個p所以再模一個p結果是不變的，如果是負數加上一個p剛好就是正確答案）

我們使用前綴和 + 哈希表

在[0,i-1]區間內，找到有多少個前綴和的余數等于(sun % k + k)?% k，哈希表分別存儲前綴和的余數、次數

大部分邏輯和上題差不多?

參考代碼：

class Solution {
public:int subarraysDivByK(vector<int>& nums, int k) {unordered_map<int,int>hash;hash[0] = 1;//0這個數的余數int sum = 0,ret = 0;for(auto x : nums){sum += x;//算出當前位置的前綴和int r = (sum % k + k) % k;//修正后的余數if(hash.count(r)) ret +=hash[r%k];//統計結果hash[r]++;}return ret;}
};

時間復雜度為 O(n)，空間復雜度也為 O(n)?

七、連續數組

題目鏈接：連續數組

題目描述：

我們把問題轉化一下：

1.將所有的0修改為-1

2.在數組中，找出最長的子數組，使子數組中所有的元素和為0

和為k的子數組 ->和為0的子數組

前綴和 + 哈希表

1.哈希表中分別存儲前綴和、下標

2.使用完之后，丟進哈希表

3.如果有重復的<sum,i>只保留前面的那一對<sum,i>

4.默認的前綴和為0的情況hash[0] = -1，當我們的這段區間和為sum的時候我們要去0的前面也就是-1的位置找和為0的子區間(存的下標)

5.長度計算i - j + 1 - 1? ? =>? i - j

參考代碼：

class Solution {
public:int findMaxLength(vector<int>& nums) {unordered_map<int,int> hash;hash[0] = -1; //默認有一個前綴和為0的情況int sum = 0,ret = 0;for(int i = 0 ; i<nums.size();i++){sum += nums[i] == 0 ? -1 : 1;if(hash.count(sum))  ret = max(ret,i - hash[sum]);else hash[sum] = i;}return ret;}
};

八、矩陣區域和

題目鏈接：矩陣區域和

題目描述：

題目要求：以5為中心分別像上左下右分別擴展k個單位，圍城一個長方形的所有元素的和，這是假設k = 1，那么擴展一個單位。

假設求1這個位置，上左下右分別擴展1個單位，然后圍成一個正方形，最后相加即可。1+2+4+5

求2這個位置，上左下右分別擴展1個單位然后圍成正方形，相加即可，超出矩陣的范圍不需要。1+2+3+4+5+6

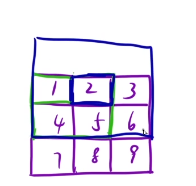
求5這個位置，上左下右分別擴展1個單位然后圍成正方形，相加即可。1+2+3+4+5+6+7+8+9

解法：使用二維前綴和

dp[i][j] = dp[i-1][j]? + dp[i][j-1] -? dp[i-1][j-1] + mat[i][j]

因為多加了一個dp[i-1][j-1]所以再減去一個dp[i-1][j-1]。

如上就是初始化前綴和矩陣的遞推公式，直接代入公式即可。

answer= dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]

這里加dp[x1-1][y1-1]是因為多減了一個dp[x1-1][y1-1]所以要加上

1.我們要求ans[i][j]位置

我們(i-k,j-k)用(x1,y2)表示

因為這個區間可能會越界，也就是說是(0,0)這個位置的時候我們不能越過，所以我們求一個最大值，如果小于0那么取最大值還是0如果大于0那么就是一個合法的區間。

x1 = max(0,i-k)

y1 = max(0,j-k)

我們(i+k,j+k)用(x2,y2)表示

我們的i+k,j+k可能會超過我們的(m-1,n-1)所以我們需要讓它回到我們的m-1,n-1

x2 = min(m-1,i+k)

y2 = min(n-1,j+k)?

2.映射位置?

當我們dp數組要填1,1這個位置的值我們要去mat數組0,0這個位置找。dp(x,y)? -> mat(x-1,y-1)。

所以我們需要把dp[i][j] = dp[i-1][j]? + dp[i][j-1] -? dp[i-1][j-1] + mat[i][j]改為dp[i][j] = dp[i-1][j]? + dp[i][j-1] -? dp[i-1][j-1] + mat[i-1][j-1]

我們在填ans數據的時候使用dp數組需要+1因為ans(0,0)對應dp(1,1)位置。(x,y)? -> (x+1,y+1)。

這里有兩種方式：

方法一：

answer[i][j] = dp[x2+1][y2+1] - dp[x1-1+1][y2+1]-dp[x2+1][y1-1+1] +dp [x1-1+1][y1-1+1];

方法二：我們在求下標那里進行+1即可，然后直接在dp數組拿值即可

x1 = max(0,i-k)+1

y1 = max(0,j-k)+1

x2 = min(m-1,i+k)+1

y2 = min(n-1,j+k)?+1

參考代碼：

class Solution {
public:vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {int m = mat.size(),n = mat[0].size();//1.預處理前綴和矩陣vector<vector<int>> dp(m+1,vector<int>(n+1));for(int i = 1;i <= m;i++)for(int j = 1;j<=n;j++)dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + mat[i-1][j-1];//2.使用vector<vector<int>> answer(m,vector<int>(n));for(int i = 0;i < m;i++){for(int j = 0;j<n;j++){int x1 = max(0,i-k) + 1,y1 = max(0,j-k)+1;int x2 = min(m-1,i+k) + 1,y2 = min(n-1,j+k)+1;answer[i][j] = dp[x2][y2] - dp[x1-1][y2]-dp[x2][y1-1] +dp [x1-1][y1-1];}}return answer;}
};