一.最大公約數

gcd(a,b)=gcd(b,a%b) 遞歸式,當且僅當b=0，易得0和a的公約數為a.(可作為遞歸的出口)

證明：

int gcd(int a, int b)
{if (b == 0) return a;else return gcd(b, a % b);
}

?二.最小公倍數

給定整數a b，求a b的最小公倍數

有圖可知

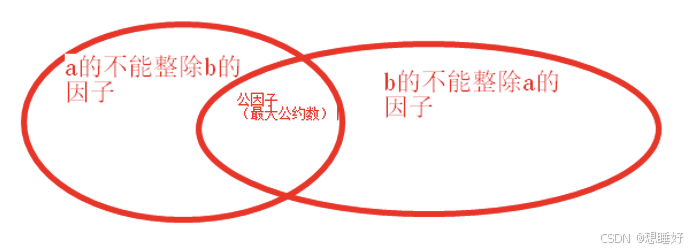
a和b 的最小公倍數等于a*b/gcd（a，b），兩個數相乘等價于a，b所有因子相乘，但中間共同部分多乘了一次，多乘的部分為a和b的最大公約數

int gcd(int a, int b)
{if (b == 0) return a;else return gcd(b, a % b);
}
int main()
{int a = 6, b = 4;//最大公約數cout << gcd(a,b)<<endl;//最小公倍數cout << a * b / gcd(a, b);
}

?

?