目錄

一、實驗目的

?二、實驗原理

三、實驗內容

四、源程序及結果

源程序（python）：

結果：

五、結果分析

---

一、實驗目的

1. 通過本實驗了解圖像的數字化過程，了解數字圖像的數據矩陣表示法。
2. 掌握取樣（象素個數）、量化與圖像質量的關系。

?二、實驗原理

????????數字化的圖像是以矩陣形式存儲的，因而數字圖像的數據矩陣表示法是指將數字化后的圖像表示為一個二維矩陣的形式，其中矩陣中的元素對應于圖像像素的灰度值。

????????對于同一幅圖像，不同的像素總數會影響其圖像的分辨率和清晰度，一般來說，越大的像素總數意味著越高的清晰度；反之，圖像的像素數越小，圖像會越不清晰，出項“棋盤格”現象（馬賽克），圖像細節越來越小。

????????不同灰度級呈現的圖像也有著類似的效果。在灰度級數量較高的情況下，圖像能夠顯示更多細微的灰度變化，這樣的圖像具有更高的對比度，黑白之間的過渡更為清晰，使得圖像更生動、細膩；相反，當灰度級數量較低時，圖像只能表示較少的灰度變化范圍，黑白之間的過渡不夠平滑，過低的灰度級還會出現“偽輪廓”現象，導致圖像中出現了不真實的邊界或輪廓。

三、實驗內容

1. 選取任意一副灰度圖像，imread進行讀取，顯示其像素值陣列。
2. 減少圖像的像素，實現多組不同像素總數表示的同一副圖像。觀察圖像采樣的像素數對圖像質量的影響，觀察“棋盤格”現象。
3. 減小同一副圖像灰度級，實現多組不同灰度級來顯示同一幅圖像，并選取合適的灰度閾值來實現一幅二值圖像。觀察圖像量化對圖像質量的影響，觀察“偽輪廓”現象。

四、源程序及結果

源程序（python）：

import cv2
from matplotlib import pyplot as pltdef pixel_list(height, width, grayscale):for i in range(height):for j in range(width):pixel_value = grayscale[i, j]print(f'{pixel_value:3}', end=' ')print('\n')if __name__ == '__main__':# 1.讀取圖片灰度圖信息img_grayscale = cv2.imread(filename='lena.jpg', flags=cv2.IMREAD_GRAYSCALE)img_height, img_width = img_grayscale.shape# 2.顯示像素陣列pixel_list(height=img_height, width=img_width, grayscale=img_grayscale)# 3.繪圖:matplot顯示圖片fig, axis = plt.subplots(2, 4)# 1）原圖axis[0, 0].imshow(img_grayscale, cmap='gray')axis[0, 0].set_title('Original(256\u00D7256)')# 2）128*128像素axis[0, 1].imshow(cv2.resize(img_grayscale, (128, 128)), cmap='gray')axis[0, 1].set_title('128\u00D7128')# 3）64*64像素axis[0, 2].imshow(cv2.resize(img_grayscale, (64, 64)), cmap='gray')axis[0, 2].set_title('64\u00D764')# 4）32*32像素axis[0, 3].imshow(cv2.resize(img_grayscale, (32, 32)), cmap='gray')axis[0, 3].set_title('32\u00D732')# 5）灰度級32img_grayscale_32 = cv2.convertScaleAbs(img_grayscale, alpha=31 / 255, beta=0)axis[1, 0].imshow(img_grayscale_32, cmap='gray', vmin=0, vmax=31)axis[1, 0].set_title('Grayscale:32')# 6）灰度級16img_grayscale_16 = cv2.convertScaleAbs(img_grayscale, alpha=15 / 255, beta=0)axis[1, 1].imshow(img_grayscale_16, cmap='gray', vmin=0, vmax=15)axis[1, 1].set_title('Grayscale:16')# 7）灰度級8img_grayscale_8 = cv2.convertScaleAbs(img_grayscale, alpha=7 / 255, beta=0)axis[1, 2].imshow(img_grayscale_8, cmap='gray', vmin=0, vmax=7)axis[1, 2].set_title('Grayscale:8')# 8）二值圖_, binary_image = cv2.threshold(img_grayscale_8, 3, 7, cv2.THRESH_BINARY)axis[1, 3].imshow(binary_image, cmap='gray')axis[1, 3].set_title('Binary Image')plt.show()

結果：

圖1 圖像像素矩陣（部分）

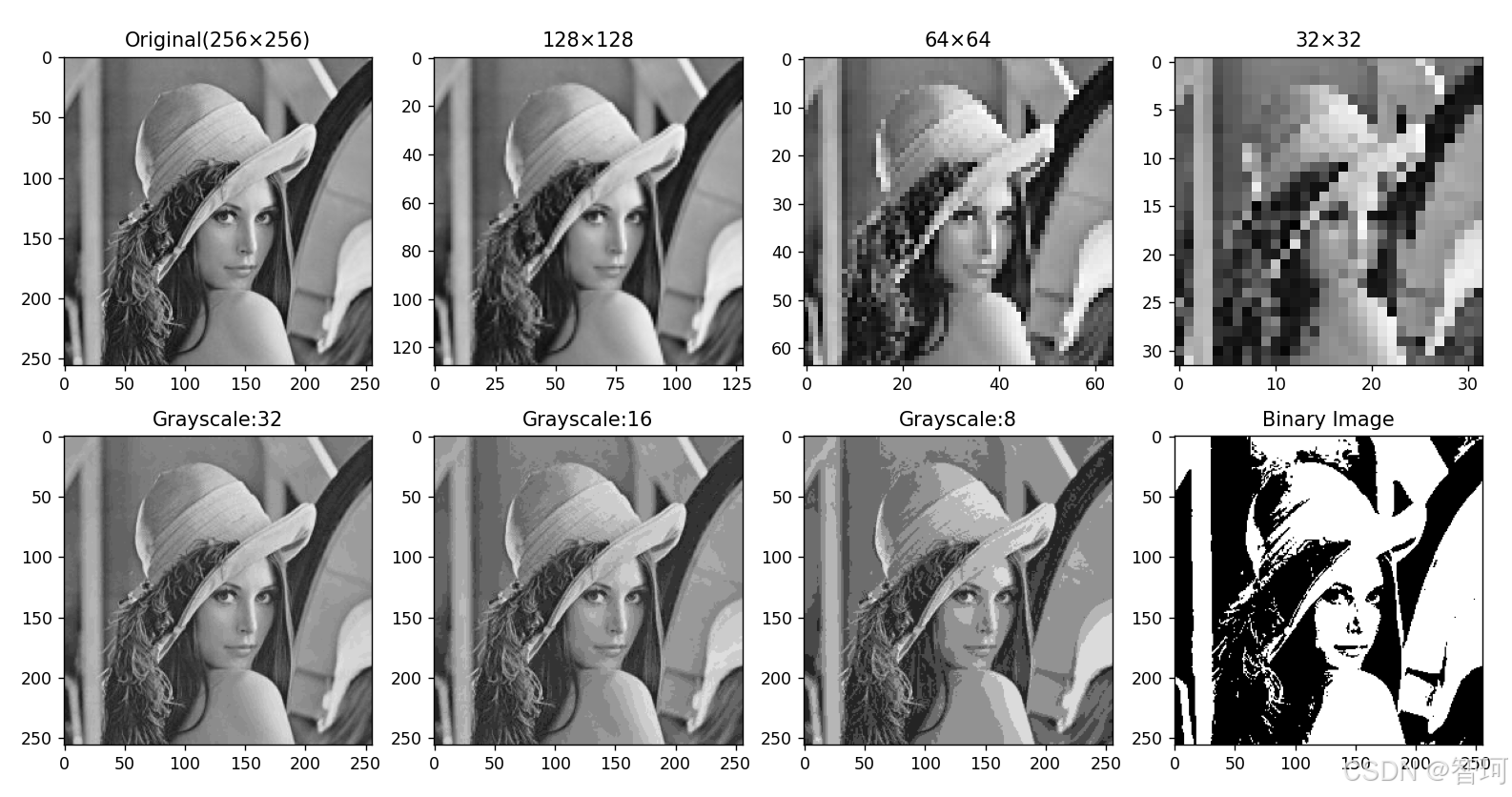
圖2 不同像素數及灰度級數下的同一圖像

五、結果分析

????????如圖一所示，一幅灰度圖像的每一個像素點都是用一個灰度級表示。實驗中使用的圖像為8比特分辨率，因此含有256個灰度級別。

????????對于不同像素數表示的同一圖像，減小像素數，在一定范圍內，圖像的變化并不明顯，如圖2中256×256和128×128圖像變化比較小，但繼續減小像素數，圖像會出現“棋盤格”現象且越來越明顯，如圖中的64×64到32×32圖像。

????????同樣的，減小灰度級數，在一定范圍內圖像的變化也不明顯，而但灰度級減小到一定程度時，便會在圖像的某些區域出現灰度突變的“偽輪廓”，而且這種現象會隨灰度級減小越來越明顯，如圖2中灰度級16和8的兩幅圖像。如果灰度級減小到為2時，就是所謂的二值圖，只有黑白兩種顏色，圖像邊界會更明顯。