這道題目看官方題解就好了，這個轉換圖論挺顯然的
證明一下為什么最后一定是
顯然練完貶值后圖只能長成這個樣子
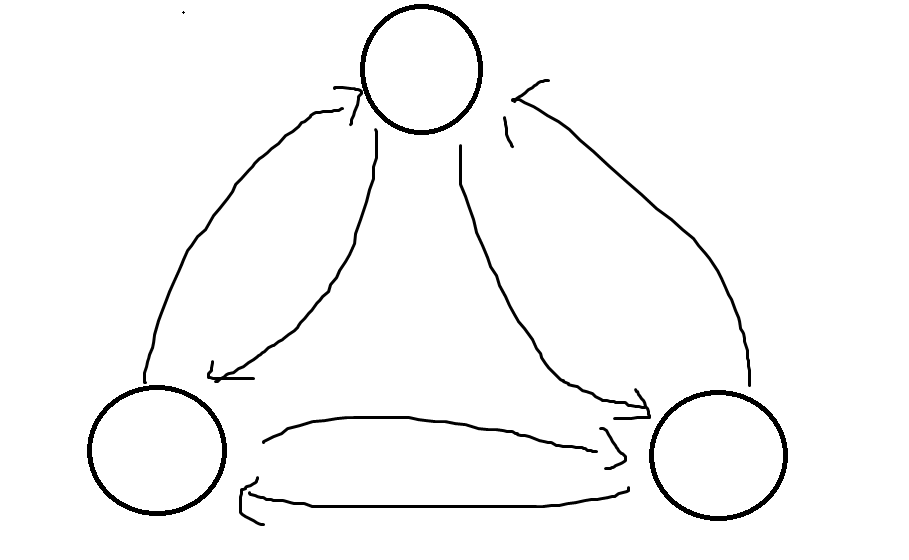
在消掉長度為\(2\)的環后，如果說圖沒邊了， 那么顯然就不用交換了，否則的話我們任取一條邊
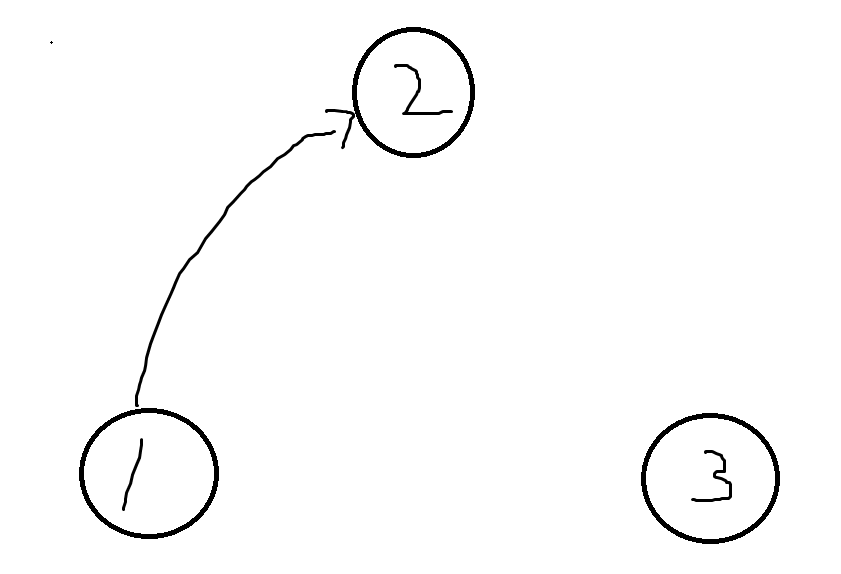
那么對于\(2\)號點來說，要么沒出邊，要么出邊的終點是\(3\)號點(因為沒有長度為\(2\)的環了)，如果說沒出邊的話，我們用抽屜原理證明矛盾：考慮\(1\)號點為什么有出邊，是因為某個字符串包含多個\(1\)，而不包含\(2\)，由抽屜原理，一定存在某一個字符串，至少包含兩個\(2\)，于是這個字符串一定會有出邊
所以只要不存在長度為\(2\)的環并且還有邊的情況下，圖只能長成這個樣子
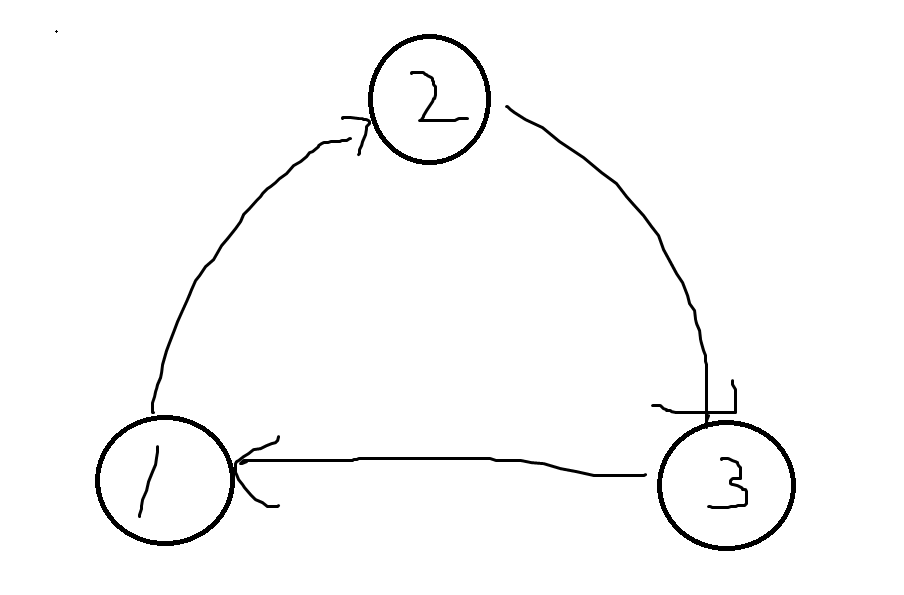
而且重邊數量一定是相等的：我們可以一直刪去一個長度為\(3\)的環，由上面“只要不存在長度為\(2\)的環并且還有邊的情況下，圖只能長成這個樣子”，不可能在某一時刻存在不是環的邊，也就是說最后一起刪完，所以說重邊數量相等
)
