文章目錄
- 📑引言
- 一、神經元和感知器
- 1.1 神經元的基本概念
- 1.2 感知器模型
- 二、多層感知器(MLP)
- 2.1 MLP的基本結構
- 2.2 激活函數的重要性
- 2.3 激活函數
- 2.4 激活函數的選擇
- 三、小結

📑引言
深度學習是現代人工智能的核心技術之一,而神經網絡是深度學習的基礎結構。神經網絡通過模擬人腦的神經元工作原理,從數據中自動提取特征并進行復雜的模式識別和分類任務。在這篇博客中,我們將詳細探討神經網絡的基本概念、構成單元、重要特性以及它們在深度學習中的關鍵作用。
一、神經元和感知器
1.1 神經元的基本概念
神經元是神經網絡的基本計算單元,其靈感來源于生物神經元。生物神經元通過接收輸入信號(來自其他神經元或感受器),經過處理后傳遞輸出信號。人工神經元模擬了這一過程,主要由以下部分組成:
- 輸入(Input): 接收來自其他神經元或輸入數據的信號。
- 權重(Weight): 每個輸入信號都與一個權重相乘,權重決定了該輸入信號的重要性。
- 加權求和(Weighted Sum): 所有輸入信號與對應權重的乘積之和。
- 激活函數(Activation Function): 將加權求和的結果轉換為輸出信號。
數學上,一個神經元的輸出可以表示為:
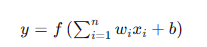
其中,( x_i ) 是輸入信號,( w_i ) 是權重,( b ) 是偏置,( f ) 是激活函數。
1.2 感知器模型
感知器(Perceptron)是最簡單的人工神經元模型,由Frank Rosenblatt在1958年提出。感知器是一種線性分類器,能夠將輸入數據分為兩個類別。其基本結構如下:
- 輸入層: 接收輸入數據,每個輸入與一個權重相乘。
- 加權求和: 將所有加權后的輸入信號相加,加上偏置。
- 激活函數: 使用階躍函數(Step Function)作為激活函數,將加權求和結果轉換為輸出。
階躍函數定義為:
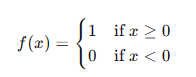
感知器模型可以表示為:
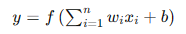
感知器的訓練過程通過調整權重和偏置,使模型能夠正確分類輸入數據。感知器的局限性在于它只能處理線性可分的數據集,對于復雜的非線性數據無能為力。
二、多層感知器(MLP)
2.1 MLP的基本結構
多層感知器(Multi-Layer Perceptron,MLP)是由多個感知器層疊組成的神經網絡模型。MLP通過引入隱藏層(Hidden Layer),能夠處理復雜的非線性數據。MLP的基本結構包括:
- 輸入層: 接收輸入數據。
- 隱藏層: 由多個神經元組成,通過激活函數進行非線性變換。
- 輸出層: 生成最終的輸出結果。
每一層的輸出作為下一層的輸入,層與層之間全連接(Fully Connected),即每個神經元與上一層的所有神經元相連。
2.2 激活函數的重要性
激活函數是MLP中引入非線性的關鍵,使得神經網絡能夠擬合復雜的非線性關系。
常見的激活函數包括:
- Sigmoid函數:
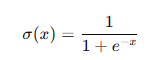
Sigmoid函數將輸入壓縮到(0, 1)之間,適用于輸出為概率的任務,但容易導致梯度消失問題。
- Tanh函數:
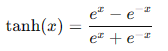
Tanh函數將輸入壓縮到(-1, 1)之間,相比Sigmoid具有零中心,但仍有梯度消失問題。
- ReLU函數(Rectified Linear Unit):
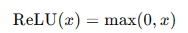
ReLU函數解決了梯度消失問題,計算簡單,廣泛應用于現代神經網絡中。但其可能導致部分神經元“死亡”,即在訓練過程中輸出恒為零。
- Leaky ReLU函數:
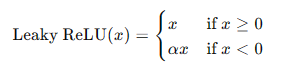
Leaky ReLU在負軸上保留一部分信息,避免了神經元死亡的問題。
MLP的訓練
MLP的訓練過程包括前向傳播(Forward Propagation)和反向傳播(Backpropagation)。前向傳播計算每層的輸出,反向傳播計算誤差梯度并更新權重。
- 前向傳播: 從輸入層開始,逐層計算輸出,直到輸出層生成最終結果。
- 反向傳播: 從輸出層開始,逐層計算誤差梯度,并使用梯度下降法更新權重和偏置。
反向傳播的關鍵是鏈式法則(Chain Rule),通過鏈式法則計算每層的梯度:
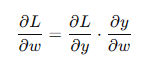
其中,( L ) 是損失函數,( y ) 是輸出,( w ) 是權重。
2.3 激活函數
激活函數的作用
激活函數在神經網絡中起到引入非線性的作用,使得神經網絡能夠學習和擬合復雜的非線性關系。不同的激活函數具有不同的特性和應用場景。
常見激活函數
- Sigmoid函數:
Sigmoid函數將輸入值映射到(0, 1)之間,常用于二分類問題的輸出層。其數學表達式為:
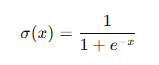
**優點:**平滑且連續,輸出范圍在(0, 1)之間。
**缺點:**容易導致梯度消失問題,訓練深層網絡時效果不佳。
- Tanh函數:
Tanh函數將輸入值映射到(-1, 1)之間,常用于隱藏層的激活函數。其數學表達式為:
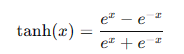
**優點:**零中心化,輸出范圍在(-1, 1)之間。
**缺點:**與Sigmoid函數類似,也容易導致梯度消失問題。
- ReLU函數:
ReLU函數是現代神經網絡中最常用的激活函數,輸出輸入值與0的較大者。其數學表達式為:
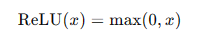
**優點:**計算簡單,能夠有效解決梯度消失問題,提高訓練速度。
**缺點:**可能導致部分神經元“死亡”,即在訓練過程中輸出恒為零。
- Leaky ReLU函數:
Leaky ReLU函數是ReLU的變種,在負軸上保留一部分信息,避免神經元死亡的問題。其數學表達式為:
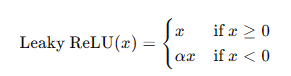
**優點:**避免神經元死亡,保留負值信息。
**缺點:**需要手動調節參數 ( \alpha )。
2.4 激活函數的選擇
激活函數的選擇對神經網絡的性能有重要影響。
一般來說,隱藏層使用ReLU或其變種(如Leaky ReLU),輸出層根據具體任務選擇Sigmoid或Tanh函數。對于回歸問題,輸出層可以直接使用線性激活函數。
三、小結
神經網絡是深度學習的基礎結構,通過模擬人腦的神經元工作原理,能夠從數據中自動提取特征并進行復雜的模式識別和分類任務。本文詳細探討了神經元和感知器、多層感知器(MLP)、激活函數的基本概念和關鍵技術。希望通過這篇詳細的博客,讀者能夠全面理解神經網絡的基礎知識,為深入學習和研究深度學習技術打下堅實的基礎。
最終篇)

)





Plan Communication Management)
)



T2 進制判斷)





