縮放變換
均勻縮放
-
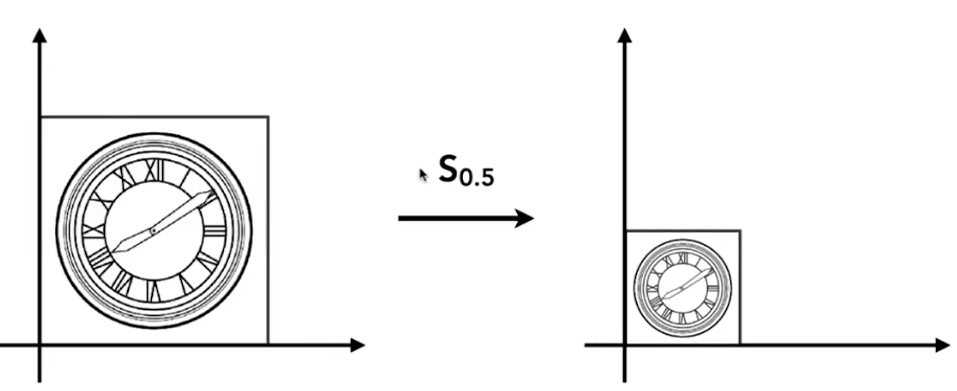
若想將一個圖形縮小0.5倍
-
若x乘上縮放值s等于x撇,y同理,則 x ′ = s x y ′ = s y \begin{aligned} & x^{\prime}=s x \\ & y^{\prime}=s y \end{aligned} ?x′=sxy′=sy?,這樣就表示了x縮小了s倍,y也是
-
將其轉為矩陣操作則是在前面乘上一個縮放矩陣 [ x ′ y ′ ] = [ s 0 0 s ] [ x y ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{ll} s & 0 \\ 0 & s \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right] [x′y′?]=[s0?0s?][xy?],根據矩陣乘法性質,其中的x撇和y撇最后乘出來就是上述的sx和sy。
-
變換矩陣為 [ s 0 0 s ] \left[\begin{array}{ll} s & 0 \\ 0 & s \end{array}\right] [s0?0s?]
非均勻縮放
- x縮放0.5倍,y不變
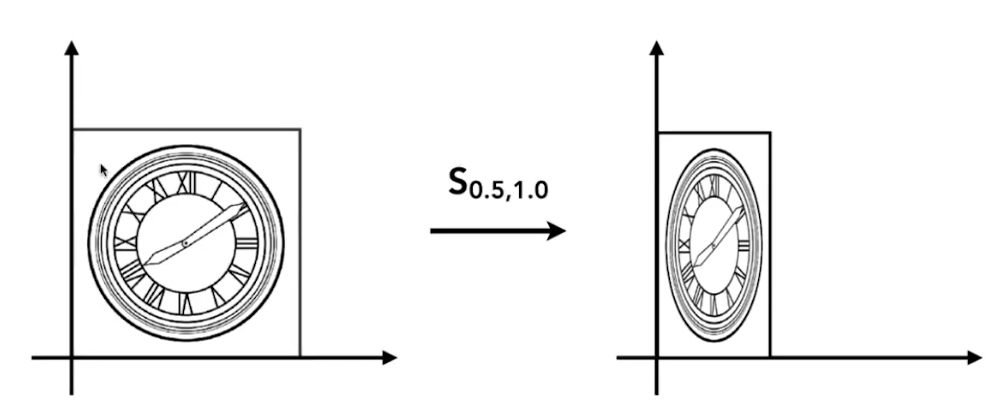
- 和上述公式一樣,只不過將對角矩陣的下面那個換一下就行 [ x ′ y ′ ] = [ s x 0 0 s y ] [ x y ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{cc} s_x & 0 \\ 0 & s_y \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right] [x′y′?]=[sx?0?0sy??][xy?]
- 其中sx為x軸的縮放倍數,sy為y軸。
- 變換矩陣為 [ s x 0 0 s y ] \left[\begin{array}{cc} s_x & 0 \\ 0 & s_y \end{array}\right] [sx?0?0sy??]
鏡像變換
- 若要將x沿x軸鏡像,則表達為 x ′ = ? x y ′ = y \begin{aligned} & x^{\prime}=-x \\ & y^{\prime}=y \end{aligned} ?x′=?xy′=y?
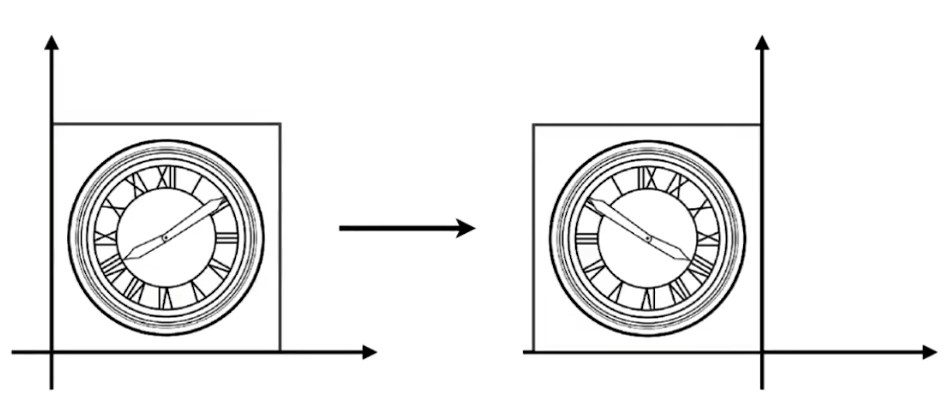
- 其矩陣形式則為 [ x ′ y ′ ] = [ ? 1 0 0 1 ] [ x y ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{cc} -1 & 0 \\ 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right] [x′y′?]=[?10?01?][xy?]
- 變換矩陣為 [ ? 1 0 0 1 ] \left[\begin{array}{cc} -1 & 0 \\ 0 & 1 \end{array}\right] [?10?01?]
剪切變換
- x軸拉長,y軸不變
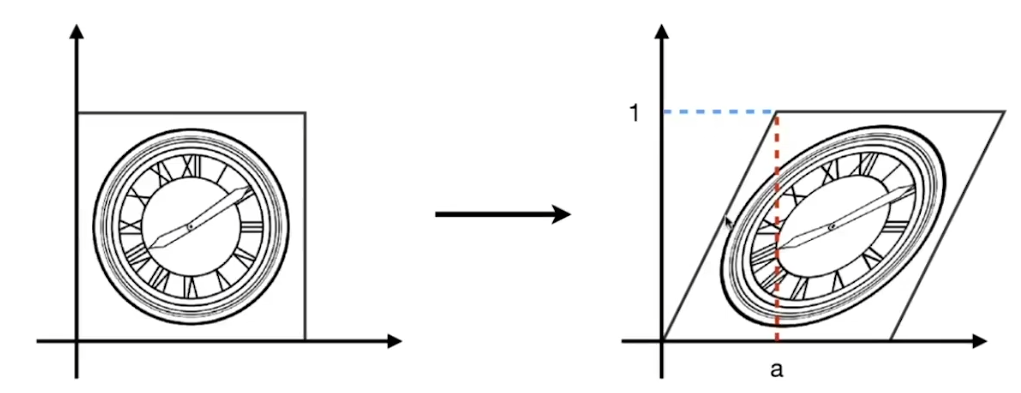
- 當y=0時,水平方向不變
- 當y=1時,水平方向向右移動a個位置
- 于是可推出,當y為1/2時,則移動后的x應該在原本的x+ay處,也就是x根據變換后為x+ay,y不變
- 用矩陣表達則為 [ x ′ y ′ ] = [ 1 a 0 1 ] [ x y ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{ll} 1 & a \\ 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right] [x′y′?]=[10?a1?][xy?]
- 變換矩陣為 [ 1 a 0 1 ] \left[\begin{array}{ll} 1 & a \\ 0 & 1 \end{array}\right] [10?a1?]
旋轉變換
- 若無特殊說明,若說A旋轉45度,則表示為A繞原點逆時針旋轉45度
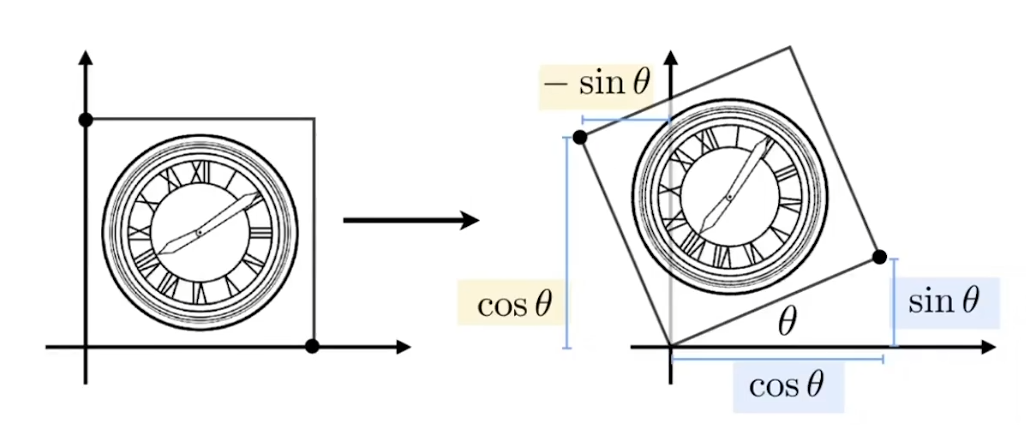
- 則旋轉矩陣為 R θ = [ cos ? θ ? sin ? θ sin ? θ cos ? θ ] \mathbf{R}_\theta=\left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right] Rθ?=[cosθsinθ??sinθcosθ?]
- 也就是 [ x ′ y ′ ] = [ cos ? θ ? sin ? θ sin ? θ cos ? θ ] [ x y ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right] [x′y′?]=[cosθsinθ??sinθcosθ?][xy?]
- 若旋轉角度為 ? θ -\theta ?θ,則旋轉矩陣為 R ? θ = [ cos ? θ sin ? θ ? sin ? θ cos ? θ ] \mathbf{R}_{-\theta}=\left[\begin{array}{cc} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right] R?θ?=[cosθ?sinθ?sinθcosθ?],其中 cos ? ( ? θ ) = cos ? ( θ ) , sin ? ( ? θ ) = ? sin ? ( θ ) \cos(-\theta)=\cos(\theta),\sin(-\theta)=-\sin(\theta) cos(?θ)=cos(θ),sin(?θ)=?sin(θ)
- 由此可觀察得到, R ? θ = R θ T \mathbf{R}_{-\theta}=\mathbf{R}_{\theta}^T R?θ?=RθT?,我們知道,旋轉 θ \theta θ角度和旋轉 ? θ -\theta ?θ角度是互逆的,也就是 R ? θ = R θ ? 1 \mathbf{R}_{-\theta}=\mathbf{R}_{\theta}^{-1} R?θ?=Rθ?1?,所以在這可以得到一個很有用的性質,即想求一個圖形旋轉 ? θ -\theta ?θ角,我們只需要計算它旋轉 θ \theta θ角度矩陣的轉置即可。
- 變換矩陣為 [ cos ? θ ? sin ? θ sin ? θ cos ? θ ] \left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right] [cosθsinθ??sinθcosθ?]
線性變換
- 經過上述變換公式,可以發現其任意一個坐標都可以通過乘上一個系數變成另一個坐標,即 x ′ = a x + b y y ′ = c x + d y \begin{aligned} & x^{\prime}=a x+b y \\ & y^{\prime}=c x+d y \end{aligned} ?x′=ax+byy′=cx+dy?
- 矩陣形式就是 [ x ′ y ′ ] = [ a b c d ] [ x y ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right] [x′y′?]=[ac?bd?][xy?],也可寫成 x ′ = M x \mathbf{x}^{\prime}=\mathbf{M} \mathbf{x} x′=Mx
- 則將這種變換取名為線性變換
平移變換
- x軸移動tx,y軸移動ty
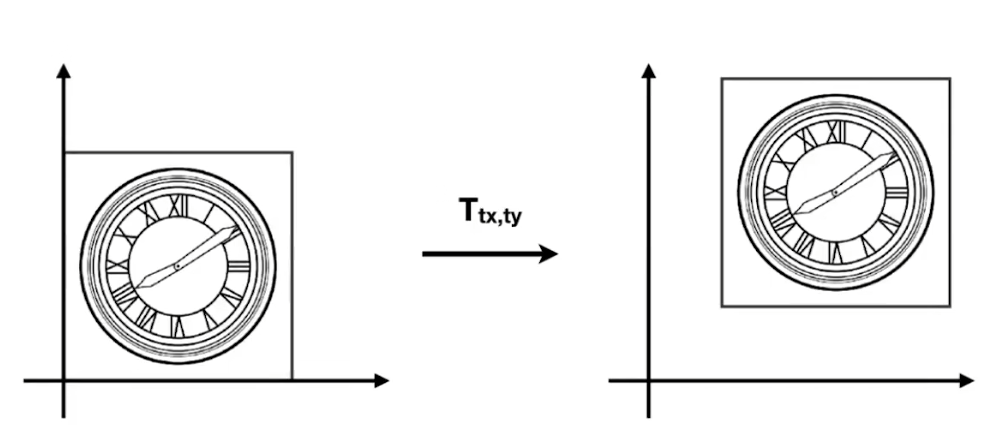
- 則在坐標上的表達為 x ′ = x + t x y ′ = y + t y \begin{aligned} & x^{\prime}=x+t_x \\ & y^{\prime}=y+t_y \end{aligned} ?x′=x+tx?y′=y+ty??
- 可是這種加法操作,并不能轉換為二維矩陣的矩陣變換,也就是乘上一個矩陣從而使得xy移動到x撇y撇
- 只能通過矩陣的加法來實現,也就是 [ x ′ y ′ ] = [ a b c d ] [ x y ] + [ t x t y ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]+\left[\begin{array}{l} t_x \\ t_y \end{array}\right] [x′y′?]=[ac?bd?][xy?]+[tx?ty??],而這種形式的變換,被稱為仿射變換
- 若不想進行其他變換,也就是旋轉啊、縮放啊等,則前面那個abcd矩陣設為單位矩陣
齊次坐標
- 為了使得在進行平移變換的時候或者其他所有的變換都只用乘一個矩陣就完成變換,所以引入了齊次坐標
- 也就是在原有維度的情況下添加了第三個坐標維度w,在原先是2d點的情況變為 ( x , y , 1 ) ? (\mathbf{x}, \mathbf{y}, 1)^{\top} (x,y,1)?
- 原先是2d向量的情況現在變為 ( x , y , 0 ) ? (\mathbf{x}, \mathbf{y}, 0)^{\top} (x,y,0)?
- 于是我們可以構建出一個矩陣,從而達成只乘一個矩陣就可完成平移變換 ( x ′ y ′ w ′ ) = ( 1 0 t x 0 1 t y 0 0 1 ) ? ( x y 1 ) = ( x + t x y + t y 1 ) \left(\begin{array}{c} x^{\prime} \\ y^{\prime} \\ w^{\prime} \end{array}\right)=\left(\begin{array}{ccc} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{array}\right) \cdot\left(\begin{array}{l} x \\ y \\ 1 \end{array}\right)=\left(\begin{array}{c} x+t_x \\ y+t_y \\ 1 \end{array}\right) ?x′y′w′? ?= ?100?010?tx?ty?1? ?? ?xy1? ?= ?x+tx?y+ty?1? ?
- 只看最右邊的前兩個值發現就是一個平移操作
- 而為啥二維的點和二維的向量要區分開呢?也就是二維點增加的維度w為1,二維向量增加的維度w為0,主要是因為向量有一個性質,就是一個向量平移到了另一個位置,那它還是那個向量,并不會發生改變
- 而看到上面的公式,若把矩陣右邊乘上的向量里的1變為0,則乘完矩陣后的值還是(x, y, 0),這樣才符合剛剛說的那個向量平移不變性的性質。
- 同時,區分點和向量還有一個好處就是,向量加向量還是一個向量,例如兩個向量相加,比如(x1, y1, 0) + (x2, y2, 0)后為(x1 + x2, y1 + y2, 0),這正好符合向量相加的原則
- 并且當兩個點相減的時候,可以理解為是從a點指向到了b點,那么這個a到b就是一個向量,也就是(x1, y1, 1) - (x2, y2, 1) = (x1 - x2, y1 - y2 , 0),這正好也符合兩個點相減的意義
- 同理可得一個點加上一個向量,就相當于該點移動了一個向量的位置到了另一個點,也就是(x1, y1, 1) + (x2, y2, 0) = (x1 + x2, y1 + y2, 1),這也正好表現為了一個點
- 所以引入齊次坐標很方便
- 而任何一個仿射變換都可以使用齊次坐標來轉換為僅需乘上一個矩陣就可完成變換
- 即 ( x ′ y ′ ) = ( a b c d ) ? ( x y ) + ( t x t y ) \binom{x^{\prime}}{y^{\prime}}=\left(\begin{array}{ll} a & b \\ c & d \end{array}\right) \cdot\binom{x}{y}+\binom{t_x}{t_y} (y′x′?)=(ac?bd?)?(yx?)+(ty?tx??)可轉換為 ( x ′ y ′ 1 ) = ( a b t x c d t y 0 0 1 ) ? ( x y 1 ) \left(\begin{array}{l} x^{\prime} \\ y^{\prime} \\ 1 \end{array}\right)=\left(\begin{array}{llc} a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1 \end{array}\right) \cdot\left(\begin{array}{l} x \\ y \\ 1 \end{array}\right) ?x′y′1? ?= ?ac0?bd0?tx?ty?1? ?? ?xy1? ?
- 也就是現在處理任何一個變換,都可以僅乘一個矩陣就可以完成變換了
- 而引入齊次坐標的上述所有變換矩陣,都可以用以下矩陣表示
- 縮放變換: S ( s x , s y ) = ( s x 0 0 0 s y 0 0 0 1 ) \mathbf{S}\left(s_x, s_y\right)=\left(\begin{array}{ccc} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{array}\right) S(sx?,sy?)= ?sx?00?0sy?0?001? ?
- 旋轉變換: R ( α ) = ( cos ? α ? sin ? α 0 sin ? α cos ? 4 α 0 0 0 1 ) \mathbf{R}(\alpha)=\left(\begin{array}{ccc} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos _4 \alpha & 0 \\ 0 & 0 & 1 \end{array}\right) R(α)= ?cosαsinα0??sinαcos4?α0?001? ?
- 平移變換: T ( t x , t y ) = ( 1 0 t x 0 1 t y 0 0 1 ) \mathbf{T}\left(t_x, t_y\right)=\left(\begin{array}{ccc} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{array}\right) T(tx?,ty?)= ?100?010?tx?ty?1? ?
- 可發現在二維仿射變換添加齊次坐標后的矩陣最后一行都是(0, 0, 1)。
逆變換
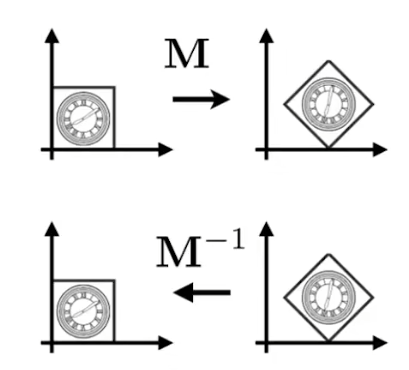
-
若A點經過一個矩陣M變換成了B點,那么則B點經過一個矩陣 M ? 1 M^{-1} M?1可重新變換成A點,這個 M ? 1 M^{-1} M?1就是逆變換矩陣
變換矩陣的合并與分解
合并
- 現在假設想將一個圖形變換為另一個圖形,如下圖所示
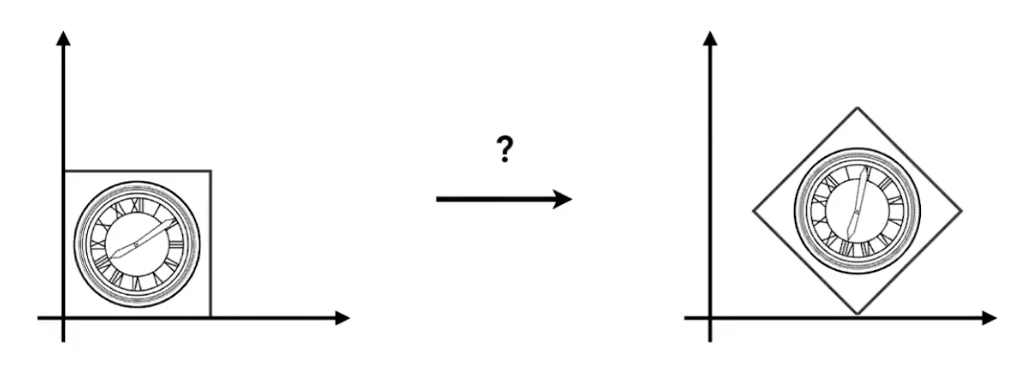
-
則明顯有一個方法,就是利用平移變換和旋轉變換
-
但是這里如果先利用平移再旋轉,則會出現下圖情況
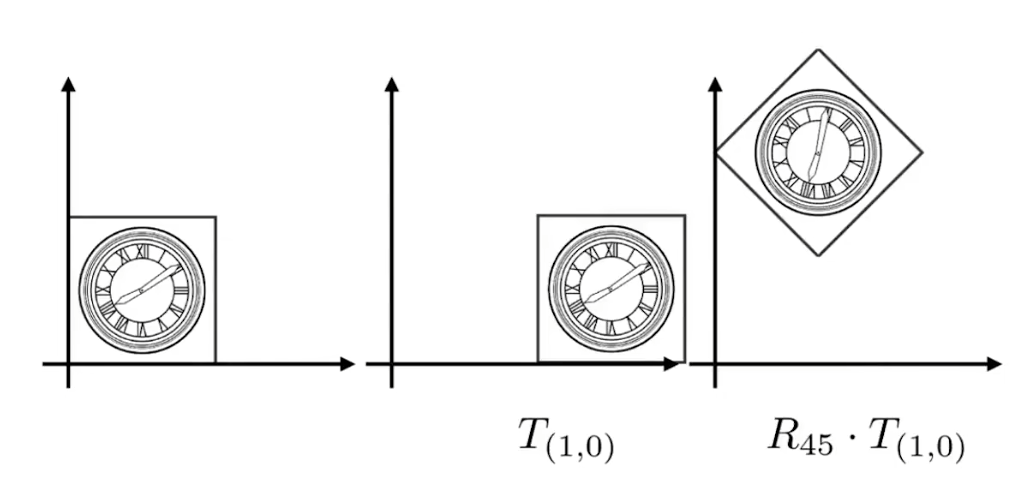
-
可以發現第一個圖形并沒有變換到我們想要的位置上
-
而如果我們先旋轉,再平移,則可以發現可以完美變換到我們想要的位置
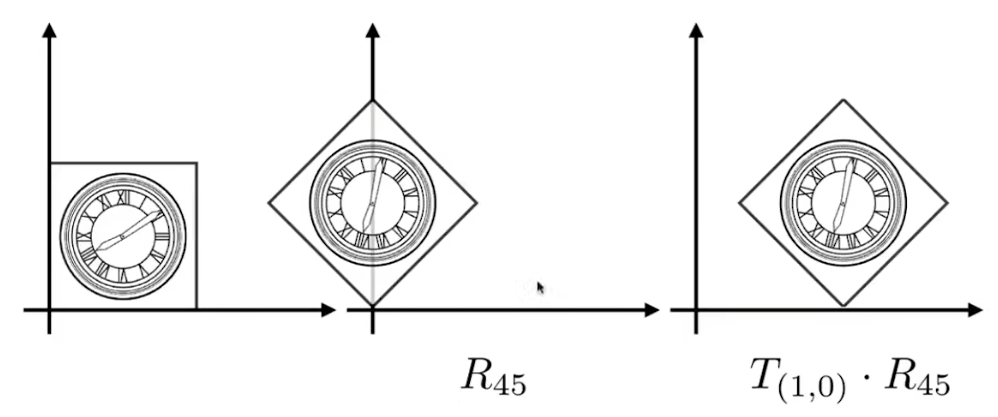
-
這說明變換的順序是非常重要的,也就是 R 45 ? T ( 1 , 0 ) ≠ T ( 1 , 0 ) ? R 45 R_{45} \cdot T_{(1,0)} \neq T_{(1,0)} \cdot R_{45} R45??T(1,0)?=T(1,0)??R45?
-
也就是我們要先將向量和旋轉矩陣相乘,再進行平移變換,即 T ( 1 , 0 ) ? R 45 [ x y 1 ] = [ 1 0 1 0 1 0 0 0 1 ] [ cos ? 4 5 ° ? sin ? 4 5 ° 0 sin ? 4 5 ° cos ? 4 5 ° 0 0 0 1 ] [ x y 1 ] T_{(1,0)} \cdot R_{45}\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right]=\left[\begin{array}{lll} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} \cos 45^{\circ} & -\sin 45^{\circ} & 0 \\ \sin 45^{\circ} & \cos 45^{\circ} & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right] T(1,0)??R45? ?xy1? ?= ?100?010?101? ? ?cos45°sin45°0??sin45°cos45°0?001? ? ?xy1? ?
-
然后我們計算順序則是要從右到左進行運算
-
而又由于矩陣有結合律,也就是(A*B)*C = A*(B*C),那么我們可以先將前面幾個變換矩陣先乘為一個矩陣,再用該矩陣去乘上向量,從而使得這個矩陣可以表示前面所有的變換操作,即 A n ( … A 2 ( A 1 ( x ) ) ) = A n ? A 2 ? A 1 ? ( x y 1 ) A_n\left(\ldots A_2\left(A_1(\mathbf{x})\right)\right)=\mathbf{A}_n \cdots \mathbf{A}_2 \cdot \mathbf{A}_1 \cdot\left(\begin{array}{l} x \\ y \\ 1 \end{array}\right) An?(…A2?(A1?(x)))=An??A2??A1?? ?xy1? ?
-
因為這些變換矩陣都是3*3的,所以當他們乘完之后的最后的矩陣也肯定還是3*3的,也就是說最后乘完的這個矩陣可以表示出非常復雜的變換
分解
-
一般情況下我們說旋轉默認都是按照原點逆時針開始旋轉,但是假設我現在想要按照當前圖形的左下角進行旋轉,應該怎么辦呢。
-
例如要將如下圖像的最左側圖形變換到最右側
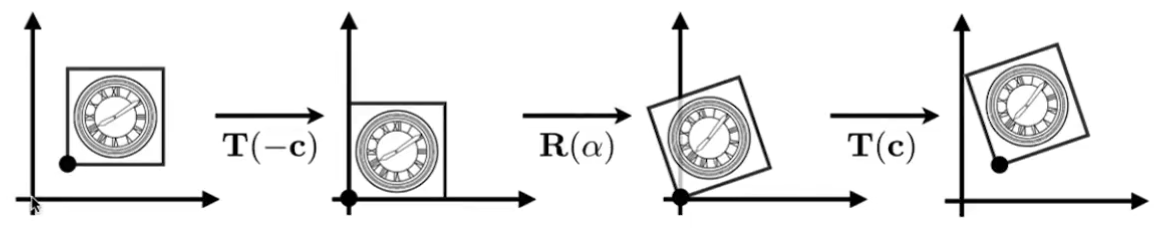
-
如果直接就旋轉變換,由于旋轉是默認對著原點旋轉的,所以就很難變成最右邊的圖形,那么我們就可以將步驟分解,先把圖形移動到原點,然后再旋轉變換,再移動回原位即可。
-
矩陣形式表達即 T ( c ) ? R ( α ) ? T ( ? c ) \mathbf{T}(\mathbf{c}) \cdot \mathbf{R}(\alpha) \cdot \mathbf{T}(-\mathbf{c}) T(c)?R(α)?T(?c)







-- 高性能可配置Echarts圖表組件封裝)





關于基礎資料/單據實體的id)

、重定義(同名隱藏)的區別 (超詳解))

)

![和Bug較勁的第n天:[Error: Unable to open snapshot file: No such file or directory]](http://pic.xiahunao.cn/和Bug較勁的第n天:[Error: Unable to open snapshot file: No such file or directory])